大型摄影棚屋盖网架与支承框架协同工作分析*

周长东， 李亚鹏， 邱意坤， 阿斯哈， 裘建东

(1 北京交通大学土木建筑工程学院，北京100044；2 中广电广播电影电视设计研究院，北京 100045)

0 引言

为满足我国文化事业的发展需求，近几年新建了多个影视基地，大量摄影棚正在建设中。大跨度空间结构具有室内无阻挡、空间大、采光充足、通风良好等优点[1-2]，与摄影棚的建筑功能要求完美契合，采用大跨空间结构形式的摄影棚结构应运而生。

现阶段，设计单位在进行上部大跨屋盖钢结构-下部混凝土支承结构的大型摄影棚混合结构体系设计时，大多将上下部结构分开，并选用不同的设计软件进行分析计算和设计[3-4]。在计算上部大跨屋盖钢结构时通常采用简化的固定支座或固定铰支座来代替下部混凝土支承结构的约束，忽略下部支承结构的水平刚度[5-6]。越来越多的研究表明，简化后的计算结果对部分杆件偏于保守，对另一部分杆件却可能偏于不安全[7-8]。

本文以某大型摄影棚结构为例，对不同边界约束条件的屋盖网架结构进行静动力对比分析，验证其上下部结构协同分析的合理性，为该类结构的优化设计提供参考。

1 工程概况

本文所选择的摄影棚位于中国某影视基地，摄影棚建筑主体为单层，周边支承结构为钢筋混凝土框架，屋盖结构为正放四角锥钢网架，纵向长度为70.8m，横向长度为40.8m，网架高度为3.2～4m，摄影棚结构基本概况见表1及表2，钢筋混凝土支承框架平面布置如图1所示。摄影棚设计使用年限50年，安全等级二级，8度抗震设防，根据《建筑抗震设计规范》(GB 50011—2010)[9]，基本地震加速度为0.3g，设计地震分组为第一组，抗震设防类别为标准设防类，场地类别为Ⅱ类，场地特征周期为0.35s。

图1 支承框架平面布置图

荷载条件：墙体线荷载取6.7kN/m；网架结构屋面荷载为：上弦恒荷载2.0kN/m2，上弦活荷载0.5kN/m2，下弦恒荷载1.5kN/m2，下弦活荷载2.5kN/m2。

下部支承框架结构构件参数 表1

网架杆件截面尺寸及数量 表2

2 计算模型的建立

为了考虑上下部结构协同工作对上部网架结构受力的影响，简化分析模型，根据实际支承情况对下部支承结构进行刚度等效[10-11]。框架梁的存在改变了框架柱沿梁边界切线方向的长细比，故将周边框架柱沿竖向和梁边界切线方向的刚度视为无穷大，只考虑沿梁边界法向的抗侧刚度[12]。据此利用SAP2000软件分别建立了屋盖网架固定铰支座模型(模型一)，等效弹性支座模型(模型二)和整体结构模型(模型三)，定义短跨方向为X向，长跨方向为Y向，竖向为Z向。其中下部支承柱、梁单元和屋盖杆件均采用SAP2000软件中的框架单元进行模拟，弹性支座采用连接单元Link进行模拟，等效弹性支座各方向的刚度如表3所示，建立的三个模型如图2所示。

图2 建立的不同支承结构模型

等效弹性支座各方向刚度/(kN/m) 表3

3 不同分析模型的静力对比

由于该屋盖网架采用的是周边支承，结构具有对称性，且结构的短跨方向是主受力方向，因此分别选择半边结构短跨方向的下弦杆(T1～T4)、腹杆(M1～M4)、上弦杆(N1～N4)作为代表杆件进行轴力对比分析，选取下弦跨中节点进行竖向位移对比分析，杆件及节点选取位置如图3～6所示。

图3 屋盖网架下弦杆T1～T4位置示意

对建立的三种模型进行静力分析，控制荷载组合取1.2恒荷载+1.4活荷载，不同计算模型在该荷载组合下得到的不同位置的杆件轴力及节点竖向位移见图7～10，其中杆件轴力受拉为正，受压为负。

图5 屋盖网架上弦杆N1～N4位置示意

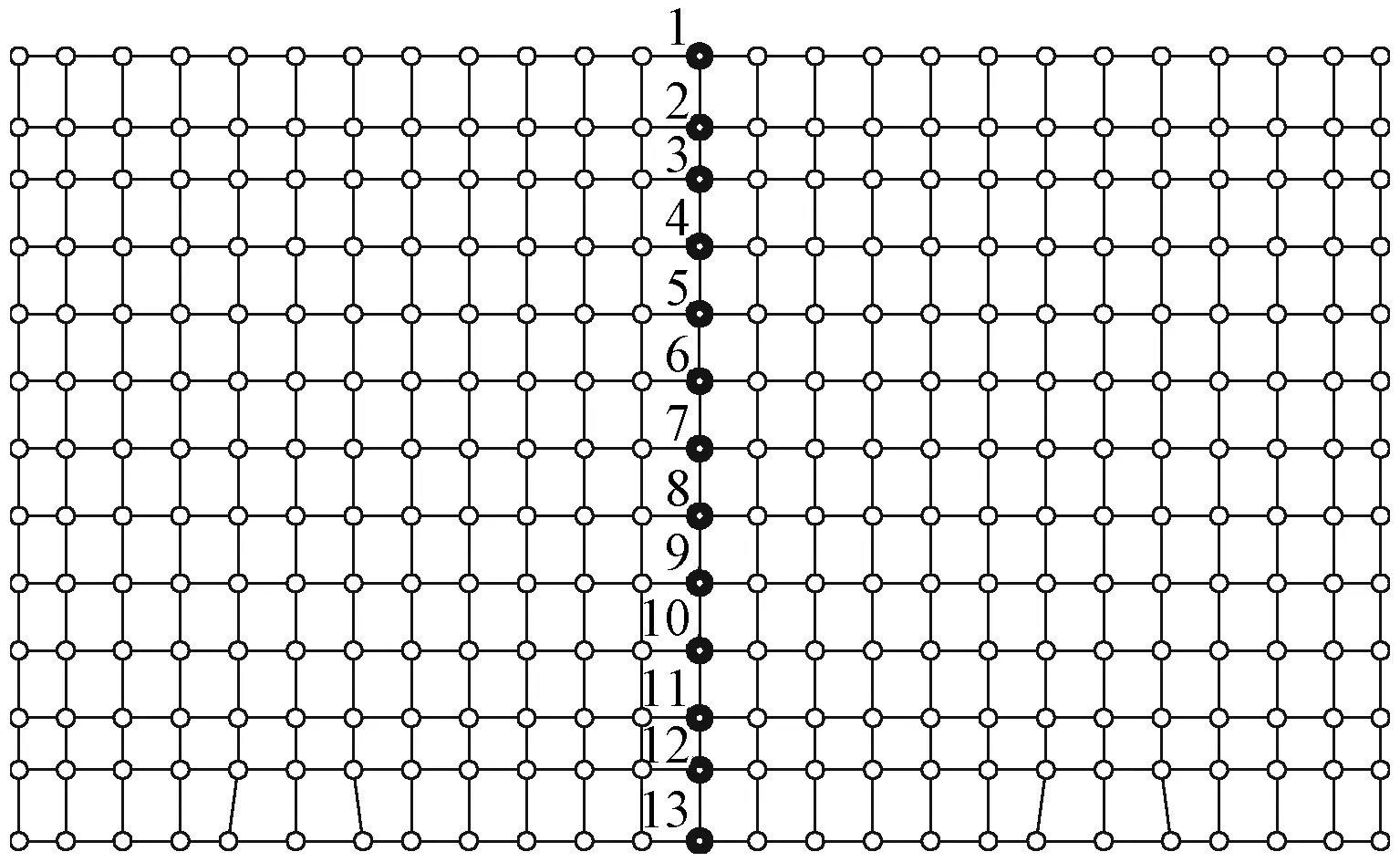
图6 屋盖网架下弦选取节点位置及编号

由图7可以看出，固定铰支座模型与整体结构模型屋盖结构的大部分杆件轴力差值较大，对于边跨下弦杆T1，固定铰支座模型与整体结构模型轴力分布相差不大，固定铰支座模型使杆件设计偏于保守；对于跨中下弦杆T2～T4，固定铰支座模型与整体结构模型内力分布严重不符，固定铰支座模型靠近支座处杆件受压，其余杆件受拉，而整体结构模型全部下弦杆受拉，杆件轴力差值最高可达307%，以T2处的6号杆件为例，杆件截面尺寸为φ180×8，模型一、模型三中的杆件轴力分别为275，579kN，若按固定铰支座模型进行设计，会使杆件极不安全。等效弹性支座模型与整体结构模型杆件受力更加接近，对于下弦杆T1，轴力差值较大，使结构设计偏于不安全，但杆件本身轴力较小，不起控制作用；对于下弦杆T2，除靠近支座处部分杆件轴力差值超过10%外，其余均在10%以内，且采用等效弹性支座模型分析内力更大，使结构设计偏于保守，仍以T2处的6号杆件为例，模型二、模型三中的杆件轴力分别为599，579kN，差值约3.5%；对于下弦杆T3和T4，所有下弦杆轴力差值均在3%以内。

图7 各模型横向下弦杆轴力对比

由图8和图9可以看出，对于腹杆和上弦杆，固定铰支座模型和等效弹性支座模型与整体结构模型轴力分布基本一致；相比固定铰支座模型，等效弹性支座模型与整体结构模型相比轴力差值大部分在10%以内，等效弹性支座模型的分析结果与整体结构模型更加接近，轴力差值较大杆件本身轴力较小，对结构不起控制作用。

图8 各模型横向腹杆轴力对比

图9 各模型横向上弦杆轴力对比

由图10可以看出，三种模型分析得到的屋盖竖向位移走势相同，固定铰支座模型的节点最大竖向位移为94.3mm，等效弹性支座的节点最大竖向位移为127.5mm，整体结构模型的节点最大竖向位移为128.3mm。固定铰支座模型的位移与整体结构模型的位移差值为26.5%，等效弹性支座模型的位移与整体结构模型的位移差值为0.62%。

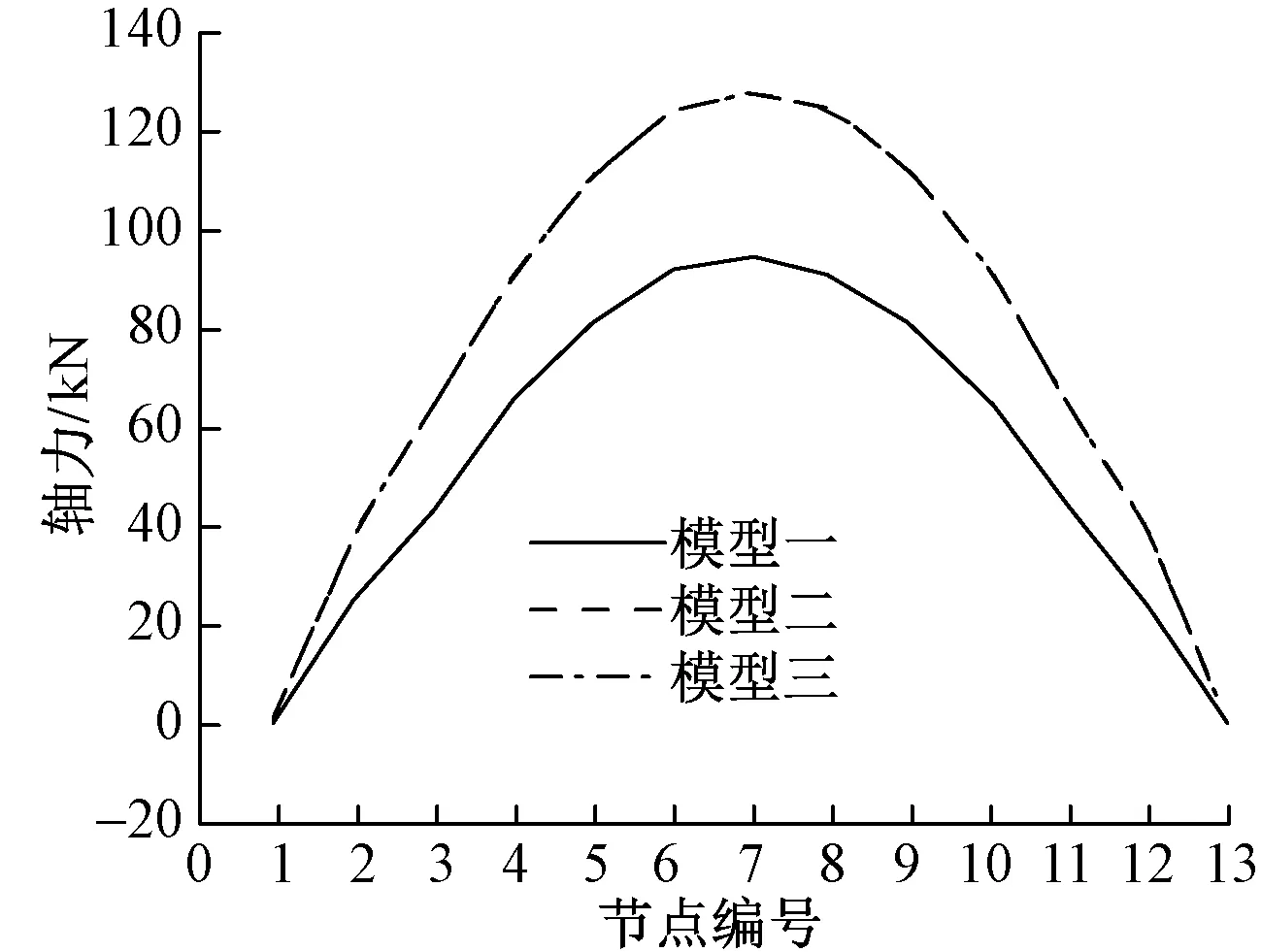
图10 各模型跨中节点竖向位移对比

总体而言，固定铰支座模型屋盖下弦杆受力与整体结构模型严重不符，其余杆件内力及节点竖向位移与整体结构模型差值较大；等效弹性支座模型和整体结构模型相比，除下弦杆支座处个别杆件轴力差值较大外，其余杆件轴力和节点竖向位移基本一致，故等效弹性支座可近似代替下部框架支承结构进行静载下结构设计与分析。

4 不同分析模型的动力对比

选取二类场地下具有代表性的El Centro波，在多遇地震下对三个模型进行单向地震作用和多向地震作用下的时程分析，单向地震时沿竖向和水平X向分别输入地震波，三向地震时加速度峰值按X向∶Y向∶Z向=1∶0.85∶0.65输入。选取跨中下弦杆T4、腹杆M4、上弦杆N4作为代表杆件进行轴力对比分析，选取跨中1～13号节点进行竖向位移对比分析。不同地震作用下各模型不同位置杆件轴力及节点竖向位移对比见图11～15(单独水平地震作用下不考虑其竖向位移)，这里只考虑了结构的地震力和动位移，轴力取地震作用下轴力绝对值的最大值。

由图11和图12可以看出，单独竖向地震作用下，固定铰支座模型下弦杆轴力分布与整体结构模型严重不符，轴力差值较大，以下弦杆T4的4号杆件为例，杆件截面为φ245×12，模型一、模型三中的杆件轴力分别为84，346kN；上弦杆轴力及跨中节点竖向位移与整体模型差值较大，以上弦杆N4的6号杆件为例，杆件截面为φ245×14，模型一、模型三中的杆件轴力分别为286，358kN，模型一、模型三中的最大节点竖向位移分别为18，30.3mm，若按固定铰支座模型进行设计，会使杆件极不安全。等效弹性支座模型与整体结构模型相比，除靠近支座两侧轴力差值较大外，其余杆件轴力及节点竖向位移基本一致，下弦杆T4的4号杆件，模型二、模型三中的杆件轴力分别为312，346kN，差值为9.9%；上弦杆N4的6号杆件，模型二、模型三中的杆件轴力分别为366，358kN，差值为2%，模型二、模型三中的最大节点竖向位移分别为29.6，30.3mm，差值为2.3%，说明竖向地震作用下有必要考虑下部支承结构水平刚度。

图11 竖向地震作用下各模型节点竖向位移对比

图12 竖向地震作用下各模型不同位置杆件轴力对比

由图13可以看出，X向水平地震作用下，固定铰支座模型所得下弦杆轴力与整体结构模型差值较大，等效弹性支座模型所得上弦杆轴力分布与整体结构模型严重不符。

图13 X向水平地震作用下各模型不同位置杆件轴力对比

由图14和图15可以看出，三向地震作用下，杆件内力分布与竖向地震作用基本一致，水平向地震会使腹杆受力增大；对于所有杆件轴力及节点位移，固定铰支座模型与整体结构模型差值均较大；由于整体结构模型更多扭转振型的参与，等效弹性支座模型得到的下弦杆轴力及腹杆轴力与整体结构模型差值也较大。

图14 三向地震作用下各模型不同位置杆件轴力对比

图15 三向地震作用下各模型节点竖向位移对比

5 不同分析模型的支座反力对比

为分析考虑上下部结构协同工作与否对下部支承框架受力的影响，需研究不同分析模型支座反力的差别。选取的支座节点编号如图16所示，由于篇幅所限，只列举了不同分析模型的静力及三维地震作用下反力对比，见图17和18，取反力绝对值的最大值进行对比分析。

图16 支座节点编号

由图17可知，静力作用下不同模型的支座反力分布如下：

图17 静力作用下各分析模型不同支座反力对比

(1)对于A1～A13支座的两个水平方向，固定铰支座模型与整体结构模型支座反力分布严重不符，固定铰支座模型跨中处支座反力最大，两侧反力最小，整体结构模型靠近角柱处的支座反力最大，跨中反力最小。这是由于结构在静力作用下使支座处产生了水平向拉力，而固定铰支座模型采用铰接约束，支座处不能产生位移，故结构对支座水平向拉力较大，从而反力较大；整体结构模型由于下部支承框架刚度有限，静力作用下支座处可产生侧向位移，释放掉大部分水平向拉力，故支座反力较小，且整体结构模型角柱附近(A2，A3支座处)的柱由于另一侧框架约束作用，柱顶位移较小，支座处位移相应减小，故水平向反力较大。对于A1～A13支座的两个水平方向，等效弹性支座模型和整体结构模型支座Y反力分布基本一致，支座X向反力分布略有差别，即角柱附近的A2，A3支座反力等效弹性支座模型较小。这是由于等效弹性支座模型只考虑了柱子本身的抗侧刚度，未考虑另一侧框架对角柱附近柱的侧向约束作用，使等效弹性支座模型在角柱附近的支座X向约束过度释放，故支座反力较整体结构模型要小。

(2)对于B1～B5支座的X向，固定铰支座模型与整体结构模型支座反力分布严重不符，固定铰支座模型跨中处支座反力最大，两侧反力最小，整体结构模型角柱处支座反力最大，跨中反力最小；等效弹性支座模型和整体结构模型支座反力分布基本一致；对于B1～B5支座的Y向，各分析模型的支座反力分布规律与A1～A13支座的X向反力分布规律一致，原因亦相同。

(3)对于A1～A13、B1～B5支座的Z向，固定铰支座模型、等效弹性支座模型与整体结构模型支座反力分布基本一致，即考虑下部支承框架与否对静力作用下支座竖向反力影响很小。

由图18可知，三向地震作用下不同模型的支座反力分布如下：

图18 三向地震作用下各分析模型不同支座反力对比

(1)对于A1～A13支座的两个水平方向，固定铰支座模型与整体结构模型支座反力分布严重不符，固定铰支座模型同一侧支座的反力基本呈左右对称分别，而整体结构模型同一侧支座的反力呈不对称分别，两侧A1～A13，a1～a13支座的反力呈镜像对称分布。这是由于固定铰支座模型采用铰接约束，约束较强，三向地震作用下，结构几乎未产生扭转；而整体结构模型在三向地震作用下，扭转较明显，故A1～A13，a1～a13支座的反力呈镜像对称分布。对于A1～A13，a1～a13支座的两个水平方向，等效弹性支座模型与整体结构模型支座反力分布基本一致，但靠近角柱处支座反力等效弹性支座模型较小，这是由于等效弹性支座模型未考虑下部支承结构质量，相对整体结构模型扭转作用较小。

(2)对于A1～A13，B1～B5支座的Z向，固定铰支座模型与整体结构模型支座反力分布严重不符，固定铰支座模型的支座反力基本呈左右对称分布，而整体结构模型的支座反力呈不对称分布，反力差值较大，这是地震作用下结构扭转所致；等效弹性支座模型与整体结构模型支座反力分布基本一致，但反力差值较大。

分析结果表明：静力作用下，固定铰支座模型主要通过跨中支座传递水平力，等效弹性支座模型和整体结构模型主要通过角柱附近支座传递水平力；三向地震作用下，相对于固定铰支座模型，等效弹性支座模型和整体结构模型角柱附近支座水平力较大。

6 结论

(1)在大型摄影棚屋盖网架结构设计与分析时，将下部框架支承结构简化为固定铰支座模型是不合理的，无论静力还是动力分析，固定铰支座模型与整体结构模型杆件轴力、节点位移和支座反力相比差值均较大，会使结构设计偏于不安全。

(2)静载和竖向地震作用下，考虑下部框架结构的水平刚度是有意义的，等效弹性支座模型与整体结构模型所得分析结果除靠近支座处杆件轴力差值超过10%外，其余杆件轴力差值很小，误差在可控范围内，且等效弹性支座模型支座反力与整体结构模型支座反力基本一致。因此只考虑静载和竖向地震作用组合时，将周边框架柱沿梁法线方向等效为弹性，沿柱的竖向和梁切线方向等效为固定可近似代替下部支承框架结构，进行结构的整体设计与分析。

(3)考虑水平向地震和三向地震作用时，由于整体结构模型有更多扭转振型的参与，等效弹性支座模型分析所得下弦杆轴力及腹杆轴力与整体结构模型差值较大，支座反力差值也较大，会使结构设计偏于不安全，应采用整体结构模型进行设计与分析。