复杂岩质边坡随机节理模拟及离散元稳定性分析
2022-01-05吴宇欣巫锡勇凌斯祥刘礼钊
吴宇欣,巫锡勇,凌斯祥,刘礼钊
(西南交通大学地球科学与环境工程学院,成都 611756)
2008年汶川地震后,震区斜坡岩土体受到很大扰动,加之地震区余震频发,汶川县地质灾害更加频繁且严重。地震导致边坡岩体节理裂隙发育,岩体强度随之降低,进而影响边坡的稳定性,岩质边坡的稳定性问题已成为影响和制约公路和铁路发展的关键技术问题之一[1]。汶川地震后震区边坡的研究成果丰富,冉涛[2]对川西交通走廊的岩质边坡失稳模式及破坏机理进行了分析,总结出典型的6种斜坡破坏-失稳模式;许强[3]对汶川诱发的大型滑坡崩塌灾害进行了研究,发现其主要具有震裂溃屈、临空抛射和碎屑流化等独特的动力学特征;牛家永[4]对地震作用下边坡的动力响应规律进行了研究,证明地震波对复杂结构面边坡的影响特征。某拟建铁路穿越汶川地震核心影响区,在调查了铁路沿线隧道进出口边坡后,发现渔子溪北岸某隧道进口岩质边坡由花岗岩组成,其岩体节理发育且空间分布复杂,具有变形破坏风险,需对其边坡稳定性进行详细研究,以保证隧道进口安全。
边坡岩体结构模型的建立很大程度上将影响其数值模拟计算[5]。陈永明[6]建立贯穿的平行节理模型,但没有考虑到岩桥以及节理接触关系对岩体强度的影响;李源亮[7]用Beacher模型对岩质节理边坡进行建模,解决的实际边坡节理离散的问题,但不能准确反映各组节理模拟程度与分布类型。蒙特卡洛法[8]是结构面网络模拟的重要方法,其根据节理的几何参数分布规律,用迹长、倾角、间距的概率分布模拟出符合实际情况的复杂节理边坡模型,可根据统计数据模拟出岩体内部无法观测的结构面网络。
目前用于研究边坡稳定性的数值模拟方法主要有流形元法(NMM)[9]、不连续变形分析法(DDA)[10]、有限元法(FEM)[11-12]、离散元法(DEM)[13-14],有限元法虽然被广泛应用,但不能考虑块体完全脱离、旋转等情况。NMM能够将岩体连续与非连续变形进行统一,但目前缺少实用高效的流形元算法。DDA可以用来模拟岩体的裂隙形变和结构的大位移、大转动,但其缺少部分材料和节理的本构关系,且DDA 通常假定整个块体为常应变块体,其应力场与坡体实际应力场不同。离散单元法常用于不连续岩体变形与稳定性分析,且适合模拟节理系统或者离散颗粒组合体在准静态或者动态下的变形过程。考虑到岩质节理边坡形变的复杂性与块体的离散性,离散元软件中 UDEC(universal distinct element code)软件[14]能准确反映坡体材料性质本构关系和节理、裂隙等性质的本构关系,能直接计算和模拟结构材料的具体破坏形式和过程,还能满足全部的平衡方程和边界条件,在实际工程中受到广泛应用。
本文的研究对象为地处地震带的汶川县某拟建铁路花岗岩边坡,为了针对花岗岩受风化、卸荷等外力地质作用产生产状不稳定、组合形式多变的复杂节理,采用蒙特卡洛随机模拟理论,通过Matlab数学分析软件,模拟岩体随机节理网络,并利用赤平投影和UDEC离散元数值模拟该边坡进行自然状态和地震作用下的稳定性及变形破坏模式分析。研究成果对该边坡的铁路建设及安全运营提供了可靠建议,蒙特卡洛随机节理网络结合UDEC数值分析的方法对地震高发地区节理发育边坡的稳定性和破坏模式研究提供了新思路和参考。
1 基本原理及方法
1.1 赤平投影法
赤平极射投影(简称赤平投影)是以球体作为投影工具,用以表示物体的几何要素或点、直线、平面的空间方向和它们之间的角距关系的一种平面投影。在岩体工程地质力学研究和实践中,用于表示岩体的结构面、岩体的滑移方向、滑动力和抗滑力等,赤平投影图常用于结构面发育岩体边坡稳定性分析。本文采用蒋爵光[15]提出的赤平投影分析方法分析边坡稳定性,该方法将坡面与结构面的关系在赤平投影上表现出来,结构面运动方向位于坡面投影外的块体有向临空面运动的趋势,反之则相对稳定。
1.2 巴顿法
为避免库伦-摩尔准则在抗剪强度计算上的误差,综合现场回弹试验,基于巴顿法(Barton)[16]对其进行简单的等效处理,得到等效的莫尔-库仑准则,最终得到等效参数C和φ:
(1)
(2)
(3)
则等效粘聚力用下面的公式表示:
Ci=τ-σn·tan(φi)
(4)
式中,JRC为结构面粗糙度系数(Joint Roughness Coefficient);JCS为结构面壁面抗压强度(Joint Compression Strength);φb为基本摩擦角;σn为结构面上的有效正应力。
1.3 蒙特卡洛法
蒙特卡洛(Monte-Carlo)法是常用的统计模拟方法和随机抽样技术,具有广泛的应用范围,是目前处理随机问题相对精确的方法。其一般思想是:通过一些抽样试验的方法,来获得随机变量或者随机事件的数字特征,从而达到求解问题的目的,其理论基础为大数定律,即在随机试验中,随着试验次数的增加,试验结果的平均值越接近于某个确定的值的规律。
2 地质特征分析
2.1 地质概况
以四川省汶川县映秀镇某拟建铁路隧道进口边坡为研究对象(图1),该边坡高约176 m,坡度为40°~60°。斜坡表面地带第四系粉质黏土、块石土覆盖层厚度较大,下部基岩为花岗岩,在拟建隧道洞口附近岩石破碎堆积,洞口所在坡面有散落岩块,G350国道穿越坡体南部。边坡为晋宁-澄江期第四期岩浆岩(γο2(4))斜长花岗岩构成,处于地震高发区,由于长期风化、卸荷等外界地质应力作用,边坡节理发育,节理产状不稳定,且组合形式多样,与常见的层状结构面边坡在地质构造方面有很大差异。通过实地调查与勘探,边坡由外及里分为强风化带、中风化带、弱风化带。根据《工程岩体分级标准》[17],边坡发育的结构面以Ⅳ类、Ⅴ类硬性结构面(节理)为主,边坡存在3组优势节理,其几何特征参数见表1。

表1 岩体结构面几何特征参数

图1 边坡岩体滑移
2.2 赤平投影分析
根据上文蒋爵光的理论分析,由实地调查边坡岩体节理数据,制作赤平投影图(图2)可知,该边坡岩体的3组节理切割岩体形成了沿单滑面滑动的滑塌体1、2、3,沿双滑面滑动的滑塌体12、13、23,及坠落体G,各个滑塌体滑动方向如图2所示。分析滑塌体稳定性,从赤平投影图中可以看出:单滑面滑塌体2、3以及双滑面滑塌体12、13、23在坡面投影之外,单滑面滑塌体2、 3的滑动方向分别为316°和324°,双滑面滑塌体12、13和23的滑动方向分别为301°、310°和243°,其中滑塌体2、3、12、13滑动方向为近坡向,所以易在边坡面上形成滑塌体。说明该斜坡易沿坡面倾向向下失稳破坏或形变。

图2 斜坡节理赤平投影图
从地震的震裂效应可知,由于斜坡的坡顶和坡面存在自由边界,没有约束,所以在地震压缩波和剪切波的作用下,被切割的岩体沿节理面错动,陡倾节理裂隙卸荷拉张,缓倾节理向临空面滑移,拉张裂隙和压剪裂隙扩展,两组节理逐渐发展形成失稳的锲形体,组成经典滑移-拉裂组合(图3)。滑移面岩石破碎程度较大,滑移过程中受到极强的拉张剪切作用,由此可以反演推测斜坡是滑移-拉裂破坏。

图3 斜坡破坏模式
3 基于蒙特卡洛法的随机节理网络模型建立
结合地质调查数据和统计资料分析结果,在边坡结构面网络模拟中,表面强风化层的Ⅳ、Ⅴ级结构面迹长和倾角的几何参数分布规律如图4~6,经过函数曲线拟合,得出J1、J2和J3的倾角和迹长概率分布类型及其均值和标准差,见表2。

表2 蒙特卡洛模拟岩体结构面几何特征参数

图4 J1倾角与迹长概率分布图

图5 J2倾角与迹长概率分布图

图6 J3倾角与迹长概率分布图
本文通过matlab实现基于蒙特卡洛法的复杂节理模拟,编程的方法如下:
(1) 确定随机结构面模型大小(长度和宽度),依据结构面间距均值以及结构面面密度公式计算出该组结构面的条数(n)。
(2) 假定模型区域结构面迹线中点服从均匀分布,由蒙特卡洛法在模型区域内均匀抽取该组结构面n条迹线的中心点坐标(xc,yc)。
(3) 确定该组结构面倾角、迹长的概率密度分布函数,同样由蒙特卡洛法随机生成对应的倾角(θ)、迹长(l)的具体随机数值。
(4) 根据中心点坐标、倾角和迹长这3个参数就可以确定一条结构面迹线。重复以上步骤即可获得某剖面的二维结构面网络图。
根据表2数据,代入matlab计算得到图7结构面网络图。

图7 Matlab随机结构面模拟
4 UDEC数值模拟分析
4.1 计算模型及参数
将上文通过Matlab创建的随机网络导入UDEC程序,并根据边坡的最易滑动面的高程数据,建立随机节理边坡数值计算模型。该模型相较于传统的贯穿节理模型,能更好地模拟出实际情况下节理的空间分布特征,使得数值模拟计算更为精确。UDEC数值模拟的模型高60 m,选取4个监测点A、B、C、D,对计算过程中斜坡的位移和速度进行监测,边坡结构面网络图模拟结果见图8。

图8 数值计算模型及监测点分布图
利用二维离散元程序UDEC对边坡模型进行数值模拟,自然工况下岩体及结构面均采用弹塑性材料,采用摩尔-库仑屈服准则,两侧边界水平方向约束,底部边界竖直方向约束;地震工况下岩体及结构面均采用弹塑性材料,采用塑性模型中的摩尔-库仑模型,两侧边界采用自由边界,底部边界采用黏滞(不反射)边界。
根据《中国地震动参数区划图》(GB 18306-2015),该边坡处于Ⅷ烈度区,本模型施加的地震加速度为正弦模拟地震波,最大幅值为0.20 g,在模型底部输入,按照比例放缩,相当于烈度为Ⅷ度的地震作用,作用时间0.1 s。模型计算中的阻尼选取为瑞利阻尼,自然频率的0.1%。
根据上文巴顿(Barton)法,取得现场岩体力学参数,结合《岩石力学参数手册》,计算得出修正后的边坡岩体力学参数,见表3,计算得出结构面力学参数,见表4。

表3 岩体物理力学参数

表4 结构面物理力学参数
4.2 计算结果分析
4.2.1 自然状态下边坡稳定性分析
自然状态下(图9),位移最大处位于斜坡顶部,位移量4.5 mm,沿竖向位移量逐渐减小,在斜坡底部达到最小值。从图中可以明显看出,在部分节理面出现位移量的较大变化,说明在节理切割岩体,节理面较岩体强度降低,易发生相对位移。从图(图10)可以看出,在计算8 000步后,最大不平衡力趋近于0,说明坡体稳定,不易发生破坏或失稳。

图9 自然状态边坡位移云图
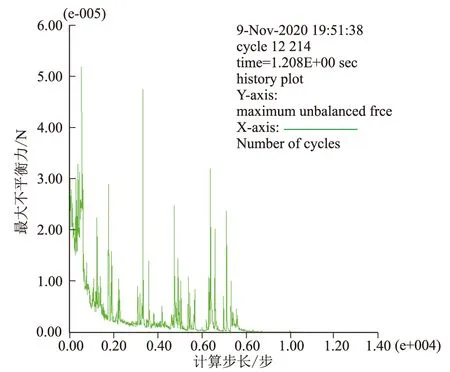
图10 自然状态边坡最大不平衡力图
从位移时程曲线(图11)可以看出,随着计算步长增大,各监测点水平和竖直方向位移增大,最终收敛,说明斜坡是稳定的。水平方向位移时程曲线显示,坡体稳定后,坡体浅表的4个监测点,从坡角到坡顶水平位移值逐渐减小,而竖直方向的位移值从坡角到坡顶水平位移值逐渐增大,说明越往坡顶竖直方向位移越大水平方向位移越小,而越向坡脚则竖直方向位移越小水平方向位移越大。该坡体顶部以竖向位移为主,坡脚处则以水平方向位移为主,符合典型的边坡滑移模式特征——坡顶竖向位移为主,坡脚水平位移为主,在坡体内部形成潜在的滑动面。
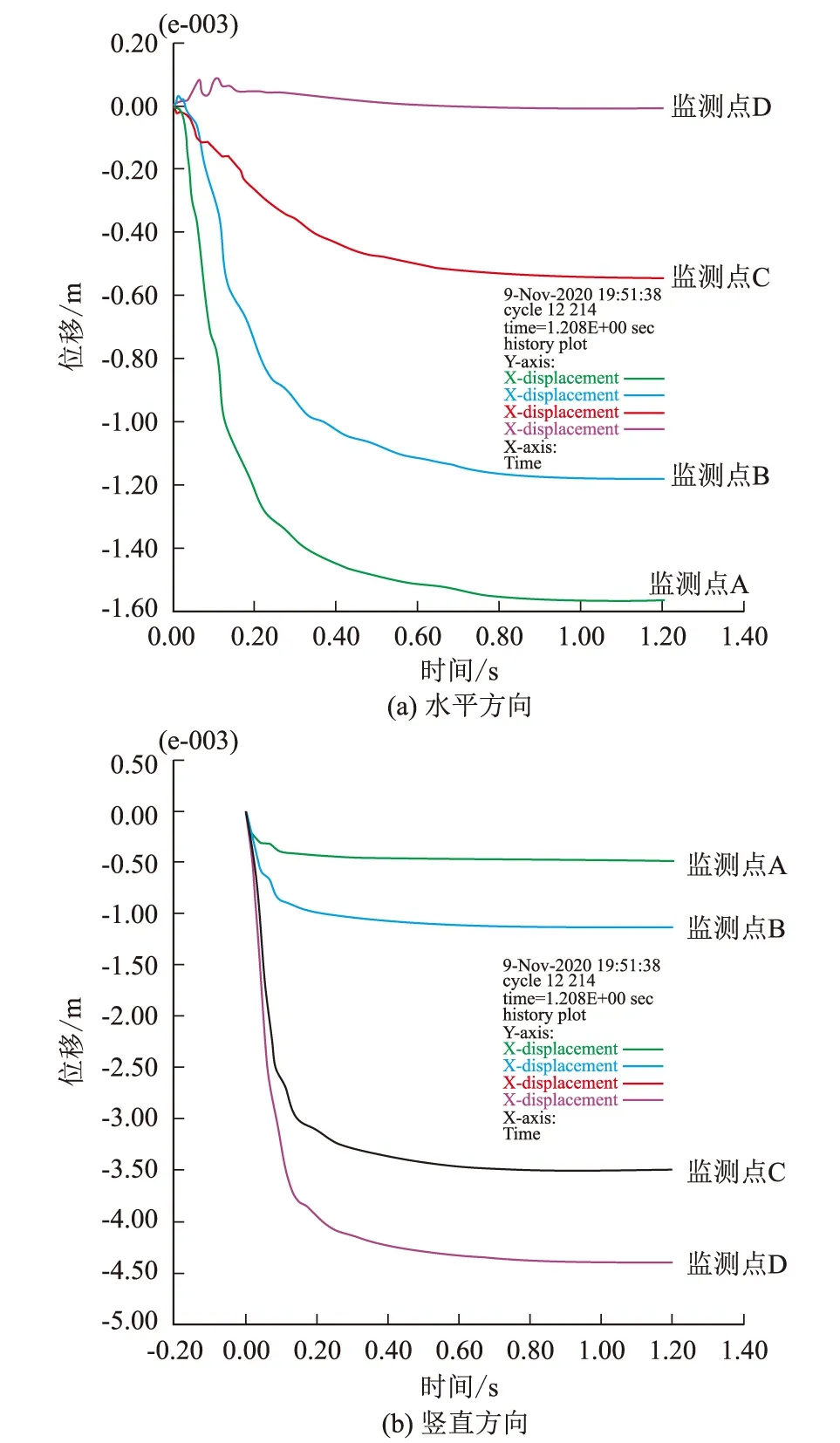
图11 自然状态下边坡监测点的位移变化
从自然状态下应力云图(图12)可以看出,(UDEC中,拉应力为正值,压应力为负值)。压应力最大值出现在斜坡底部,最小值出现在坡顶和坡面,压应力沿竖直方向逐渐增大,在自然状态下拉应力在斜坡中几乎没有出现,边坡在自然状态下整体处于受压状态,斜坡整体稳定,破坏的风险较小。

图12 自然状态下边坡应力云图
4.2.2 地震作用下边坡稳定性分析
由地震作用下边坡位移图(图13)可知,斜坡表面发生明显形变,斜坡整体沿坡面向下以及临空面运动,与节理赤平投影分析结果吻合,即节理发育的浅表层岩体向临空面卸荷滑移。斜坡表面节理发育处,岩体沿竖直方向节理张裂,并沿较水平节理滑移,最大位移达3 m。危岩体后缘拉裂,沿下缘滑移,节理对坡体破坏的影响明显,与实地调查结果(图7)相似。符合滑移-拉裂示意图(图14),后缘结构面逐渐发育,直至发生后缘拉裂破坏,后缘裂隙延伸至下部裂隙,发生滑移-拉裂破坏。从位移云图也可以看出,斜坡中部存在潜在的贯通的滑移面,在地震作用下易发生斜坡整体的滑移破坏。

图13 地震状态下边坡位移云图

图14 滑移-拉裂示意图
在地震作用后(图15),斜坡应力发生明显变化,坡体中上部出现拉应力,尤其坡顶及坡面,使得坡顶和坡面发生拉裂,在坡角出现应力集中,坡脚有向上的位移趋势,坡体中下部处于受压状态。对比自然状态下应力云图(图12),斜坡整体应力明显增大,压应力减小,拉应力增大,说明地震作用赋予坡体拉应力,使斜坡处于不稳定状态,坡面受拉沿节理发生破坏,向临空面滑移。

图15 地震作用下斜坡监测点的位移变化图
5 结论
本文结合实际调查资料,利用赤平投影和离散元数值模拟方法,对汶川县某拟建铁路斜坡在自然状态和地震作用下的稳定性及破坏模式进行分析,得出以下结论:
(1) 基于蒙特卡洛法,通过Matlab模拟随机复杂节理,能准确地模拟出节理产状在一定概率型下的模型和结构面的复杂接触关系,以及符合自然情况下节理的分布情况。
(2) 自然状况下,由赤平投影分析得出坡体有向临空面卸荷滑移的趋势,节理组成典型的滑移-拉裂破坏模式;UDEC离散元数值模拟分析得出斜坡有向临空面和向下的微小位移,但斜坡整体相对稳定。赤平投影和UDEC离散元数值模拟都分析得出自然状况下坡体易向临空面位移,但UDEC离散元数值模拟更能定量分析出位移大小,赤平投影则能从地质角度定性分析斜坡的运动趋势。
(3) 地震作用下,坡面有较大向临空面的位移趋势,与自然状态相比压应力明显减小拉应力增大,说明地震波对斜坡有拉应力作用,斜坡中部表面节理发育处破坏最严重,岩体沿竖向节理拉裂,并沿近水平向节理滑移,最终形成斜坡滑移-拉裂破坏。
