轴向移动悬臂梁振动响应及模型预测控制

陈 浩，陈继开，段应昌，贺宇锋,，罗 翔

(1.东南大学 机械工程学院，南京 211189；2.陆军工程大学 训练基地，南京 210001)

轴向运动梁问题在很多系统中都有应用，比较常见的有机械人手臂运动、火炮系统的炮管、大型卫星伸展结构以及平推式架设的军用桥梁等。其中平推式架设的桥梁车是我军目前工程保障车中的重要装备，采用平推式架设方法，可以实现大跨度的障碍架设。在架设过程中，通过配备多组滑轮进行桥梁支撑，并采用销齿传动推动桥梁轴向架设。但由于桥梁跨度较大，在架设过程中常出现振动问题，长时间的振动会严重影响架桥车的使用寿命，同时也会对架桥作业带来安全隐患。从结构上看，平推式架桥结构是一种典型的轴向运动梁系统，而轴向运动梁的动力学相应及振动控制问题一直是国内外的研究热点。李山虎等[1]通过多尺度法推导了伸展悬臂梁的独立模态振动控制的近似理论解；刘宁等[2]研究了在移动质量作用下的轴向运动悬臂梁的振动问题，并采用修正的Galerkin法对振动方程进行离散并求解。Michaltsos[3]对不同移动速度的质量载荷影响下的桥梁振动响应进行了研究；华洪良等[4]采用Rayleigh-Ritz法推导了轴向移动悬臂梁的时变动力学方程，提高数值计算效率。上述等人的研究内容集中在对不同工况下轴向移动悬臂梁的动力学响应上。

Wang等[5-6]对轴向移动梁的横向振动抑制问题进行研究;Zhu等[7]从能量角度采用边界控制策略来抑制轴向移动梁或弦的振动；王亮等[8]采用LQR(linear quadratic regulator)法设计了主动振子和主动力控制器，通过数值计算比较两种振动控制效果。张伟等[9]采用自适应控制方法对轴向运动弦和作动器组成的系统进行横向振动控制，振动抑制效果明显。刘定强等[10]采用二次最优控制和速度反馈法对轴向运动矩形薄膜横向振动的控制问题进行分析。

本文以平推式架桥车为研究对象，首先基于欧拉梁理论，采用拉格朗日法建立系统运动方程，通过以幂级数函数为基函数来构造试函数的假设模态法进行动力学求解，并对架设过程的振动响应进行参数化分析，为实际架桥车的作业和保养提供指导。然后针对架设过程的可能出现振动不确定干扰问题，拟采用一种模型预测控制的思想进行主动抑振分析。模型预测控制的核心思想是模型预测-反馈校正-滚动优化，基于模型预测控制进行主动力控制可以有效抑制不确定干扰因素影响下的振动。

1 架桥车桥梁动力学模型

架桥车装备的架设机构是采用销齿传动机构，桥梁内俩侧安装有连续排列的销轴，然后在支撑桥梁的机构上有一个用于主动驱动的齿轮，因此整个架设过程可以简化为一个简谐作用力激励下的轴向移动悬臂梁系统，如图1所示。

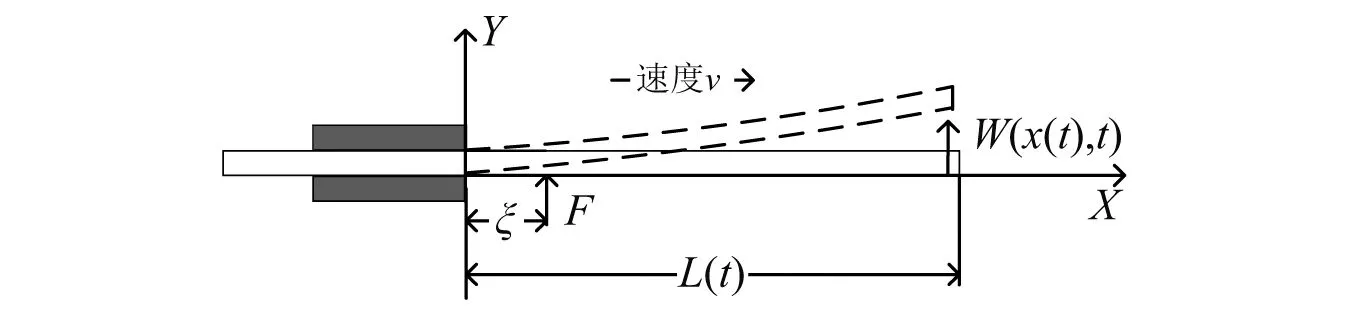
图1 轴向移动悬臂梁模型

图1中，以桥梁固定端为原点建立直角坐标系，外伸桥梁长度为L(t)，桥梁以速度v向前推出，齿轮对桥梁的激励力为F，激励力作用位置距离原点为ξ，桥梁的横向位移用为w(x(t),t)表示，桥梁的弹性模量、密度、横截面积与惯性矩分别为E，ρ，A，I。

在推桥过程中，梁上任意一点的坐标可以表示为

X=[x(t),w(x(t),t)],x∈(0,L(t))

(1)

则梁上任意一点的速度矢量由坐标矢量对时间求导可得

(2)

因此，系统的动能表达式为

(3)

式中：(·)为对时间的导数；()′为对x求导。

而梁的势能可以表示为

(4)

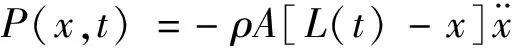
考虑整个系统的结构阻尼作用，定义梁的耗散函数为

(5)

式中，c=2mδiωi,δi为各阶模态阻尼比，ωi为各阶模态频率。

由式(3)、式(4)、式(5)，可得到轴向运动梁的拉格朗日函数

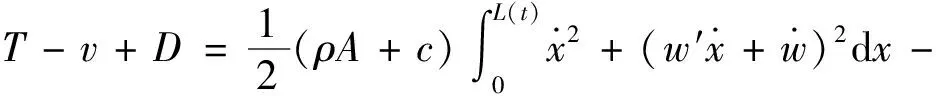
(6)

2 桥梁的横向振动方程

通过能量法求出桥梁运动系统的拉格朗日函数，对其离散化后即可推导出动力学振动方程。假设模态法是利用有限个已知的模态函数来确定系统的运动响应，因此本文通过假设模态法对系统的拉格朗日函数进行离散化处理，一般在静止悬臂梁系统中，梁的模态函数表示为

式中,λi=βiL为特征方程cosλichλi+1=0的根。根据特征方程的解可以得到桥梁的固有频率，桥跨的固有频率ω和λ的关系如式(8)所示。式(8)表明桥梁各阶模态频率与桥梁长度成反比。

(8)

由式(7)可知，悬臂梁的模态函数由一系列的三角函数和双曲函数组成，形式比较复杂，计算起来十分不易。根据文献中的拟合原则，本文采用5阶幂级数函数来拟合静止梁的模态函数，与悬臂梁的模态函数相比，幂级数的计算推导相对简单，提高了动力学建模效率。然而对于时变系统，悬臂梁的固有模态函数是没有意义的，因此取悬臂梁的瞬时模态函数作为拟合对象，梁竖直方向的振动位移w可以表示为

(9)

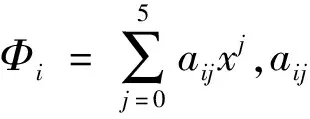
由于物体的前三阶模态一般最易被激发，所以本文以下采用三阶模态截断并将式(9)表示成矩阵的形式

w=Φ(δ)q(t)

(10)

式中：Φ(δ)=[φ1φ2φ3];q(t)=[q1(t)q2(t)q3(t)]T。将式(10)代入式(6)中，并通过拉格朗日方程可推导得到轴向移动桥梁的系统运动方程

(11)

式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;Q为广义力向量，具体的表达式为

M=m1

(12)

(13)

(14)

(15)

(16)

从上述表达式可知，由于桥梁轴向移动的影响，梁的质量矩阵、阻尼矩阵以及刚度矩阵都是时变参数，所以轴向移动梁的振动方程是一个二阶时变方程。同时，本文在推导桥梁动力学方程时忽略桥梁的结构阻尼，而式(13)阻尼项C中除了由于桥跨结构阻尼产生的c3，其余部分是由于桥跨的轴向运动以及弯曲变形引起的，也因此不能通过模态叠加的原理将多自由度的振动方程解耦成单自由度方程，这样就难以直接求出式(11)的精确解析解。所以本文采用求解精度较高的Newmark-β数值法计算振动方程的动力学响应。

3 基于Newmark法的模型预测控制

本文的研究对象始终处于轴向运动状态，从而使系统的质量参数、刚度参数以及阻尼参数都随时间变化，使用较广泛的PID(proportion intergration differentiation)控制在这种含有时变参数的系统中难以实现全局稳定[11]。针对本文系统时变特性，考虑通过模型预测控制的思想将系统全局最优问题分解成有限时间局部最优进行滚动求解。在有限时域内通过Newmark法对模型输出进行预测，根据预测时域的输出进行优化控制得到当前时刻的最优控制力，并随着时间的推进，不断进行局部最优求解从而实现全局的振动抑制控制。即通过预测模型-反馈校正-滚动优化三部分进行振动控制。

考虑在距离桥梁固定端的某位置施加横向控制力，根据实时振动输出对控制力进行调整达到抑制桥梁振动目的。在不考虑外界扰动情况下，式(11)可写成以下形式

(17)

式中,U为控制力向量。

根据Newmark-β法的假设[12]可以得到

(18)

式中，β和γ为按积分的精度和稳定性要求进行调整的参数。本文取β=0.5，γ=0.25，此时计算结果是无条件稳定的。由式(18)可解得

对动力学方程离散化，考虑t+Δt时刻的振动方程为

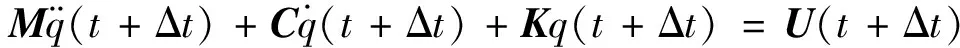
(20)

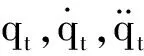
(21)

其中，

(22)

(23)

(24)

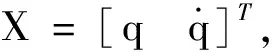
(25)

其中,

(26)

(27)

结构t时刻的加速度向量可以通过求解t时刻的离散动力学方程得到

(28)

所以式(25)可以转为

Xt+Δt=dt+ΔtXt+mt+ΔtUt+nt+ΔtUt+Δt

(29)

其中,

(30)

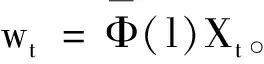
定义目标函数

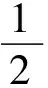
(32)

式中:w(t)=[w(t+Δt)/t…w(t+NΔt)/t]T，w(t+NΔt)/t为以t时刻状态预测的N个采样时刻后的输出；wr(t)为期望轨迹，本文中取为0；Q为N×N阶响应权矩阵；R为(N+1)×(N+1)阶控制权矩阵；N为预测步数;Δt为时间步长，显然这两个参数的取值将影响模型预测的精度。

已知每个采样t时刻的状态根据式(29)可预测出未来N个时刻的响应值w(t)，以式(32)的优化函数对未来N个时刻的预测响应值进行最优计算，得到未来N个时刻的最优控制序列U(t)，取控制序列的第一个最优控制力作用在当前时刻。在t+Δt时刻，系统将根据当前时刻的系统实际响应值重新预测未来N个时刻的系统响应，并重复进行上述最优控制计算过程。采样开始系统每次滚动一个采样步长，并在每个采样时刻都会根据当前实际响应值预测未来时刻的响应值进行最优控制，从而实现全局的最优控制。

4 数值计算及仿真分析

4.1 架设参数分析

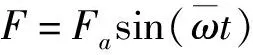
根据实际架桥车的参数，本文设置梁的初始长度为2 m，架设过程中桥梁推送长度为12 m，激励力作用点距离固定端ξ=0.925 m，等效梁的宽度b=0.234 m，厚度h=0.6 m，密度ρ=3 233.6 kg/m3，弹性模量E=2.06×1011Pa，销齿间距d=0.06 m，前三阶阻尼比均为0.014，激励力幅值为200 kN，时间步长Δt=0.02 s。

实际桥梁稳定推送速度在0.6～1.0 m/s，分别以0.6 m/s和1.0 m/s的速度推送桥梁至14 m过程中桥梁末端振动情况，如图2～图5所示。

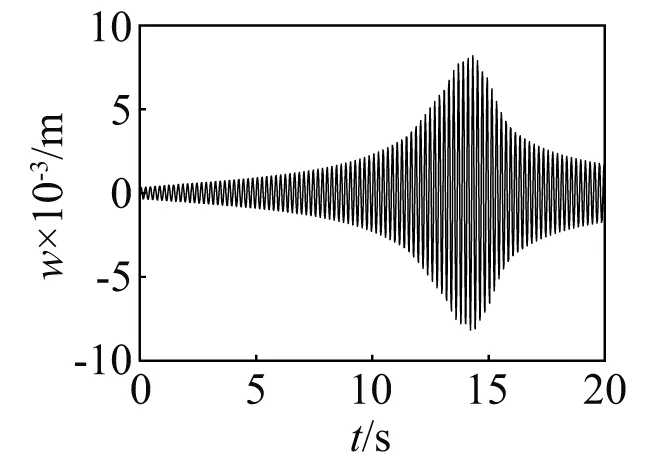
图2 v=0.6 m/s桥梁末端位移

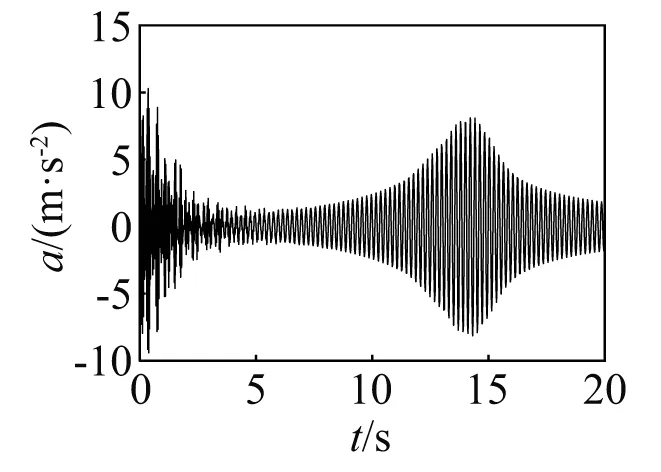
图3 v=0.6 m/s桥梁末端加速度

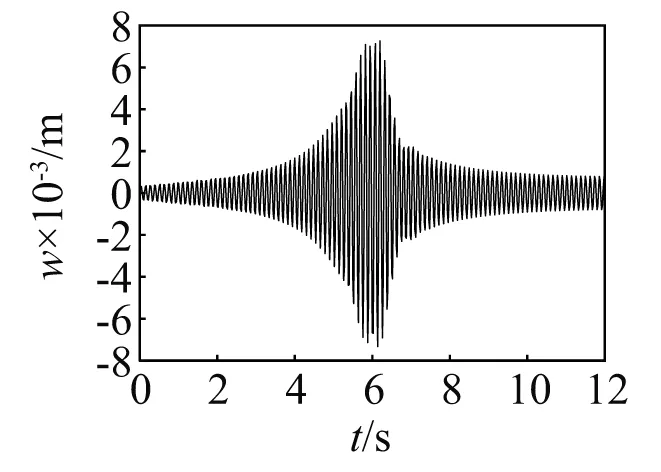
图4 v=1.0 m/s桥梁末端位移

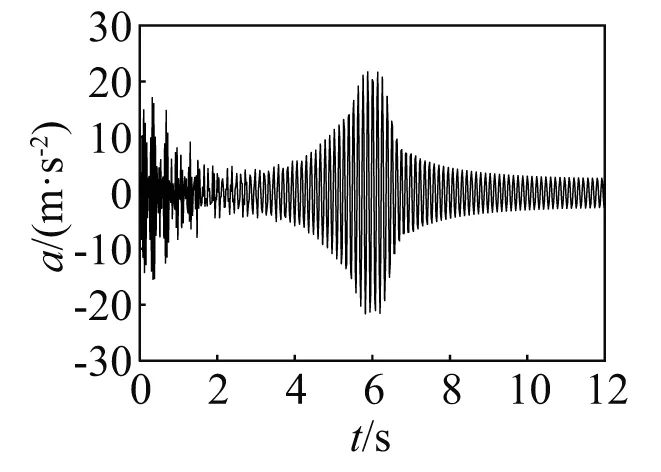
图5 v=1.0 m/s桥梁末端加速度

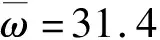
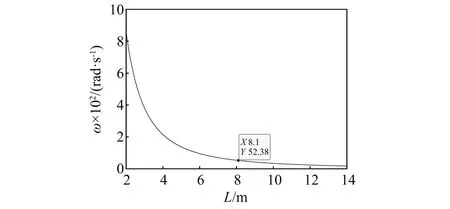
图6 一阶模态频率变化

从图6可知，在推桥初始阶段，由于桥梁长度较短，使最易激发的一阶模态频率也相对较高，因此在初始阶段应尽快将推桥速度提升至最高速度1.0 m/s；随着梁长的增加，激励力频率会慢慢接近桥梁的一阶模态频率，为了尽可能避免共振出现，在推桥长度至8 m时会和最高推桥速度下的激励力产生共振，应开始逐渐降低推桥速度以降低激励力频率来避免共振。但是由于推桥最低速度的要求，激励力频率不可避免的会接近桥梁各阶模态频率而发生共振，因此为了能够高效率架桥的同时尽量减少振动，有必要对桥梁进行主动振动抑制。

4.2 模型预测控制分析

权系数矩阵分别设为Q=6×1012×IN×N,R=I3(N+1)×3(N+1)。其他相关仿真参数如表1所示。

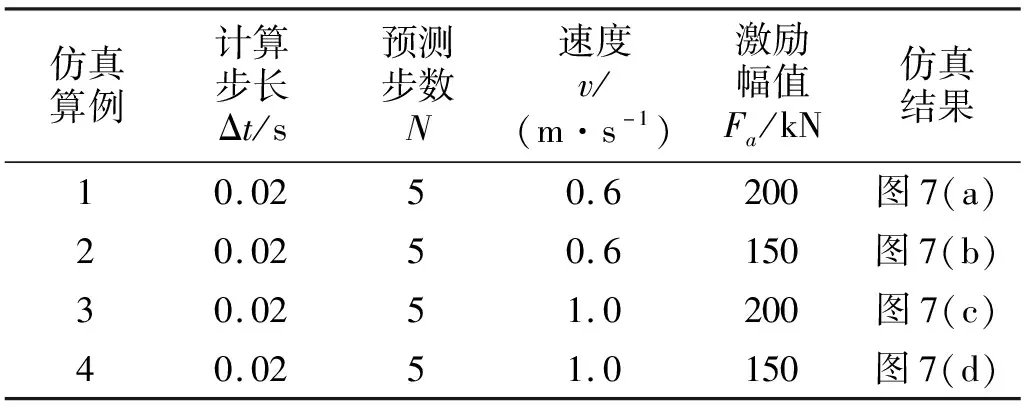
表1 相关仿真参数

分别对比图7(a)、图7(b)可知，在桥梁受到不同大小的扰动力时，基于模型预测的控制算法都可以将共振区的最大峰值减少约55.9%，同时当桥梁离开共振区后，能够在2 s内迅速衰减至稳定。而当推桥速度发生变化后，桥梁共振区域也相对发生变化，从图7(a)和图7(c)的对比可知，推桥速度也略微影响了振动控制的效果，振动抑制比下降到31%，但是由于高速架桥发生共振较早，整体的振动幅值就相对较小，因此总体控制效果还是比较明显。以上对比验证了模型预测控制策略具有较好的鲁棒性，在外界不同的干扰情况下都能够取得不错的控制效果。

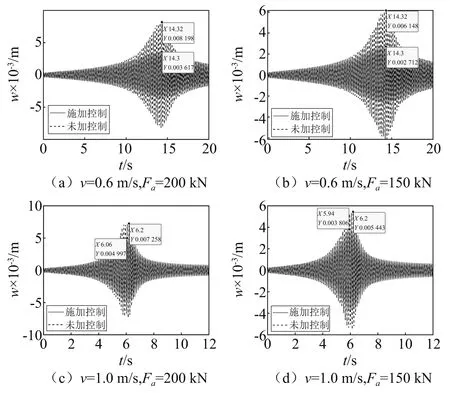
图7 不同工况下振动响应

从式(32)可知，根据未来N个时刻的响应计算对应的最优控制力序列，因此预测步数N和时间步长Δt必定会影响最优控制力，有必要分析N和Δt对振动控制的影响。保持桥梁推送速度和激励力不变，分别改变预测步数和时间步长进行仿真对比。图8是时间步长保持在0.02 s，不同预测步数对振动峰值的影响结果图，图9则是预测步数固定为5步，不同时间步长下振动峰值变化曲线结果图。

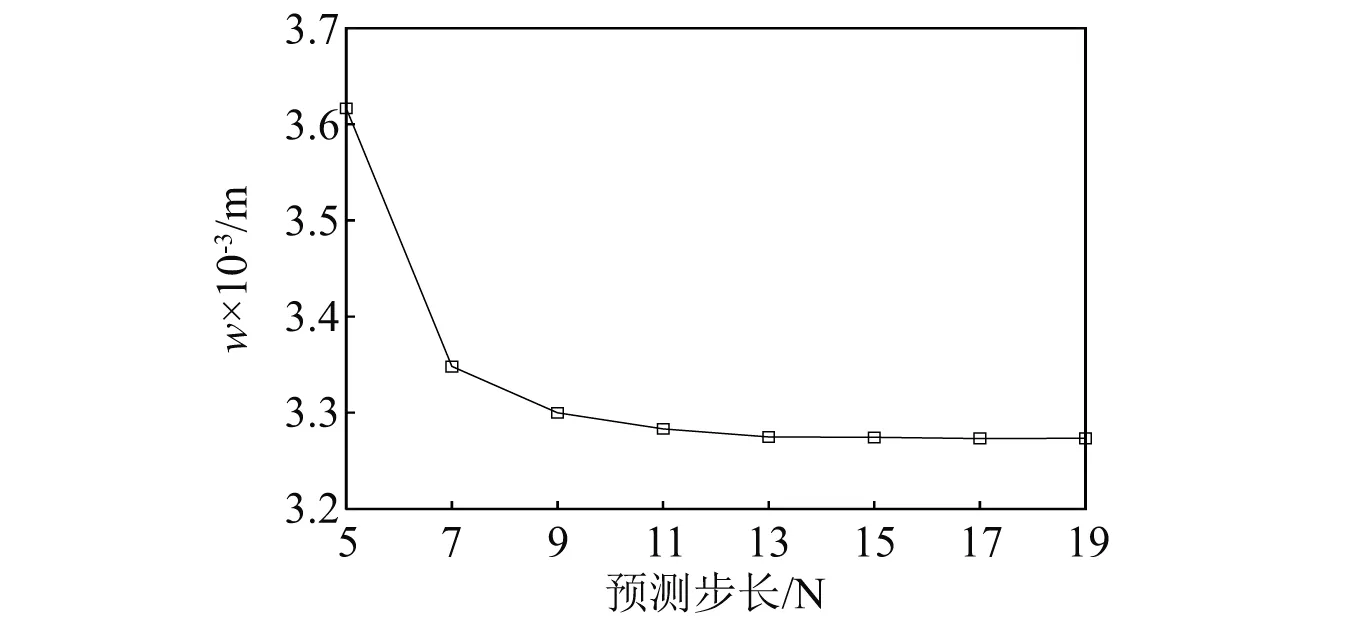
图8 不同预测步长下的振动峰值

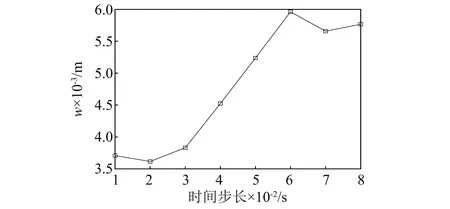
图9 不同时间步长下的振动峰值

首先从图8中可以清晰的看到当预测步数从10增加到19的时候，振动响应曲线几乎没有太大的区别，而预测步数从5增加到10的时候，振动控制效果显著提高。所以随着预测步数N的增加，图8的振动峰值的总体趋势是先减小然后保持稳定，最后几乎不随着N值的变化而变化，这也是因为预测步长过大导致预测模型失败，同时随着预测步长的增加，相应的计算负担也随之增加；另外图9的振动峰值变化曲线表明随着时间步长的增加，振动峰值也随之增加，即振动抑制效果下降，这也是因为时间步长的增加等同于增加预测步数，自然也会出现预测过多产生的预测失效结果。此外当时间步长过大时还会出现计算精度较低、时延明显等现象。因此根据上述分析对比，综合考虑计算负担以及控制效果，预测步数不宜超过10，时间步长不宜超过0.03 s。

5 结 论

本文首先将某型架桥车的推送过程简化为轴向移动悬臂梁系统，然后基于拉格朗日方程推导了模型的时变动力方程，并采用计算相对简单的幂级数函数来拟合悬臂梁的振型函数，避免了大量的三角函数计算，从而提高时变动力方程的求解速度。

接着通过分析架设参数对桥梁振动的影响和主动控制研究，得到以下结论：

(1)在推桥过程中，只有一阶模态会被激发，从而形成以一阶模态为主导振型的共振特点。因此为了尽量减少桥梁推送过程中的振动情况，应尽量避开桥梁一阶模态的共振频率，根据桥梁一阶模态频率随桥梁长度的变化规律可以发现，在桥梁推桥初始阶段，由于桥梁长度较短，一阶模态频率远高于桥梁推送时产生的激励力频率，此时应以最高架桥速度进行推送，当桥梁外伸长度超过8 m后，需要慢慢降低架桥速度来避开此时桥梁的一阶模态频率。通过理论分析，为实际架桥的速度控制提供了理论指导。

(2)基于Newmark法的模型预测控制能够有效的降低推送过程中桥梁的振动峰值，通过先预测结构未来的动态响应，再确定当前时刻的最优控制力，控制效果明显优于基于全局的最优控制，振动抑制效果最高可达55.9%；在改变推桥速度和桥梁所受激励力的幅值后，该控制策略仍能够有效的对共振区振动进行抑制，表明基于模型预测的主动控制鲁棒性较好；最后分析了控制参数中最重要的预测步数对控制效果的影响，通过数值分析对比给出预测步数的推荐值，为实际设计控制器提供参考。