基于离散平整度指数的城市道路舒适性预估方法

关丽敏，汪贵平，朱进玉，吴荻非

(1.长安大学 电子与控制工程学院，西安 710064；2.同济大学 道路与交通工程教育部重点实验室，上海 201804)

行驶舒适性是反映驾驶员和乘客行驶质量的重要参数，亦是道路服务能力的直观反映。路面平整度是行驶舒适性的重要影响因素[1]，颠簸的路面会显著增加车身的振动幅度，影响行驶质量，甚至危害驾驶安全。对城市道路的行驶舒适性进行科学的评价预估，进而采取有效措施避免严重行驶颠簸，可有效提升行驶质量，降低事故风险。

近年研究表明，道路平整度与车辆行驶舒适性具有明显的相关性，利用现场测试或仿真试验方法构建平整度指标与舒适性指标之间的数学关系，可用于有效预估不同场景下的行驶舒适性，其中应用最广泛的指标是国际平整度指数[2](international roughness index,IRI)以及ISO 2631-1中使用的加权加速度均方根指标(aw)[3]。Peter[4]对近20年的相关研究进行总结，指出IRI与aw呈良好线性关系，但相关参数受车型、车速影响显著。尽管IRI指标在行驶舒适性预估方面表现良好，但现有研究多针对匀速、长距离的行驶场景，对于交叉口频繁、车速变化剧烈的城市道路场景考虑欠缺。IRI表征的是一段距离内车辆悬架颠簸的累计值，难以反映短距离路段的局部不平整特性，且我国现有的公路技术评定标准多采用100～1 000 m的IRI指标作为平整度评价依据，无法有效反映路段局部颠簸对行驶舒适性的影响。Abudinen等[5]基于IRI指标研究了城市道路的舒适性评估方法，结果表明IRI与加权加速度均方根值的线性关系显著性明显偏低。

针对城市道路这种路段长度不等、速度分布离散的场景，目前还尚无通用的平整度表征方法，而针对行驶舒适性的研究也较为缺乏。但对于短距离路段局部不平整性的表征，部分学者提出了针对性的平整度评价指标，包括波音公司提出的波音平整度指标(boeing bump index，BBI)、Smith提出的轮廓指数(PrI)。在美国部分地区，基于IRI的局部平整度指数(7.62 m的IRI指数)也通常被辅助用于表征路面的局部情况。Zamora Alvarez等[6]于2015年提出的离散平整度指数(discrete roughness index，DRI)是近年来具有突破意义的平整度指标之一，其不仅可以有效表征路段的局部不平整特征，不受路段长度影响，且与IRI也有良好的换算关系，对于城市道路行驶舒适性的预估具有良好的适用性。相应的，现有行驶舒适性研究多采用的加权加速度均方根指标(aw)也多用于表征长距离、长时间的振动颠簸情况，其使用平均算符对较长领域内的振动信息进行整合，无法反应局部颠簸、短距离不平整引起的短时振动特征[7]，难直接应用于城市道路行驶车辆的舒适性表征。对此，本文采用了ISO 2631-1中定义的最大瞬时振动指标(maximum transient vibration value，MTVV)对该场景下的行驶舒适性进行描述，相较于加权加速度均方根，该指标可反应短时、剧烈振动引起的舒适性，对于城市道路适用性更强。

综合城市道路路段的特点以及现有基于IRI行驶舒适性评价方法的不足，本文基于实测的城市道路高程数据，采用MATLAB/Simulink构建8自由度整车振动仿真模型，解析代表车型在城市道路上行驶的座椅竖向加速响应。选用DRI指标和ISO 2631-1中使用的最大瞬时振动指标分别表征短距离路段的局部不平整性和瞬时行驶舒适性，进而详细分析车速、轮迹、时长的影响，构建城市道路舒适性预估模型和方法，并利用示例路段数据提出该模型对于行驶舒适性保障的应用形式。

1 路面平整度指数与舒适性评价标准

1.1 国际平整度指数

国际平整度指数的计算基于标准1/4车模型，其表征的是单位距离内、80 km/h行驶速度下车辆悬架颠簸的累计值。其计算模型如图1所示，图中,Ms,Mu，Ks,Cs,Kt分别指代簧上质量、簧下质量、悬架弹簧系数、悬架阻尼系数、轮胎弹簧系数[8-9]。

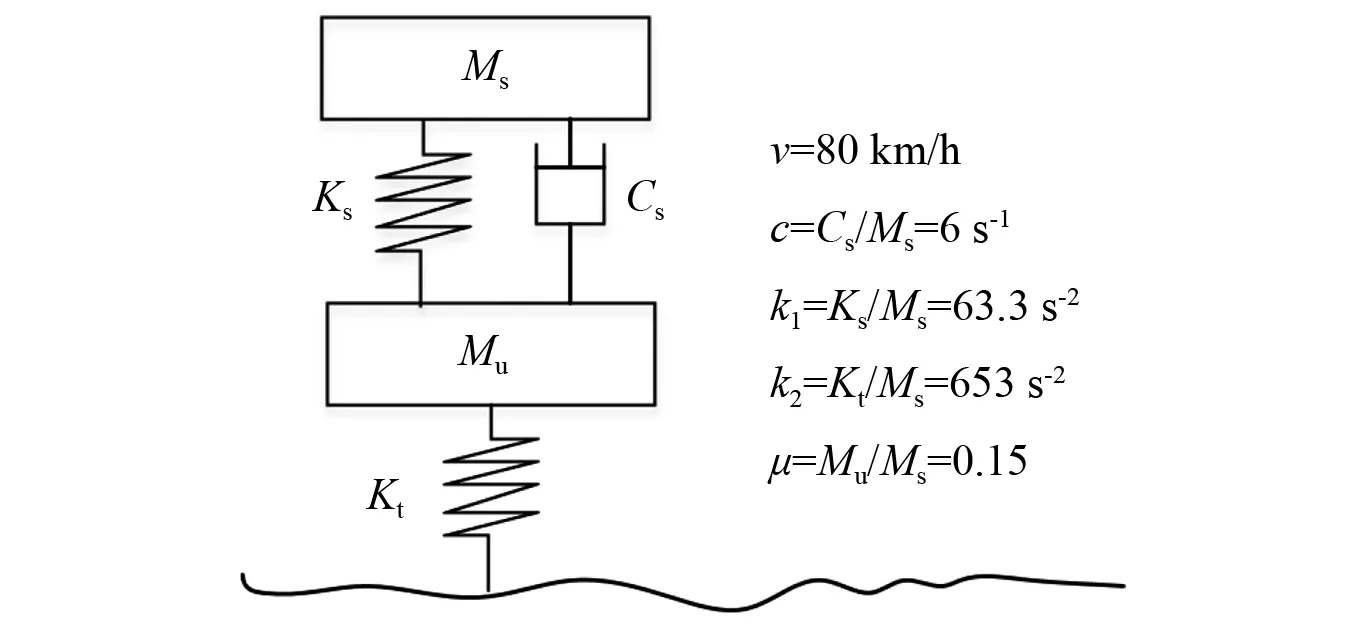
图1 1/4车模型

IRI的计算公式为

(1)

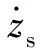
(3)

式(3)所示即为车辆簧上质量与簧下质量的竖向速度差，对该状态空间方程进行数值求解即可计算得到IRI指标。对于城市道路，其IRI指标通常在0～12 m/km。IRI越小，路面越平整，反之路面越颠簸。

1.2 离散平整度指数

离散平整度指数的计算同样基于1/4车模型。DRI的计算原理如图2所示。DRI可以看作IRI在距离上的离散结果，其表征的是具体点位的平整程度而非一段距离的平均结果。

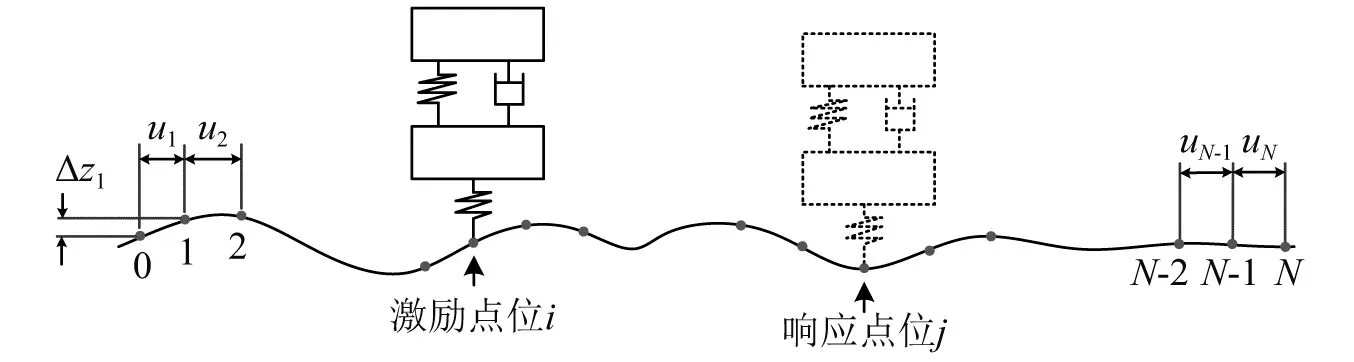
图2 DRI计算原理

如图2所示，首先将路段分割为多个路段区间，对应图中路段点位0～N。在1/4车模型计算中，点位j位置处悬架系统的响应可看作前序点位0～j-1路面高程的激励结果。随后定义激励点i～响应点j的响应系数fij，如式(4)所示

(4)

式中：Δzi为点位i～i-1的高程差;Δti为时间颗粒度；函数h(tj-ti)为ti时刻激励对应tj时刻的激励响应函数。假设整个测试路段有N个计算位点，则fij应满足

(5)

式(5)和式(6)中的响应系数fij可看作i位点激励对于j位点响应的贡献程度。因此，针对某激励位点i，可以计算其对所有响应点的平均贡献程度，定义其为离散平整度指数DRI。DRI数值越大，即表明该激励位点对整路段的平均贡献程度越大，进而说明该位点对应的局部不平整更显著。由此定义DRI计算公式为

(6)

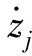
(7)

因此，DRI不仅可进一步表征路面的局部平整状况，且在长距离路段上与IRI有良好的换算关系，适用于短距离、速度差异明显的城市道路。

1.3 行驶舒适性指标

现有的车辆行驶舒适性评估多基于ISO 2631-1的标准，采用加权加速度均方根值aw表征人体的行驶舒适性。由于路面不平整的影响多表现在垂直方向，对于横向和侧向振动影响相对较小，故本文仅分析路面平整度引起的竖向振动，其计算公式为

(8)

式中：T为振动时长;awz为Z轴(竖向)方向上的加权加速度均方根。awz通常用以表征长距离、较长时间上的振动状态，对于短距离路段、瞬时振动状态，ISO 2631-1基于加权加速度均方根提出了“最大瞬时振动指标”用于表征瞬时的振动程度，其计算公式为

(9)

MTVV=max[awz(t0)]

(10)

式中：t0为计算时刻;τ为积分计算的瞬时时长，通常选用为1 s。此外，ISO 2631-1规定了MTVV和aw的经验换算关系，如式(11)所示

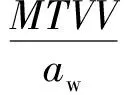
(11)

基于上述舒适性指标，ISO 2631-1亦提出了对应的舒适性等级和判断标准[10]，如表1所示。

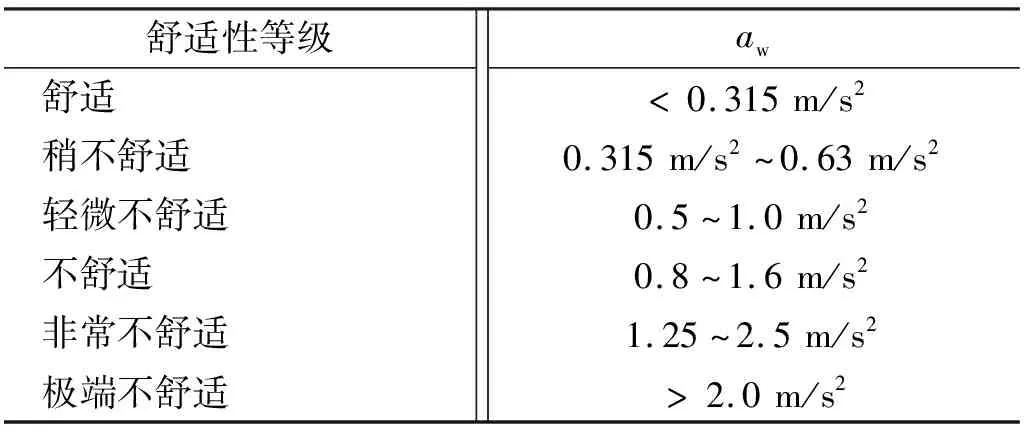
表1 舒适性等级及判别标准

2 数值仿真

2.1 车辆振动模型

在车-路耦合振动分析中，车辆振动模型通常模拟为多自由度弹簧-阻尼模型。早期为简化计算，通常将车辆振动模型简化为2自由度的1/4车模型，仅包含一个簧上质量和簧下质量用以表征单个悬架结构。尽管1/4车模型可分析基本的车辆振动响应，但无法表征车辆前后轴、左右轮之间的相互影响。针对上述考虑，半车模型、整车模型也在大量研究中得以应用。在行驶舒适性评估中，车辆左右轮迹的平整度、前后轴对车身的相互作用均会影响车辆振动形态，故本研究采用了如图3所示的8自由度整车模型进行仿真分析。该车辆振动模型考虑了左右轮迹对车身振动的影响，可有效模拟分析车辆的侧倾和俯仰姿态。同时，该模型单独定义了一个自由度用以模拟车辆座椅并求解相应的竖向加速度。通过调整座椅的横向和纵向位置，可分别求解驾驶位和乘客位置的竖向加速度。

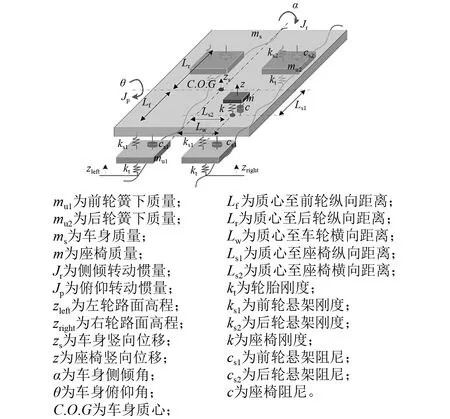
图3 8自由度整车模型

对于图3所示的车辆振动模型，其运动方程可表示为[11]

(12)

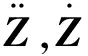
(13)

式中:kt为轮胎刚度，并假设四个轮胎刚度相同；v为车辆行驶速度；l为轴距。通过构建式12的状态空间方程，即可在MATLAB/Simulink中构建车辆模型对座椅加速度响应进行求解。本文选用某典型双轴车辆作为研究车型，其模型参数引用自Cantisani等[12]于2010年的实测标定结果。仿真计算过程中，时间分析步长设置为0.001 s，且假设车辆保持匀速状态平稳行驶，不考虑加减速、转向等行驶状态。

2.2 路面高程

本研究选用了国内某市内108个城市道路路段的实测高程数据作为系统激励以求解车辆的振动响应。路段长度从58～1 282 m不等，平整度指数在0.82～12.95 m/km。路段的高程数据采用激光检测车进行测量，测量结果覆盖了左右轮迹位置。受车速、路表异物、裂缝的影响，激光检测车测量的高程数据采样点间距并不一致(0.1～0.3 m)，且局部存在异常值。为适应车辆振动的Simulink求解，首先采用三次样条插值对实测高程数据进行预处理，将采样点间隔统一为0.01 m，对应空间采样频率为100 m-1。随后进行滤波处理，以消除局部异常高程值。IRI指标的计算通常采用Sayers等提出的25 cm均值滤波对路面高程进行平滑处理，但均值滤波方法仅能剔除部分高频噪声，无法有效消除局部异常高程值。为兼顾平滑处理和异常值剔除，本研究选用小波滤波器对原始高程数据进行滤波处理。小波分解尺度由路面高程的空间频率决定，为确定空间频率选取范围，基于图3所示的整车振动模型，计算座椅-路面高程频响函数，如式(14)所示

(14)

式中：aseat(ω)和zroad(ωs)分别为座椅加速度频谱和路面高程的空间频谱；ωs为空间频率，m-1。采用单位脉冲函数对式(12)进行求解，可得到不同速度下的频响函数，如图4所示。

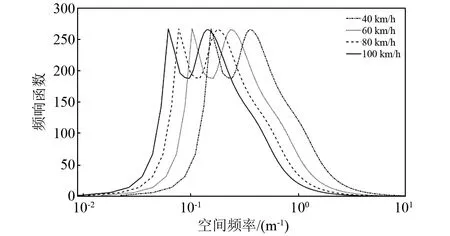
图4 车辆座椅频响函数

由图4所示，在40～80 km/h的速度区间内，频响函数的幅值主要集中在[0, 6 m-1]频段内，表明路面高程的高频部分(>10 m-1)对车辆振动无显著影响。因此，选用5层小波分解对路面高程数据进行滤波处理，并选用第5层分解结果作为滤波结果，对应的频率范围为[0,6.25 m-1]。小波滤波器和移动均值滤波的平滑结果，如图5所示。结果表明小波滤波器可有效的剔除17 m位置处的异常高程变化，且能取得较好的平滑效果。

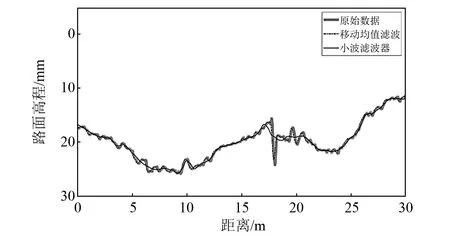
图5 路面高程滤波结果

3 模拟计算与结果分析

3.1 仿真求解结果

选取某城市470 m长的路段作为案例，其左右轮迹的IRI分别为3.34 m/km和3.49 m/km，采用1.0 m的路段分割长度计算对应的DRI指标，并利用仿真分析模型计算对应的座椅竖向加速度和瞬时加速度均方根值，行驶车速设置为80 km/h，且暂不考虑车速变化的影响。计算结果如图6所示。

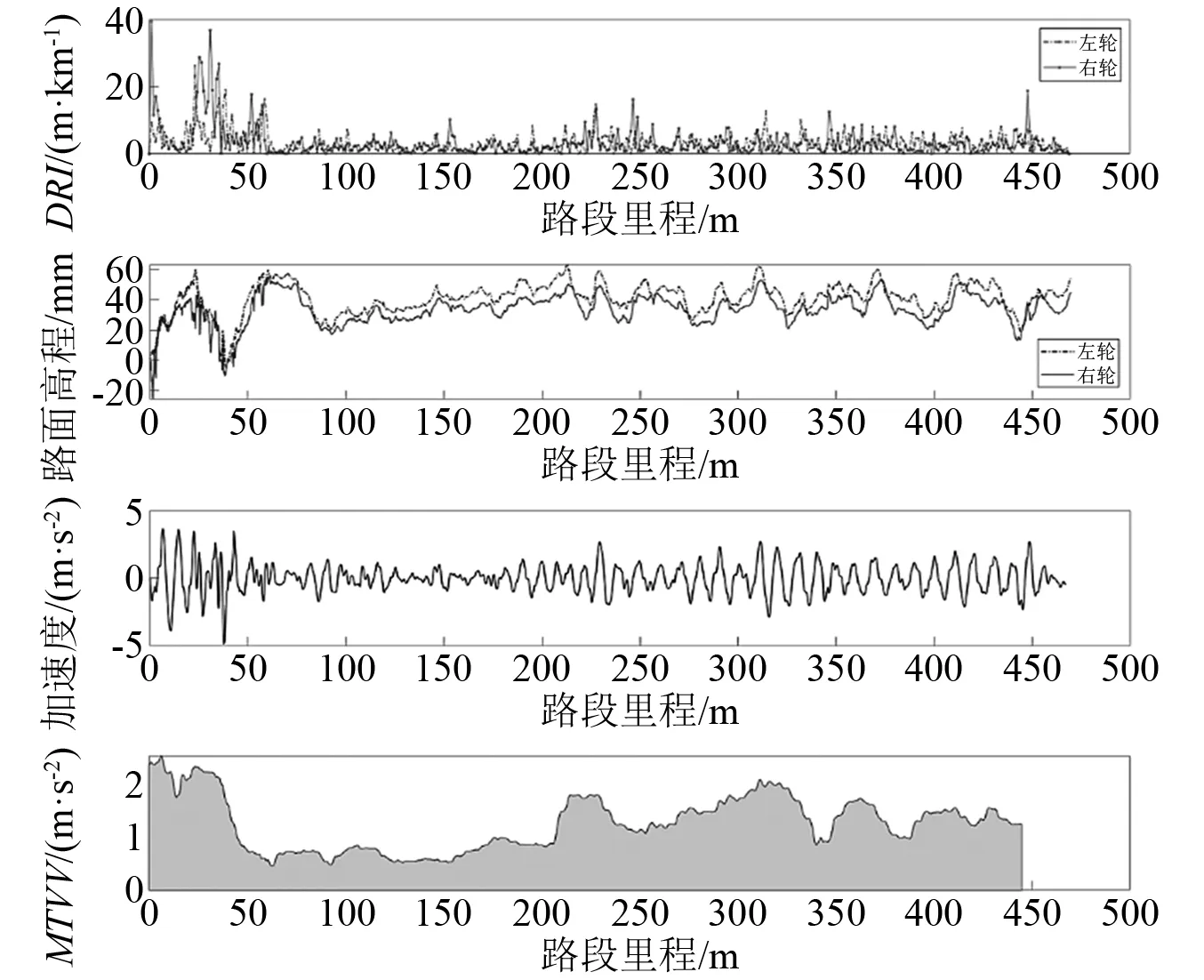
图6 仿真计算结果

如图6所示，尽管路段的IRI相对偏小，但其局部区域的DRI明显偏大，主要分布于0～50 m路段内，由此产生的座椅竖向加速度和瞬时加速度均方根值也明显增大。基于式(9)可计算得到整路段的加权加速度均方根值为0.937 m/s2，对应的舒适性等级为“轻微不舒适”。当在0～50 m和300 m位置处，瞬时的加权加速度均方根均超过了2.0 m/s2，经式(11)换算后仍达到了“非常不舒适”的量级。由图6可见，DRI在路段上分布趋势与瞬时加权加速度均方根的分布规律具有一定的一致性，因此可通过构建DRI与瞬时加权加速度的关系，实现短距离路段、局部不平整的行驶舒适性预估和评价。

3.2 DRI与瞬时舒适性的关联分析

采用式(11)提出的MTVV指标表征瞬时状态的行驶舒适性。依据108个城市道路路段的高程数据，计算各路段的DRI指标和MTVV指标，并对车速、瞬时时长等因素进行定量分析，进而构建DRI和MTVV在不同工况下的数学关联。综合考虑城市道路速度分布的范围、离散型以及人体对瞬时冲击的感受，分别计算40 km/h,60 km/h,80 km/h,100 km/h的车速工况，其余车速对应的计算结果依据上述工况进行插值求解；瞬时振动时长考虑1 s,2 s,4 s三个工况，依据不同的时长和车速，计算对应距离内的离散平整度指数平均值(DRIavg)和IRI表征路段的平整情况。

除车速、瞬时时长的影响外，左右轮的高程差异亦会对车辆振动有显著影响。杜豫川等[13]在平整度检测研究中指出，受车身刚体的影响，在车辆一侧由于路面高程变化而产生加速度值时，会在另一侧产生一个响应加速度值，即任何一侧的加速度实测值都是叠加产生的结果，且路段越短，左右轮的相互影响越显著。不同路段长度计算的左右轮平均DRI的散点分布，如图7所示。

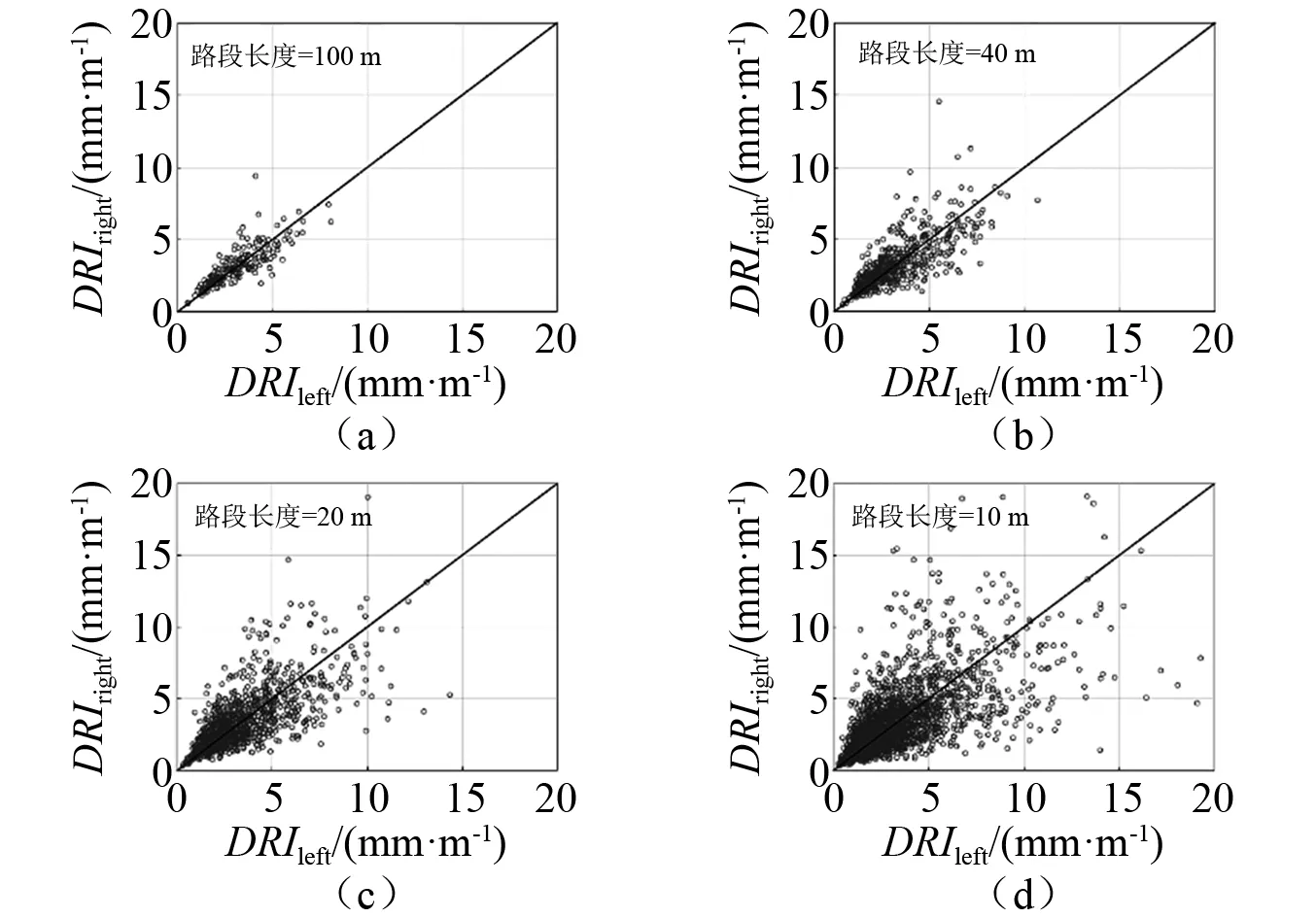
图7 左右轮平整度对比

结果表明，路段长度越大，计算得到的平整度指标越接近，而路段长度越小，其平整度指标差异明显。因此，针对短距离路段的行驶舒适性分析，有必要综合考虑左右轮迹的相互影响。

既有大量研究表明，IRI与加权加速度均方根值存在良好的线性关系，其拟合优度指标(R2)在0.75～0.99不等。但对于局部颠簸，DRI指标与加权加速度均方根值的关联并不显著。因此，本研究选用幂函数对DRI与MTVV的关联性进行拟合，如式(15)所示

(15)

式中,a1,a2,a3为拟合参数。进一步的，计算得到各速度工况、瞬时时长工况下DRI与MTVV的拟合结果，如表2所示。IRI与MTVV的关联性同步计算用以对比。

由表2可见，DRI与MTVV的关联性较IRI而言更明显，拟合优度甚至可超出0.1以上，尤其对于高车速工况。速度、瞬时时长、左右轮迹的影响均可通过拟合的参数予以表现：速度越高，拟合参数a1越大，表明平整度对于瞬时舒适性影响越显著，且在60 km/h车速的工况下，其拟合效果越好；瞬时时长越大，拟合效果越好；拟合参数a2,a3表明了左右轮迹平整度对瞬时行驶舒适性的影响程度，速度越大，驾驶位的MTVV受对应轮迹(左轮轮迹)的影响更小，表明在低速工况下，车内的行驶舒适性主要受一侧轮迹平整度影响，而在高速工况下，车内行驶舒适性更表现为两侧轮迹的耦合影响结果。综合表2的计算结果，为进一步分析短距离路段上路面平整度与舒适性的关联，选用2 s瞬时时长工况下的拟合结果作为行驶舒适性的预估模型，进而构建行驶舒适性的预估标准。

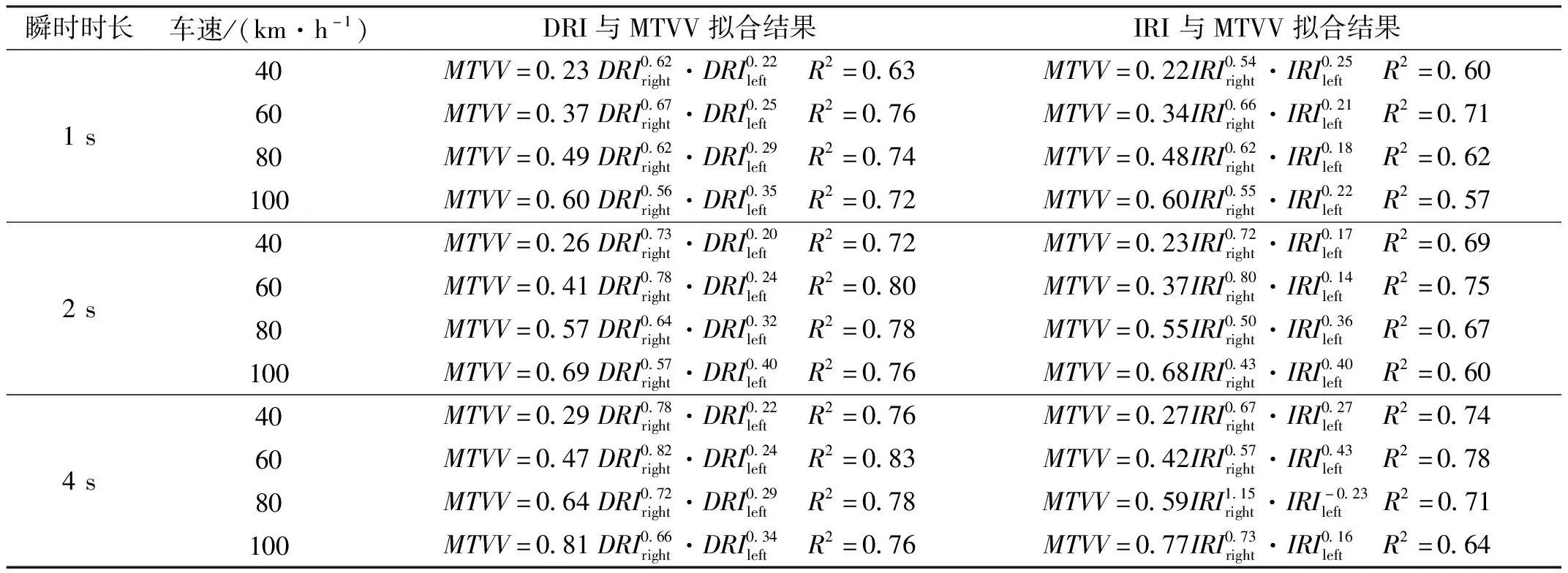
表2 瞬时舒适性预估模型

3.3 速度影响下的瞬时舒适性预估标准

综合表2中计算得到的MTVV预估模型和表1中定义的舒适性评价标准，同时依据式(11)定义的瞬时舒适性与加权加速度均方根的换算关系，可进而构建不同速度工况下的行驶舒适性预估标准。前述研究主要针对驾驶位(左侧)的舒适性开展计算分析，考虑到乘客位(副驾驶位)与驾驶位呈对称关系，因此基于表2中的拟合结果，调换拟合参数a2，a3的位置，即可得到乘客位的瞬时舒适性预估模型。

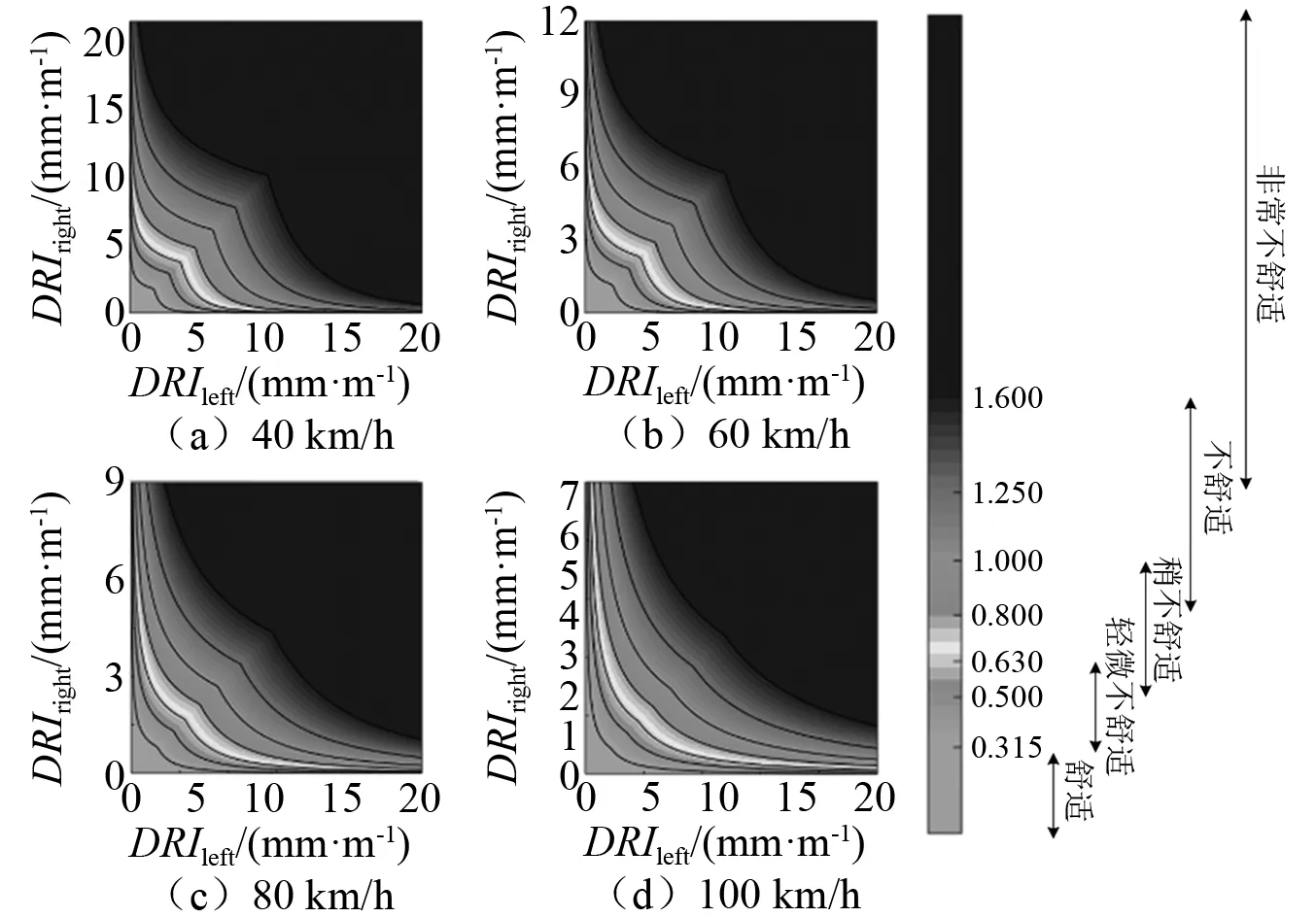
图8 不同舒适性等级对应的DRI阈值

3.4 基于DRI的城市道路舒适性预估与速度规划

基于表2得到的舒适性预估模型和图9定义的舒适性预估标准，可实现对已知平整度路段的行驶舒适性预估，进而可研究城市道路路段的舒适驾驶策略，即通过优化速度控制以保证良好的行驶舒适性。采用2 s-MTVV作为瞬时舒适性评价指标，选取某1.2 km长示例城市道路路段(左右轮迹IRI分别为5.8 m/km和4.9 m/km)，计算不同舒适性等级下的速度阈值，如图9所示。

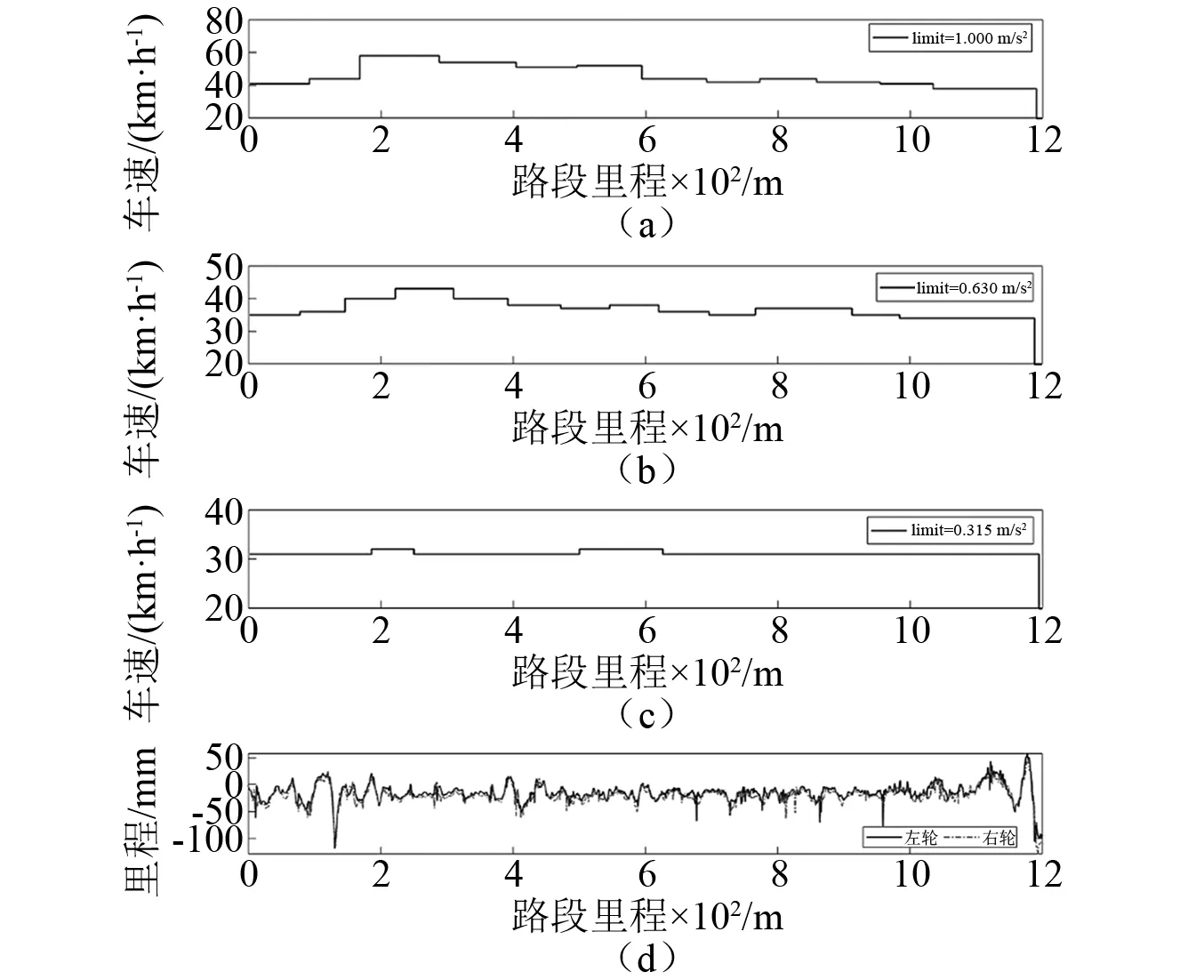
图9 不同舒适性等级下的速度阈值

图9(a)～图9(c)分别为保持舒适性等级为“舒适”、“稍不舒适”和“轻微不舒适”时的速度阈值曲线，当行驶速度低于该速度曲线时，即可保证对应的行驶舒适性。该速度阈值曲线可行驶舒适性的保障提供指导和建议，但在实际车辆行驶过程中，车辆为保障竖向振动舒适性同时，还应考虑加减速导致的纵向振动舒适性。假设车辆采用线性加减速模型，即加速度为ac，则可依据ISO 2631-1计算得到加权后的MTVV，如式(16)所示

(16)

式中，wd,k和wk,k分别为纵向和竖向振动的权重，其中wd,k=1.4，wk,k=1.0。加权得到的MTVVcob亦需满足舒适性等级要求，即

(17)

式中,alimit为表1中对应的各舒适性等级的加权加速度阈值。为保证车辆行驶处于对应的舒适性等级，进一步求解式(17)，可得

(18)

因此，在实际行驶过程中，车辆需要综合局部的平整度状况，同时考虑速度阈值曲线和式(18)中对于加减速的要求，优化车辆的速度控制策略以保障良好的行驶舒适性。

4 结 论

本文针对城市道路的平整度分布特点，基于ISO 2631-1选用最大瞬时振动指标作为舒适性评价标准，引入离散平整度指数构建城市道路行驶舒适性的预估流程和方法，利用MATLAB Simulink搭建8自由度整车仿真模型，依托于国内某市实测的108个城市道路高程数据对驾驶位和乘客位的竖向加速度进行仿真求解，在此基础上采用幂指数构建基于DRI的舒适性预估模型。结果表明，DRI相对于IRI对于短时、短距离的行驶舒适性预估效果更好，表现为DRI与MTVV的拟合优度较IRI高出0.1以上。速度、瞬时时长对于预估模型影响显著，速度越大，行驶舒适性受局部平整性影响更显著。在短距离路段上，左右轮迹的平整度差异较长路段更明显，进而显著影响舒适性预估模型，且速度越大，左右轮迹对于座椅加速度的耦合影响越明显。最后，基于ISO 2631-1中定义的舒适性等级和评定方法，选用2 s-MTVV对应的舒适性预估模型构建不同行驶速度下的DRI等级标准，并基于示例路段提出了行驶车辆的速度规划策略。研究可为城市道路的舒适性评估和驾驶辅助策略提供一定参考。