基于滚珠丝杠副滚道磨损的摩擦力矩计算与试验

潘承莹，祖 莉，周长光，欧 屹

(南京理工大学 机械工程学院，南京 210094)

随着滚珠丝杠副的运转，滚珠不断运动致使滚道发生磨损，摩擦力矩会随之下降[1]。摩擦力矩作为滚珠丝杠副的重要性能，直接反映滚珠丝杠副的磨损和刚度[2]，具有重要的研究意义。

目前，滚珠丝杠副摩擦力矩的计算越来越受到关注[3]。日本某产品技术手册给出了考虑螺旋角和预紧力的摩擦力矩计算公式，但其忽略了接触角和滚道磨损的影响[4]；张佐营[5]分析了接触角与摩擦力矩的映射规律；吴长宏[6]研究了螺旋角与摩擦力矩的映射规律；然而都只是单因素的理论分析。赵哲等[7]考虑螺母滚道的磨损分析了预紧力与摩擦力矩之间的联系，但其忽略了丝杠滚道的磨损；张志强[8]定性分析了预紧力对摩擦力矩的影响，但没有建立摩擦力矩计算公式。上述研究中对摩擦力矩的分析大都只是单独考虑螺旋角、接触角和预紧力的影响，缺少能够综合考虑多因素的摩擦力矩计算公式。

滚珠丝杠副发生剧烈磨损时，摩擦力矩以及其他服役性能均无法满足使用需求，甚至出现故障情况，因此，为避免因剧烈磨损而影响使用，滚珠丝杠副服役时通常在稳定磨损阶段下运行。为了反映滚珠丝杠副服役过程中(稳定磨损阶段)滚道磨损情况以及摩擦力矩退化情况，本文综合考虑接触角、螺旋角以及滚道磨损量对摩擦力矩的影响，基于滚珠与滚道之间的变形量，通过计算磨损量，建立新的摩擦力矩计算公式，并开展4010型和4016型滚珠丝杠副摩擦力矩试验以验证本文模型的准确性。

1 滚珠丝杠副摩擦力矩理论计算

1.1 滚珠与滚道的弹性接触变形

滚珠丝杠副不受载时，滚珠与滚道之间是点接触，在法向载荷作用下，滚珠与滚道之间的接触变为面接触[9]，如图1所示。

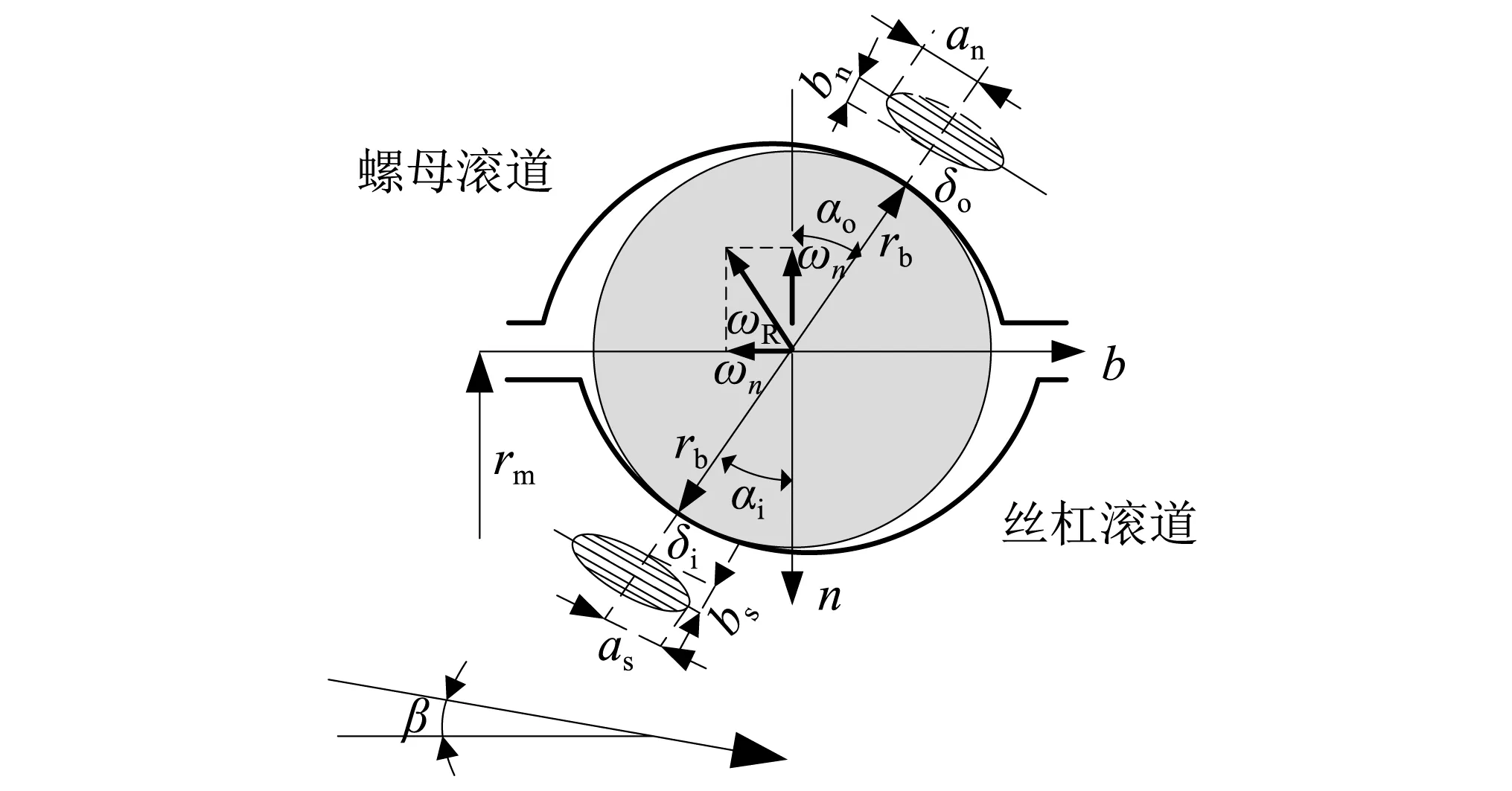
图1 滚珠与滚道的接触示意图

弹性变形量δ可根据赫兹接触理论[10]求得

(1)

式中：K(k)和E(k)为第一类、第二类完全椭圆积分；k为接触椭圆参数，由式(2)求得[11]；E′为当量弹性模量；∑ρ为滚珠与滚道接触区域的主曲率和；Q为法向载荷。

(2)

E′可通过丝杠螺母的的泊松比和弹性模量求得

(3)

式中：μi，μo分别为丝杠和螺母滚道泊松比；Ei和Eo分别是丝杠和螺母滚道弹性模量。

联立式(1)～式(3)，滚珠与滚道的接触变形量分别为

(4)

式中：δi和δo分别为滚珠与丝杠和螺母滚道的接触变形；∑ρi和∑ρo分别为滚珠与丝杠和螺母滚道接触区域的主曲率和；Qi和Qo分别为丝杠和螺母滚道接触区域法向载荷。

1.2 丝杠副磨损量的计算

假设滚珠受载均匀，滚珠与滚道接触面的磨损量可以写为

(5)

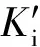
滚珠与滚道接触面面积表示为

(6)

式中：ai和ao分别为丝杠和螺母滚道接触椭圆面长半轴；bi和bo分别为螺母滚道接触椭圆面短半轴。

滚珠在螺母滚道上的滑动速度，可由式(7)求得[12]

(7)

式中：rb为滚珠半径；rm为丝杠半径；αi和αo为滚珠与丝杠和螺母滚道的接触角；β为螺旋角；ωm为滚珠公转角速度；ωs为丝杠角速度；ωt，ωn和ωb为滚珠自转角速度ωR在t，n，b三个方向的绝对速度分量，计算公式为[13]

(8)

(9)

式中：r′=2rb/rm；βu2为滚珠自转轴与t-b平面的夹角，其值近似45°；β2b为βu2在t-b平面的投影与b轴的夹角，实际研究中，β2b非常小，可以忽略不计。

滚珠与滚道的法向接触载荷可以写为[14]

(10)

式中：Fa为轴向载荷(当不受轴向载荷时，Fa为预紧力)；Z为滚珠个数。

滚珠在滚道中运动时，只有部分滚道与滚珠接触，滚珠与滚道实际接触情况的修正系数可由式(11)求得

(11)

式中，Li，Lo分别为丝杠、螺母有效行程。

将式(6)、式(7)、式(10)及式(11)代入式(5)，丝杠和螺母滚道的磨损量可以写为

(12)

故滚珠丝杠副磨损量Δδz为

(13)

式中，m为螺母的个数。

滚珠丝杠副磨损阶段的摩擦力矩是基于磨损量的计算得到，因此，在进行摩擦力矩分析之前需进行磨损量的计算。通过对多个滚珠丝杠生产厂家调研可知，目前行业内对轻预紧等级的4010型和4016型滚珠丝杠副的使用最为广泛，因此，本文选择以轻预紧等级滚珠丝杠副进行理论计算以及试验研究。由于滚珠丝杠副使用厂家的实际使用工况为润滑脂润滑，且生产厂家推荐的润滑条件也是脂润滑，为模拟使用情况下的滚珠丝杠副磨损情况，本文理论计算和试验所采用的4010型和4016型号双螺母滚珠丝杠副的润滑条件为脂润滑，根据文献[15]所列的磨损系数表，针对滚珠丝杠副的材料GCr15，磨损系数的取值范围为0.59×10-11～0.82×10-11，试验中需对滚珠丝杠副充分润滑，则滚珠丝杠副在运行中润滑条件良好，此时，磨损系数较小取值为0.6×10-11。4010型和4016型双螺母滚珠丝杠副具体参数如表1所示。

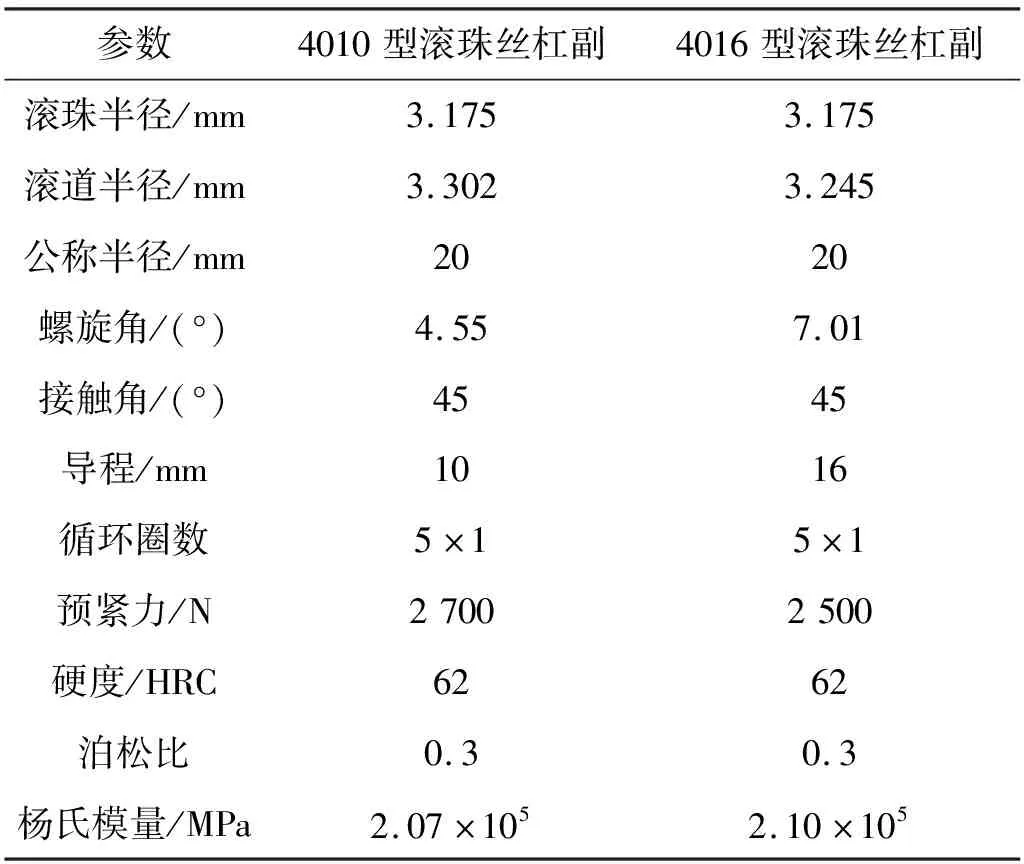
表1 4010型和4016型双螺母滚珠丝杠副参数

1.2.1 4010型丝杠副的磨损量计算

计算4010型滚珠丝杠副磨损量：①取时间t=17x(单位：h,每跑和17 h进行一次摩擦力矩试验，x为自然数，取1，2，3，…)，转速n=1 000 r/min代入式(12)，得到转速1 000 r/min下的4010型样件的磨损量；②取时间t=17x(参数与取值如前)，转速n=500 r/min代入式(12)，得到转速500 r/min下的4010型样件的磨损量；计算结果如表2所示。

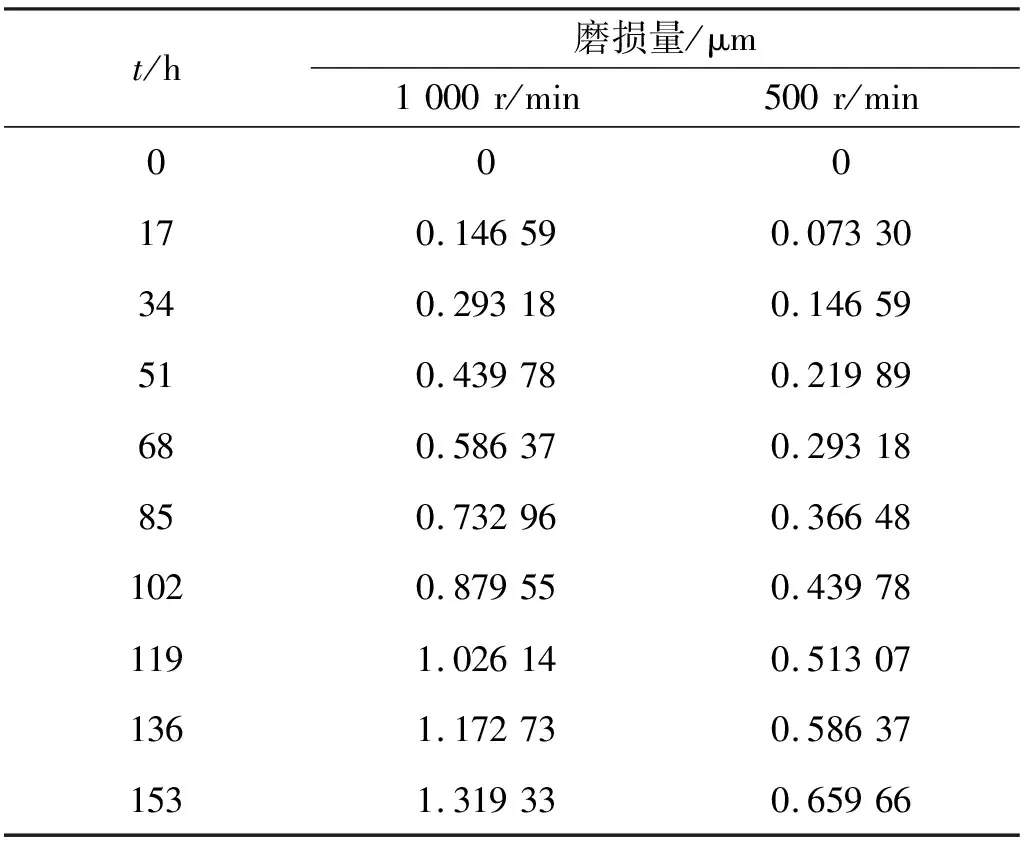
表2 4010型滚珠丝杠副磨损量计算值

1.2.2 4016型丝杠副的磨损量计算

采样点的选取对于摩擦力矩理论值与试验值拟合程度影响比较大，此处将4016型丝杠副采样取值与4010型作出区别，则4016型丝杠副采样点分段处理。

计算4016型双螺母滚珠丝杠副磨损量

(40 h以前每跑和5 h进行一次摩擦力矩试验，40 h以后每隔55 h进行一次摩擦力矩试验，x为自然数，取1,2,3,…)，转速n=1 000 r/min代入式(12)，得到转速1 000 r/min的4016型样件的磨损量；

(参数与取值如前)，转速n=500 r/min代入式(12)，得到转速500 r/min的4016型样件的磨损量。计算结果如表3所示。

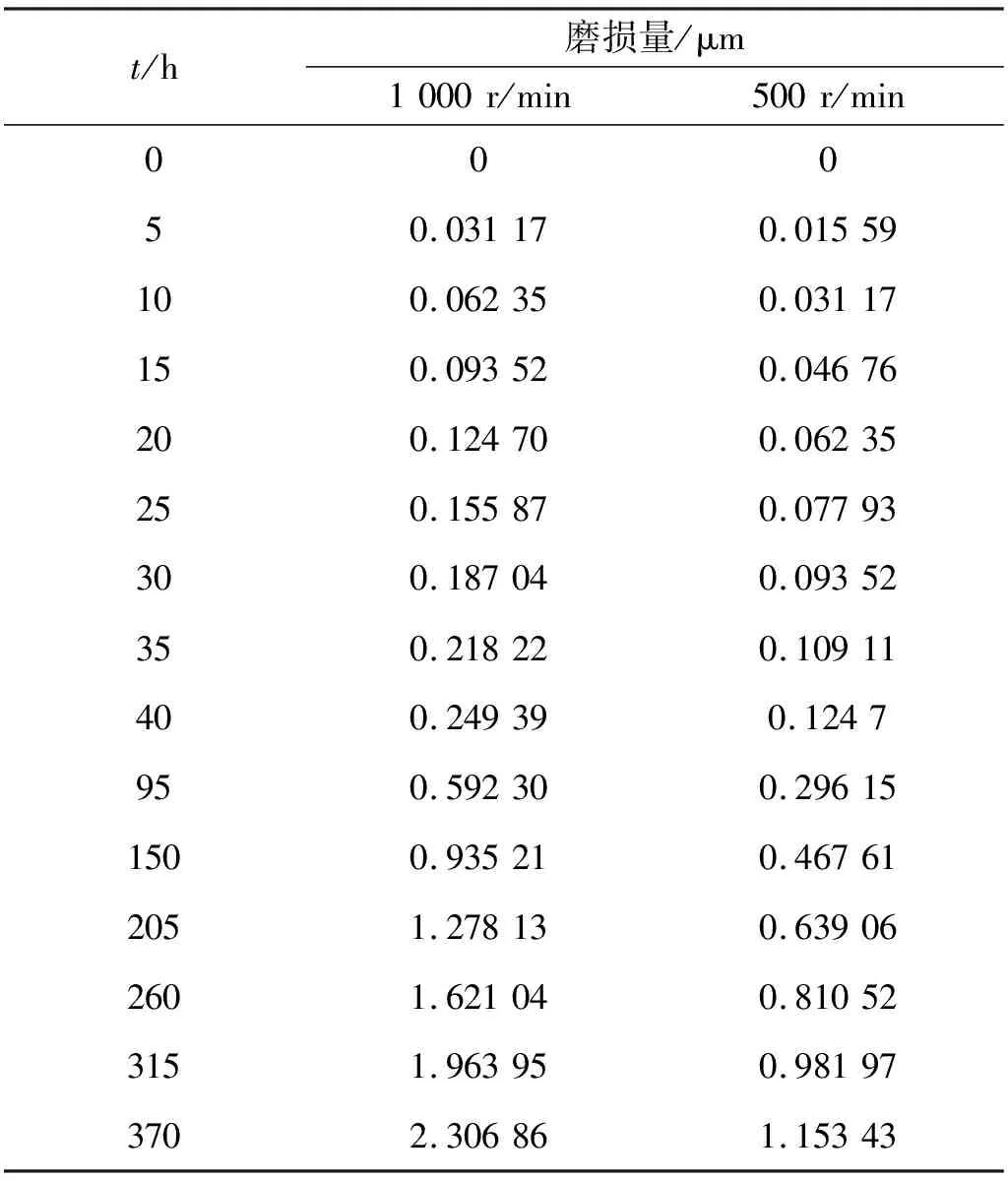
表3 4016型滚珠丝杠副磨损量计算值

1.2.3 理论磨损量分析

图2为4010型和4016型双螺母滚珠丝杠副磨损量的理论变化图，可以看出：①同一规格滚珠丝杠副在不同转速下的磨损情况不同，转速越高，磨损越快。运转相同时间，同一型号滚珠丝杠副在转速1 000 r/min下的磨损量是转速500 r/min时磨损量的两倍；②在同等转速下，不同型号滚珠丝杠副磨损情况不同，4010型磨损量变化的速度是4016型滚珠丝杠副磨损量变化速度的1.38倍。可见实际工况(转速)与结构参数(螺旋角、滚珠滚道尺寸、杨氏模量)会影响滚珠丝杠副的磨损量。

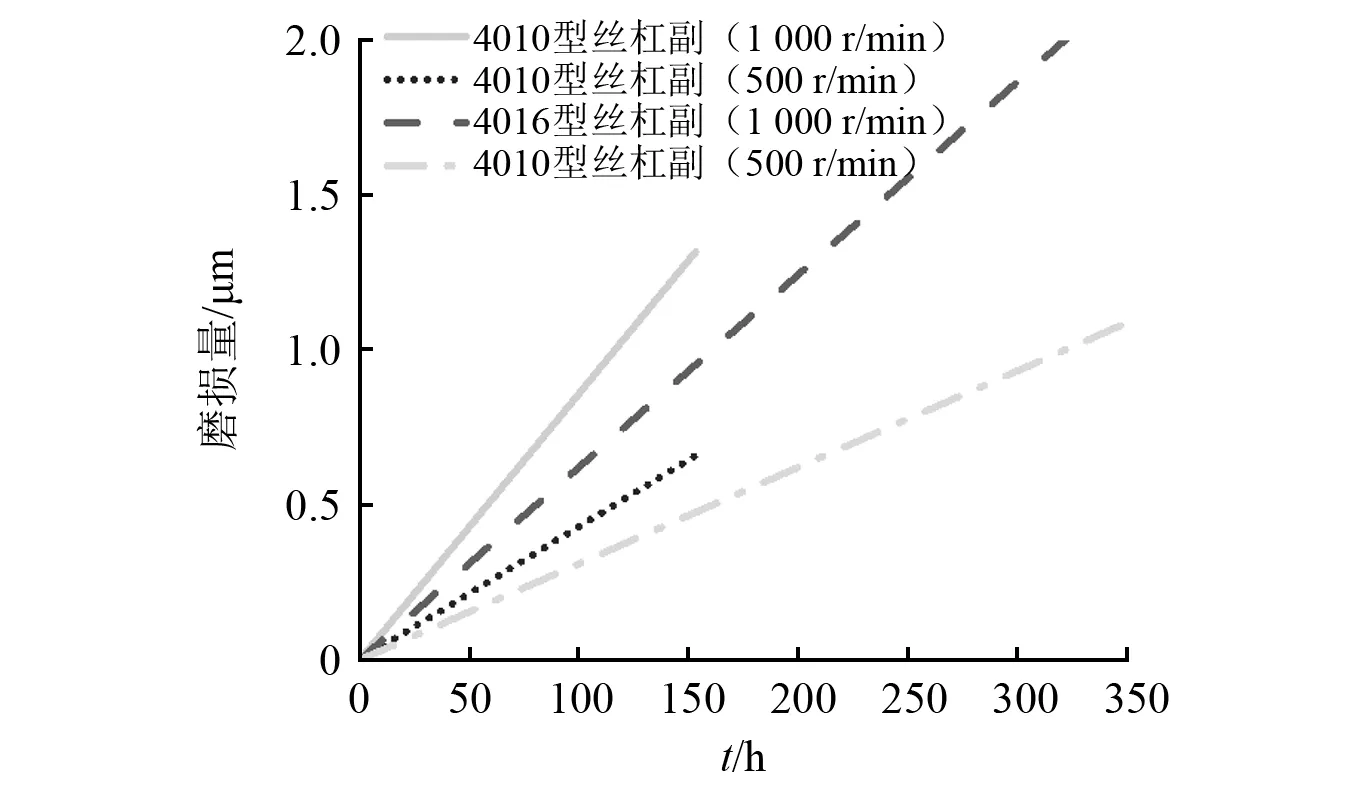
图2 滚珠丝杠副理论磨损量

1.3 基于滚道磨损的摩擦力矩的计算

滚珠丝杠副的摩擦力矩主要由丝杠滚道的摩擦力和螺母滚道的摩擦力产生的力矩构成，如式(14)所示。

(14)

式中：M为滚珠丝杠副摩擦力矩；Mo，Mi分别为螺母、丝杠滚道产生的摩擦力矩；FfA，FfB分别为滚珠与螺母、丝杠滚道的摩擦力；LA，LB分别表示螺母、丝杠滚道摩擦力的力臂。

图3为滚珠受力图，接触点与椭圆接触面中心点的距离相较于滚珠半径是极小的，此时将接触点等效成接触面中心。故滚道接触点A、B到丝杠中心的垂直距离(滚道摩擦力力臂)可以近似表示为

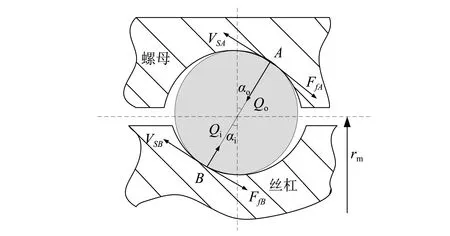
图3 滚珠的受力分析

(15)

而滚珠与滚道的摩擦力可表示为

(16)

式中，f为摩擦因数，根据赵哲等所列的摩擦因数表以及使用的脂润滑工况，摩擦因数取值为0.004。

将式(15)和式(16)代入式(14)可得滚道处的摩擦力矩为

(17)

随着运转时间的增加，滚道磨损越严重，会导致预紧力衰退，法向载荷改变。预紧力Fx的退化公式为[15]

(18)

式中：Fp为初始预紧力。

将式(18)代入式(10)可得出法向接触载荷的变化，并结合式(17)得出丝杠副滚道处的摩擦力矩

(19)

滚珠丝杠副摩擦力矩计算式(19)由丝杠滚道与螺母滚道两部分摩擦力矩构成，这两部分摩擦力矩都考虑了接触角、螺旋角和预紧力，其中预紧力与磨损量有直接的关联，故建立的摩擦力计算公式能够综合体现接触角、螺旋角与磨损量。

将表2及表3中磨损量计算值分别代入式(18)得到预紧力，再结合式(19)，得到4010型和4016型双螺母滚珠丝杠副摩擦力矩的理论值，计算结果如表4、表5所示。

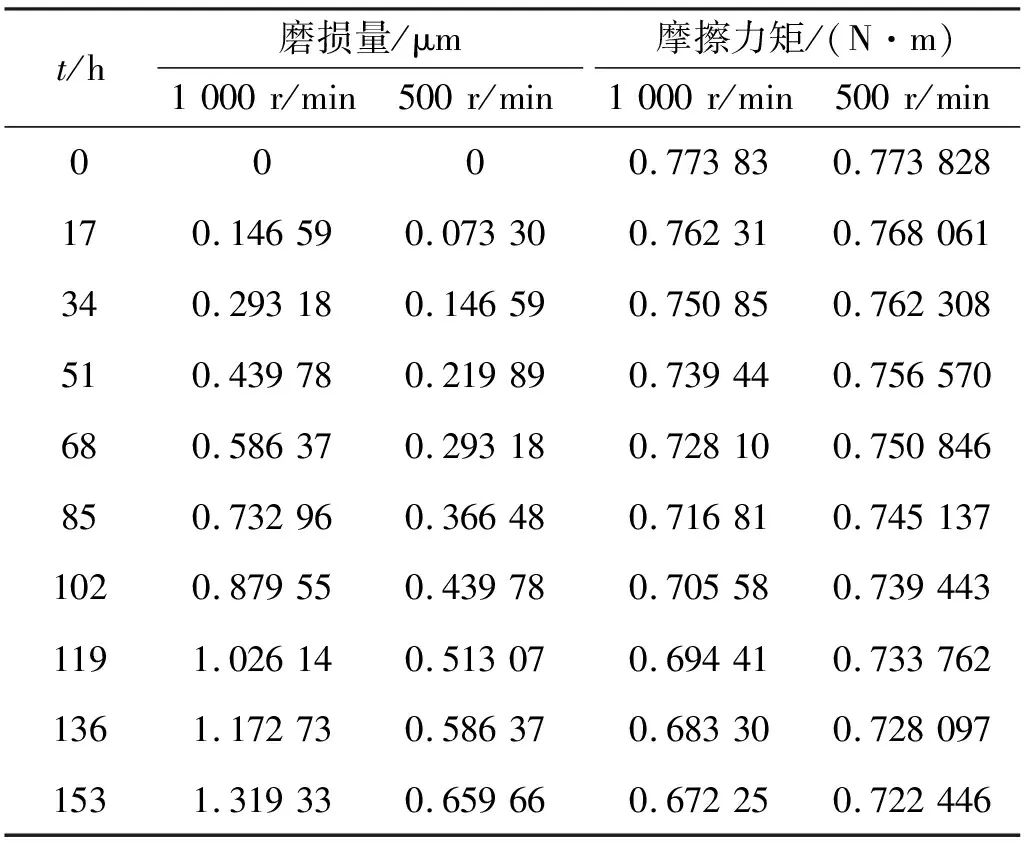
表4 4010型滚珠丝杠副摩擦力矩计算值

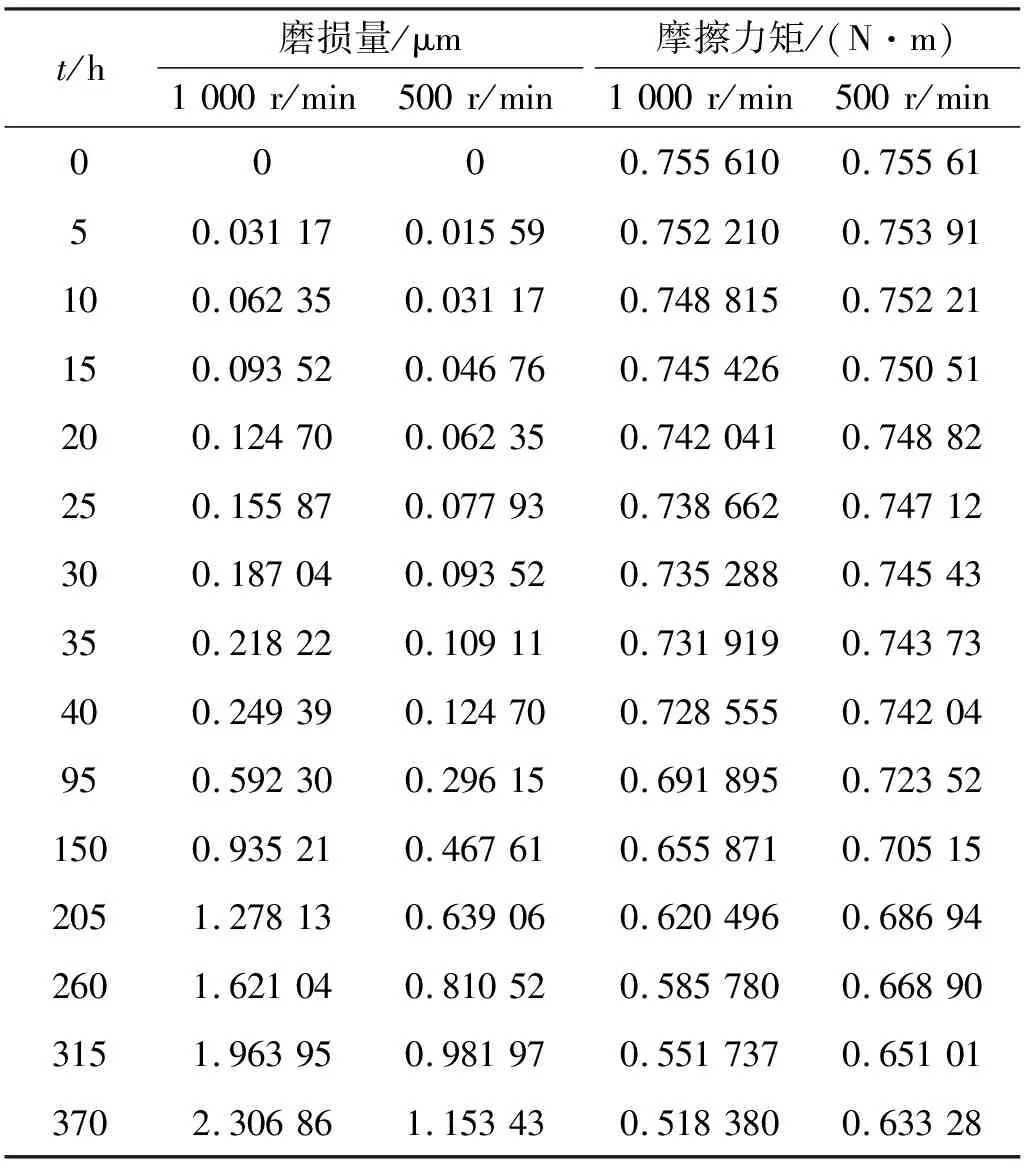
表5 4016型滚珠丝杠副摩擦力矩计算值

图4为4010型和4016型双螺母滚珠丝杠副摩擦力矩的理论变化图，可以看出：①同一型号滚珠丝杠副在不同转速下摩擦力矩变化情况不同，转速越高，摩擦力矩下降越快；②运转相同时间，同一型号滚珠丝杠副在转速1 000 r/min的摩擦力矩下降速度是转速500 r/min时摩擦力矩下降速度的两倍；③在同等转速下，4010型和4016型滚珠丝杠副摩擦力矩下降速度接近一致，4010型丝杠副摩擦力矩下降速度是4016型丝杠副摩擦力矩下降速度的1.04倍，结构参数(4010型丝杠的螺旋角为4.55°，4016型丝杠的螺旋角为7.01°，)会导致摩擦力矩值的大小有差异，但当工况(转速)一致时，对摩擦力矩下降速率的影响并不大。

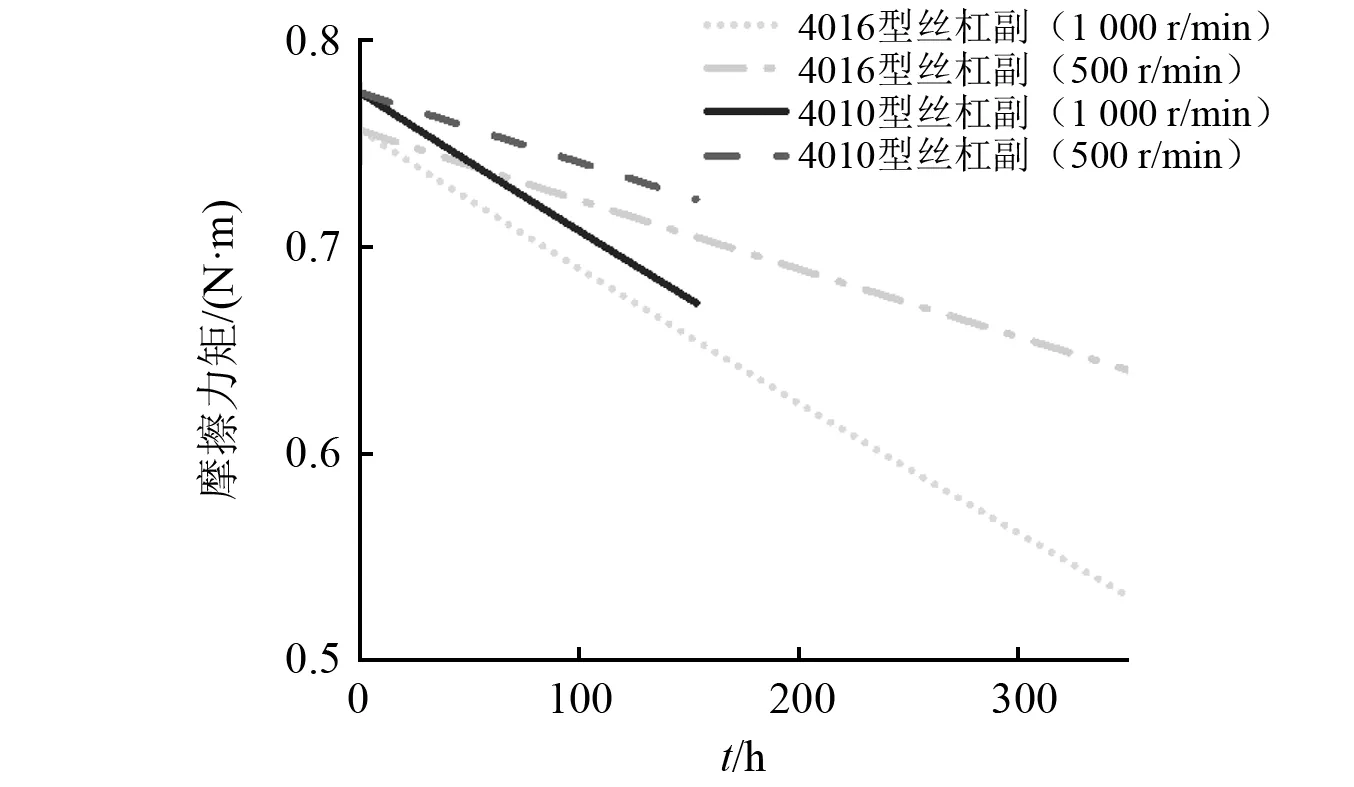
图4 滚珠丝杠副理论摩擦力矩

2 滚珠丝杠副摩擦力矩试验

2.1 试验方法

对4010型和4016型滚珠丝杠副开展滚珠丝杠副摩擦力矩测量试验。其中：①设定检测条件：速度为100 r/min，采样频率20 Hz，根据滚珠丝杠副使用厂家的实际使用工况为脂润滑，且生产厂家所规定润滑条件也是脂润滑，为模拟使用情况下的滚珠丝杠副磨损情况，润滑条件为脂润滑；②在摩擦力矩试验台上安装被测样件，以检测条件所需要的转速进行5 min跑和，使滚珠丝杠副充分润滑；③按照检测条件试验丝杠副的摩擦力矩，当丝杠副完成一次往复运动后停止试验，取丝杠匀速运动时(去除启停加减速阶段力矩测量点)正反向摩擦力矩的检测数据；④连续进行3次检测，取3次检测的平均值作为原始数据。

整体的试验流程如图5所示，首先需将丝杠放在恒温室中充分静置(2 h以上)，使丝杠各部位达到热平衡。其次测量滚珠丝杠副的初始摩擦力矩。最后针对不同的丝杠副设定截尾时间m，并设定采样点n，即在跑和装置上每跑和n小时进行一次摩擦力矩测量试验，当累计时长达到截尾时间mh或出现不可修复故障终止试验。

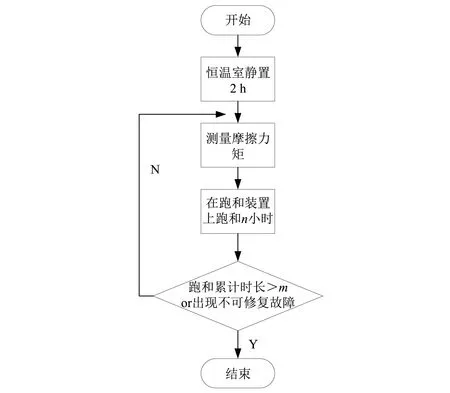
图5 试验流程

2.2 滚珠丝杠副摩擦力矩试验台

滚珠丝杠副摩擦力矩试验台用来测量滚珠丝杠副正反行程的摩擦力矩，如图6所示，测量过程采用一端固定、一端支撑的安装方式，固定端使用三爪卡盘装夹被测丝杠副，支撑端采用顶尖。试验台中部安装可移动的摩擦力矩测量平台，采用直线滑轨进行移动，通过力传感器动态测量被测滚珠丝杠副摩擦力矩。

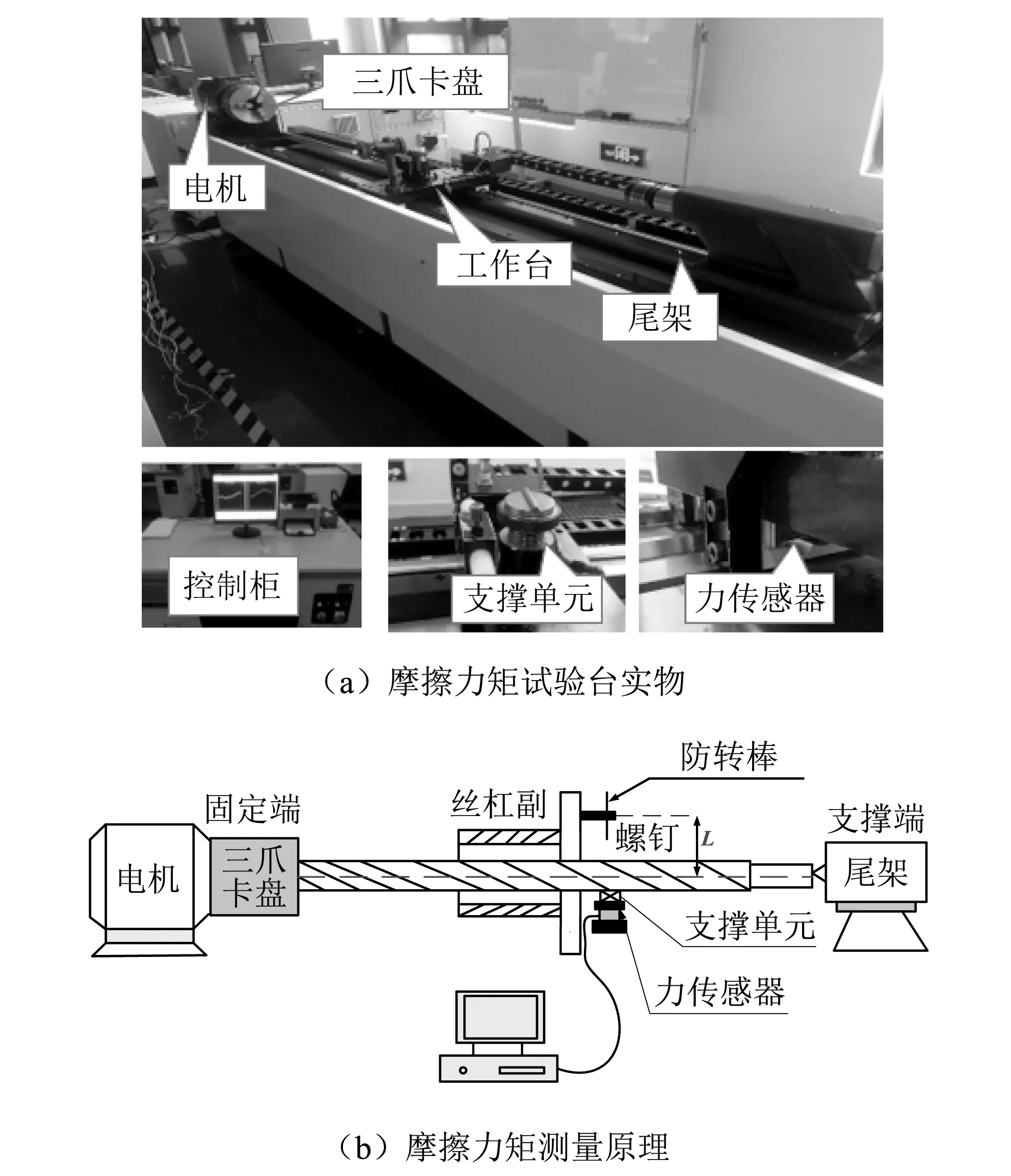
图6 滚珠丝杠副摩擦力矩试验台

测量期间，由于安装在螺母上的螺钉与防转棒接触，防转棒限制螺母的旋转运动，只能带动工作台在丝杠轴向方向运动。在运转过程中，由力传感器测得的圆周运动的摩擦力乘以力臂L即为滚珠丝杠的摩擦扭矩。

3 试验数据分析

3.1 摩擦力矩试验数据

针对厂家A的4010型规格滚珠丝杠副，先在摩擦力矩试验台上对样件进行初始摩擦力矩的测量并记录，其次设定转速1 000 r/min在滚珠丝杠副跑和装置上进行跑和(行程600 mm)，每跑和17 h后将样件从跑和装置中取出，并在摩擦力矩试验台上进行摩擦力矩试验；直至跑和153 h，或出现不可修复故障，终止试验。测量数据如表6所示。

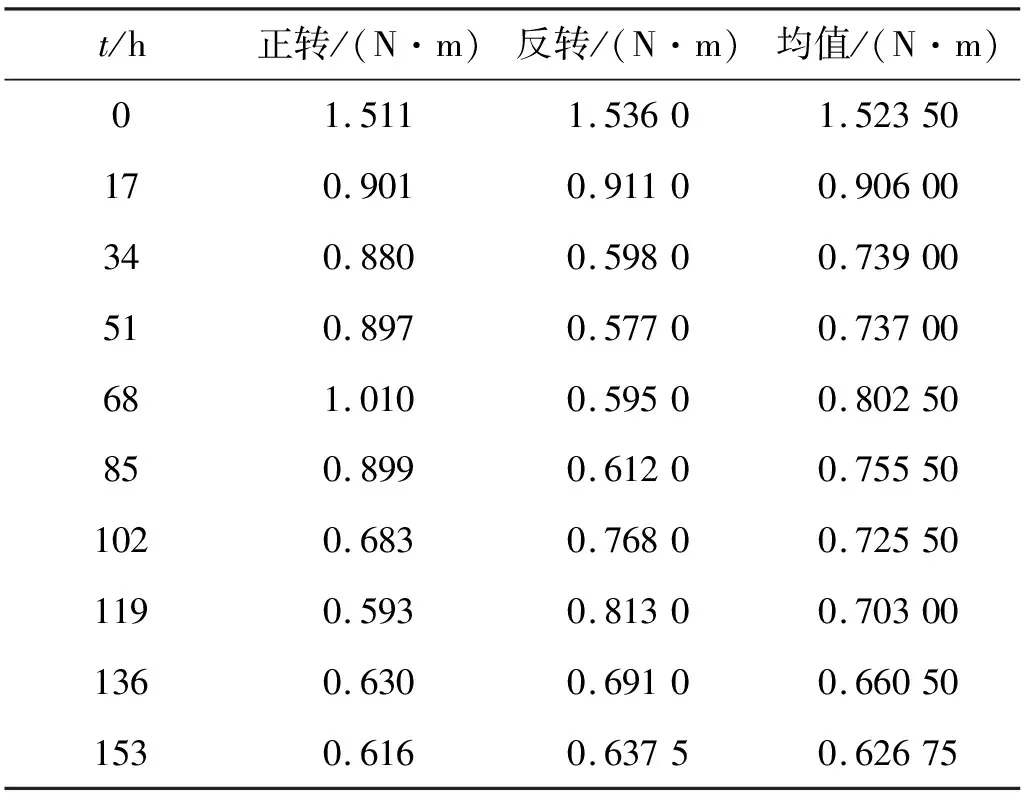
表6 A厂家4010型丝杠副摩擦力矩试验值

针对A、B、C厂家的4016型滚珠丝杠副，应先测量被测丝杠副的初始摩擦力矩值，在丝杠副跑和装置上设定转速500 r/min进行跑和(行程600 mm)，每跑和5 h后将样件从跑和装置中取出，并在摩擦力矩试验台上进行摩擦力矩试验，直至跑和至40 h；40 h以后每跑和55 h取出样件进行摩擦力矩测量试验，直至跑和至370 h，或出现不可修复故障，终止试验。测量数据如表7所示。

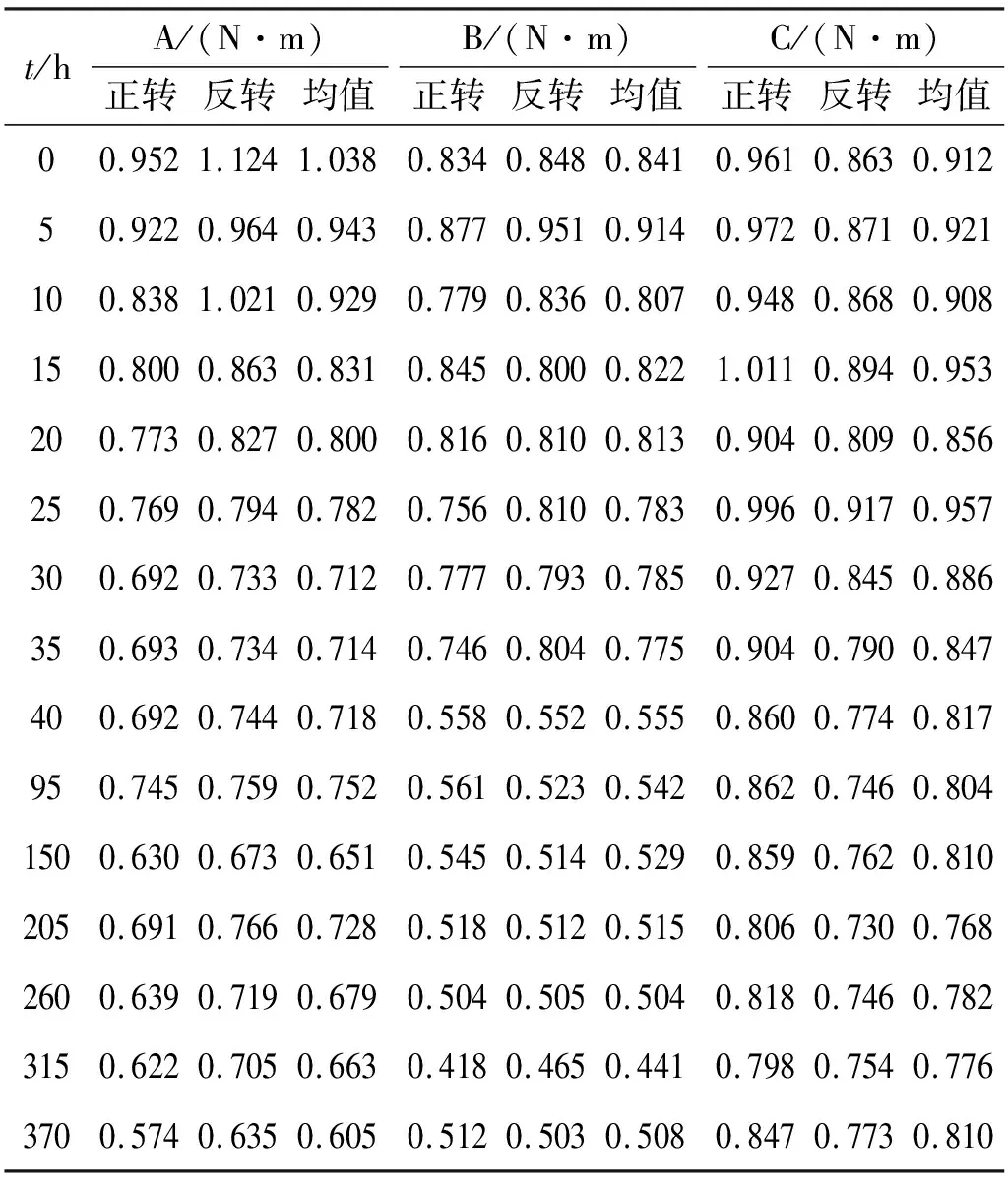
表7 A、B、C厂家4016摩擦力矩试验值

图7为4010型和4016型滚珠丝杠副实测摩擦力矩曲线，可以看出，四个产品的摩擦力矩试验值变化情况存在共同趋势：滚珠丝杠副摩擦力矩均随着时间增加而逐渐减小，且明显存在两个不同的下降阶段，因为丝杠副在运转初始时是处于磨合磨损阶段，丝杠副的形貌并不是完全一致的，这就导致内部受力不完全一致，磨损比较严重，故摩擦力矩下降较快；而运转过一段时候后，滚珠丝杠副处于稳定磨损阶段，内部载荷受力相对均匀，磨损相对较平稳，摩擦力矩下降较慢。所以可以根据摩擦力矩下降情况来反映滚道的磨损，当滚珠丝杠副摩擦力矩下降速度大时表明滚道的磨损严重，而丝杠副摩擦力矩下降速度小时则表明滚道磨损相对稳定。

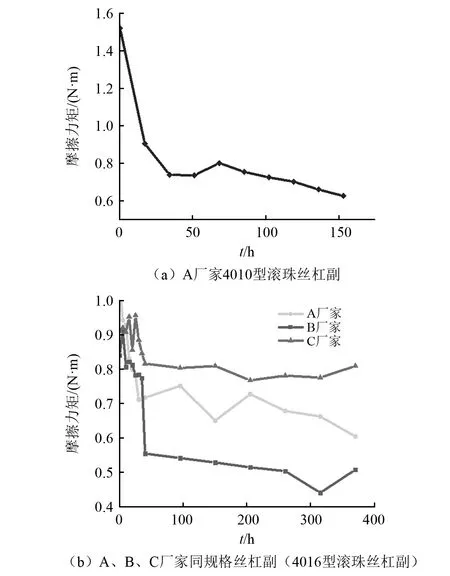
图7 摩擦力矩试验曲线图

3.2 摩擦力矩试验与理论对比分析

将稳定磨损阶段摩擦力矩试验值与理论值进行比较验证摩擦力矩计算公式的正确性。对A厂家不同规格的两个产品在稳定磨损阶段的实测值拟合，并与摩擦力矩计算值比较，如图8、表8所示。

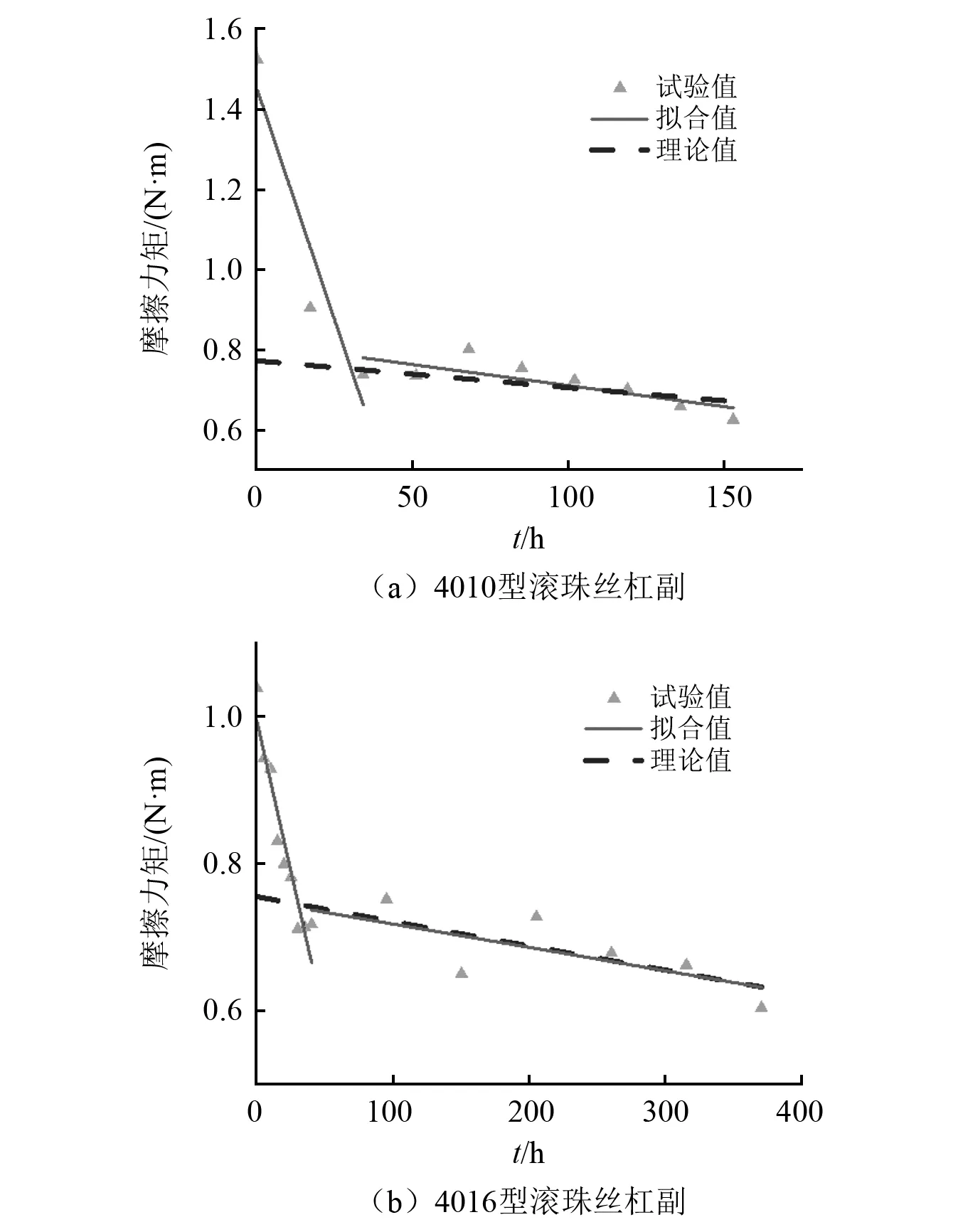
图8 A厂家4010型和4016型样件摩擦力矩实测值与理论值对比

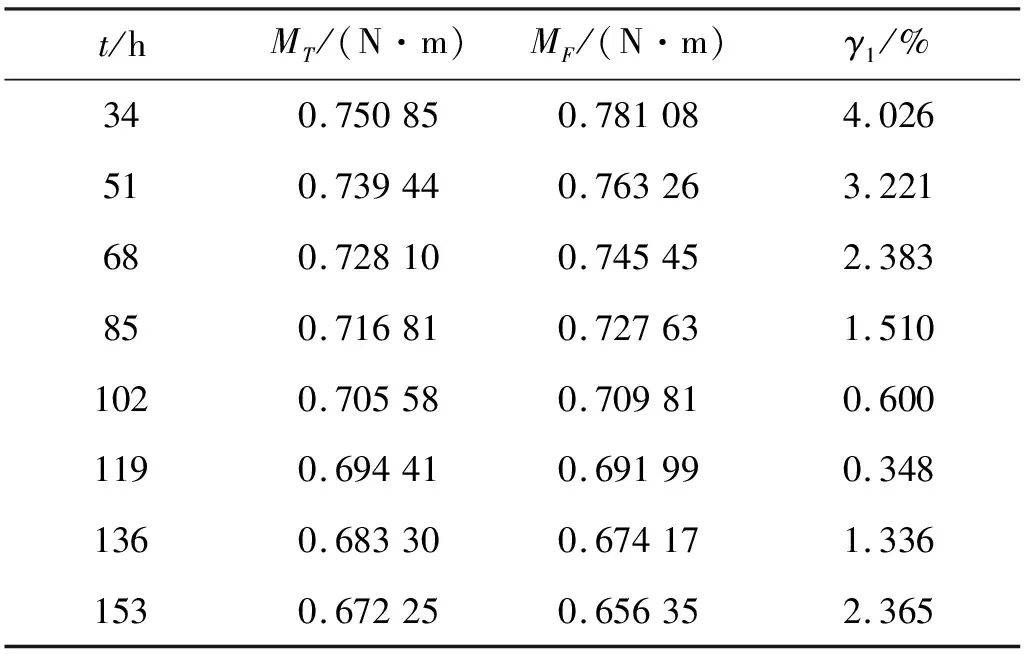
表8 A厂家4010型滚珠丝杠副摩擦力矩理论与试验值误差

图8(a)表明稳定磨损阶段4010型样件的拟合曲线和理论曲线整体走势比较一致，两条曲线在测量时间点下的数值是接近的，如表8所示，MF为基于摩擦力矩试验值拟合的结果；MT为摩擦力矩理论值；γ1为试验与理论的相对误差，可以发现A厂家4010型样件摩擦力矩试验与理论值相对误差在4.026%内，误差较小。

根据图8(b)可以发现稳定磨损阶段4016型样件的拟合曲线与理论曲线几乎完全重合。从表9可知，试验值拟合后，滚珠丝杠副摩擦力矩试验与理论值的相对误差极小，在0.606%以内。

对比表8、表9，可以发现：①4010型和4016型滚珠丝杠副试验与理论值的拟合值相对误差很小，摩擦力矩计算公式吻合度较高，误差在4.026%内；②采样点对于摩擦力矩理论计算值与试验值的的吻合程度有着重要的影响。4016型丝杠副(40 h之前每跑和5 h测量摩擦力矩，40 h后每跑和55 h后测量摩擦力矩)摩擦力矩试验与理论值的差异明显比4010型丝杠副(每跑和17 h测量一次摩擦力矩)小。

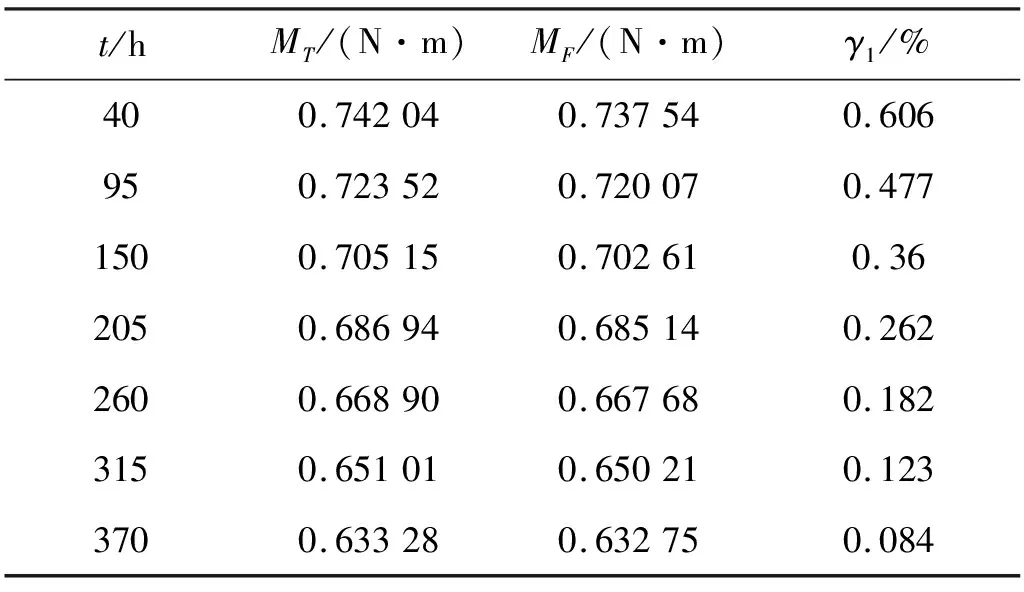
表9 A厂家4016型滚珠丝杠副摩擦力矩理论与试验值误差

A、B、C厂家的被测样件(4016型)的基本参数一致，对三个厂家样件摩擦力矩试验值进行拟合，将拟合值与1.3节中4016型滚珠丝杠副摩擦力矩理论计算值进行比较，以进一步验证摩擦力矩计算公式的准确性。图9为A、B、C厂家4016型滚珠丝杠副摩擦力矩试验与理论的对比图。其中虚线表示理论摩擦力矩，实线表示3家厂家摩擦力矩拟合值。在稳定磨损阶段，摩擦力矩拟合值与理论值趋势一致，变化规律一致，基本吻合。

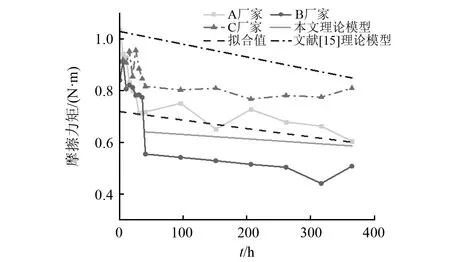
图9 A、B、C厂家的4016滚珠丝杠副试验与理论对比

由表10可知，稳定磨损阶段，拐点40 h时，误差相对而言较大，达到5.803%以上，这是因为3件样件由于厂家的加工误差并非同时进入稳定磨损阶段，误差略大；而从95 h以后，试验样件均已进入稳定磨损阶段，3家样件试验与理论值的相对误差小于4.976%。A厂家4010型滚珠丝杠副摩擦力矩试验与理论相对误差4.026%，4016型滚珠丝杠副摩擦力矩试验与理论值的相对误差在0.606%以内；而A、B、C三个厂家样件的摩擦力矩试验值与理论值的相对误差小于4.976%。A厂家样件的相对误差相对于三个厂家4.976%而言较小，然而单个A厂家相对于三个厂家而言并不具有普适性，行业内各个厂家的加工工艺有差别会导致同一型号的滚珠丝杠副摩擦力矩试验值与理论值的差异不一致，因此，本文摩擦力矩计算公式的误差确定为三个厂家样件的摩擦力矩试验值与理论值的相对误差4.976%。结合图9,可知相比束方婷等提出的滚珠丝杠副摩擦力矩理论计算模型，本文建立的摩擦力矩模型理论值更贴近试验值，误差更小，验证摩擦力矩计算公式的准确性。

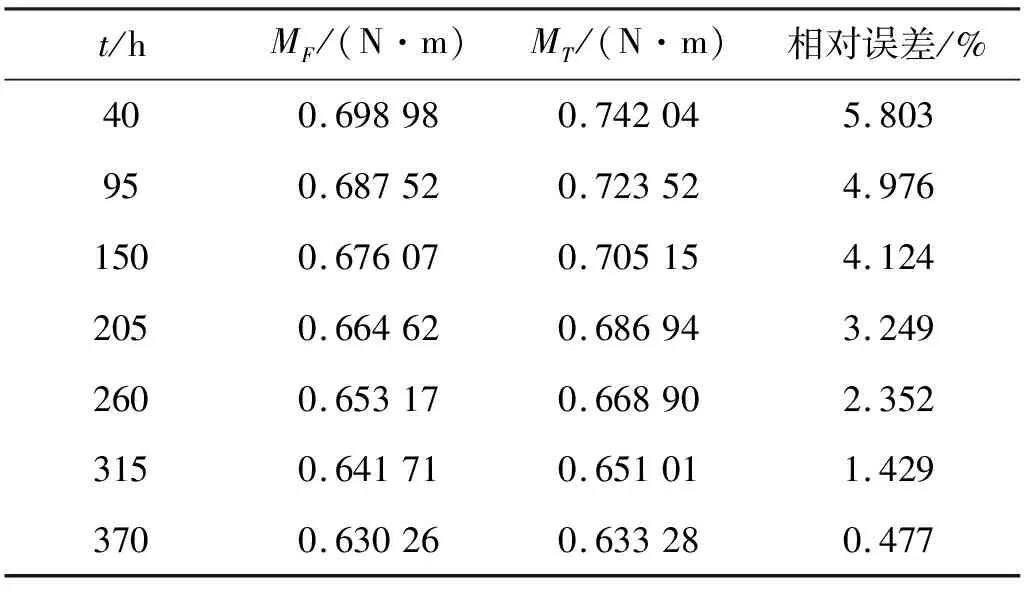
表10 3家产品的摩擦力矩的相对误差

依据图10，随着运行时间的增加，本文提出的滚珠丝杠副摩擦力矩理论计算值与试验的误差越来越小，这是因为滚珠丝杠副在运行过程中，随着跑和时间的增加，滚动体承载会越来越均匀。

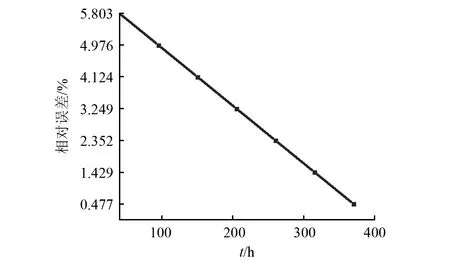
图10 A、B、C厂家4016型样件摩擦力矩误差趋势

4 结 论

基于滚珠丝杠副磨损量的计算，推导了能够反映滚道磨损的摩擦力矩的计算公式，以4010型和4016型双螺母滚珠丝杠副为例，计算两个样件的摩擦力矩并进行理论分析。其次对同厂家的两种不同规格的样件(4010型和4016型滚珠丝杠副)进行试验验证，再以试验的4016型样件为参考，选择不同厂家的4016型产品进行摩擦力矩试验。试验结果表明：

(1)稳定磨损阶段下，建立的滚珠丝杠副摩擦力矩计算公式与试验结果的误差在4.976%以内，相比束方婷等提出的摩擦力矩计算模型，误差更小，验证了本文摩擦力矩计算公式的准确性。

(2)随着运转时间增加，滚动体承载会越来越均匀，试验值与计算值相对误差越来越小，摩擦力矩计算公式的精确性逐步提高，进一步表明计算公式的实用性。

(3)摩擦力矩能够反映滚珠丝杠副的磨损情况——当滚珠丝杠副摩擦力矩下降速度大时表明滚道的磨损严重；而当滚珠丝杠副摩擦力矩下降速度小时则表明滚道磨损相对稳定。现阶段行业内未形成统一的磨损量测量方法与测量标准，本文建立的摩擦力矩与磨损量的关系式为磨损量的测量提供一个新的方法，通过测量滚珠丝杠副的摩擦力矩，结合本文提出的摩擦力矩与磨损量关系式间接实现磨损量的测量。