考虑内力状态的连续刚构桥典型施工阶段地震易损性分析

2022-01-04熊利军郑国足裴银海

振动与冲击 2021年24期

石岩，熊利军，李军，郑国足，裴银海

(兰州理工大学土木工程学院，兰州 730050)

近年来，随着我国西部交通网络的发展，跨越复杂地形、峡谷与河流等的桥梁比重日益增加，其中连续刚构桥以其良好的连续性和受力合理等优势而得以广泛应用[1-2]。但西部山区活动断层与断裂带发育广泛且地震活动强烈，地震灾害对该地区桥梁结构的安全性能具有较高的威胁性[3-4]。如2008年汶川大地震中庙子坪特大桥主桥和引桥均发生了严重损伤，且震后产生了巨大的修复费用[5-6]。连续刚构桥多采用悬臂浇筑法，施工周期普遍较长，主桥内力状态随结构自质量、预应力和施工荷载的逐步施加不断变化，使得该类桥梁结构的受力体系有别于简支梁桥与连续梁桥等桥型。因此，连续刚构桥在不同施工阶段主桥内力状态的改变可能会影响其抗震性能的评估[7-8]。

地震易损性分析作为一种基于概率的结构抗震性能评估方法，以其能清晰反映结构在不同性能水平下的损伤概率与地震动强度之间关系的特点而广泛应用于桥梁结构抗震性能的评估[9-11]。国内外学者已对简支梁桥、连续梁桥、斜拉桥等桥梁的地震易损性进行了大量研究[12-17]。在连续刚构桥易损性分析方面，江辉等[18]基于增量动力分析法分析了连续刚构桥深水环境和地震损伤特性的相关性，认为深水环境会显著增大连续刚构桥的地震损伤概率；谷音等[19]分别以应变和位移作为桥墩和支座的损伤指标对高墩大跨连续刚构桥的抗震性能进行了易损性评估；陈志伟等[20]探究了行波效应对大跨连续刚构桥地震易损性的影响，认为行波效应会增大桥墩的损伤概率，且对高墩的影响要显著大于低墩；张智等[21]分析了墩高及斜交角的改变对斜交连续刚构桥地震易损性的影响，结果表明对于不等高的斜交刚构桥，矮墩发生损伤的概率更大，且钝角处矮墩的损伤概率随斜交角的增大而增大。然而，现有关于连续刚构桥地震易损性的研究主要集中在特殊环境、不同地震动特性和桥墩构造形式对易损性的影响，以及新损伤评价指标探究等方面，对于如何考虑不同施工阶段连续刚构桥内力状态的改变以及刚构桥在不同施工阶段的地震损伤概率的研究较少。

鉴于此，本文针对内力状态对连续刚构桥在不同施工期间地震易损性的影响进行研究。首先以5个典型施工阶段为对象，采用MIDAS/Civil对其进行施工阶段分析并得到其内力状态，基于等效荷载法提出连续刚构桥在施工期间主梁和主墩的内力等效荷载计算公式，并通过OpenSees建立各典型施工阶段考虑与不考虑等效内力状态的动力分析模型；然后以曲率延性系数为损伤指标，通过输入近断层地震动进行增量动力分析，得到主墩墩底、墩顶和主梁根部截面的易损性曲线；最后，分析了考虑内力状态与否对各典型施工阶段地震易损性的影响。

1 典型施工阶段模型及内力状态

为分析考虑内力状态的连续刚构桥在施工期间经受近断层地震动时的地震损伤情况，选取5个典型施工阶段为研究对象。典型施工阶段考虑内力状态的情况为将结构自质量、主梁预应力作用和施工荷载以内力等效荷载的形式附加在结构上，不考虑真实内力状态时仅附加结构自质量。

1.1 桥梁概况

工程背景为一座桥梁全长620 m、桥面总宽12 m的大跨高墩连续刚构桥，其中主桥是跨径为(120+220+120)m的3跨连续T型刚构，引桥是跨径为4×40 m的4跨简支T梁，如图1所示。主桥上部结构(主梁)为变截面单箱单室预应力混凝土箱梁，箱梁顶板宽12 m，底板宽8 m，主梁根部截面高12.5 m，跨中截面高3.5 m，其间梁高按2次抛物线变化；引桥上部结构为等截面混凝土T梁，且每跨5片；全桥上部结构均采用C50混凝土。全桥桥墩皆为钢筋混凝土桥墩，其中1#墩和2#墩为双薄壁空心墩，3#墩～6#墩为单薄壁空心墩，采用C40混凝土，配筋率约为3.5%。主桥采用悬臂施工法进行施工，按照先边跨、后中跨的方式进行合龙，合龙梁段通过合龙吊架施工完成，总体施工时间约为460天。每个施工阶段(T构)箱梁均采用对称预应力结构并双向张拉，边跨、中跨及合龙段纵向预应力钢束皆包括顶板束、底板束和腹板束，均采用Strand1860预应力钢绞线。其中，0#～32#施工块共设置188束顶板及144束腹板预应力钢束，跨中及边跨现浇至合龙段分别设置46束和24束底板预应力钢束，跨中合龙段和边跨现浇至合龙段分别设置10束和8束顶板预应力束，全桥共计452束。0#桥台、3#墩墩顶各设置3个盆式橡胶支座，7#桥台、3#墩～6#墩墩顶各设置5个滑板支座。另外，桥台背墙处、相邻梁体间均设置0.05 m伸缩缝。

图1 大跨高墩连续刚构桥的构造形式与截面尺寸(m)

1.2 有限元模型及特征值分析

选取的5个典型施工阶段分别为0#阶段、8#阶段、16#阶段、24#阶段和主梁最大悬臂阶段(32#阶段)。考虑到MIDAS/Civil和OpenSees软件分别在桥梁施工过程模拟和动力时程分析方面各具优势，故采用二者建立各典型施工阶段的动力分析模型。首先，基于MIDAS/Civil软件分别模拟其施工过程，考虑施工过程中结构自质量、预应力及施工荷载等因素的影响，最终建立5个典型施工阶段分析模型，如图2所示。其次，基于OpenSees地震分析平台建立各典型施工阶段的动力分析模型，其中0#阶段和32#阶段的动力分析模型如图3所示，其他阶段与此类同。主梁关键位置(根部塑性铰区：P1～P2)和主墩关键位置(墩顶/底塑性铰区：P3～P6)均采用基于位移的非线性纤维梁柱单元模拟，且纤维截面的混凝土采用Concrete01材料，纵向钢筋采用Steel02材料。假设其他位置处于弹性状态，均采用弹性梁柱单元模拟。考虑桥墩P-Δ效应，桥梁模型的阻尼比取5%，并采用瑞利阻尼。

图2 基于MIDAS/Civil建立的典型施工阶段分析模型

图3 基于OpenSees建立的典型施工阶段动力分析模型

为验证采用MIDAS/Civil和OpenSees分别建立的有限元模型的一致性和合理性，同时为保证动力计算结果的正确性，对两个模型分别进行动力特性分析。前5阶自振周期如表1所示。可见：自振周期的最大误差在5%以内，且此误差主要来源于软件差异，故所建OpenSees模型与MIDAS/Civil模型具有较好的一致性和准确性。

表1 前5阶自振周期对比

1.3 等效荷载及内力状态

连续刚构桥由于其特殊的结构形式和复杂的施工过程，使得主桥(包括主梁和主墩)在各个施工阶段的内力状态(包括弯矩和轴力)发生变化，若不加以考虑，则有可能对其实际地震反应造成影响。为此，通过MIDAS/Civil软件对各典型施工阶段有限元模型分别进行施工阶段分析以得到主梁和主墩的目标内力状态(目标弯矩与目标轴力)，基于等效荷载法对真实内力状态逐一进行分解与等效并提出内力等效荷载计算公式，然后将计算得到的内力等效荷载分别施加于OpenSees动力分析模型，如图4所示，使其处于等效内力状态(等效弯矩与等效轴力)。

图4 典型施工阶段主梁和主墩的内力等效荷载

1.3.1 内力等效荷载

主梁轴力主要由预应力轴压作用引起。从MIDAS/Civil模型中提取主梁各单元的节点轴力，注意除第1个节点和最后1个节点以外，中间每个节点都对应相邻两个单元的j端和i端；将相邻两个单元在同一节点处的轴力作差，即可得到主梁目标轴力的等效荷载，计算公式为

(1)

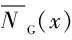
主梁弯矩主要由结构自质量和预应力竖弯作用提供。从MIDAS/Civil模型中提取主梁各节点的质量并计算得到主梁自质量，预应力的竖弯作用以结构自质量的某一倍数反向叠加，即可得到主梁目标弯矩的等效荷载，计算公式为

(2)

图5 各典型施工阶段主梁内力状态所对应的等效荷载

主墩轴力主要由主墩自质量和主梁自质量决定。从MIDAS/Civil模型中提取主墩各节点的质量并计算得到主墩自质量，在附加主梁目标轴力和目标弯矩所对应的等效荷载的基础上，将主墩自质量、主梁自质量和主梁目标弯矩的等效荷载进行叠加，即可得到主墩目标轴力的等效荷载，计算公式为

(3)

主墩弯矩主要取决于主梁轴力，在将上述各等效荷载正确附加到模型上后，主墩的等效弯矩便可基本接近于目标弯矩。

1.3.2 等效内力状态

将上述内力等效荷载对应附加到各典型施工阶段的OpenSees模型上，通过静力分析得到各自的等效内力状态。各典型施工阶段的等效内力状态与目标内力状态的对比，如图6所示。

图6 各典型施工阶段的等效内力状态与目标内力状态对比

可见，各典型施工阶段的等效内力与目标内力基本相等，验证了所给内力等效荷载计算公式的准确性，同时说明基于OpenSees建立的各典型施工阶段的动力模型处于实际内力状态。

2 地震易损性分析方法

2.1 基于IDA的地震易损性

结构的地震易损性，表示在所给某一强度的地震动作用下，结构的地震需求达到或超过某种损伤极限状态的概率，即结构发生某种破坏的超越概率。本文基于理论易损性方法，以加速度峰值(peak ground acceleration，PGA)为地震强度指标，通过增量动力分析法(incremental dynamic analysis, IDA)得到结构在不同地震水平下的响应，然后将结构响应和地震强度指标对数化后进行线性回归分析，得到结构的地震需求概率函数，如式(4)所示；最后，利用式(5)计算得到结构的地震易损性曲线。

lnμ=a+blnIPGA

(4)

(5)

2.2 损伤指标的确定

根据HAZUS99(1999)的规定，桥梁结构或构件在地震作用下的破坏状态共划分为5个等级，分别是：无损伤(no damage，ND)、轻微损伤(slight damage, SD)、中等损伤(moderate damage, MD)、严重损伤(extensive damage, ED)及完全破坏(complete damage, CD)。本文选取曲率延性系数[23]定义典型施工阶段在地震作用下的破坏状态，不同破坏状态及其描述如表2所示[24]。

表2 不同破坏状态的描述及损伤指标

为确定不同破坏状态的界限值，采用OpenSees对各施工阶段不同悬臂长度下的主梁根部截面、主墩墩顶与墩底截面分别进行弯矩-曲率分析。采用马保林[25]的建议，将弯矩-曲率曲线简化为理想弹塑性双线性模型，如图7所示，并从中提取曲率延性指标，即钢筋首次屈服曲率φ′y、等效屈服曲率φy(根据图中两个阴影面积相等求得)、混凝土应变εc=0.004时的曲率φc4及混凝土应变达到极限压应变εcu时的极限曲率φu。不同施工阶段主梁墩底截面的弯矩-曲率，如图8所示。

图7 弯矩-曲率曲线

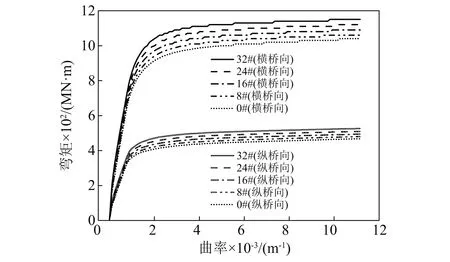
图8 主墩墩底截面的弯矩-曲率

3 地震易损性曲线

3.1 地震动选择及输入

根据Baker为美国太平洋地震工程中心交通设施抗震研究提供的地震动记录数据库，选取场地条件相近、具有速度脉冲效应的40组典型近断层地震动记录作为输入，每组记录包含1个垂直断层走滑方向地震动(SN)、1个平行断层走滑方向地震动(SP)和1个竖向地震动(UP)[26]，各组地震动记录的放大系数谱与平均谱，如图9所示。采用增量动力分析方法进行非线性时程分析，将每组记录中3个地震动分量的加速度峰值以0.10g为增幅从0.10～1.50g进行调幅，共得到1 800条地震动。按照垂直断层走滑方向地震动分量沿纵桥向(X方向)输入、平行断层走滑方向地震动分量沿横桥向(Y方向)输入、竖向地震动沿竖向(Z方向)输入的方式同时输入3个方向的地震动分量进行动力时程计算。分析时各方向各PGA下以40个地震反应峰值的平均值为讨论指标。

图9 地震动记录的放大系数谱

3.2 易损性分析

采用最小二乘法对40组近断层地震动作用下各典型施工阶段主墩墩底、墩顶和主梁根部截面沿纵、横桥向的曲率反应平均值分别进行线性回归，然后通过式(5)求得不同地震水平下的损伤超越概率，即可形成地震易损性曲线。

限于篇幅，图10仅给出了32#，16#和0#典型施工阶段考虑内力状态与否对主墩墩底截面沿纵、横桥向地震易损性曲线的影响。可以看出：不同损伤状态下，各典型施工阶段墩底损伤概率沿横桥向基本都大于纵桥向，这主要是因为各典型施工阶段沿横桥向的结构冗余度与屈服曲率相较于纵桥向更小；无论沿纵桥向还是横桥向，相较于考虑内力状态的情况，不考虑内力状态时墩底截面在不同破坏状态下的易损性曲线均明显降低，即不考虑内力状态时将严重低估其损伤概率。如不考虑内力状态的情况下，PGA为0.4～0.7g时墩底截面沿纵桥向发生轻微破坏和中等破坏的概率较考虑内力状态的情况被低估35%～60%；同一地震动强度下，随着主梁悬臂长度的增加，损伤概率低估量越大。考虑内力状态与否对墩底截面易损性曲线的影响规律沿横桥向与沿纵桥向相同，但不考虑内力状态时横桥向的损伤概率低估量小于纵桥向，且悬臂长度越短，横桥向损伤概率低估量越小。

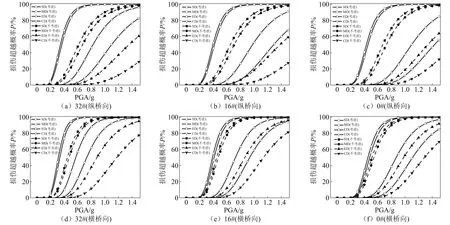
图10 各典型施工阶段考虑内力状态与否对墩底截面纵、横桥向易损性曲线的影响

图11给出了32#，16#和8#典型施工阶段考虑内力状态与否对主墩墩顶截面沿纵桥向地震易损性曲线的影响。可以看出：相较于墩底截面沿纵桥向的易损性曲线，考虑内力状态与否对墩顶截面沿纵桥向的易损性曲线的影响在轻微破坏和中等破坏状态下较大，在严重破坏和完全破坏状态下较小；沿纵桥向不考虑内力状态时将低估各典型施工阶段墩顶截面在不同破坏状态下的损伤概率；在主梁最大悬臂阶段，墩顶截面沿纵桥向发生严重破坏和完全破坏的概率在考虑内力状态和不考虑内力状态这两种情况下基本相等，在其他阶段，PGA>0.8g后易损性曲线因内力状态影响而不同，不考虑内力状态时，墩顶截面的损伤概率被低估，但其损伤概率低估量较墩底截面小。

图11 各典型施工阶段考虑内力状态与否对墩顶截面纵桥向易损性曲线的影响

由于地震作用下0#，8#和16#施工阶段主梁根部截面的竖向曲率反应过小，损伤不足1%，故图12仅给出了24#和32#施工阶段考虑内力状态与否对主梁根部截面竖向地震易损性的影响。

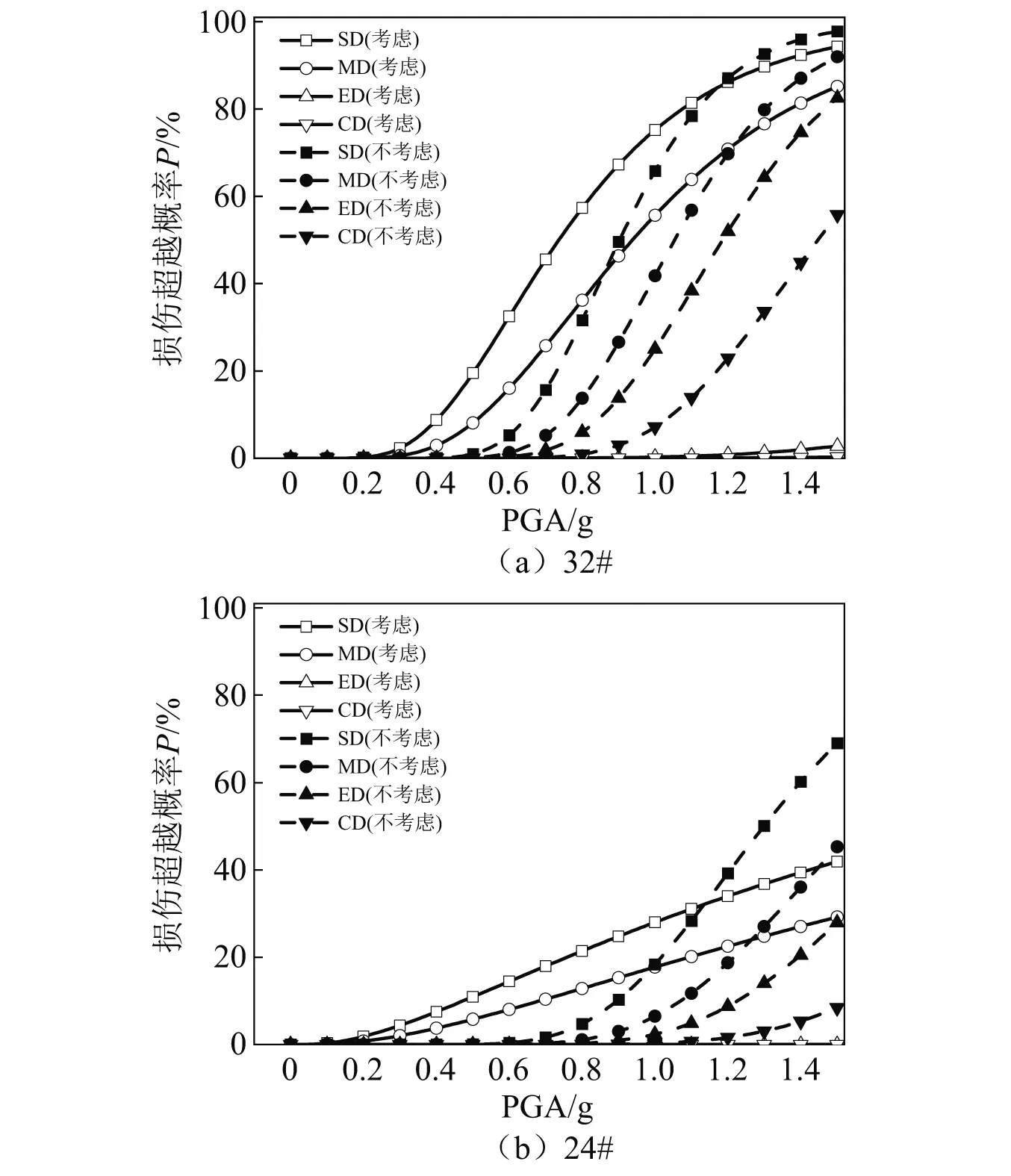
图12 各典型施工阶段考虑内力状态与否对主梁根部截面竖向易损性曲线的影响

可以看出：在轻微破坏与中等破坏状态下，PGA为0.2～1.2g时不考虑内力状态较考虑内力状态的损伤概率小，如PGA=0.8g时32#施工阶段主梁根部截面在不考虑内力状态的情况下发生轻微破坏与中等破坏的概率较考虑内力状态的情况低估约20%；PGA>1.2g后不考虑内力状态较考虑内力状态的损伤概率大。在严重破坏与完全破坏状态下，不考虑内力状态将高估主梁根部截面的竖向易损性，且主梁最大悬臂长度越大，损伤概率高估量也会越大。