航空浮动渐开线花键副轴向载荷分析*

□ 贾继鹏 □ 任工昌 □ 薛向珍

陕西科技大学 机电工程学院 西安 710021

1 分析背景

在航空领域,渐开线花键副相比平键或矩形花键副具有不可替代的优点,被普遍应用于航空发动机及其它动力传递系统中[1]。根据工作状态,航空渐开线花键副可分为固定式和浮动式两种。浮动渐开线花键副在传递转矩的同时,允许一个零件相对另一个零件有一定的角向和轴向位移。这种角向和轴向位移会引起花键副偏角不对中等情况,造成花键副各齿受力不均匀,使浮动渐开线花键副在运行过程中齿面材料和定位圆柱面材料严重磨损,花键副侧隙增大,定位间隙增大,进而使花键副齿间动载荷增大,不对中量增大,非线性振动加剧,花键副工况恶化。工况恶化会进一步加重花键副磨损的程度,如此循环,最终使花键副的寿命及可靠性受到严重影响[2]。对此,进行浮动渐开线花键副轴向载荷分析研究时,需要考虑花键副存在轴向浮动距离,以及花键副轴向不对中与浮动距离复合存在的情况,这对研究浮动渐开线花键副的磨损寿命及可靠性具有重要作用。

目前,国内外诸多学者对航空渐开线花键副进行的研究主要集中在固定式花键副连接不对中、动力学特性,以及花键副连接接触等方面[3-7]。在航空渐开线花键副载荷分布方面,谭援强等[8]对花键副在轴线径向不对中、角向不对中,以及角向与径向不对中复合情况下的载荷分布进行了研究,陈元[9]对花键副径向偏移情况下的载荷分布进行了研究,Cura等[10]分析了径向不对中角度对花键副齿间载荷分布的影响,Cuffaro、Cura等[11]研究了角向不对中量大小与花键副齿键润滑类型对不同形状花键齿微动磨损的影响。对上述研究汇总,研究的对象均为固定式花键副,未考虑浮动距离对花键副的影响,花键副轴向载荷分布的相关研究也主要集中在轴线偏移和内外花键轴线角不对中的固定式花键副,对于具有轴向浮动距离的航空渐开线花键副载荷分布的研究几乎没有,更鲜见同时考虑浮动渐开线花键副轴向浮动距离与偏角不对中对花键副轴向载荷影响的相关研究。

针对航空浮动渐开线花键副在实际工作中存在的轴向浮动、轴向不对中情况,笔者基于Abaqus软件对花键副的轴向载荷进行了分析,并且对花键副单个齿齿顶处、齿根处接触应力和相对滑移距离与不同齿之间接触应力和相对滑移距离进行对比。

2 有限元建模

航空浮动渐开线花键副结构形式如图1所示,航空浮动渐开线花键副在设计时保留一定的浮动距离,在花键副运转过程中,浮动端由于尾轴变形,拉动外花键,使外花键按照一定频率与内花键之间在轴向产生相对浮动。针对航空浮动渐开线花键副进行轴向载荷分析,为花键副的磨损预估建立良好的理论基础。

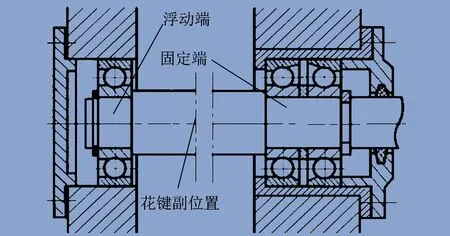
图1 航空浮动渐开线花键副结构形式

航空浮动渐开线花键副设计参数见表1,花键副材料选择18CrNi4A。

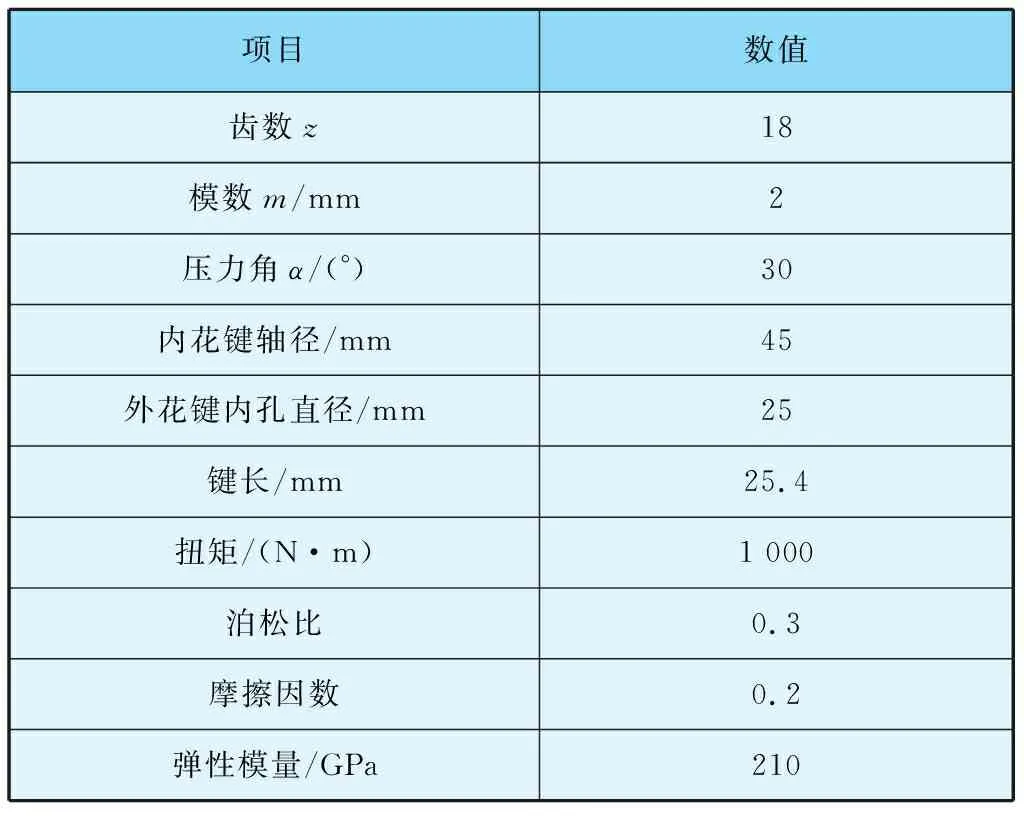
表1 航空浮动渐开线花键副设计参数

根据《机械设计手册》[12],渐开线花键齿廓极坐标参数方程为:

r=R/cosα

(1)

θ=tanα-α

(2)

式中:r为渐开线上某点的向径;R为渐开线基圆半径;θ为渐开线上某点的展角。

渐开线花键副的各直径尺寸为:

Die=m(z-1.5)

(3)

Dii=DFemax+2CF

(4)

Dee=m(z+1)

(5)

Dei=m(z+1.5)

(6)

式中:Die为外花键小径尺寸;Dii为内花键小径尺寸;Dee为外花键大径尺寸;Dei为内花键大径尺寸;CF为齿形裕度;DFemax为外花键渐开线起始圆直径的最大值。

对航空浮动渐开线花键副结构形式进行简化,根据表1及渐开线极坐标参数方程、航空浮动渐开线花键副各直径尺寸公式,在Abaqus软件中建立内、外花键实体模型,然后对模型划分网格。

由于航空浮动渐开线花键副齿形为非规则几何图形,存在许多几何突变位置,因此采用手动划分网格的方式,尽量将整个模型划分为六面体网格单元,这样可以提高计算精度,并提高计算速度。采用六面体八节点位置网格单元,单元类型为C3D8I。

划分网格后的航空浮动渐开线花键副模型如图2所示。根据航空浮动渐开线花键副的实际接触形式,在有限元模型中,将键齿之间设置为面-面接触,将接触行为设置为硬接触,接触算法采用罚函数。根据所用材料的属性,设置摩擦因数为0.2。键齿之间的接触区域为外花键模型中的红色区域,整个航空浮动渐开线花键副有限元模型节点数量为131 072,单元数量为107 674。

图2 航空浮动渐开线花键副模型

为了模拟航空浮动渐开线花键副实际约束条件,对内花键的端面进行固定,在外花键内表面施加1 000 N·m转矩,仅释放Z轴方向的转动和移动,从而使外花键键齿面为主动面,内花键键齿面为从动面。为了方便处理结果,根据花键副轴向不对中角度偏移方向,对每个键齿进行编号,并且对单个齿基于齿高和齿长建立坐标系,齿高为Y轴方向,齿长为X轴方向。

3 浮动距离仿真分析

取内花键X轴正方向浮动距离为0 mm、0.3 mm、0.6 mm、0.9 mm进行仿真计算,得到轴向浮动距离对齿面接触应力影响云图,如图3所示。

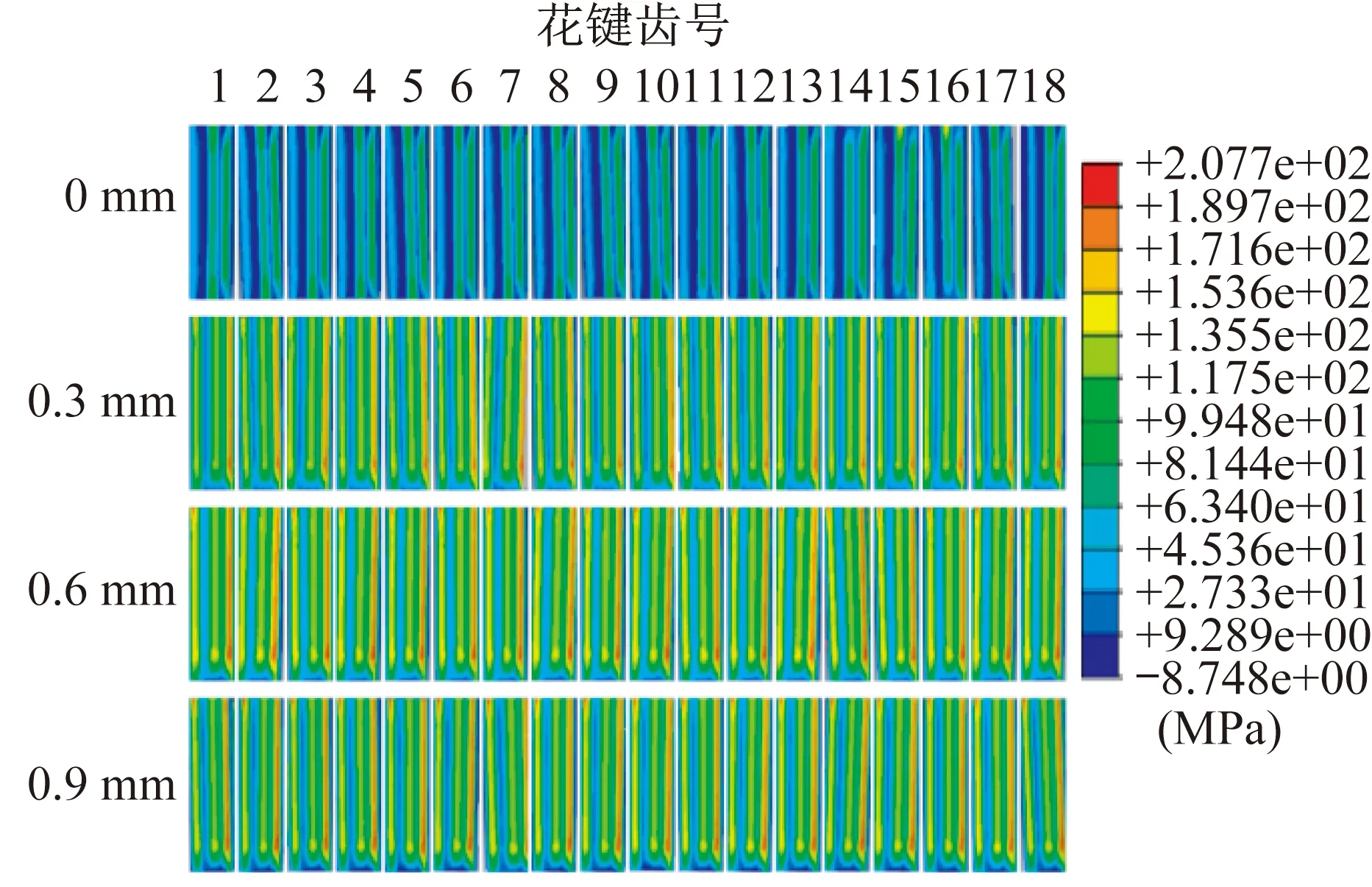
图3 轴向浮动距离对齿面接触应力影响云图

由图3可知,花键副不存在轴向浮动距离时,花键副各齿受力均匀,接触应力沿外花键轴向尺寸分布基本一致,不存在明显应力集中现象。花键副存在轴向浮动距离时,内花键和外花键齿间接触面积减小,外花键齿在齿顶处存在明显应力集中现象。

根据仿真结果,取外花键1号齿齿顶和齿根处计算结果绘制接触应力图,分别如图4、图5所示。

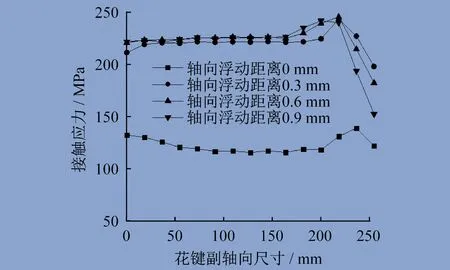
图4 1号齿齿顶接触应力

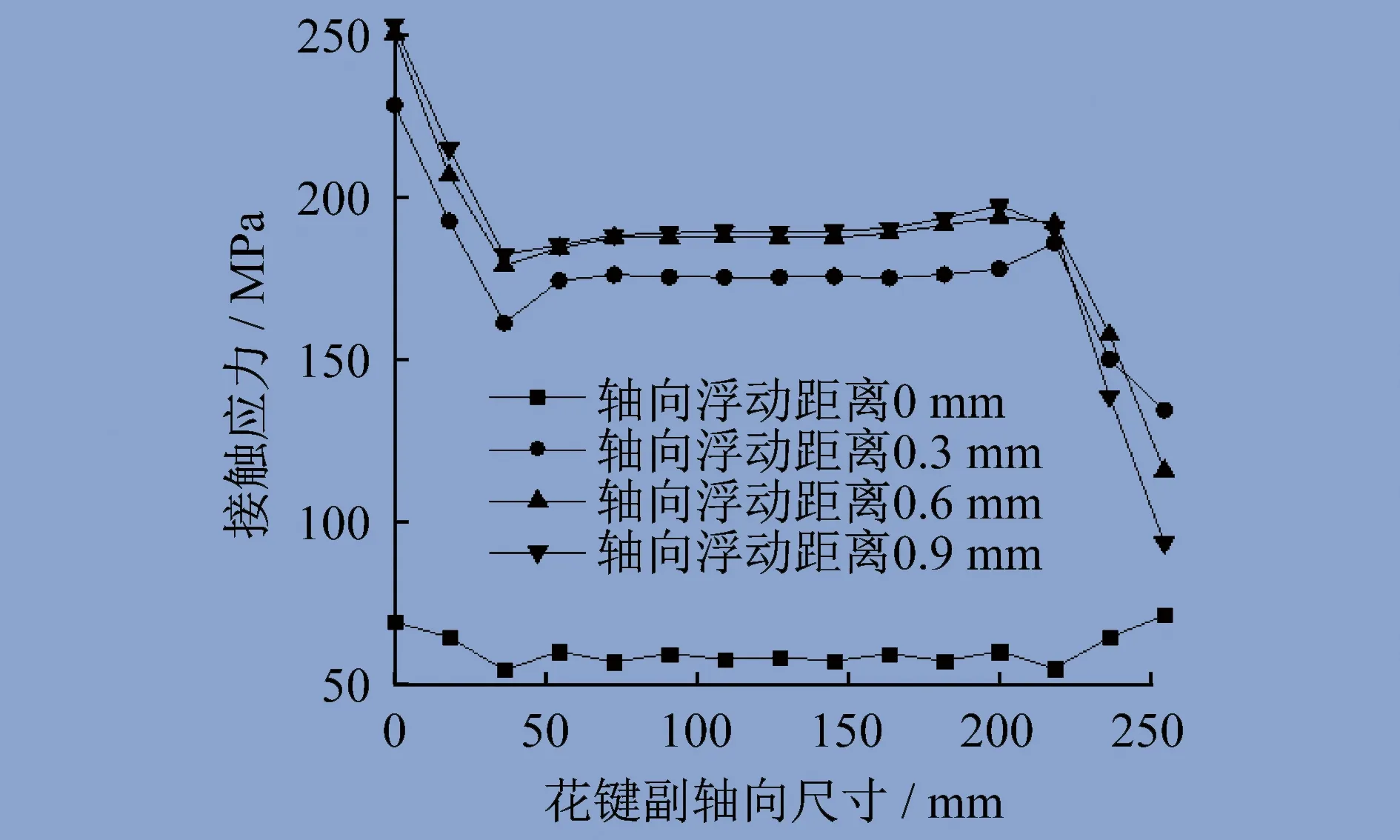
图5 1号齿齿根接触应力

分析齿顶接触应力,当存在轴向浮动距离时,外花键齿顶处接触应力明显增大,在外花键齿顶距右端220 mm处存在明显应力集中现象,随着花键副轴向浮动距离的增大,外花键齿顶右端接触应力分布越来越不均匀。

分析齿根接触应力,当轴向浮动距离为0.9 mm时,接触应力为259 MPa,齿根接触应力相比无轴向浮动距离时明显增大,在外花键齿根左端存在明显应力集中现象。在外花键齿根右端,接触应力明显减小,距右端35～225 mm范围内接触应力分布均匀。随着轴向浮动距离的增大,外花键轴向齿根左端和右端接触应力分布都越来越不均匀。

对比分析齿顶接触应力和齿根接触应力,当存在轴向浮动距离时,左侧轴端外花键齿根接触应力明显大于齿顶接触应力,右侧轴端外花键齿顶和齿根接触应力分布不均匀。

根据仿真计算结果,得到轴向浮动距离对齿面相对滑移距离影响云图,如图6所示。当轴向浮动距离为0 mm时,外花键齿面相对滑移距离分布均匀,齿顶处存在明显的相对滑移。当轴向浮动距离为0.3 mm、0.6 mm时,外花键齿面左端存在较大的相对滑移距离。当轴向浮动距离为0.9 mm时,外花键齿面相对滑移分布明显不均匀,在齿面的左端和中部都存在较大的相对滑移距离。

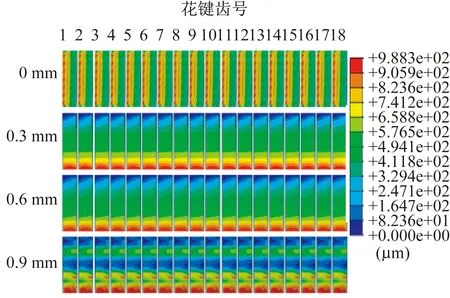
图6 轴向浮动距离对齿面相对滑移距离影响云图

根据仿真结果,取花键副1号齿齿顶和齿根处计算结果,齿顶与齿根相对滑移距离基本相同,绘制相对滑移距离图,如图7所示。当轴向浮动距离为0 mm时,花键副相对滑移距离平均值为0.001 5 mm,内外花键之间仅存在微小的相对滑移距离,根据磨损的基本类型,此时磨损属于微动磨损。当存在轴向浮动距离时,花键副相对滑移距离产生明显变化,相对滑移距离平均值分别为0.298 mm、0.597 mm、0.895 mm,相对滑移距离和轴向浮动距离并不完全相等。产生这一现象的原因是,内外花键之间仍存在微小的径向相对位移,从而引起轴向浮动距离与微小径向相对位移的联合作用。

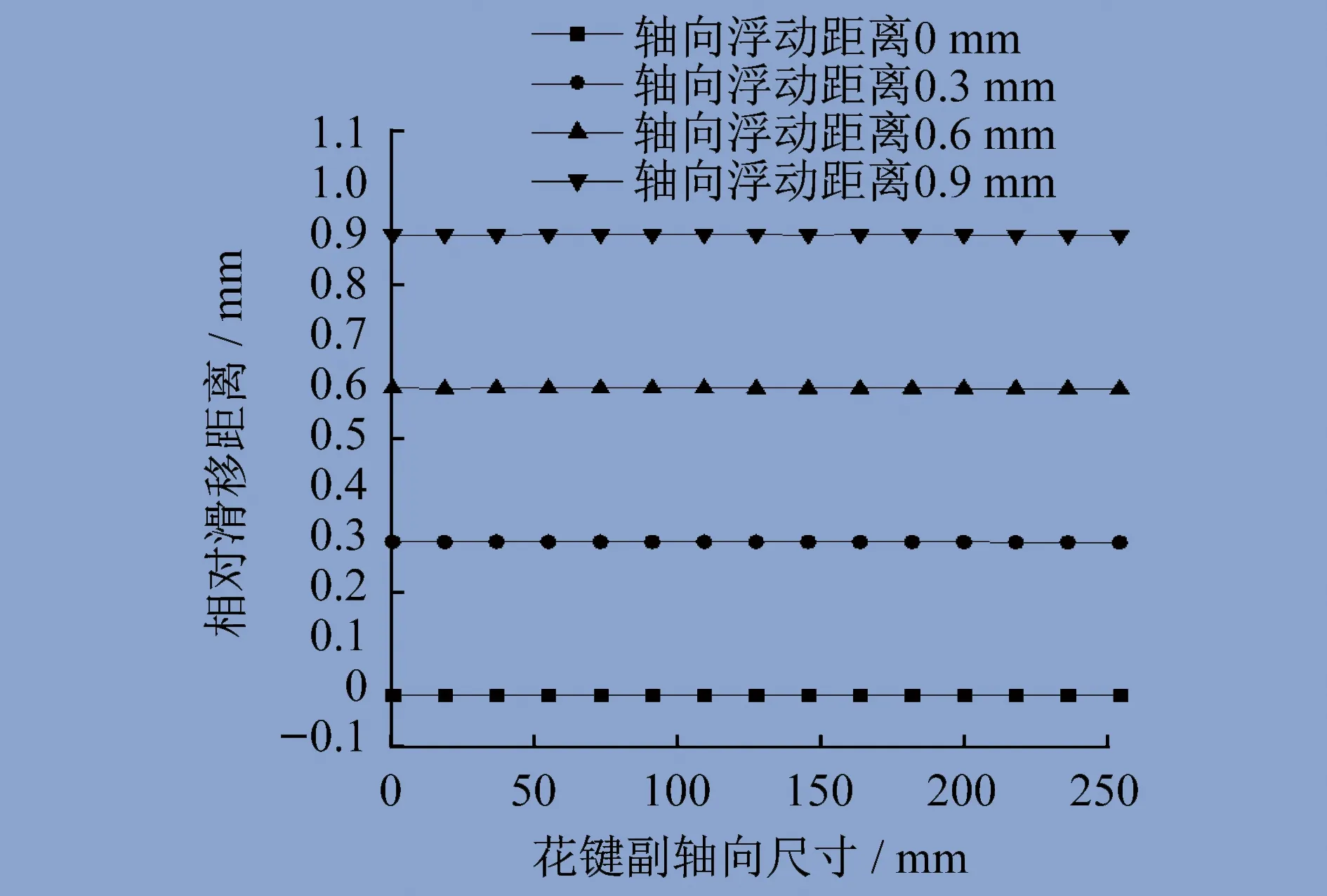
图7 1号齿齿顶、齿根相对滑移距离

4 轴向不对中复合情况分析

对航空浮动渐开线花键副偏载复合情况进行研究。由于复合情况复杂,笔者研究三组复合情况,将航空浮动渐开线花键副轴向浮动距离与轴向不对中角度复合分为三组,见表2。偏移角度方向为X轴正方向。

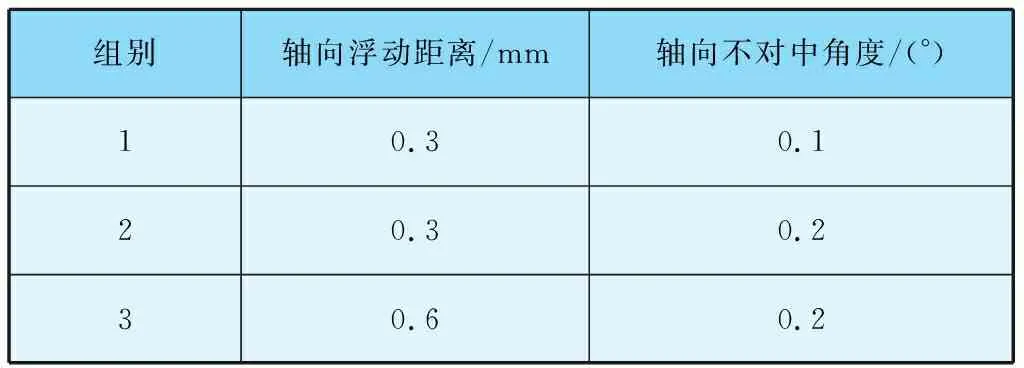
表2 航空浮动渐开线花键副复合情况

三种情况的齿面接触应力仿真云图如图8所示。在相同轴向浮动距离下,轴向不对中角度越大,花键副齿面间接触面积越小。在相同轴向不对中角度下,花键副齿面间接触面积大致相同。

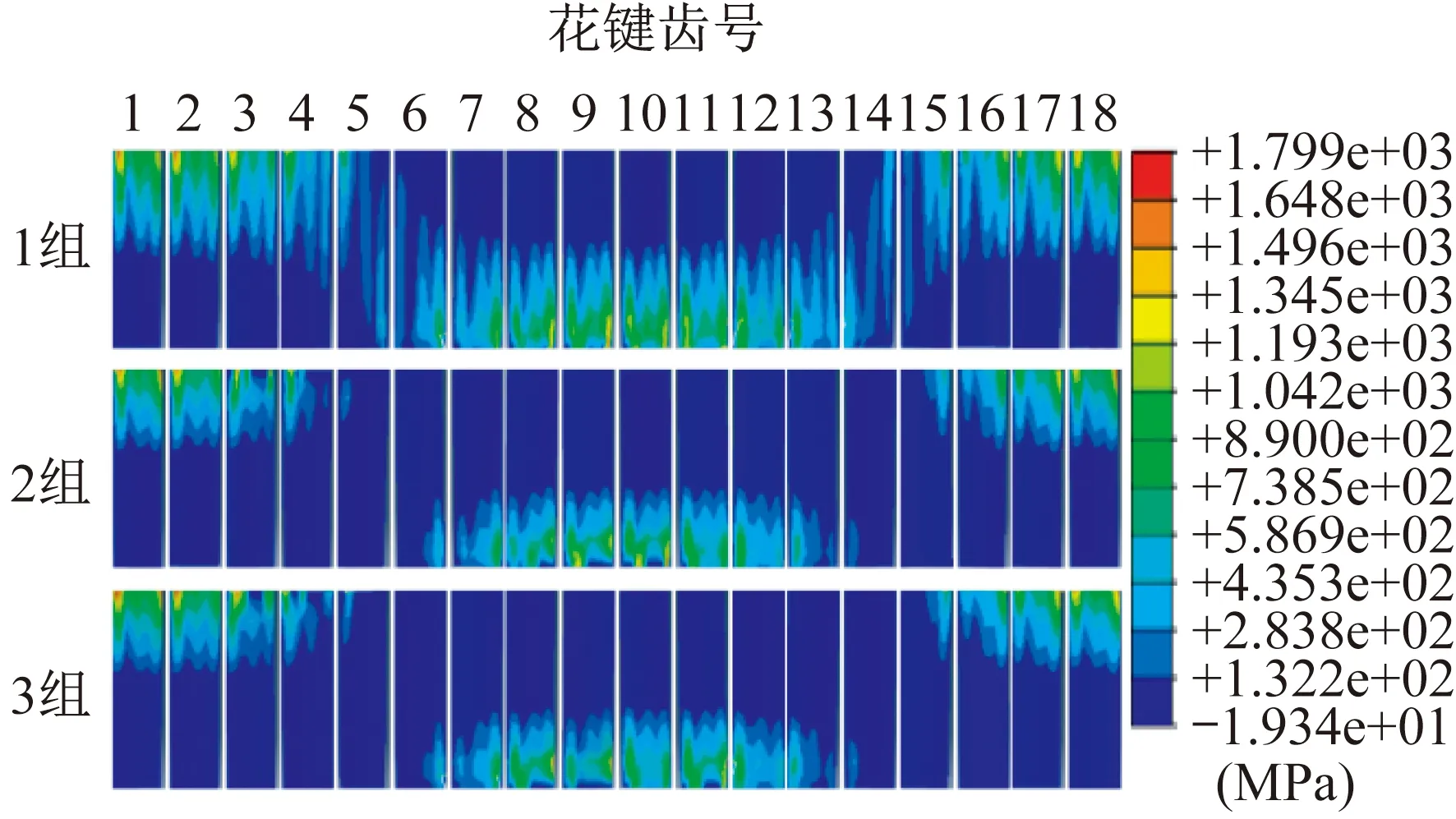
图8 齿面接触应力仿真云图

各键齿最大接触应力如图9所示。在相同轴向浮动距离下,轴向不对中角度对花键副各键齿最大接触应力影响显著,轴向不对中角度越大,齿面最大接触应力越大。在相同轴向不对中角度下,轴向浮动距离对花键副各键齿最大接触应力影响较小,轴向浮动距离越小,齿面接触应力越不均匀,应力集中越明显。

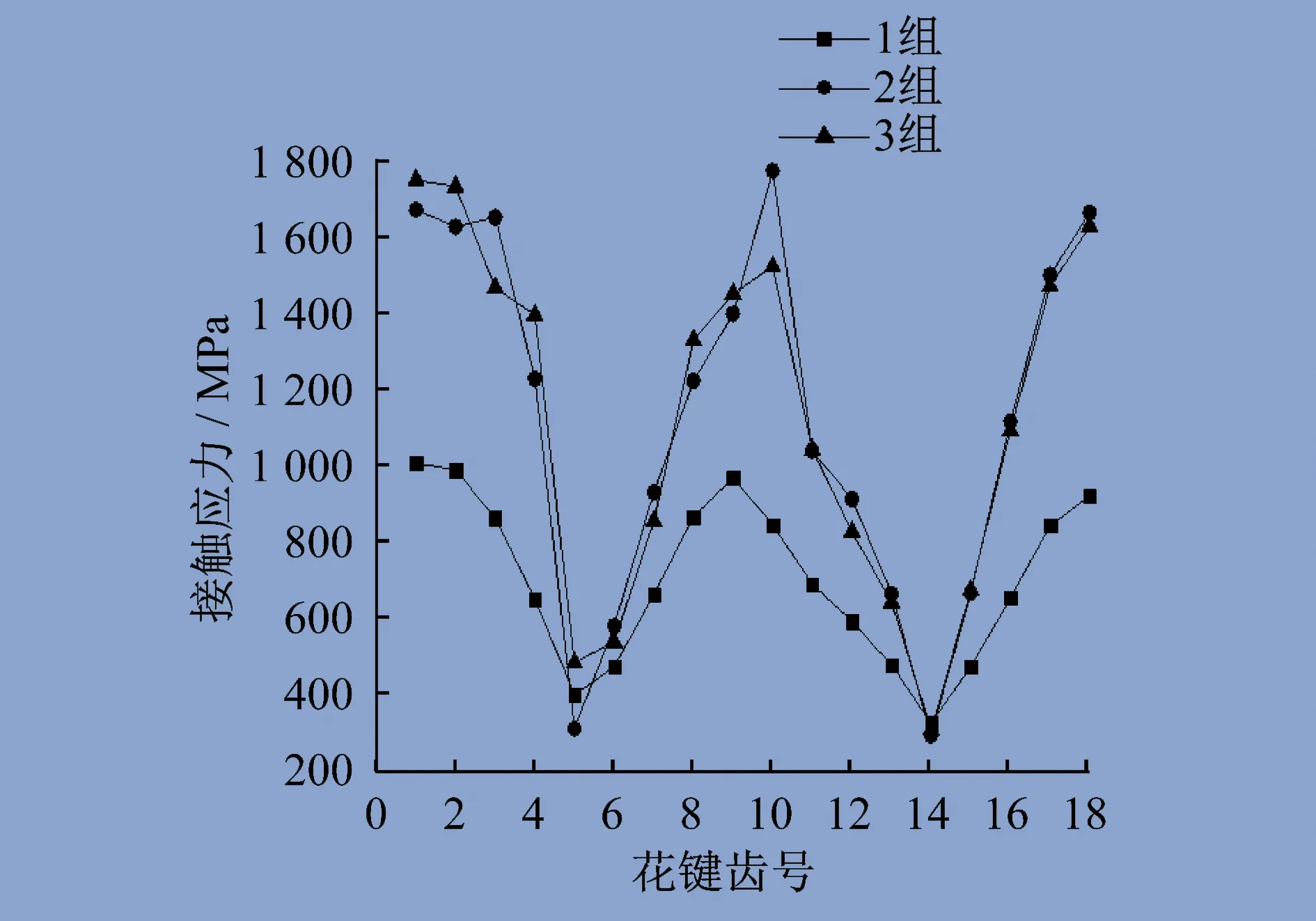
图9 各键齿最大接触应力

取齿面接触面积较大的外花键1号齿和11号齿,1号齿接触应力分布代表外花键左端接触应力分布,11号齿接触应力分布代表外花键右端接触应力分布。分别分析1号齿、11号齿齿顶和齿根接触应力沿轴向分布情况,如图10、图11所示。

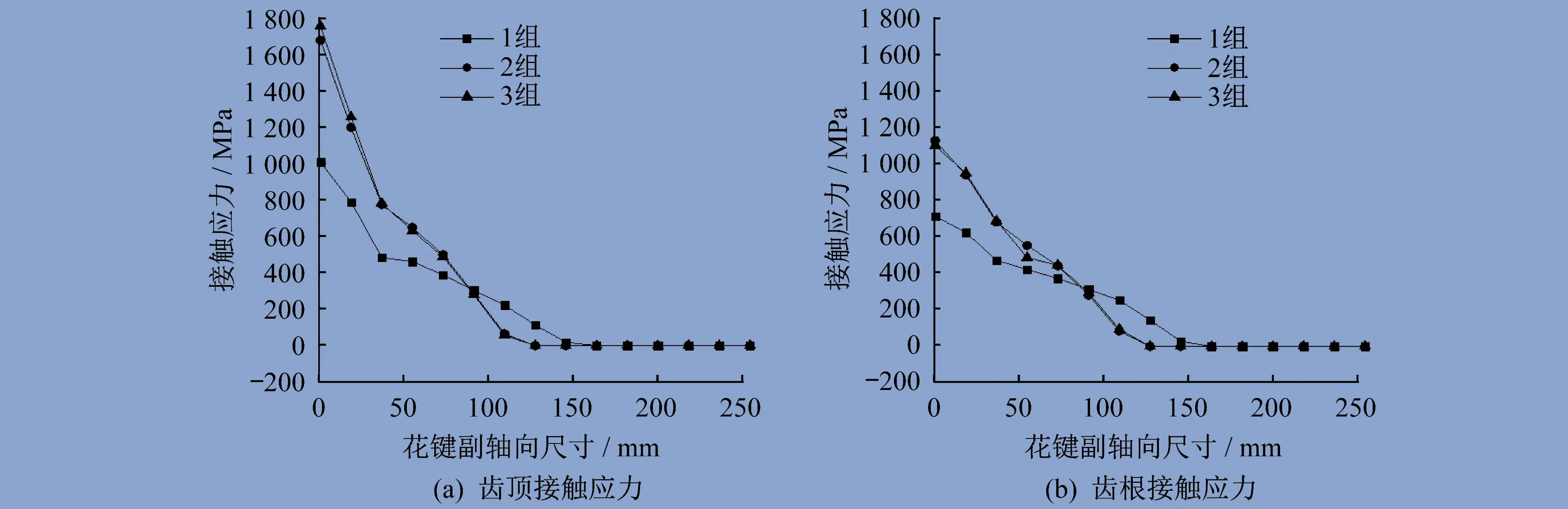
图10 1号齿接触应力沿轴向分布情况

图11 11号齿接触应力沿轴向分布情况

外花键1号齿齿顶和齿根接触应力分布情况大致相同,在相同轴向浮动距离下,轴向不对中角度越大,齿顶和齿根接触应力越大。在1号齿轴向浮动距离和轴向不对中角度复合情况下,轴向浮动距离对接触应力影响较小,轴向不对中在对接触应力的影响中起主要作用。

外花键11号齿齿顶接触应力影响的主要因素仍是轴向不对中角度,在相同轴向浮动距离下,轴向不对中角度越大,齿顶接触应力越大。在相同轴向不对中角度下,轴向浮动距离为0.3 mm时齿顶接触应力为1 776 MPa,轴向浮动距离为0.6 mm时齿顶接触应力为1 523 MPa。轴向浮动距离越小,齿顶右端接触应力越大,应力集中越明显。

外花键11号齿齿根距右端220 mm处存在明显应力集中现象,且在相同轴向浮动距离下,轴向不对中角度越大,齿根接触应力越大,齿面接触应力分布越不均匀。

根据仿真计算结果,得到轴向浮动距离与轴向不对中对齿面相对滑移距离的复合影响云图,如图12所示。在相同轴向浮动距离下,轴向不对中角度越大,花键副齿面相对滑移距离越大,花键副对中性受到的影响越大。在相同轴向不对中角度下,轴向浮动距离越大,对花键副齿面相对滑移距离的影响越大。

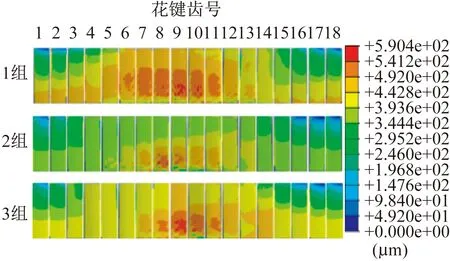
图12 齿面相对滑移距离复合影响云图

根据仿真结果,取花键副1号齿与11号齿齿顶和齿根处计算结果,1号齿与11号齿齿顶和齿根相对滑移距离基本相同,绘制1号齿齿顶相对滑移距离图,如图13所示。在相同轴向浮动距离下,花键副齿面相对滑移距离曲线基本重合,相对滑移距离平均值分别为0.297 mm、0.298 mm,可见轴向不对中角度对花键副齿面相对滑移距离影响较小。在相同轴向不对中角度下,轴向浮动距离越大,花键副齿面相对滑移距离越大。

图13 复合情况1号齿齿顶相对滑移距离

5 结论

通过对航空浮动渐开线花键副进行轴向载荷分析,得到三方面结论。

(1) 花键副存在轴向浮动距离与不存在轴向浮动距离相比,齿面接触应力明显增大。随着轴向浮动距离的增大,齿顶右端接触应力越来越不均匀。外花键齿顶距右端220 mm处存在明显应力集中现象,外花键齿根左端存在应力集中现象。

(2) 在轴向浮动距离和轴向不对中复合情况下,轴向不对中角度在对花键副接触应力分布的影响中起主要作用,外花键齿根距右端220 mm处存在明显应力集中现象。

(3) 轴向浮动距离对花键副齿面相对滑移距离影响显著,并且齿面相对滑移距离和轴向浮动距离并不完全相等。产生这一现象的原因是轴向浮动距离与微小径向相对位移的联合作用。

分析发现轴向浮动距离对花键副齿面接触应力和相对滑移距离影响显著,为设计航空浮动渐开线花键副及进一步研究航空浮动渐开线花键副的磨损提供了良好的理论基础。