基于单分类支持向量机的优势储层评价方法

周雪 张珊珊 李禄胜 李玉蓉 柳伟明 赵晓亮 董鹏

1. 延长油田股份有限公司志丹采油厂；2. 中国石油大学(北京)油气资源与探测国家重点实验室

实际油藏非均质性强，油藏产能主控因素较难确定，因此也造成优势储层难以判别［1］。目前，对于优势储层的评价需要基于地震资料及测井资料等的深入研究［2-4］，以及基于储层岩心实验［5］，难以推广到预测整个油藏中优势储层的平面分布［6］，且不能兼顾井的实际生产情况，导致预测精度较低。

随着算法以及算力的提升，应用机器学习自动进行优势储层判别成为可能。目前，主要以有监督的机器学习算法来进行自动优势储层判别。该方法使用地震数据、测井数据、岩性数据等，通过人工识别出优势储层数据作为样本来训练机器学习模型［1,7-9］。

然而，该方法首先需要人工为数据集标定标签，提高了应用门槛。此外，这些方法一般基于单井剖面进行优势储层评价，无法确定全区的优势储层分布。因此，笔者提出一种基于单分类支持向量机(OCSVM)［10］的全区储层评价方法，该方法所使用的数据为三维地质模型数据体。由于单分类支持向量机属于无监督算法，在实际训练过程中，无需专业人员对地震、测井等数据进行优势储层的标签标定，仅需人为指定出高产井，并使用该井井周的三维地质模型数据作为训练样本。模型训练完成后，即可在全区范围内检测高产区域，为后续井位部署及调整、油藏开发方案设计提供明确的参考标准。

1 基于OCSVM的优质储层评价理论

在实际油田开发过程中，高产井数量较少，如何利用高产井所处的地质信息来寻找出油藏中类似的区域分布对布井及开发有重要现实意义。该问题可看作只有一类样本的新颖性检测问题。将高产井近井地质信息作为正样本，通过检测油藏中是否有类似特点的储层以获得较高的产量。本文使用单类支持向量机对储层的地质信息进行检测，以获得可能为高产区的优质区域平面分布来确定优势储层。OCSVM是一种无监督算法［11］，已广泛用于异常检测及入侵检测领域［12-14］。它学习一个决策函数来进行新颖性检测，将新数据分类为与训练集相似或不同的数据。该算法寻找一个超平面使得正例尽可能远离原点，预测则是用这个超平面做决策，该超平面被称为决策边界。若样本落在决策边界正方向，即认为是正样本，反之为负样本，如图1。

图1 OCSVM分类问题Fig. 1 Classification of OCSVM

OCSVM的目标函数为

为求解该问题，首先引入拉格朗日函数

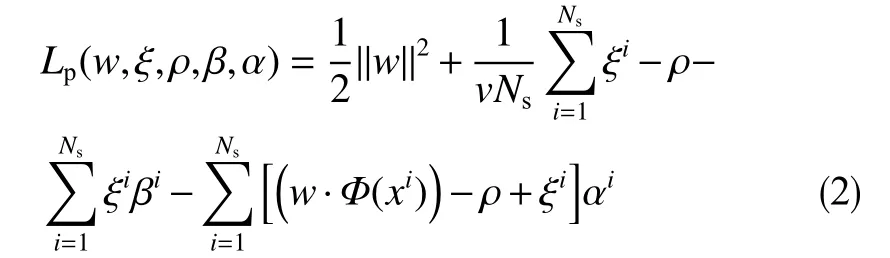
式中，xi为样本数据；v为平衡参数，是一待优化超参数；ξi为松弛变量，用于控制模型的拟合程度，其值越大，模型越倾向于欠拟合；Ns为样本个数； Φ为向特征空间映射的函数；w和 ρ分别为特征空间超平面法向量和偏移量；α ,β为拉格朗日因子。

Φ(x)可 以使用核函数K(xi1,xi2)计算内积

令Lp对w,ξ,ρ的偏导分别为0并代入式 (1)，并将Φ(x)的内积写为核函数形式，可对原问题的对偶形式化简为

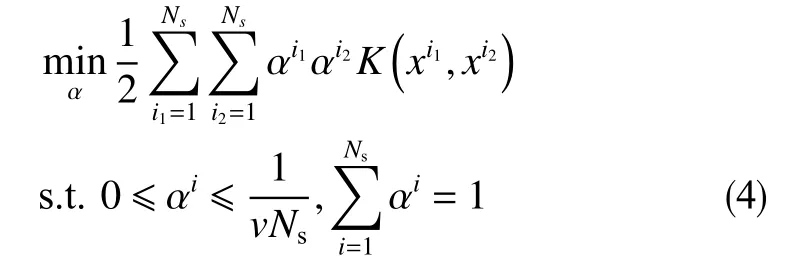
求得α，即可确定OCSVM模型。

由此，可通过决策函数判断样本是否属于正例，如式(5)，

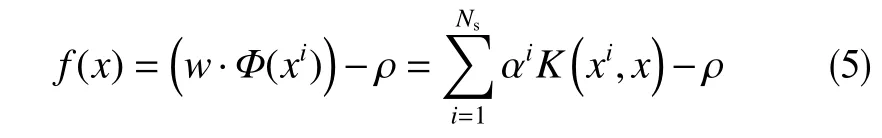
若f(x)＞0，则表示该样本落在决策边界正方向，判定为正例，反之为负例。可以看出，决策函数值表征了样本在投影空间到原点的距离，其值越大，表明该样本越接近正例样本。

本文中，所使用的核函数为高斯核函数，如式(6)。

式中，σ为径向基半径，其值大小表示样本对其他样本的影响程度，为待优化超参数。

2 优质储层评价方法流程

2.1 数据预处理

假设某区块有生产井Ns口，该区小层数Nl层，地质属性特征Nf个，则样本集可表示为

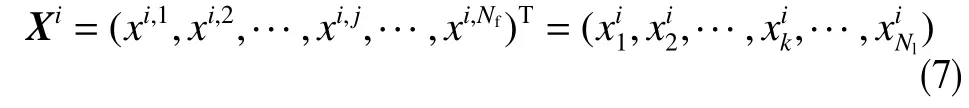
在输入OCSVM模型之前，对样本集数据进行归一化

其中

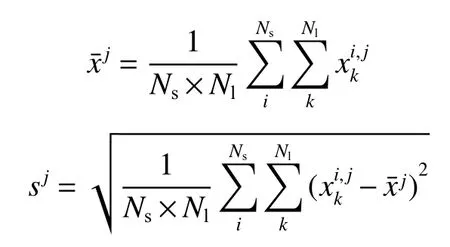
最后，在特征维度按层对样本张量进行拼接后获得二维输入数据

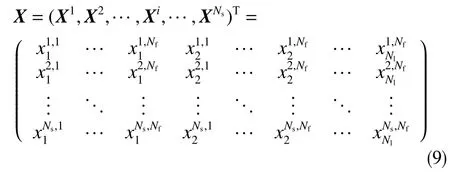
式中，上标i表示第i口井，上标j表示第j个地质属性，下标k表示第k小层。

2.2 模型训练及评价

对于式(4)的优化问题，同时求解出所有 α是较为困难的，因此，Platt提出了序列最小优化算法SMO算法［15］来高效求解式(4)。SMO算法采用了一种启发式的方法，其基本思想是每次选出两个α进行优化并固定其他的 α值。重复此过程，直到达到终止条件即可得到优化结果。

为了评价模型质量并优选模型，构建了决策函数值与产量的相关性系数作为评价指标，如式(10)所示。

式中，f(xi) 为 样本i的决策函数值，(xi)为样本决策函数值的均值，QCi为样本i的累积产量，Q¯Ci为样本平均累积产量。

Cor越接近1，表示决策函数值与累积产量越正相关，这表明随着累积产量的增加，决策函数值将相应地增加，其相关性越强，所训练的模型越能更好地将正样本分离；Cor越接近−1，表示决策函数值与累积产量越负相关，表明模型学习到了错误的特征，无法使得正样本远离投影空间原点；Cor越接近0，表示决策函数值与累积产量越无关。为确定最优模型，可使用相关性系数Cor作为评价指标，对模型超参数，如径向基半径和平衡参数进行优化。通过调整超参数，获得使相关性系数Cor最大的模型作为最优模型，进而对全区地质特征样本的决策函数进行计算来确定优势储层区位，图2为本文中优势储层评价流程。

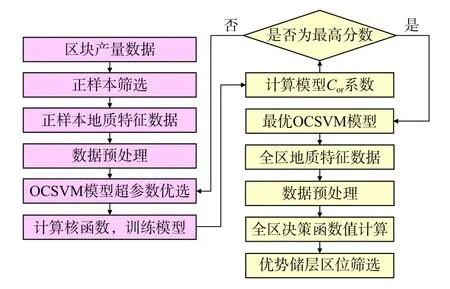
图2 基于单分类支持向量机的优势储层评价流程Fig. 2 Favorable reservoir evaluation process based on OCSVM

3 案例分析

一非均质黑油油藏数值模型如图3所示，模型网格维度为26×26×5。生产井受平面非均质性和纵向非均质性的影响。

图3 案例数值模型Fig. 3 Numerical model of the case

本文选区的地质属性特征为渗透率对数、饱和度和孔隙度，即Nf=3。小层数为5，即Nl=5。每小层的属性如图4所示。生产井20年累积产量如图5所示，可以看出PR1、PR9、PR7产量显著较低，因此将其从样本集中剔除。使用其余井的数据对模型进行训练，即Ns=6。从图5中井周地质特征可以看出，对于非均质储层，仅通过对比地质特征平均值不能有效地筛选出高产区域，应当结合地质属性的分布特征进行综合判断。基于单分类支持向量机的优势储层评价方法，可以对地质属性的分布特征进行有效利用，提高了优势储层判别准确度及速度。

图4 案例数值模型小层地质属性平面分布图Fig. 4 Distribution plane of subzone geological attributes in the numerical model of the case

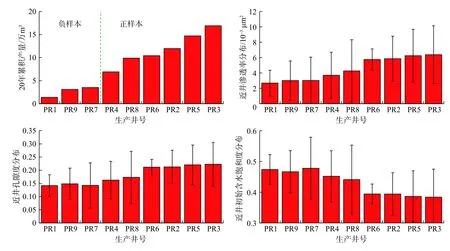
图5 生产井累积产量及近井地质特征分布柱状图Fig. 5 Cumulative production of production well and distribution column of geological characteristics near the well

为了确定最优OCSVM模型以对全区储层进行评价，使用相关性系数Cor作为OCSVM模型得分指标，对模型超参数径向基半径和平衡参数进行优化。由图6可以看出，最优径向基半径为0.01，最优平衡参数为0.1。基于最优OCSVM模型，使用式(5)计算样本的决策函数值后，绘制其与产量的散点图，如图7所示，使用式(10)计算其相关性为0.9764，说明决策函数通过地质信息可以较好地反映产量大小。

图6 OCSVM模型超参数优化结果Fig. 6 Optimization result of super parameters of OCSVM model

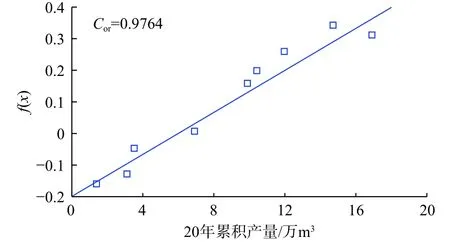
图7 累产量与决策函数关系图Fig. 7 Relationship between cumulative production and decision function

基于训练好的OCSVM模型对整个储层进行评价，将平面上每个网格作为一个样本，因此，该模型一共可产生26×26=676个样本。为每个样本计算决策函数值，并绘制等高线，如图8所示。

图8 决策函数等高线Fig. 8 Contour of decision function

为了进一步测试模型的可靠性，沿模型的对角线选取3个典型样本进行日产量对比，如图9所示，可以看出在决策函数等高线较大的位置，井的产量也较高。表1总结了井点处样本和测试样本的决策函数值。

图9 测试样本日产量图Fig. 9 Daily production of test samples

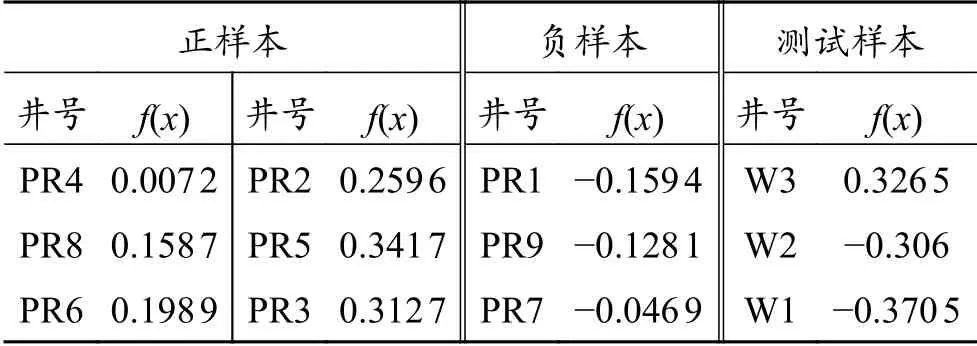
表1 样本的决策函数值Table 1 Decision function value of samples

4 结论

(1)基于高产井的井周地质特征，采用单类支持向量机模型对其学习并使用决策函数来评价全区的地质模型数据，获得优势储层平面展布图。结果表明，展布图与产量有着明显的相关性，证明该评价方法的有效性。

(2)建立了基于单类支持向量机模型的优势储层评价方法，该方法由于无需人为给定标签，使得该方法兼顾了易用性与准确性，为确定全区高产区域分布提供了有力工具。