基于MATLAB松组合导航的仿真实验内容设计和实现＊

符 强，任风华，贾茜子，刘庆华，赵中华，孙安青

（1.桂林电子科技大学信息与通信学院，广西 桂林 541004；2.桂林电子科技大学电子工程与自动化学院，广西 桂林 541004）

导航工程专业是一门融合多学科的新兴工程专业，主要学习导航系统与组合导航技术，可在航空航天领域、交通、军事、电子信息及通讯产业等部门工作。培养的学生既要求有较强的理论知识，又要求具备解决复杂工程问题的能力。

针对当前桂林电子科技大学信息与通信学院导航专业在实验教学过程中内容不够丰富、综合设计性实验项目和自主创新性实验项目不足等问题，联系本专业相关基础、专业理论和社会需求的实际工程问题，设计带有综合性、挑战性和自主创新性的实验项目，并在2016级和2017级学生中开展改革与实践[1-4]。实践表明：该实验项目既加深了学生对GNSS导航、INS导航和松组合导航理论知识的理解，又实现了多门专业课程的融合，培养了学生的创新能力[5-6]。

本文在改革实践的基础上，以基于MATLAB松组合导航仿真实验来讲解综合设计性实验内容的设计和实践。

1 GNSS与INS

全球导航卫星系统（Global Navigation Satellite System，GNSS），具有实时性，它的定位误差不会随着时间增加，缺点是容易受到外界信号的干扰，数据更新频率不高。

惯性导航系统（Inertial Navigation System，INS）具有完全自主、不容易受到干扰、输出信息量大、输出实时性强的明显优点，其缺点是导航精度会随着时间的增加而降低。

从上描述可见，GNSS和INS优缺点互补，如果将GNSS和INS组合在一起，其总体性能会优于各自独立的系统，是理想中的导航系统[5，7-8]。松组合导航系统就是结合GNSS和INS的一种相对简单的组合方式，在该方式下，GNSS和INS独立工作，但将两者的数据进行融合后可以修正INS系统的相关参数，进而给出较好的导航估计结果。

2 基于MATLAB松组合导航实验设计与实现

GNSS/INS松组合的结构如图1所示，其中GNSS接收机和INS分别独立工作。松组合利用GNSS接收机输出的位置和速度信息和INS经过力学编排后输出的位置和速度信息进行组合，两者共用一个GNSS/INS组合滤波器，双方进行数据融合后得到输出的位置、速度和姿态信息，为后面的实验做好准备。

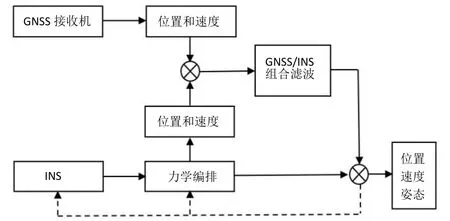
图1 GNSS/INS松组合的结构

2.1 INS原理

2.1.1 载体的经度、纬度和高程的计算

INS是一种以物理方法实现的导航定位技术。在该系统中设置有一个稳定的平台，通过此平台可以建立空间直角坐标系，用于模拟当地空间水平面。在坐标系中，坐标的三轴分别指向东、北和天顶三个方向。三轴上都安装有加速度计，用来测量载体在东、北和天顶三个方向上的加速度。对测得的加速度按式（1）进行积分计算后可得到三个方向上对应的速度[10-11]。

式（1）中：t1为当前时刻；t0为初始时刻；ve、vn、vu为记录载体在东、北和天顶三个方向上的速度；ae、an、au为加速度计测得的载体在三个方向上的加速度。

在动态定位中，根据载体的初始位置，对载体的速度进行积分可得到载体的连续位置。若以经度λ、纬度φ和h高程表示载体的位置，可根据式（2）来求解。

式（2）中：λ0、φ0、h0依次为载体的经度、纬度、高度的初始值；、、依次为载体的经度、纬度、高程随时间的变化率。

式（2）中、、可通过载体的速度来表示，如式（3）所示：

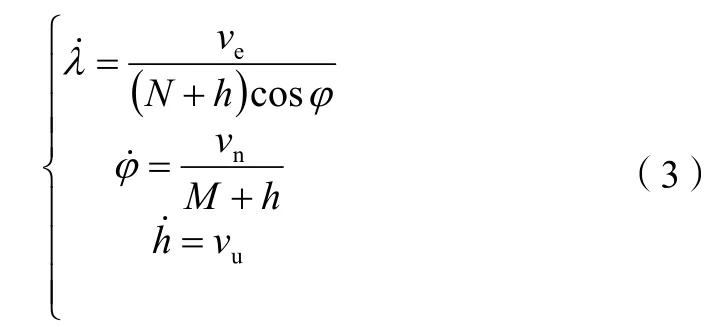
综合以上描述，载体的位置计算公式如式（4）所示：

式（4）中：N为卯酉曲率半径；M为椭球的子午圈曲率半径。

2.1.2 捷联式INS的结构

一个完整的INS结构应该包含有加速度计、陀螺仪、陀螺稳定平台、计算机、显示器、电源等，本文以捷联式惯性导航系统（Strap-down INS，SINS）为例来说明导航系统的结构。SINS的详细结构如图2所示。

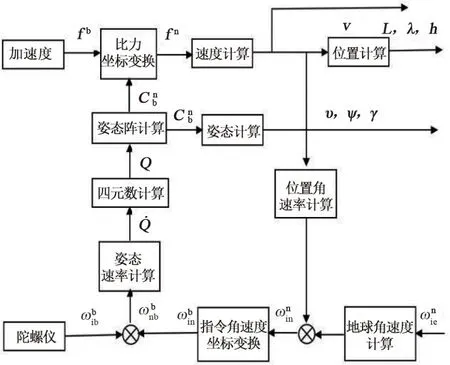
图2 捷联式INS的结构

在SINS中，加速度计和陀螺仪均直接固定在载体上。其中加速度计用来测量载体在运动过程中的加速度，根据2.1.1节中的描写计算出载体的位置。陀螺仪可测定载体运行的角速度，从而获取载体的姿态信息以及载体坐标系到计算坐标系（导航坐标系）之间的转换矩阵[10-11]。

2.2 卡尔曼滤波原理

GNSS/INS松组合导航系统中，在INS误差方程的基础上构建系统状态方程和量测方程需要用到卡尔曼滤波器；修正INS观测量从而进一步修改INS随时间累积的误差时也需要用卡尔曼滤波对INS的误差参数进行最小方差估计。这些操作得到的修正后的INS观测量能够提供更加精确的导航信息，从而更好地辅助GNSS系统，提高GNSS系统的稳定性和可行性[10-11]。

2.2.1 卡尔曼滤波方程

卡尔曼滤波方程是组系列方程，其中，卡尔曼先验状态估计方程为，卡尔曼先验协方差估计方程为，卡尔曼增益矩阵方程为，卡尔曼后验状态估计方程为，卡尔曼后验协方差估计方程为。

2.2.2 GNSS/INS松组合导航系统方程

松组合导航系统的状态参数向量可取为15维，参数分别为载体的位置、速度、姿态误差以及加速度计和陀螺仪在三轴上的偏差，也可以进一步增加状态参数向量的维数，加入尺度因子误差、重力误差以及天线偏差等误差参数，形成18维、27维等状态向量。GNSS/INS松组合导航系统的连续状态方程如下[10-11]：

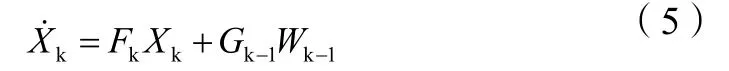
式（5）中：Fk为状态转移矩阵；Xk为系统的状态参数向量；Gk为动态噪声驱动矩阵；Wk为过程白噪声。

状态转移矩阵（以15维状态参数向量为例）见式（6）（7）（8）（9）：

组合导航系统参数状态向量为：

用泰勒级数展开系统的连续状态方程，可得到离散化的状态方程：

式（11）中：Xk为历元k的状态参数向量；Φk，k-1为离散化的状态转移矩阵；Xk-1为历元k-1的状态参数向量。

在组合中，将GNSS和INS各自输出的位置和速度分别作差，以差值作为系统的量测输入，从而构造出量测方程。观测方程如下：

式（12）中：Lk为观测向量；rGNSS、vGNSS和rINS、vINS分别为GNSS和INS输出的位置和速度信息。

系统的误差方程如下：

式（13）中：Vk为残差向量；Ak为观测矩阵；为参数状态向量。

GNSS/INS松组合方式的组合导航系统结构简单、易于实现、可行性比较高，是用户广泛采用的一种组合方式[10-11]。

3 GNSS/INS松组合导航程序设计

GNSS/INS松组合导航程序设计流程如图3所示：首先读取文件存放的GNSS位置、GNSS速度、INS加速度和陀螺仪等信息，初始化相关变量，通过相关的惯性导航传感器信息计算出位置和速度信息，然后将GNSS和INS的位置和速度利用卡尔曼滤波进行处理，最后得到运行结果。

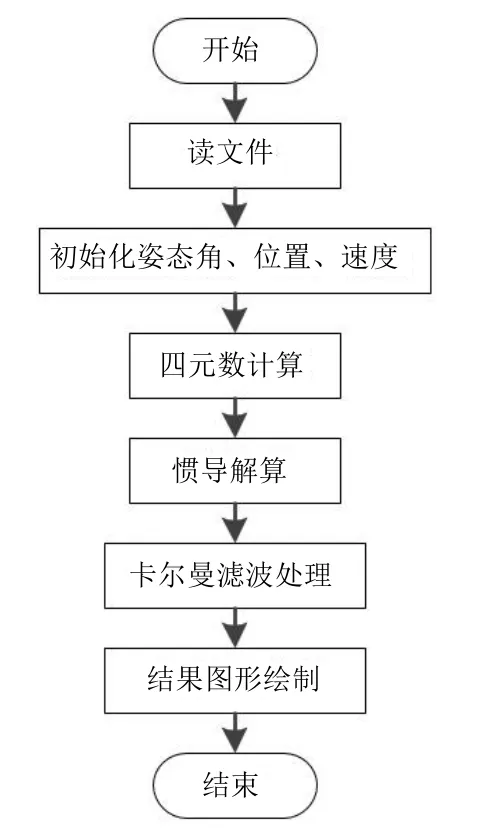
图3 程序流程图

4 GNSS/INS松组合导航仿真测试和分析

携带GNSS/INS松组合导航硬件平台在学校的操场走一圈，将采集到的数据保存成文件，利用MATLAB松组合系统程序读取真实数据进行处理，最后得到运行结果。松组合导航硬件电路板如图4所示。

图4 松组合导航硬件电路板

4.1 运行轨迹分析

运行轨迹如图5所示，东向GPS位置和组合导航位置误差如图6所示，北向GPS位置和组合导航位置误差如图7所示。

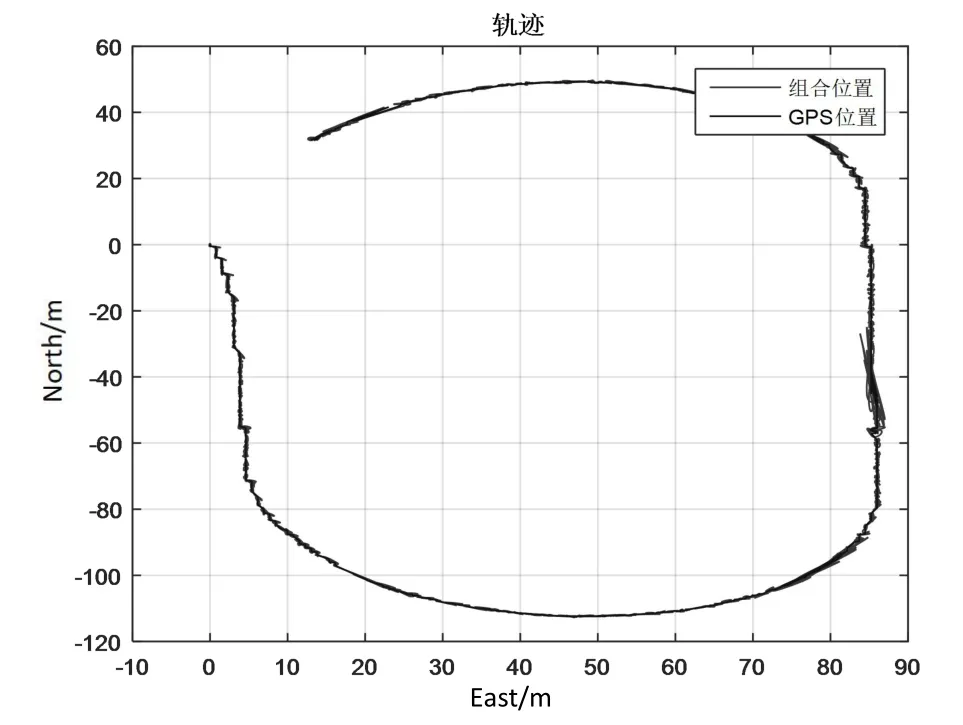
图5 运行轨迹

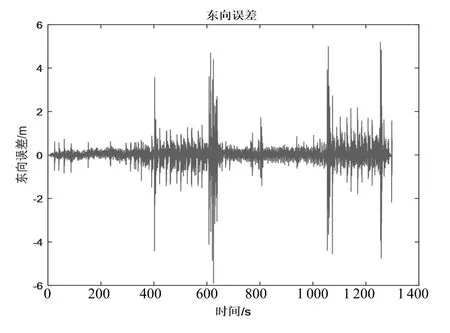
图6 东向GPS位置和组合导航位置误差

图7 北向GPS位置和组合导航位置误差

从图5～图7这三个图的位置误差来看，组合导航和单独GPS位置信息基本一致，说明组合导航有效。

4.2 东北天向速度分析

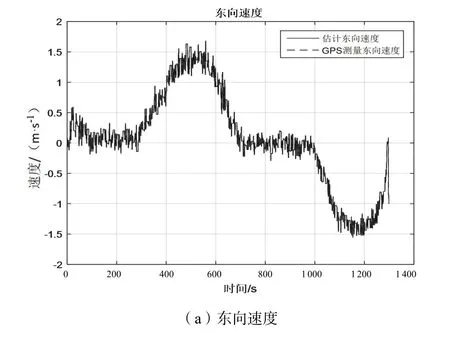
东向GPS和组合导航速度误差如图8所示，北向GPS和组合导航速度误差如图9所示，天向GPS和组合导航速度误差如图10所示。

图9 北向GPS和组合导航速度误差示意图

从图8～图10可以看出组合导航和单独GPS速度误差在10-3量级，基本可以忽略不计，说明组合导航信息有效。

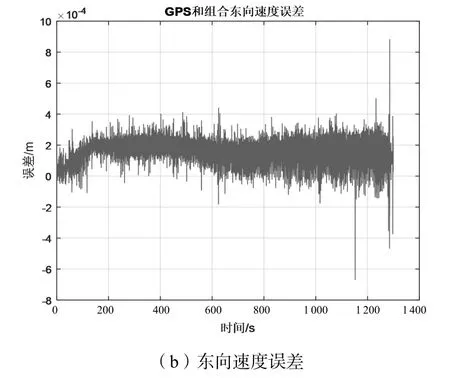
图8 东向GPS和组合导航速度误差示意图

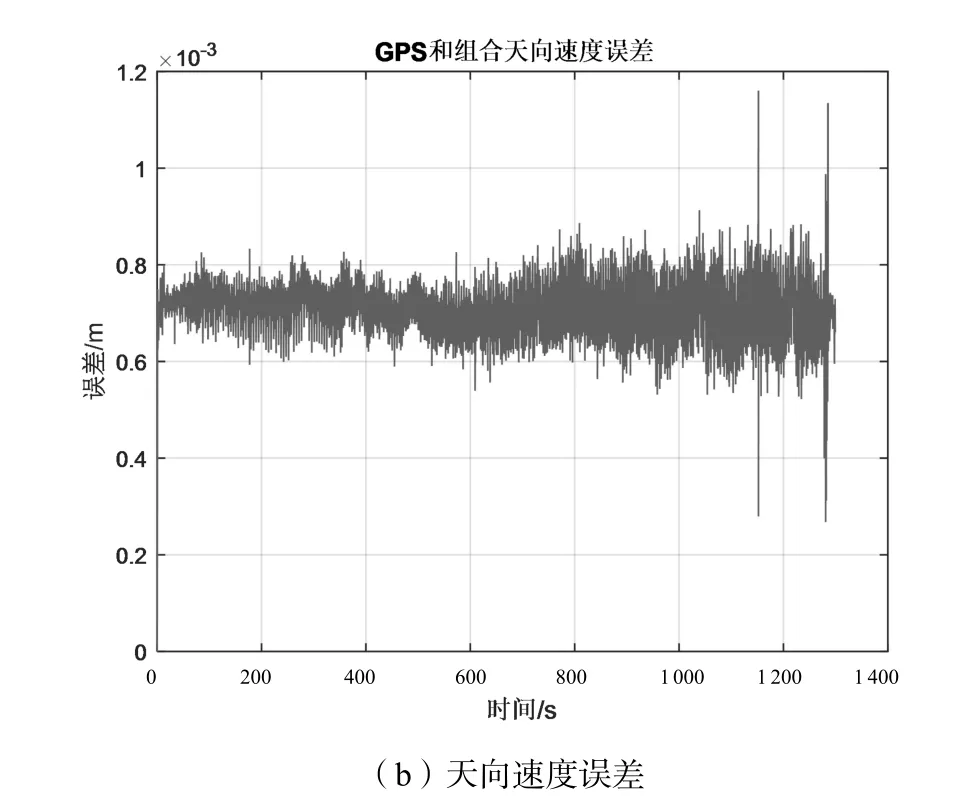
图10 天向GPS和组合导航速度误差示意图

4.3 误差收敛分析

东、北、天向速度误差和经纬度误差分析如图11所示。

从图11中可以看出东向和北向速度误差恒定在±0.5左右，误差收敛速度快，说明利用卡尔曼滤波能够很好地估计出误差，从而实时的校准INS信息。

图11 东、北、天向速度误差和经纬度误差分析图

综合以上可以得出：组合导航利用卡尔曼滤波器能很好地估计出误差并且实时的修正INS位置和速度，并且误差收敛速度快。

5 结语

以基于MATLAB松组合导航综合设计性实验为例，在此实验内容基础上，可深入结合更多的导航专业课程理论知识，拓展更多实验内容，丰富各种实验手段，提高综合设计性实验和创新性实验的自主性。学生依据相关的理论知识实现对实验内容的设计、仿真、调试和分析，从而提高学习兴趣并激发自主学习的积极性，培养学生的创新思维和解决复杂工程问题的能力。