基于参考压缩线的砂土压缩模型❋

2022-01-01张民生申志聪王振豪孔令明

中国海洋大学学报（自然科学版） 2021年4期

张民生，申志聪，王振豪，孔令明

(1. 北京航空航天大学交通科学与工程学院，北京 100191；2. 中国海洋大学环境科学与工程学院，山东青岛 266100；3. 北京建筑大学土木与交通工程学院，北京 100044)

砂土是一种结构简单但在高压下易颗粒破碎的散粒组合体，其基本力学特性主要有压硬性、摩擦性及剪胀性。由于颗粒间结构松散，极易扰动，制备土样孔隙比变化较大，导致砂土有许多压缩线，这是砂土区别于粘土的特征之一。砂土颗粒间接触面积极小，压缩过程中应力大于颗粒强度，从而产生颗粒破碎现象，这一力学特征也是砂土区别于粘土的显著标志。

在宽应力变化范围内，砂土的等向压缩具有以下特征：低压条件下，砂土压缩性较差，几乎不可压缩，体积变化主要以颗粒间的弹性变形为主，在V-lgp空间内压缩曲线变化缓慢；随着压力增加，砂土的压缩性显著增大，在一定应力区间压缩曲线斜率变化明显，该区间被认为是土颗粒破损或破碎的标志；在高应力区，不同密实度的试样压缩曲线趋向归并为同一条曲线[1-5]。

现有模型在描述砂土压缩时主要采用单对数方法、双对数方法、幂次方法及非线性函数方法。单对数方法假设孔隙比与压力的对数呈线性关系，这种方法对于粘土有很好的适用性，剑桥模型及修正剑桥模型[6]均采用该方法，虽然一些学者也采用此方法描述颗粒材料[7-8]，但该方法在描述低应力时存在一定的局限性。而且，单对数方法中孔隙比与固结(压缩)压力呈对数关系，当压力足够大时，孔隙比出现负值，这不符合试验规律。为克服单对数方法无法真实反映物理试验现象的问题，一些学者[2,9-10]提出了双对数法描述粘土固结特性，而Sheng等[2]利用该方法很好地描述了砂土低应力下的非线性压缩特性及临界状态线。幂次方法起初基于砂土弹性模量与压缩压力或垂直压力的幂次方呈正比[11]。由于砂土弹性模量的幂次表达方法在工程中受到广泛认可，且真实砂土临界状态线也符合幂次规律[5]，因此建立一个基于幂次变化规律的压缩曲线将对本构模型的建立提供极大方便。同时幂次函数用于描述低应力下砂土压缩特性[12]也具有一定的适用性，而且基于幂次函数描述砂土等向压缩特性已取得了一定的效果[1,3-4,13-16]。

本文在分析砂土的等向压缩特征基础上，依托临界状态线建立砂土等向压缩参考线，并通过塑性修正方法获取其它压缩线的斜率。建立的模型能够同时考虑塑性变形与弹性模量。利用已有砂土试验数据对模型进行验证。

1 砂土压缩模型

1.1 高压下砂土的极限孔隙比

常压下制备砂土存在最小孔隙比，随着压力增加最小孔隙比也会逐渐减小，极高压力下砂土颗粒发生破碎形成多个细小颗粒，导致颗粒间接触空间减小。当颗粒破碎到一定程度时不再发生破碎，接触空间也不再减小，从而形成了高压下的极限孔隙比。由于颗粒力学特性不同，不同的砂土破碎后形成的粒径大小及形状各不相同，因此高压下的极限孔隙比没有统一值。通过分析已有关于高压下不同砂土压缩试验[17]及剪切试验[18-19](试验压力大于50 MPa，见图1)，可以看出试验停止时，孔隙比主要在0.05～0.2区间内分布，即使在1 000 MPa下砂土的极限孔隙比仍然不为0，因此描述砂土压缩规律时应参考极限孔隙比影响。

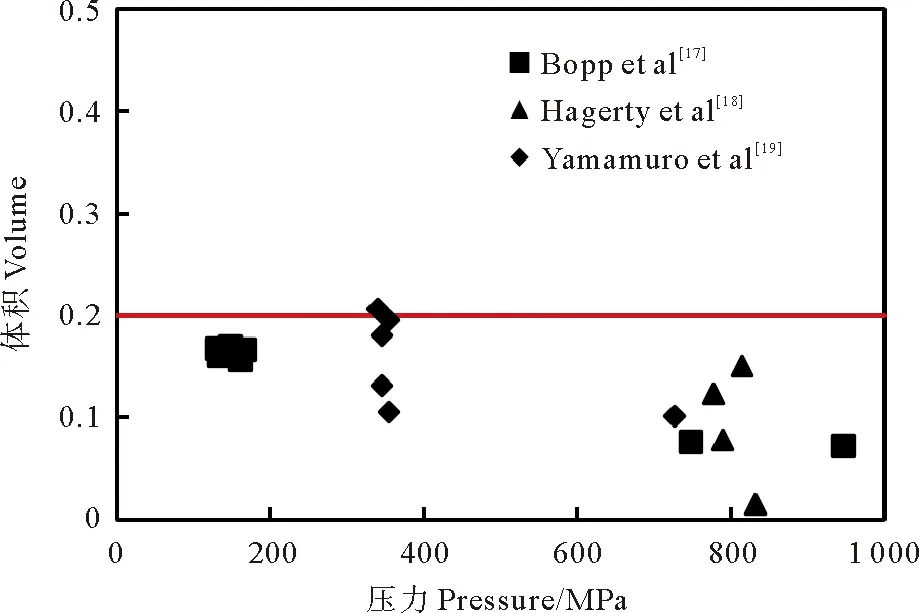
图1 极限孔隙比随压力分布Fig.1 Limited void ratio vary with pressure in V-lgp

1.2 砂土参考压缩线

饱和粘土的正常固结线是描述其在不同应力历史下固结特性的参考线。由于粘土颗粒的物理化学作用，正常固结线相对较为稳定且唯一，即土的应力状态与土的孔隙比之间存在着唯一性关系，而且这种关系可以通过粘土的等向固结试验获取。

而砂土颗粒构成则较为简单，容易扰动，导致低应力下制备的试样孔隙比变化较大，进而使得砂土的压缩线不唯一，也就是土的应力状态与砂土孔隙比之间唯一性关系不成立，从而增加了砂土压缩特性数学描述的困难。因此，寻找合适的等向压缩线作为参考线是有效描述砂土等向压缩特性关键，本文将该曲线称为参考压缩线。通过砂土的等向压缩试验可以发现不同孔隙比的砂土等向压缩线在高压下最终均会汇聚于同一条线[1]。参考压缩线作为其中的一条等向压缩线，最终也会与其它等向压缩线在高压下相汇聚。同时，Javanmardi等[20]与Sheng等[2]认为在双对数空间内同样存在一条参考状态线,该线与临界状态线(CSL)在压力为1 kPa时相交，并且在压力无限大时与临界状态线近似平行。姚仰平等[21]认为在压力为0时，粘土的固结状态与临界状态应该为同一状态，这意味着两者在压力为0时相交。基于前人的研究基础[2,20-21]，本文建议砂土参考压缩线特征：在压力为0时与临界状态线相交，在高压时与其它压缩线汇聚。

砂土等向压缩线及临界状态线(CSL)在V-lgp空间内的非线性变化特征促使学者寻找更好的数学函数来描述其压缩规律。为考虑极限孔隙比对等向压缩影响，本文采用V体积(V=1+e)对数与压力的幂次关系来描述砂土临界状态线和参考压缩线。以Toyoura[22]砂为例，采用以下公式拟合砂土CSL线为：

(1)

式中:p为压缩压力；Vc为p对应的背景状态体积；Vmin为高压下的极限体积；Vc0为临界状态线上p为0时的体积；λc为曲线斜率；ξ为材料常数,对于Toyoura砂取值2/3。从式(1)可以看出CSL线在ln(V-Vmin)-(p/pa)ξ空间内为直线段且斜率为λc。从图2中可以看出利用式1拟合的Toyoura砂临界状态线数据离散性较低，拟合效果较为理想。

根据假设，砂土的参考压缩线与临界状态线在0点相交，且数学表达方式与临界状态线相似，因此参考压缩线的表达式可表示为：

(2)

式中:Vr为参数压缩线上p对应的体积；Vr0为参考压缩线上压力为0时的体积；且Vr0=Vc0；λr为曲线斜率。如图2，取等体积下临界状态线和压缩线上A点和B点对应的压力pA与pB，分别代入式(1)与式(2)，并联立可得

(3)

图2 V-lgp空间内临界状态线及参考压缩线变化规律[22]Fig.2 The critical state line and reference compression curve in V-lgp space[22]

由式3可见，参考压缩线与CSL线在任意体积下所对应的压力比值恒定，这与粘土的性质是完全一致，说明用对数-幂次函数描述砂土压缩线具有合理性。图3为参考压缩线在V-lgp空间内分布规律。从图中可以看出：低压时曲线斜率接近于0，体积随压力变化极小；随着压力增加曲线斜率急剧变化后并在一定压力范围内保持相对稳定；在较大高压阶段曲线又逐渐变为缓平，此时已趋近临界体积。

图3 V-lgp平面内参考压缩线变化规律

根据参考压缩线与临界状态线之间的关系，在临界状态线已知条件下，可确定临界状态在压力为0时的体积Vc0。制备体积为Vc0的砂土进行等向压缩即可得到参考压缩线。此外，根据参考压缩线的定义，可根据不同压缩线在高压下汇聚于一条线这一基本试验规律而进行拟合得到。图4为Cambria砂[23]的压缩试验及三轴剪切试验结果。在假定Vmin为0.17，ξ为2/3前提下，利用公式1对临界状态线进行拟合得到Vc0，然后利用公式2调整参考压缩线斜率λr使与其在高压下与压缩曲线汇聚，从而得到λr的确定值。砂土在高压下会发生颗粒破碎，图中Cambria砂的临界状态和等向压缩试验均包含了砂土的颗粒破碎，本文建立的参考压缩线函数基于等向压缩试验和三轴剪切试验，因此曲线函数已将颗粒破碎及压缩作为一个整体来考虑。从对比结果可以看出参考压缩线在描述包含砂土颗粒破碎时仍然具有适用性。

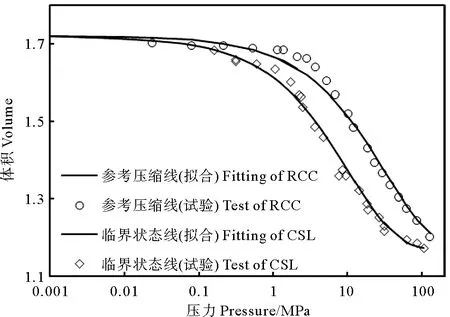
图4 Cambria砂的临界状态线及参考压缩线[23]

1.3 其它压缩线

对于其它压缩线的变化规律，本文采用增量形式表达，其思想是通过状态参量来修正参考压缩线。对式(2)进行微分可得：

(4)

假设砂土的弹性变形同样符合式(2)变化规律，则参考压缩线上当前体积对应的弹性增量可表示为：

(5)

式中κ为ln(V-Vmin)-(p/pa)ξ空间内的砂土弹性变形系数。式5表明砂土的弹性变形不仅与压力有关而且与孔隙比有关。Pestana等[1]及Chang等[24]采用过类似的方式来描述砂土的弹性变形。本文进一步考虑了极限体积的影响。砂土塑性变形可表示为：

(6)

由式6可以看出参考压缩线上塑性变形的增量同样与压力和体积有关。其它体积下砂土的塑性变形可利用塑性修正函数来修正，即：

(7)

式中：kn为恒大于0的材料参数；ψ为e-lgp空间内当前体积到参考压缩线的竖直距离(如图3所示)，即：

ψ=V-Vr。

(8)

将式7代入式6可得

(9)

最终得到不同体积下的压缩增量表达式为：

(10)

砂土体积应变增量则可表示为：

(11)

式中采用塑性修正方法求取其它体积下的压缩增量具有明显优势。式10中，exp(knψ)>0，λr-κ>0，则exp(knψ)(λr-κ)>0，这就保证了修正后的压缩曲线斜率恒大于κ，从而避免了数值计算过程中压缩变形呈现负增长的情形，保证数值计算稳定性。当前孔隙比位于参考压缩线上方时ψ>0，由于kn为恒大于0则exp(knψ)>1，(λr-κ)exp(knψ)+κ>λr，说明压缩线向参考压缩线趋近。当前孔隙比位于参考压缩线上方时ψ<0，exp(knψ)<1，(λr-κ)exp(knψ)+κ<λr，则等向压缩线相对于参考压缩线较为平缓。

1.4 弹性模量

(12)

则体积弹性模量K及剪切模量G则可表示为：

(13)

(14)

虽然假设砂土弹性变形在ln(V-Vmin)-(p/pa)ξ空间内只与压缩压力有关，但式13已体现出体积对体积弹性模量K的影响。从式13可以看出体积弹性模量K不仅随压缩压力升高而增加，也随着体积的减小而增加，很好地反映了砂土的压硬性及弹性模量的密实度相关性。

1.5 模型参数

建立的砂土压缩模型包括6个参数，Vmin、Vr0、λr、κ、ξ及kn。其中ξ为材料常数，当材料为粘土时取值为1[25]，对于各向同性压缩的颗粒材料，ξ趋近于2/3[1,24]，有些学者将ξ取值于0.7[5]或1/2[3,26]，本文取2/3。Vmin可取200 MPa压力对应的体积，对于Toyoura砂本文取值为1.2(见表1)。

表1 模型参数列表

κ为回弹曲线斜率，可在ln(V-Vmin)-(p/pa)ξ空间内利用砂土回弹曲线及最密压缩线拟合得到(如图5)。通过对Toyoura砂[22]压缩试验回弹曲线及最密压缩线的拟合得到曲线斜率分别为0.005、0.004 6及0.005 9(见图5)，本文取0.005 3。

Vr0与λr为参考压缩线所对应的初始体积和斜率，结合Toyoura砂临界状态线等向压缩试验，确定λr为0.013，Vr为1.944。

参数kn的数值可由姚仰平等[27]的硬化参量及Dafalias等[28]提出的状态参量确定。kn=4(nf-nd)，由文献nf为3.5，nd为-1.7，得到kn为20.8。

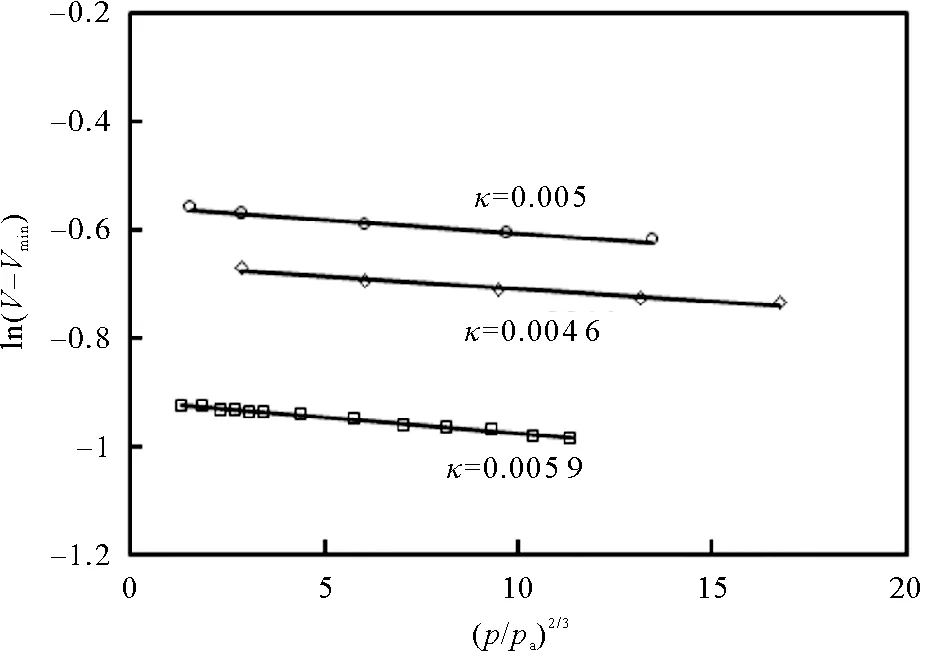
图5 κ标定结果

2 模型验证

图6为Toyoura砂土的压缩试验结果与模型预测对比，试验数据来源于Verdugo等[22]的饱和砂土的等向压缩试验，初始孔隙比分别为0.6、0.81、0.9及1.02对应的初始体积分别为1.6、1.81、1.9及2.02。从图6中可以看出，当前体积位于参考压缩线上时，压缩曲线斜率大于参考压缩线并向参考压缩线趋近。当前体积位于参考压缩下之下时，曲线相对于参考压缩线较为平缓，当前体积与参考压缩线的竖直距离越大则曲线平缓程度越高。模型预测的不同体积所对应的压缩线最终都汇聚于参考压缩线。从图中可以看出。预测体积变化趋势与试验结果也较为吻合，说明模型能够很好地描述不同体积和压力下砂土的压缩特性。

高中生独生子女多，受到家庭宠爱，以自我为中心，缺乏与外界的沟通交流，他们对思想道德的发展缺乏一定的认识。他们自尊心强，缺乏自我思想道德管理的能力，敷衍对待思想教育管理。

图6 Toyoura砂压缩试验结果与预测对比[22]

图7为Miura 等[29]开展的Toyoura砂的三轴压缩试验。试验砂土比重为2.64，最大颗粒直径为0.25 mm，不均匀系数为1.5，最大孔隙比为0.92，最小孔隙比为0.58，试验试样初始孔隙比与体积分别为0.83和1.83。整个试验进行了3次加载和2次卸载过程：首先由300 kPa的起始压力加载至10 MPa(体积约为1.728)，然后卸载至200 kPa(体积约为1.77)；继续加载至17 MPa(体积约为1.666)，再次卸载至488 kPa(体积约为1.71)；最后再次加载至20 MPa。本文预测了3次加载过程，从图中可以看出由于初始体积位于参考压缩线之下，加载时压缩线斜率相对较为平缓，当前体积距参考压缩线越大，则曲线越平缓。图7显示模型预测结果与砂土压缩试验结果较为一致，同样很好地反映了砂土的压缩特性。

图7 Toyoura砂加卸载试验结果与模型预测对比[29]

现有弹性模量试验手段除压缩试验外，还有弯曲元试验、共振柱试验及现场剪切波速试验，这些方法均属于小变形范畴。而本文所采用的砂土模量是基于中等变形范畴的压缩试验规律得到的。由于砂土的弹性模量与其应变水平相关，应变越小弹性模量越大，并且弹性模量随着应变水平的增加呈现规律变化。为验证体积对弹性模量变化趋势影响，分别采用应变因子FRC(γ)=3和FBE(γ)=3.85对共振柱试验(RC)与弯曲元(BE)试验数据进行归一化处理。图8为预测Toyoura砂的剪切模量与弯曲元及共振柱试验数据[30]对比。试验数据采用围压为100、200和500 kPa时Toyoura砂的共振柱和弯曲元试验结果，通过试验数据可以看出在相同围压下剪切模量随着体积的减小呈非线性增加，而预测的剪切模量变化趋势与实测模量变化趋势较为一致，说明本文提出的压缩模型同样能够较为可靠地预测砂土弹性变形趋势。

图8 Toyoura砂土剪切模量与体积变化关系[30]

通过分析模型特点以及模型预测与试验对比结果，基于体积的对数与压力的幂次关系构建的砂土压缩模型，不仅表现了砂土在低应力段的小变形特征及高压下的近似线性关系，而且能够表现出极限体积附近的低压缩性特征，能够很好地描述砂土全压力下的压缩特性。与现有单对数函数描述的砂土压缩曲线相比，模型在低压下的变形特征及极限体积附近的变形特征描均具有明显优点。同时，在该关系函数框架下建立的弹性模量表达式能够很好地描述体积弹性模量随体积变化趋势。

相对来说，利用CSL线来确定参考压缩线进而描述砂土等向压缩特性的工作稍显复杂，且砂土CSL线的建立需要一定数量的高质量三轴剪切试验数据。但从参考压缩线的建立过程可以看出，本文已经建立CSL线与参考压缩线的相关关系，这是建立砂土二维本构模型最为重要的工作之一，因此建立的CSL线与参考压缩线的相关关系不仅适用于砂土等向压缩描述，而且能够为砂土二维模型建立提供理论依据。从长远角度，这种复杂的工作还是值得去探索的。