自适应非局部均值滤波与小波相结合的脑部CT去噪研究

2021-12-31张爱桃陈小茜肖雨郭东敏周旭李连捷

中国医疗设备 2021年12期

张爱桃，陈小茜，肖雨，郭东敏，周旭，李连捷

河北医科大学医学影像学院，河北石家庄 050017

引言

目前，随着医疗科技日趋发达，医学影像技术已经广泛应用于医学诊断和临床治疗，其中CT影像检查技术[1-2]具有图像分辨率高、操作便利、无创等诸多优点，适用于多种疾病的临床诊断和病情评估。脑部疾病由于不便取样本探查，脑部CT[3]成像成为脑部疾病临床诊断最重要的辅助工具之一。但是由于CT成像的机制，图像在获取和传输的过程中不可避免地要受到噪声的污染，噪声导致图像质量下降、组织边界模糊、细微结构难以辨认，不仅影响医生对病情的诊断和治疗，而且严重阻碍图像的后续处理。因此，抑制CT图像噪声[4-5]成为医学图像处理领域的基础和热点之一[6]。对于依赖信号强度的乘性噪声主要采用基于投影域的方法，近似于白噪声的加性噪声主要采用基于图像域的方法。在日常生活中，最常见的CT图像噪声是高斯白噪声[7]。目前，针对高斯白噪声的处理方法，主要有空间域中的以平滑为基本思想的均值滤波、高斯滤波[8]、局部滤波[9]等，此外还有频率域中的维纳滤波[10]和小波阈值收缩[11-14]等。局部强度统计特征是衡量区域内像素间的平均相似性，但这一特征难以准确辨别边缘与其邻近点之间的差异，导致了滤波结果中边缘信息的模糊。小波阈值收缩算法虽能够很好地估计信号的噪声，但是阈值和阈值函数的选择上存在不确定性，会造成信号的失真。2005年Buades等[15]提出了去除图像加性噪声的非局部均值滤波算法（Non-Local Means，NLM），该算法是利用图像非局部结构的相似性来去除噪声，恢复图像的主要几何结构。脑CT 图像具有很强的对称性和非局部区域相似的特性，因此本文根据脑CT图像的特性提出一种新的结合小波变换的非局部均值脑CT图像滤波算法的改进方案。

1 结合小波变换的自适应NLM算法

1.1 非局部均值滤波

非局部均值滤波[15]是考虑到图像的非局部统计自相似性质，利用图像包含的大量重复结构进行去噪。通过计算非局部像素之间的相似度确定权值，然后加权平均来恢复图像。NLM的主要特点：将相似像素定义为具有相同邻域模式的像素，对像素周围固定大小的窗口内的信息进行比较，而不只是比较图像单个像素的信息，因此得到的相似性更加可靠。其基本原理如下：对于一幅含加性噪声图像，见公式(1)。

其中X(i)为未受噪声污染的原始图像；N(i)为均值为0，方差为σ2的高斯白噪声，I为图像域对于任意像素点i，它的非局部均值评估值NL[Y](i)可以通过在图像中所有的像素加权平均得到，见公式(2)。

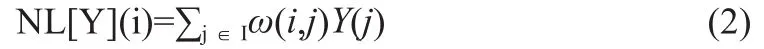
其中，权值ω(i,j)由像素i,j的相似度决定，见公式(3)。

其中，Ni,Nj是分别以像素i,j为中心点的图像块，α＞0是高斯核标准偏差，为高斯加权的欧几里得距离，高斯加权意味着距离中心像素越远，权值就越小。h为滤波参数，控制着指数函数的衰减，也就是控制着欧氏距离对权重的均质化程度。Z(i)为权值的归一化常量，见公式(4)。

从定义中可以看出ω(i,j)的值在区间[0,1]之间，且∑ω(i,j)=1。当两个像素邻域之间的相似度越高，加权欧式距离越小，权值越大。由于这种相似度考虑了像素邻域的信息而不是用单个像素的值进行比较，因此保持了去噪算法的稳定性，同时高斯加权又增加了中心像素点的权重，使得重构信号较好地保留了细节特征。

滤波参数h控制着权重的均质化程度,当h较大时，ω(i,j)均质化程度高，平滑效果比较好。反之h较小时，均质化程度低，图像细节保留程度较高。因此，当图像噪声水平较高时，则需要相对较大的h平滑噪声[16]；反之当图像的噪声水平较低时，就需要相对小的h去保留图像细节。本文中滤波参数的取值由噪声方差确定，见公式(5)。

其中，k为调节系数，σ为噪声标准差。

1.2 仿真数据处理

为了定量分析NLM算法的滤波参数的设置及去噪效果，本文首先进行了仿真实验。在仿真实验中，不同程度的高斯白噪声以式(1)的形式添加到Shepp-Logan头部模型仿真CT图像（图1）中，然后分别采用原始非局部均值滤波、本文算法进行去噪处理（邻域窗口Ni采用77，搜索窗口采用1313），比较去噪效果。为了定量地评估算法的去噪性能，采用去噪前后图像的峰值信噪比（Peak Signal to Noise Ratio，PSNR）做为度量[17]。

图1 Shepp-Logan头模型仿真CT图像

1.3 真实脑CT图像处理

为了验证仿真实验研究的可行性，本文采集了三幅真实人脑的CT图像，分别采用原始非局部均值滤波（h2=100σ2）[18]和本文提出的滤波算法进行去噪处理，比较去噪效果。仿真实验所用图像噪声方差是已知的，但是在临床实践中脑CT图像噪声方差是未知的，所以还需估计脑CT图像的噪声方差，本文采用由Donoho和Johnstone提出的小波域噪声方差估计[19]，并对其进行了验证，证明了其可靠性。

本实验应用MATLAB 2014a软件完成算法，应用SPSS 22.0软件对数据结果进行统计学分析。采用配对t检验，对滤波前后的图像信噪比数据进行统计学分析，以P＜0.05为差异有统计学意义。

2 结果分析

2.1 仿真实验的处理结果

本文采用15组不同噪声水平的高斯白噪声样本仿真图像（W1～W15）验证算法的有效性。图2是三组不同峰值信噪比图像[W6 (PSNR=15.4658)，W10 (PSNR=7.6972)，W15 (PSNR=5.9949)]滤波前后的结果对比，图2a、2d、2g分别为W6、W10、W15去噪之前的图像，将这三幅图像分别运用原始非局部均值滤波后的效果如图2b、2e、2h，可以看到滤波后图像边缘及细节出现模糊，且随着信噪比的降低，滤波后图像细节损失更加严重。通过本文提出的滤波算法处理后图像（图2c、2f、2i）边缘清晰，随着信噪比的降低细节模糊程度较轻，该算法对不同信噪比的图像具有自适应性，且PSNR明显高于原始非局部均值滤波后的（表1），15组含有不同强度噪声的图像通过本文算法滤波后的PSNR远远高于未处理图像及原始非局部均值滤波后图像的PSNR（图3）。对未处理图像与经过本文算法去噪后的图像的PSNR（表2）采用配对t检验进行比较分析，差异有统计学意义（P＜0.001）。

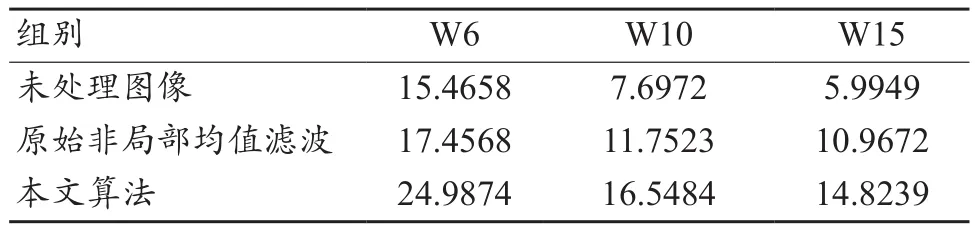
表1 不同噪声水平的图像去噪前后PSNR比较

表2 仿真图像去噪前后PSNR

图2 不同噪声水平的图像去噪效果图

图3 仿真图像去噪前后PSNR统计

通过仿真实验发现，本文滤波算法中的调节系数k的最优值（即k取该值时处理后的PSNR最高）与去噪前图像的PSNR具有线性关系，见图4。

图4 最优k值与图像PSNR的关系

根据图像拟合出的函数关系式如公式(6)所示。

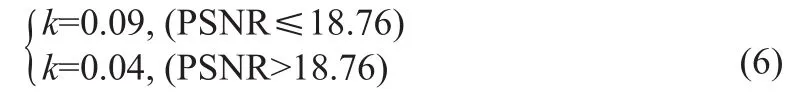
由此，调节系数k的值可以根据所需处理图像的PSNR自适应选取。

2.2 真实数据处理结果

本文选用了三幅PSNR水平不同的真实人类脑CT图像来验证算法的有效性，并且将该算法与原始非局部均值算法滤波方法进行了对比实验。

在估计脑CT图像的噪声方差时，由Donoho和Johnstone提出的小波域噪声方差估计[19]，见公式(7)。

其中，MAD是HH子带（HH子带表示水平高频和垂直高频信息）小波系数幅度的中值，σ为图像噪声标准差。由于在最小细化对角子带，即HH子带中信号能量很小，所以认为含噪图像的HH子带主要由噪声组成，可以在该子带进行噪声方差估计[20]。

本文先采用Shepp-Logan头模型仿真CT图像（图1）对该噪声估计方法进行了验证。给图1分别加入不同程度的噪声，利用式(6)对估计的含噪图像的噪声标准差和真实噪声标准差进行对比，结果如图5所示，两者非常接近，差异无统计学意义（P=0.321＞0.05），所以本文采取了这种方法。

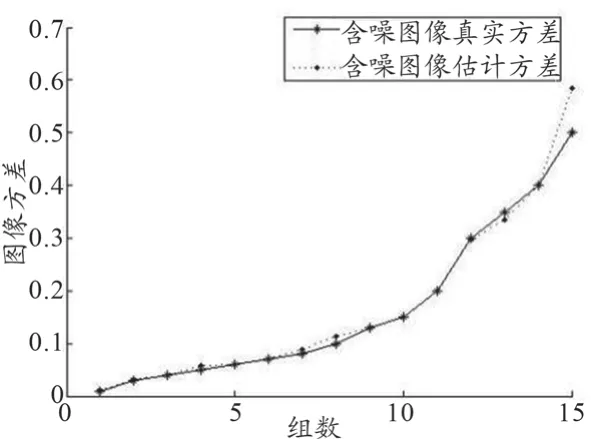
图5 含噪图像方差与小波域估计方差对比

在对三幅真实脑CT图像进行处理过程中发现，仿真实验中的调节系数k的取值规律，同样适合该真实数据处理。这三幅含噪图像的PSNR及k的取值如表3所示，去噪结果如图6所示，可以看出，原始的非局部均值滤波不仅需要手动调节参数h，还容易导致图像过于平滑，PSNR降低（表4），而本文提出的滤波算法，可以根据输入图像的PSNR自适应选取滤波参数，在抑制噪声的同时很好地保留了图像的细节及边缘，提高PSNR（表4）。所以无论从视觉效果还是图像PSNR的提高上，本文提出的算法都具有更好的效果。

图6 真实数据的处理结果

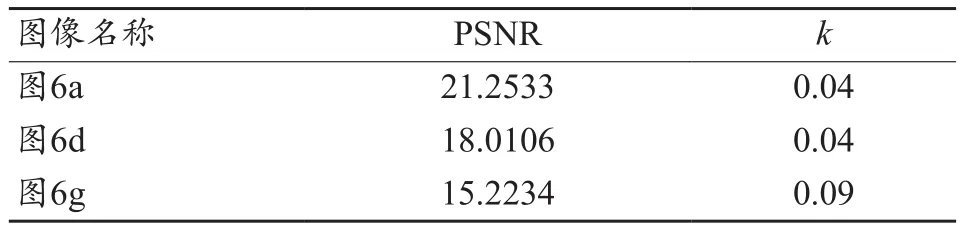
表3 三幅含噪图像的PSNR及k的取值

表4 真实脑部CT图像去噪前后PSNR的比较

3 讨论

由于脑部CT图像具有很强的对称性和非局部区域相似的特性，本文提出了结合小波的自适应非局部均值滤波算法对其存在的高斯白噪声进行去噪处理。仿真实验表明该算法能够有效地抑制白噪声，并在真实的脑部图像处理中也验证了其可靠性。

该算法中滤波参数h和滤波窗口的设置非常关键。滤波参数h控制噪声的抑制程度，当h较大时，幂函数的衰减较慢，平滑效果比较好；反之h较小时，图像细节保留程度较高，因此，h的取值当由图像噪声水平决定。原始的非局部均值滤波需要手动调节参数h，从而容易导致图像过于平滑，本文提出滤波参数的取值由噪声方差确定，即h2=k×σ2，通过仿真实验我们得出调节系数k的最优值与图像的PSNR具有线性关系，并且在真实的脑部CT图像中也得到了验证。处理真实脑部CT图像时，由于噪声方差未知，本文采用小波域噪声方差估计法对其进行计算，并且验证了其有效性。因此结合小波的自适应非局部均值滤波算法能够根据输入图像的PSNR，自适应地设定滤波参数，在抑制噪声的同时很好地保留了图像的细节及边缘。

由于脑部图像非局部的相似性非常高，搜索窗口应该尽量大，因此理想情况下应该定义为整幅图像，但是考虑到计算效率，本文中图像的搜索窗口统一定为13×13。邻域窗口的大小应该取决于图像的噪声水平，信噪比高时应减小窗口，反之应增大窗口，但是窗口过大又会造成图像细节的损失。本文中邻域窗口根据经验设定为7×7，无法根据噪声水平自适应地改变，因此邻域窗口的大小与图像噪声水平的关系有待于进行进一步深入实验研究。