深度卷积神经网络权重参数更新方法研究
2021-12-31杨曼黄远民石远豪
杨曼,黄远民,石远豪
(1.佛山职业技术学院,广东 佛山 528137;2.佛山赛宝信息产业技术研究院有限公司,广东 佛山 528000)
1 权重参数更新方法
1.1 随机梯度下降法(SGD)
一般而言,损失函数很复杂,参数空间庞大,而通过巧妙的使用梯度来寻找函数最小值的方法就是梯度法,梯度表示的是各点处的函数值减小最多的方向。在神经网络的学习中,寻找最小值的梯度法称为梯度下降法,由于神经网络中选取的训练数据多为随机批量数据,因此称为随机梯度下降法。用数学公式来表示方法如下式所示:

1.2 Momentum
在使用SGD训练参数时,SGD每次都会在当前位置上沿着负梯度方向更新,并不考虑之前的方向梯度大小,有时候会下降的非常慢,并且可能会陷入到局部最小值中,动量的引入就是为了加快学习过程,引入一个新的变量去积累之前的梯度(通过指数衰减平均得到),实现加速学习过程的目的。用数学公式来表示方法如下式所示:

这里变量v表示物体在梯度方向上的受力,遵循在力的作用下,物体的速度增加这一法则,v初始为None,若当前的梯度方向与累积的历史梯度方向一致,则当前的梯度会被加强,从而这一步下降的幅度更大。若当前的梯度方向与累积的梯度方向不一致,则会减弱当前下降的梯度幅度。a初始值设定为0.5、0.9或者0.99。
1.3 AdaGrad
AdaGrad算法的思想是每一次更新参数,不同的参数使用不同的学习率。将每一个参数的每一次迭代的梯度取平方累加后再开方,用全局学习率除以这个数,作为学习率的动态更新。用数学公式来表示AdaGrad方法如下式所示:这里变量h保存了所有梯度值的平方和,在更新参数时,通过乘以来调整学习的尺度,参数元素中被大幅更新的元素的学习率将变小。从算法AdaGrad中可以看出,随着算法不断迭代,h会越来越大,整体的学习率会越来越小。

1.4 Adam
Adam方法计算了梯度的指数移动均值,融合了RMSProp和Momentum的方法,Adam会设置3个超参数,一个是学习率,标准值设定为0.001,另外两个超参数beta1和beta2控制了这些移动均值的衰减率,移动均值的初始值beta1、beta2值接近于1,在深度学习库中,标准的设定值是beta1=0.9、beta2=0.999。
2 算法对比
MNIST数据集60000个训练数据样本,构建5层神经网络,输入层数据大小为784,隐藏层神经元个数分别为600、400、200,输出层神经元个数为10,激活函数用relu。
其迭代后损失函数结果如下表1所示(保留4位有效数字)。

表1 损失函数值
根据以上数据可得到损失AdaGrad函数最小为.0105,Adam次之且相差不大,其余两种方法学习效率较低。
其迭代后损失函数结果如下表2所示(保留4位有效数字)。

表2 损失函数值
根据以上数据可得到Adam损失函数最小为。0.0019,在神经网络层数不变,神经元个数不变的情况下,增加训练样本的迭代次数,AdaGrad的损失函数更新速度变慢,Adam方法损失函数更新速度更快、效果更好,此时损失函数值更小。
3 实例应用
以MNIST数据集为例,分别采用SGD、Momentum、AdaGrad、Adam方法对目标函数进行优化,构建以下深度CNN网络结构图,见图1。完成对该数据集中手写数字的分类识别。
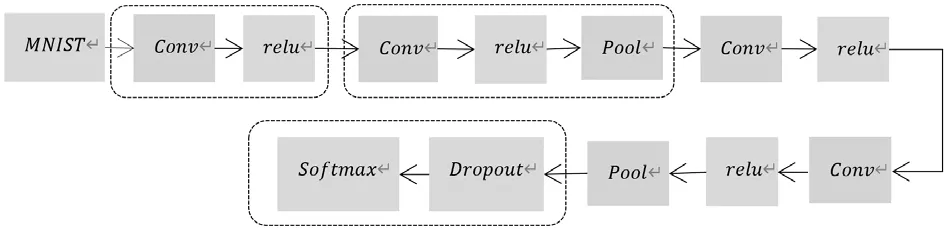
图1 深度网络结构图
其中Conv为卷积层,主要进行卷积运算,相当于图像处理中的滤波器运算。Pool为池化层,主要是缩小高、长方向上的空间运算。Dropout是一种在学习的过程中随机删除神经元的抑制过拟合问题的方法,训练时随机选出隐藏层的神经元,然后将其删除,被删除的神经元不再进行信号的传递。softmax函数为输出层函数,softmax函数的输出是0.0到1.0之间的实数。采用上述深度卷积神经网络进行测试,当epochs=12,得到准确率如下表3所示。

表3 测试结果
结果显示,采用Adam进行目标函数优化,分类识别准确率为0.9951。设定当epochs=20,得到准确率如下表4所示。

表4 测试结果
结果显示,增大epochs后,采用Adam 进行目标函数优化,分类识别准确率仍为最高0.9955。增加了0.04%,但计算速度会减慢。
4 结语
采用SGD、Momentum、AdaGrad、Adam 4种权重参数更新方法,SGD下降过程更为曲折,因噪声使梯度更新的准确率下降,同时SGD会在某一维度上梯度更新较大产生振荡,可能会越过最优解并逐渐发散。加入动量Momentum梯度移动更为平滑,但效率仍偏低。AdaGrad可根据自变量在各个维度的梯度值大小来调整各个维度上的学习率,避免统一的学习率难以适应所有维度的问题。Adam融合了Momentum、AdaGrad的方法,Adam的更新过程类似Momentum,但相比之下,Adam晃动的程度有所减轻。以MNIST数据集为样本集,构建深度卷积神经网络结构,分别采用SGD、Momentum、AdaGrad、Adam方法对目标函数进行优化,完成对该数据集中手写数字的分类识别,结果对比显示采用方法,识别准确率为99.55%。
