工程机械数字线控转向系统研究

朱耿寅,朱 涛,谢 广,姜友山，吴岳岭

（山推工程机械股份有限公司，山东 济宁 272073）

目前，传统的轮式工程机械，例如压路机、平地机、转载机等行走转向都使用转向器，转向泵的高压油经过转向器进入转向油缸来控制转向油缸活塞的伸缩，实现装载机铰接点转动，一般转向器控制精度低，在实际操作中一部分高压油溢流回油箱，造成了发动机能量的浪费。

随着转向系统的更新换代又推出了一系列新的转向技术，机械反馈随动转向系统、全液压转向系统、同轴流量放大转向系统、负荷传感转向系统等，这种技术虽然在一定条件下降低了能耗，但是没有从本质上解决问题。

1 数字转向液压系统分析

随着现代电子技术、计算机技术、通讯技术、人工智能技术、和传感器技术等高新技术相结合，传统轮式行走工程机械转向液压系统正向线控数字化方向发展。

图1 是一种数字线控转向系统，采用传统方向盘，其下装有角度传感器，可以精确地检测方向盘转角，方向盘转动时，转向力及转角经过减速机构传递后到达力反馈电机，力反馈电机的控制信号经过A/D 转换器进入控制器，控制器输出数字信号并将数字信号传递给数字换向阀上的步进电机，步进电机带动阀芯运动，实现阀口的开闭及大小控制；同时转向泵打出的高压油经过阀口进入转向油缸，为保证整个液压系统的安全，设计了溢流阀，为保证整个液压系统的转向压力值且使数字方向流量阀进出口压差为常数，保证转向速度稳定，同时还可以减少管路压力损失设计了定压差阀压力补偿装置。此时，转向缸的伸缩完成转向，转向油缸活塞上的位移传感器及油缸进出油口的压力传感器，实时的检测活塞的位移及系统压力并经过A/D 转换器后反馈给控制器，这时方向盘的输入信号与转向油缸的反馈信号进行比较，形成了一个闭环反馈系统，实现了转向的精确控制。

图1 数字线控转向系统原理图

2 数字线控转向控制系统分析

传统的PID 控制由于原理简单，适应性强而被广泛用于工程机械控制系统上，但是传统的PID 控制存在缺陷，控制精度低，抗干扰能力差，整定参数后系统参数是固定不变的；而在实际的工程应用中，工程设备都视为高阶控制系统，系统的参数是随着时间和周围环境时刻变化的，被控参数存在着随机性和偶然性。而模糊自适应PID 控制在传统PID 控制上，以误差e及误差变化率ec作为输入，再利用设定好的模糊规则进行分析及推理计算，比例、积分、微分三个参数会根据外界环境变化自动调整，来满足不同状态下的误差e及误差变化率ec对PID 参数自整定的要求，以保证控制系统的稳定性，同时可以是系统具有良好的动、静特性，其控制原理如图2所示。

图2 模糊自适应整定PID控制器原理图

自适应模糊控制在建模时，可利用模糊集合理论同时建立比例参数Kp、微分参数Ti、积分参数Td与误差绝对值|e|和误差变化量绝对值|ec|的关系：

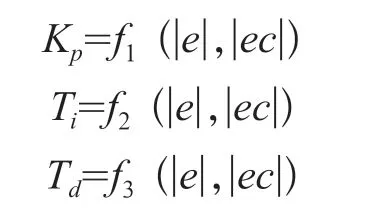
根据经验，在不同的情况下误差绝对值|e|和误差变化量绝对值|ec|对参数Kp、Ti、Td的自整定要求可以归纳为以下三点。

1）当误差绝对值|e|较大时，为了保证控制系统有快速跟踪性，避免系统出现较大的超调量应，此时Kp的取值较大、Td取值较小，Ti=0。

2）当误差绝对值|e|中等大小时，保证系统有较小的超调量，Kp取值较小，Td的取值较大，Ti适中。

3）当误差绝对值|e|较小时，为保证系统良好的稳态性能，避免出现振荡，Kp与Ti取值较大，Td值根据系统实际情况取值。

根据实际经验进行推力和判断，建立整定的3 个参数Kp、Ti、Td的模糊规则表并根据隶属度和模糊控制模型，列出模糊矩阵表，将选定的修正参数代入下列公式计算

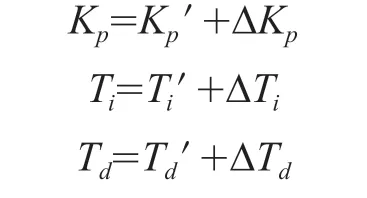
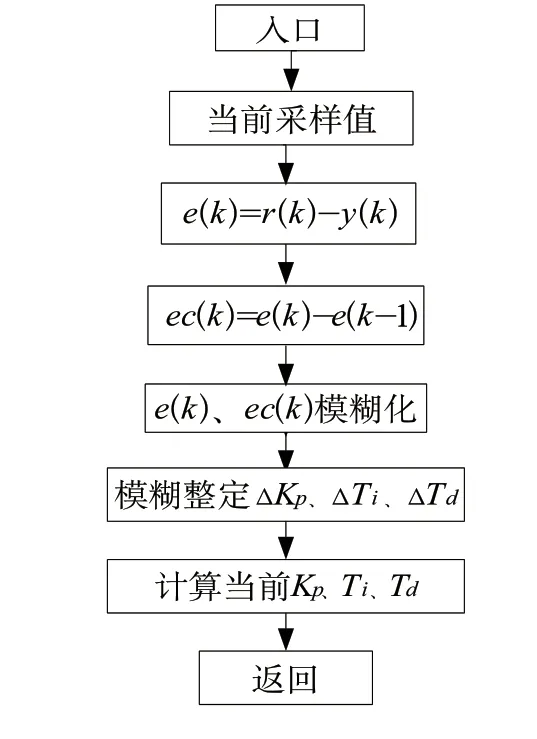
图3 模糊PID控制参数自校定流程

3 数字转向液压系统数学模型

在建立数字转向液压系统数学模型时，数字液压阀是重点，根据经验对一些参数进行了简化，这对整体数学模型没有影响。

3.1 步进电机的数学模型

步进电机输入脉冲信号，输出转角位移信号，力矩方程

式中，Tb为电机力矩，Nm；Ti为电机最大静转矩，Nm；Z为转子齿数；θm为旋转磁场角，°；θ为转子的转角，°。

步进电机转子动力学方程

其中，J为转动惯量，kgm2；B为阻尼系数，Ns/m。

步进电机凸轮机械转换器将转角位移转换成直线位移

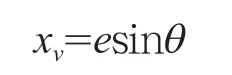
其中，xv为直线位移，m；e为凸轮偏心轮转角，θ为偏心距。

3.2 压力补偿阀数学模型

压力补偿阀阀芯力平衡方程

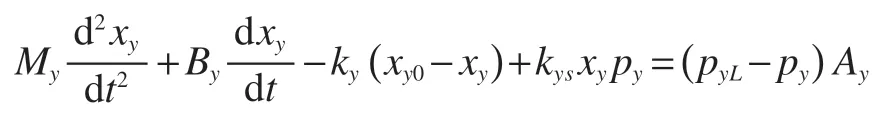
其中，My为阀芯质量，kg；By为阻尼系数，Ns/m；ky为弹簧刚度，N/m；xy0为弹簧初始位移，m；xy为阀芯运动位移，m；kys为液动力刚度；py为进油口压力，Pa；pyL为控制口压力，Pa；Ay为两腔横截面积，m2。

流入压力补偿阀的流量等于流出的流量，则流量连续性方程

其中，qy为流入压力补偿阀的流量，m3/s；qy1为左腔流出的流量，m3/s；qy2为从阻尼孔流出的流量，m3/s；qyt为从出口流出的油液流量，m3/s；Vy0为受控腔面积，m2；βe为体积弹性模量，Pa。

出口流量方程

其中，Cyd为流量系数；kyq为流量增益；kyc为压力-流量系数。

3.3 减压阀数学模型

减压阀的阀芯力平衡方程

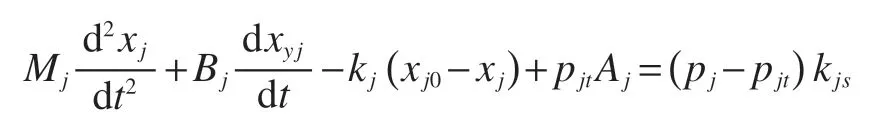
其中，Mj为减压阀阀芯质量，kg；xj为阀芯位移，m；Bj为阀芯运动阻尼，Ns/m；kj为弹簧刚度，N/m；xj0为弹簧预压缩量，m；pj、pjt为进、出油口压力，Pa；Aj为出油腔受力面积，m2；kjs为液动力系数。

减压阀的流量连续性方程

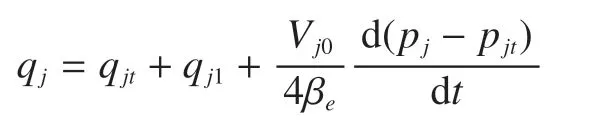
其中，qj为流入的流量，m3/s；qjt为流出的流量，m3/s；qj1为阻尼孔流量，m3/s；Vj0为控制腔体积，m3。

减压阀出口流量方程

其中，Cjd为流量系数；Dj为出油口直径，m；kjq为压力流量增益。

3.4 数字阀主阀的数学建模

数字方向流量阀主阀芯力平衡方程

其中，M为主阀芯质量，kg；x为主阀芯位移，m；B为主阀芯运动阻尼，Ns/m；k为主阀弹簧刚度，N/m；x0为弹簧预压缩量，m；ks为液动力系数；p为进口压力，Pa；pL为主阀A（B）口的压力，Pa；p1、p2为主阀左腔和右腔压力，Pa；A1、A2为主阀左腔和右腔横截面积，m2。

数字方向流量阀主阀流量连续性方程

其中，q为流入流量，m3/s；A为主阀腔面积，m2；V0为进油腔体积，m3。

流入数字方向流量阀的流量

其中，kq为主阀的流量系数；kc为主阀的流量-压力系数。

对上述公式进行拉普拉斯变换后，可以推导出传递函数，可以对传递函数进行仿真分析，验证系统动静态特性。

4 结语

数字线控转向系统提高了轮式工程机械的转向精度，适用于精准作业环境，同时，数字线控转向系统提高了泵的使用效率，合理的分配发动机功率，降低了能耗，提高了轮式工程机械操纵技能；数字线控转向系统暂用空间少，管路布置比较简单，使整车结构更加紧凑，噪音小，优化操作环境，数字式线控转向系统可以形成模块化，更容易实现智能化操作、无人驾驶，未来数字线控转向将是转向技术主要发展趋势之一。