考虑设备相关性的智能变电站二次系统可靠性分析

唐志军， 李泽科 ， 陈建洪 ， 余斯航

(1. 国网福建省电力有限公司电力科学研究院， 福建 福州 350007; 2. 国网福建省电力有限公司， 福建 福州 350012)

0 引言

随着电子式互感器和高速以太网交换技术的发展以及IEC 61850通讯标准的实施， 智能变电站逐步取代了传统的变电站. 相比于传统的变电站， 智能变电站的设备更加精密， 结构更加复杂， 其继电保护系统的可靠性也降低， 增大了事故隐患. 而继电保护系统作为保护电网安全稳定运行的第一道防线， 其发生误动和拒动都会对人身安全和设备安全产生直接的影响. 对智能变电站的继电保护系统进行高效、 准确的可靠性评估并建立一套准确有效的可靠性评估体系， 有助于电力行业更加科学地建设智能变电站并对其进行有效的保护[1-2].

目前， 已有相关文献对智能电站二次系统的可靠性分析展开研究. 文献[3]以功能失效概率作为二次系统的可靠性， 依据功能图评估系统的风险并计算该系统的失效概率. 文献[4]则从各组件的故障概率出发， 计算不同功能配置的保护系统的故障概率， 并基于功能分解与二次设备之间的拓扑联系构建可靠性分析模型， 提出了保护系统整体失效、 拒动和误动概率的计算模型. 文献[5]从数字化变电站极点保护系统构成的特点入手， 提出一种将保护系统分为采样子系统和跳闸子系统的可靠性分析方法， 并分析了不同网络结构下二次保护系统的可靠性. 文献[6]考虑了二次系统的故障区段定位、 网络自动重构等功能特点和二次系统自身故障的影响， 提出智能配电网一、 二次综合系统可靠性的评估方法. 文献[7]运用可靠性框图法构建智能变电站继电保护系统完备的模型并对该系统的可靠性进行量化分析， 以长期稳态概率作为可靠性指标， 同时对“直采直跳”模式进行灵敏度分析， 评估出风险较高的元件或环节, 该分析包括概率灵敏度和元件灵敏度.

上述文献从不同角度或采用不同的方法对二次系统进行了可靠性分析， 但他们都是假设每套主保护的保护设备之间是相互独立的， 实际工程中， 同一套主保护存在多个不同设备共用一套电源的情况， 当电源回路中的设备出现故障时， 会对开关电源的滤波电容以及输出电压纹波造成影响， 从而影响同一供电回路中其他设备的正常运行， 所以同一套主保护的部分设备之间不是遵循严格独立的原则， 是具有相关性的[8]. 故对二次系统进行可靠性分析时， 考虑同一套主保护中的部分设备之间的相关性是非常有必要的[9]. 同时， 因为工作负荷与运行情况不同， 以及受到用户设备更换频率、 维护管理能力、 操作员技术水平、 现场环境等众多因素的影响， 具有相关性的设备之间的相关程度也随着场景的不同而不尽相同[10]. Copula理论最早应用在金融和水文领域数据分析[11]， 目前， 在电力潮流计算[12]、 MMC可靠性分析[8]、 风电场随机模拟[13]等电力领域已经得到应用， 因此， 本研究借助Copula理论中主要载体——Copula函数, 重点分析智能变电站中考虑不同设备之间相关性的二次系统可靠性.

1 智能变电站的结构及可靠性建模

1.1 智能变电站的结构

相比于传统的变电站的二次系统， 智能变电站的二次系统不但加强了信息的自动采集、 测量、 保护、 控制等功能， 还加入了电网实时自动化控制、 在线分析决策、 智能调节等高级功能[14]， 其拓扑结构如图1所示[15].

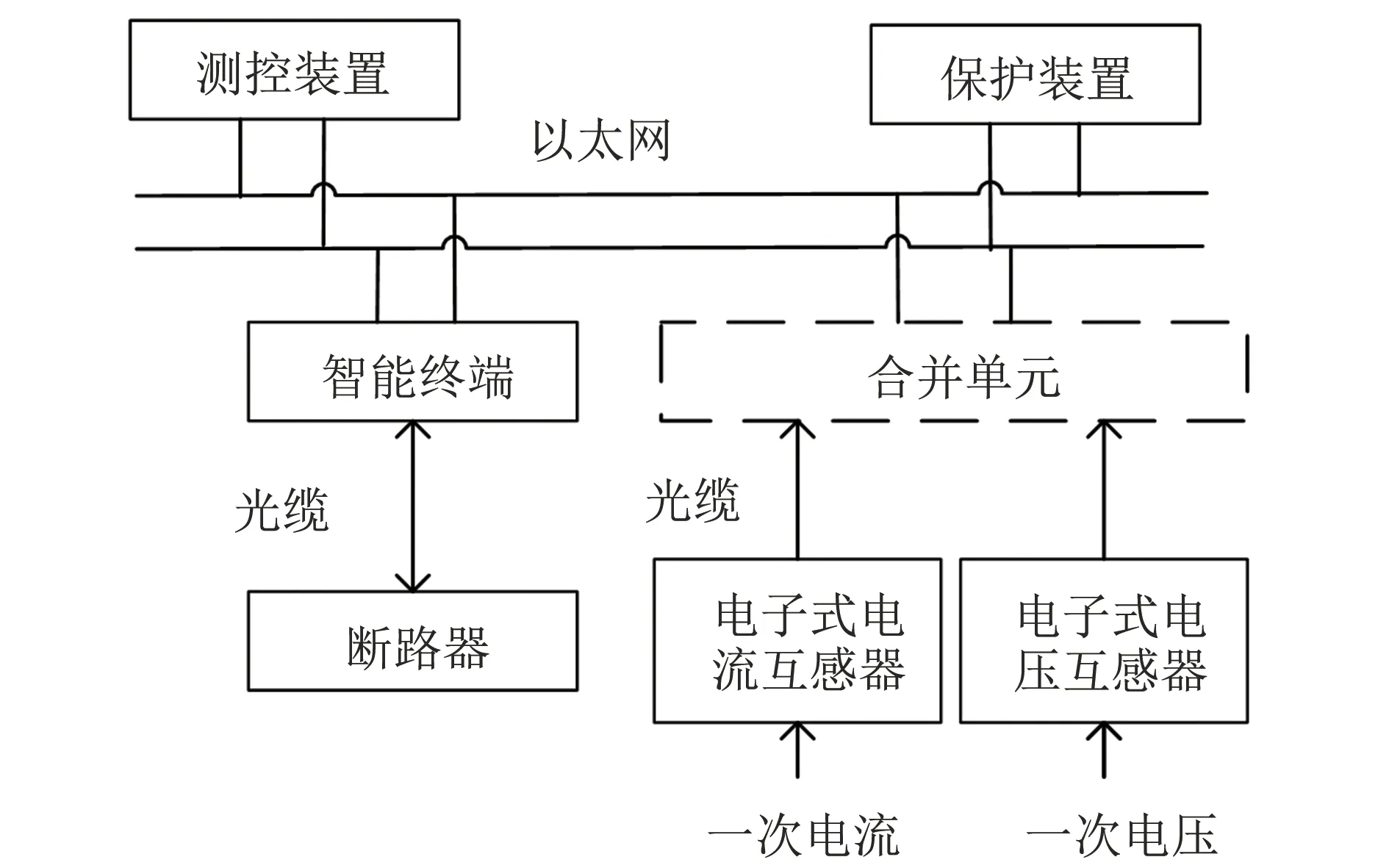
图1 智能变电站的继电保护系统Fig.1 Relay protection system for intelligent substations

智能变电站相比于传统的变电站， 站内所含关键设备明显增多， 且更加精密. 如图2所示， 站内所包含的设备都可以分为3个模块： 主机板、 电源模块、 网络接口， 然后这些设备经连接线连接起来构成设备链.

图2 设备链的组成图Fig.2 Composition of the equipment chain

在考虑智能变电站二次系统可靠性时， 每个设备的电源、 主机板、 连接线及网络接口的可靠性都将影响整个系统的可靠性. 如何对智能变电站继电保护系统进行准确的可靠性评估， 发现系统中的薄弱环节并加以改正或预防， 一直是继电保护工作面对的问题和研究的重点[16].

1.2 二次设备的可靠性建模

假设所有器件或者设备仅有正常运行和故障两种状态， 则可以用一个非负的随机变量X来描述其寿命， 则随机变量X相应的分布函数为

F(t)=P{X≤t} (t≥0)

(1)

积累分布函数F(t)的物理意义是器件的使用寿命小于等于t的分布函数， 那么可以求出器件在[0,t]时刻内正常运行的概率， 即系统的可靠性函数R(t)为

R(t)=P{X>t}=1-F(t)

(2)

假设系统中器件的故障率为λ， 且器件均处于寿命曲线的稳定运行区域内， 那么其可靠性函数将服从指数分布， 即在任意t时刻该器件的可靠性为

R(t)=e-λt

(3)

2 基于Copula函数的设备相关性建模

目前二次系统的控制保护屏柜均采用专门的开关电源模块， 用来将110～220 kV的公用直流电源变换为可以供给装置内部各组件使用的3.3～24 V低压直流. 由于直流电源所采用的电解电容在高开关频率下损耗严重， 输出的纹波会随时间增大， 滤波的效果也会随时间下降[17]， 当由开关电源供电的某个设备故障时， 必定会对开关电源中的电解电容造成不可逆的影响， 加速开关电源的老化并增大电源模块输出的电压纹波， 当电源模块输出的电压纹波大到一定程度时， 会对开关电源板卡模块的运行产生显著的不良影响[18]， 并进一步对同一供电回路的其他设备的可靠运行产生影响.

根据上述分析可知， 在同一套供电回路中， 电源或某个设备发生故障时， 其他设备也会受到影响， 所以这些设备就不遵循相互独立的原则， 而具有相关性. 在进行系统级的可靠性分析时， 考虑设备之间的相关性具有一定的意义. 由于不同设备之间具有相关性， 且这些设备之间的相关性不能用简单的线性函数来表示其相关系数， 所以文中采取一种比较灵活、 稳健的非线性相关性分析工具——Copula理论[19].

任何一个多维联合分布函数都可由若干个边缘分布函数以及描述相关结构的Copula函数来表示. 为了最大限度地反映信息量间的相关性和最简洁的结构， 可从多个候选Copula函数中选择生成元为φ1/(1-θ)(t)=(-lnt)1/(1-θ)的Gumbel-Copula函数对智能变电站的二次系统进行可靠性分析[9, 13].N维Gumbel-Copula函数为：

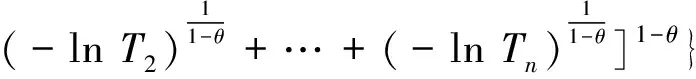
(4)

式中：θ∈(0, 1) ,θ=0表示所有设备均独立，θ=1表示所有设备均完全相关.

令F(T1,T2, …,Tn)为具有边缘分布F1(T1)，F2(T2)， …，Fn(Tn) 的N维联合分布函数， 由Sklar定理[20]知， 会存在一个Copula函数满足：

C(F1(T1),F2(T2), …,Fn(Tn))=P(T1≤t,T2≤t, …,Tn≤t)

(5)

若F1(T1)，F2(T2)， …，Fn(Tn) 是连续函数， 则这个Copula函数是唯一确定的.

当同一供电区的n个设备中电源模块使用寿命最短的设备发生故障， 此时会导致位于顶事件的保护系统不能正确动作.在t时刻， 位于同一供电区的设备可靠性等于寿命最短的设备使用时间X大于t， 即该供电区内所有的设备使用寿命X1,X2, …,Xn均大于时间t， 由加法公式得该供电区的可靠性函数为R(t)=P(X>t)=P(X1>t,X2>t, …,XN>t)

(6)

根据Copula理论， 存在N维Copula函数Cn[F1(X1),F2(X2), …，Fn(Xn)]， 使得

Cn[F1(X1),F2(X2), …，Fn(Xn)]=P{Xi1≤t,Xi2≤t, …，Xn≤t}

(7)

同时， 由于每个设备电源的分布函数为同分布， 所以求和符号里面的公式不用加以区别， 令p表示每一项求和运算的次数. 故可以得到一个供电区的可靠性函数为

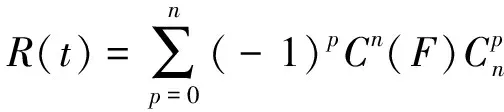
(8)

式中的F=(F1,F2, …，Fn) ， 因为Fi(∞)=1， 所以Fi=Fi(t)或1.

CN(F)=CN[F1(X1),F2(X2), …,FN(XN)]

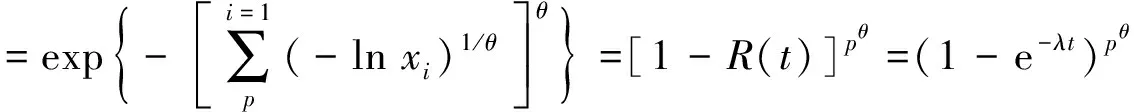
(9)

故可以得到一个供电区的可靠性函数为

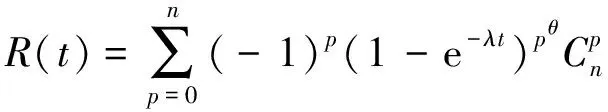
(10)

3 二次系统的可靠性分析

由1.1节可知， 组成故障链的设备都可以分成主机板、 电源模块、 网络接口3个模块， 这些模块和继电保护系统的失效关系如表1所示. 用λzj、λzw分别表示主机板的拒动故障率和误动故障率.故主机板的拒动可靠性Rzj(t) 、 主机板的误动可靠性Rzw(t) 分别可以表示为：

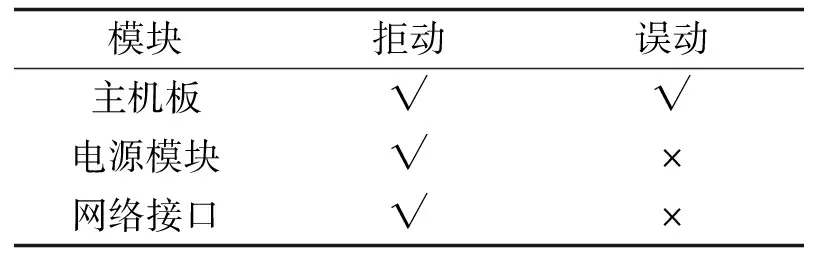
表1 模块失效分析表

(11)

由Copula函数可推导出电源模块的可靠性函数为：

(12)

则该设备的拒动可靠性函数为：

Rj(t)=Rzj(t)Rs(t)

(13)

因为电源模块和网络接口与系统的误动无关， 所以该设备的误动可靠性函数即为主机板的误动可靠性函数：

Rw(t)=Rzw(t)

(14)

由此可知， 当一条故障链由n个设备连接而成时， 除了这n个设备， 还会有n-1条连接线将这些设备连接起来， 设第i条连接线的可靠性为Rli(t) ， 则该故障链的拒动和误动的可靠性模型分别为：

拒动可靠性函数：

(15)

故障链误动的前提是要保证电源模块、 网络接口以及连接线可靠， 因此故障链的误动可靠性函数：

(16)

因为每个设备的分布为同分布， 所以求积公式里面的可靠性函数可不加以区分， 则式(15)、 (16)分别可简化为：

RJ(t)=[Rj(t)]n×[Rl(t)]n-1

(17)

Rw(t)=1-{[1-(Rw(t))n]×(Rs(t))n(Rl(t))n-1}

(18)

因此， 可以算出第m条故障率的整体可靠性为：

Rm(t)=RJ(t)RW(t) (m=1, 2, …,n)

(19)

220 kV及以上的智能变电站的二次系统中， 共有两套独立的主保护[21]， 而一套主保护又包含n条故障链， 则可以推导出其中一套主保护的可靠性为：

(20)

第二套主保护的可靠性的计算方式与第一套完全相同， 记为RB(t)， 则二次系统整体的可靠性函数为：

R(t)=1-[1-RA(t)][1-RB(t)]

(21)

4 算例分析

在实际工程中， 二次系统中继保设备的可靠性较高， 实际测得的可靠性数据不完备， 通常采用过裕量设计来提高系统的可靠性， 而其宗旨是提供一种可靠性的计算方法， 为二次系统的可靠性设计以及为维修策略的制定提供指导意义， 下面通过仿真模型来验证该方法的有效性与准确性.

设备中不同模块的故障率λ是个重要的已知参数， 结合已有文献的相关数据[5, 22]， 算例中主机板拒动的故障率选取为0.000 1、 主机板误动失效的故障率选取为0.000 1、 电源模块的故障率选取为0.002 5、 网络接口与连接线的故障率选取为0.000 8. 同时， 设备之间的相关程度受现场环境的影响而不能选取确定的值， 本算例分析考虑的相关程度范围为： 从0.1～0.8. 将从单条故障链、 故障回路的长度和故障回路中供电电源的数目3个方面分别分析系统可靠性变化的趋势.

4.1 单条故障链对系统可靠性的影响

为验证单条故障链对系统可靠性的影响， 根据式(21)绘制三维曲面(如图3所示)， 其中运行年限选择20 a， 相关系数取0.1～0.8. 取图3中的部分数据绘制出表2.

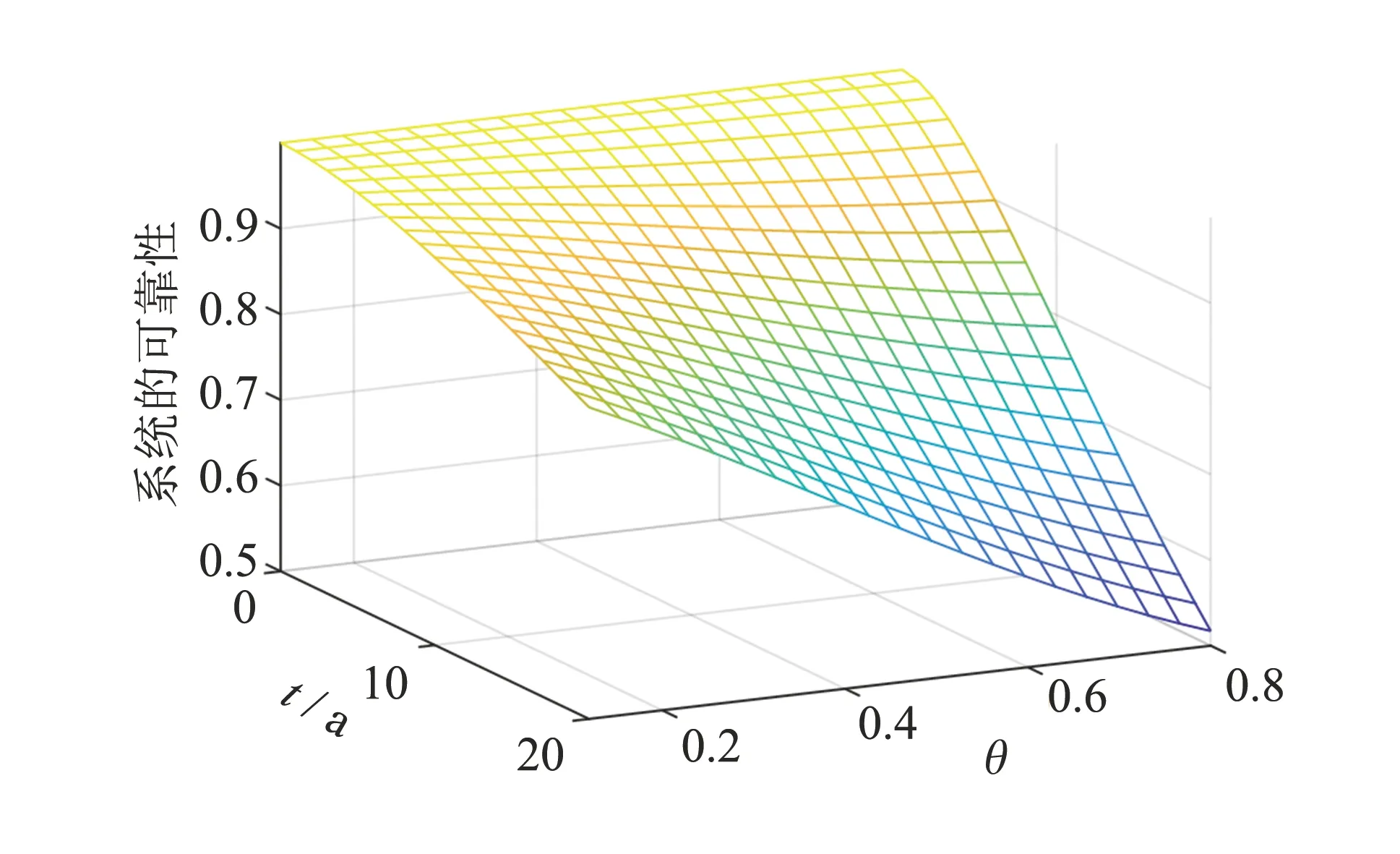
图3 系统可靠性曲线Fig.3 System reliability curve

表2 系统的可靠性

由图3和表2可以看出， 随着系统运行年限的增加， 系统的可靠性会迅速降低， 当设备运行年限达到15 a时， 系统的可靠性已小于0.9， 二次系统的可靠性已经不能满足智能变电站对可靠性的要求. 同时， 随着相关程度变大， 系统的可靠性也越低.

本文重点是研究各设备之间的相关性， 因此取运行年限为20 a， 相关系数从0.1～0.8， 分别绘制出相关程度、 运行年限的二维曲线簇进行分析， 系统可靠性随着运行年限、 相关程度变化的示意图如图4所示.

从图4(a)可以看出， 系统的可靠性随着相关程度的增加而减小， 运行年限越久， 受相关程度影响的系统可靠性下降速度也越快， 从图4(b)可直观地看出， 随着相关程度的增大， 不同运行年限时的系统可靠性之间的差距也越来越大； 在运行年限达到20 a时， 相关程度每相差0.2， 系统的可靠性数值已经相差0.1左右. 因此时间和电源模块之间的相关性对系统的可靠性影响不容忽视.

图4 系统可靠性变化示意图Fig.4 Change in system reliability

4.2 故障回路的长度对可靠性的影响

除了图3和表2中涉及到的相关程度和运行年限， 根据式(10)可看出， 具有共同相关性的设备的数目也会对系统的可靠性产生影响. 这里取具有共同相关性设备的数目个数为1至10， 相关程度取0.4， 绘制一组不同运行年限的二维曲线簇. 同时， 选取具有共同相关性设备的数目个数为1至10， 运行年限为15 a， 绘制一组不同相关程度的二维曲线簇， 系统的可靠性随共同相关性的设备数目变化如图5所示.

图5 系统可靠性随设备数目变化示意图Fig.5 Schematic diagram of system reliability varying with the number of equipment

由图5可知， 当1至4个设备存在相关性时， 系统的可靠性会急剧下降， 当具有共同相关性的设备超过4个时， 系统的可靠度已经降低到0.5以下. 因此， 同一条跳闸回路上， 共用同一供电回路的设备数目不宜超过4个， 而随着电网电压等级越来越高， 智能变电站的结构越来越复杂， 跳闸回路上设备的数目增加是必然趋势， 因此同一套主保护中应增加供电电源的数目来提高二次系统的可靠性.

4.3 考虑电源数量对系统可靠性的影响

分析同一套主保护中采用两套共用电源时系统的可靠性. 两套供电回路分别命名为A、 B回路， 分别对主保护中的部分设备进行供电. 定义情况①： 一套主保护中仅含有A套供电回路； 定义情况②： 一套主保护中含有A、 B两套独立供电回路.

这里取一条跳闸回路上的设备数目为5个， 其中A回路包含3个设备， B回路包含2个设备， 运行年限取0至20 a， 相关程度取0.1至1.0. 将采用A、 B两套供电回路与只采用一套供电回路的可靠性随运行年限、 相关程度变化的三维曲面绘制出如图6所示.

从图6可看出， 采用A、 B两套回路供电的情况②比只采用A供电回路的情况①的可靠性更好， 并且随着运行年限的增加， 系统的可靠性受设备间相关程度的影响越来越显著， 此结论与金融领域的尾部相关性原理相吻合， 证明该可靠性模型具有一定的合理性.

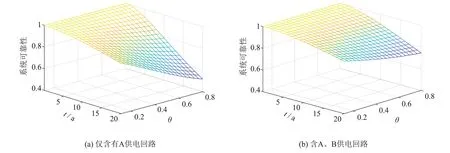
图6 系统可靠性三维曲面图Fig.6 Three dimensional surface of system reliability

为进一步验证采用A、 B两套供电回路对系统可靠性的影响， 绘制出系统可靠性随运行时间变化曲线， 如图7所示.

图7 系统可能性随运行时间变化曲线Fig.7 Curve of system possibility versus running time

从图7可看出， 随着运行时间的增加， 二次系统可靠性降低的速度也在加快； 在同一相关程度下， 情况②的可靠性比情况①的可靠性高， 且相关程度越大， 差距也越显著； 同时， 选取相关系数为0.5， 不同运行年限下的可靠对比见表3， 从表3可看出， 在同一相关程度下， 运行年限越长， 采用两套电源的可靠度提升越明显.

表3 两种情况下的可靠性对比

从图7也可以看出， 在情况①下， 系统的可靠性随着运行年限变化时， 不同相关程度下的系统可靠性差距比较大， 而在情况②下， 系统的可靠性随运行时间变化受不同相关程度的影响较小. 综上所述， 在一套主保护中， 采用两套或多套独立供电回路， 可以显著提高系统的可靠性， 而且随着相关程度越大、 运行时间越长， 这种可靠性提高的效果也越显著.

5 结语

1) 一条故障回路中， 不同设备之间的相关性对系统的可靠性有着显著的影响， 随着相关系数从0.1增至0.8， 系统的可靠性也从0.88降至0.52.

2) 缩短故障链的长度或者增加故障链中供电回路的数量可以大大提高二次系统的可靠性， 当相关系数同取0.5时， 随着运行年限的增加， 采用两套供电回路对系统可靠度的提升效果也从2.14%增加至13.43%.

3) 随着变电站越来越智能化， 变电站的二次系统会越来越复杂， 故障链长度的增加是必然趋势， 所以可以通过增加一套保护中的供电回路的数量来提高系统的可靠性.