太赫兹波段的taper型多模干涉耦合器
2021-12-31张宏祥谢静雅
张宏祥,谢静雅
(上海理工大学 光电信息与计算机工程学院,上海 200093)
引 言
多模干涉耦合器的自映像理论最早可以追溯到1836年Tabolt提出的自成像现象[1]。1973年,Bryngdahl[2]首次提出了在平面介质波导中实现自映像的可能性。随后,Ulrich等[3]用模式分析法首次解释了多模干涉的成像原理与规律。Bachmann等[4]给出了基于N×N多模干涉器的自映像理论。Lucas等[5]设计出基于多模干涉自成像原理的理论模型。近年来,关于低损耗,小型化的多模干涉耦合器的报道也越来越多[6-8]。2009年,Jiao等[9]提出了一种基于级联多模干涉(multimode interference, MMI)波导结构的偏振分束器,该偏振分束器为条形波导结构,其下包层为二氧化硅材料,可以实现TE/TM波的偏振分束输出。但该偏振分束不可对偏振态进行动态调控,并且存在光损耗较大、器件尺寸较大且不易于集成等缺点。
2012年,上海微系统所Sheng等模拟仿真了不同宽度的低损耗多模干涉器,并在实验测试中得到在1 530~1 570 nm波段的损耗低于0.1 dB的器件,该器件的大小只有3.6 μm×11.5 μm[10]。2013年,Zhou等设计出了基于绝缘体上硅的不同宽度的1×2的3 dB多模干涉耦合器[11-13]。
矩形MMI耦合器已有大量的研究成果,然而随着多模干涉区宽度的增加,MMI耦合器的长度会迅速增加,而集成光学的快速发展对器件的集成性要求也越来越高,Taper型MMI耦合器相对于传统的矩形MMI耦合器能有效地解决该问题。目前,多模干涉耦合器主要应用在通信等频段,并且是基于成熟的半导体加工工艺平台实现的。本文提出在太赫兹波段利用高阻硅(材料折射率为3.42)实现多模干涉耦合器,其中taper型在本文中指的是非矩形、逐渐变窄的结构,如椭圆形、抛物线型、锥型。该器件的实现为以后太赫兹波段的波分复用提供了思路。
1 MMI的理论分析
对于一个N×N的MMI来说,其成像原理是基于多模波导的自映像效应。可以简单地表述为:对于任一输入光场,在多模波导中沿光场传输方向上将周期性地出现输入光场的一个或者多个像的效应。目前对多模波导的场分布进行分析的方法诸多[14-17],对于MMI器件,主要采用模式传输分析法来实现模场分析[18]。
在平板中存在两种模式,一种为横电模(TE),另一种为横磁模(TM)。两种模式的区别在于电场和磁场的偏振方向。本文采用的是TM模式,TE模式推导类似于TM模式。图1为一多模波导的示意图。其中多模波导的宽度为Wm,波导芯层和包 层的折射率分别为n1和n2,此多模波导的输入波长为 λ0时,支持m个波导模式传播,用v=0,1,···,(m−1) 表示多模波导中不同模式的阶数[19]。设横向的波数为kyv,第v阶模式的传播常数为 βv,通过色散方程[20]可以得到
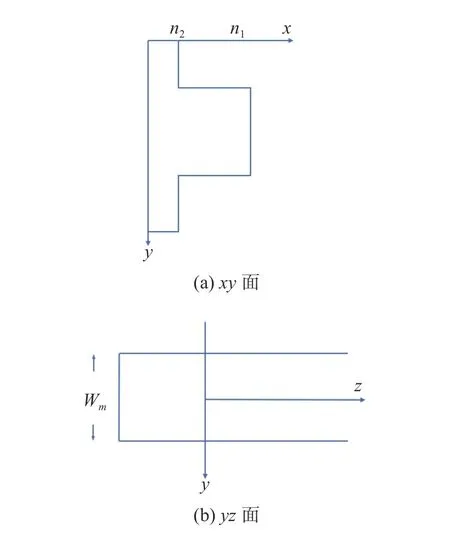
图1 多模波导的xy面与yz面示意图Fig.1 xy and yz dimensional diagram of a multimode waveguide
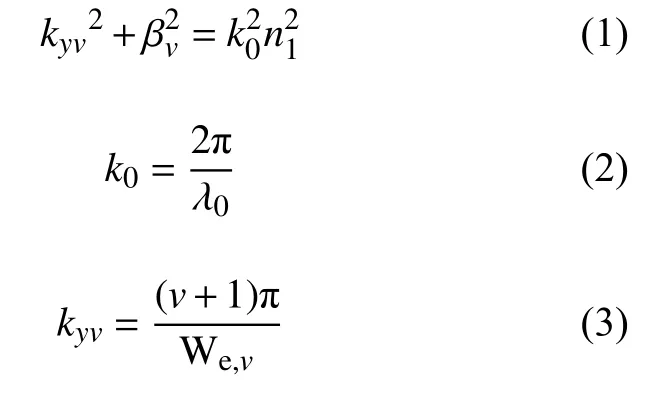
式中:n1为波导的折射率; We,v为第v阶模式的有效宽度。大多数情况下, We,v可以等效看成其基模(We)的有效宽度,表达式为式中 σ 代表极化因子,对于TE模式 σ =0 ,TM 模式 σ =1 。所以,最低二阶模式的拍长Lπ可表示为
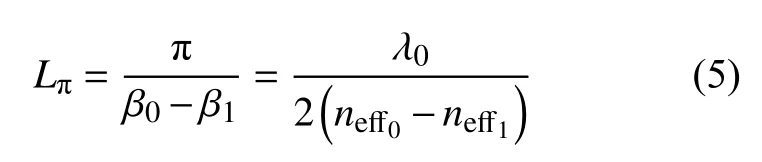
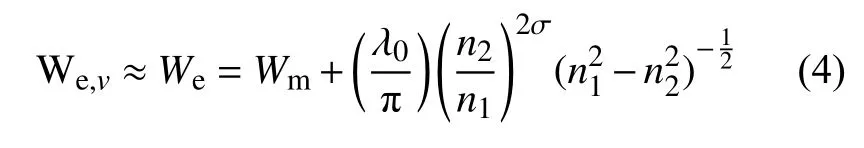
式中:neff0和neff1分别为对应的TE和TM模式的 有 效 折 射 率。假 设 输 入 光 场 ψ (y,0) 从z=0 处入射到多模波导,将其表示成所有模式场 ψv(y)的线性叠加,便可得到
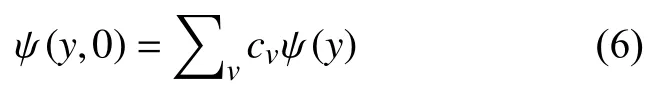
式(6)中的模式包含导模和辐射模,由于模式场成正交关系,则模式的模式激励系数cv可表示为

因为辐射模在实际的所有模式中的比例较小,可以忽略不计,只考虑导模,可以得出
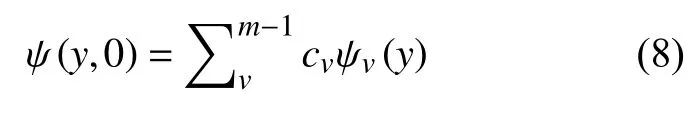
对于对称型1×N多模干涉耦合器,它的单个N重自映像位置满足
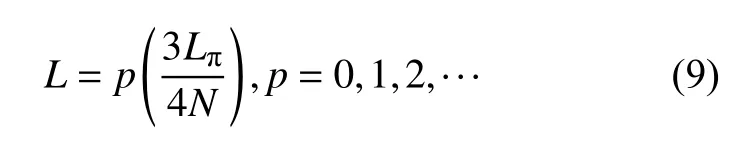
为了实现偶模激发,而奇模不激发,可以将输入的偶对称光场的位置(即单模输入波导的位置)选择在多模波导的中心位置,这样,自映像将会是多模波导中所有偶数阶模式的线性叠加。在实际的设计中,1×N的MMI通常用作N路光供分器,而考虑到器件的大小,通常将式(9)中的p值选择为1,即将MMI设计在第一个N重自映像的位置。
当选定一个合适的波导宽度W时,根据FDTD仿真软件可以计算得出对应的0阶和1阶模式的有效折射率,然后通过理论数值计算得到相应的MMI尺寸。
2 1×2 MMI的尺寸设计及优化
MMI主要是由单模输入输出波导和多模耦合波导三部分组成。硅基MMI就是以硅材料为波导介质。本文选取频率为185 GHz作为此器件的工作频率,波导厚度为340 μm,衬底厚度为130 μm。在这些工作条件下,光场能量能够很好地限制在波导中传输。
根据式(5)可知,如果想要设计一个MMI的具体尺寸,当确定宽度时,需要知道在该宽度的波导情况下,其对应的最低2阶模式的有效折射率。通过FDTD仿真可以计算出不同波导宽度下的最低2阶模式的有效折射率如图2所示。此处对多模波导进行选择时,通常是需要支持3个以上模式的,但是因为需要实现1×2的分光,器件结构如图3所示,所以要尽量避免激发过多的高阶模式即波导宽度不宜选择过大。通过Mode Solution仿真软件可以算出,当波导宽度小于1 600 μm时,不足以支持3个模式,所以本文选择的3个宽度分别为1 200 μm、1 400 μm和1 550 μm。首先,通过式(9)可以推算出多模波导的理论长度,然后在这个长度范围内通过FDTD软件进行扫参仿真优化。以1 200 μm为例,图4是它的光场分布,从图中可以看出,输入光场在多模波导区发生干涉叠加后,在输出位置几乎实现了均匀分光,上下功率分别为0.455和0.463。通过计算得出它的理论二阶拍长为3 744.5 μm,所以该多模干涉区的理论首个自映像位置约为1 404.19 μm,在这个数值范围内,进行200 μm的扫参优化,步进为10 μm,其结果如图5所示。结果发现,仿真的具体长度和理论计算有些偏差,因为在理论计算中,采用的是近似计算。
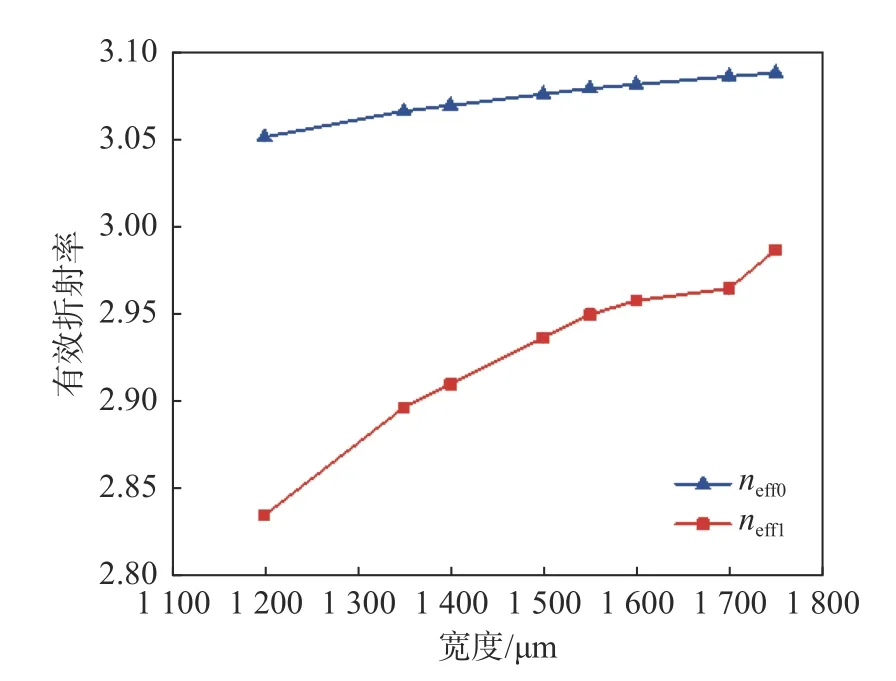
图2 有效折射率与波导宽度关系Fig.2 Relationship between effective refractive index and waveguide width
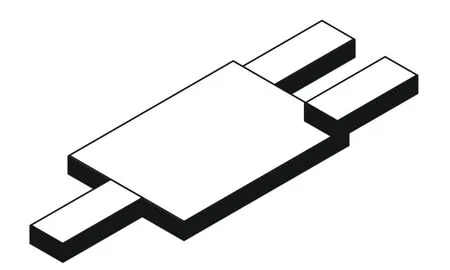
图3 1×2 MMI耦合器Fig.3 1×2 MMI coupler
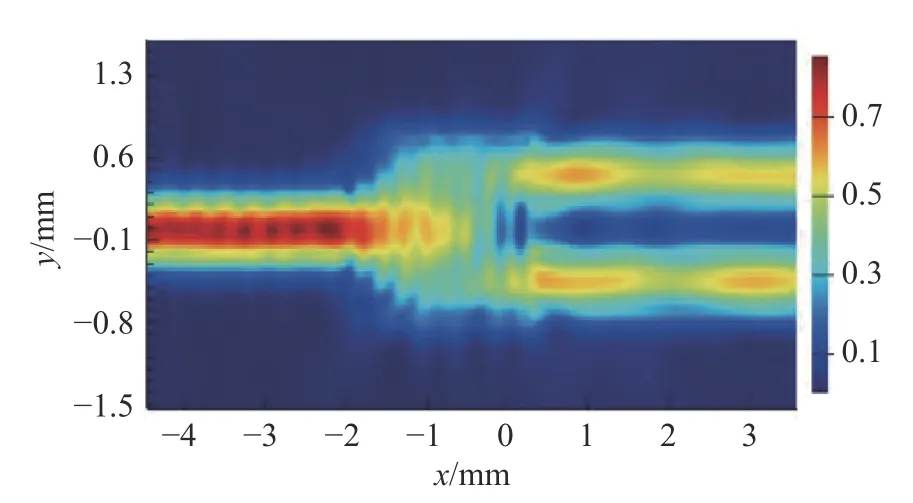
图4 MMI光功率分布Fig.4 Optical power distribution of MMI
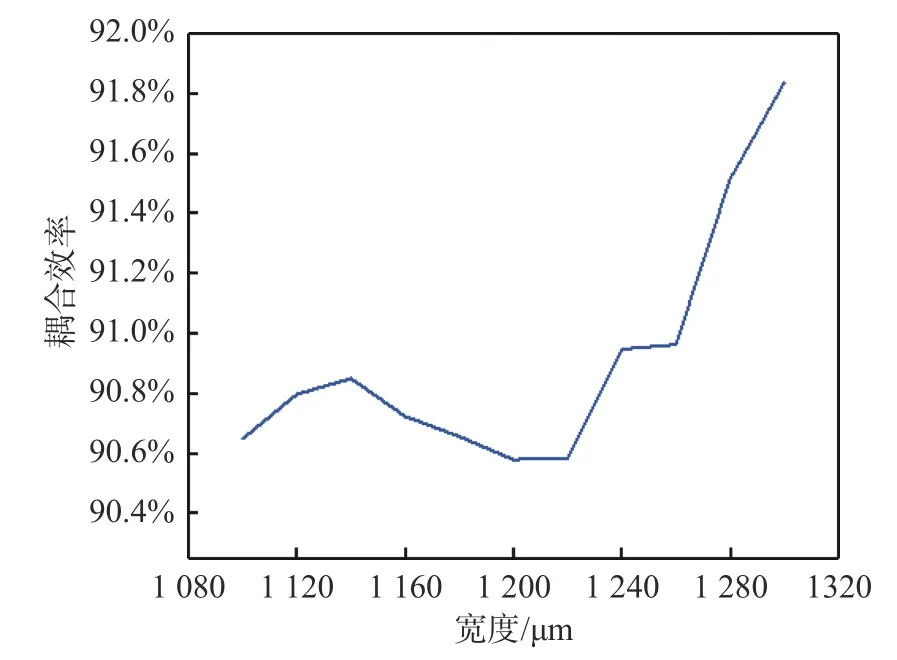
图5 不同长度的多模波导耦合效率Fig.5 Coupling efficiency of multimode waveguide with different lengths
同时,本文对其余两个宽度也进行了相同的仿真,结果如图6所示,从图中可以看出,当波导宽度为1 200 μm时,其耦合效率要高于其他两种情况,是因为选择的输入波导尺寸为500 μm的单模波导,多模波导的宽度增加会导致多模区和输入输出波导间的模式不匹配度增加[21]。
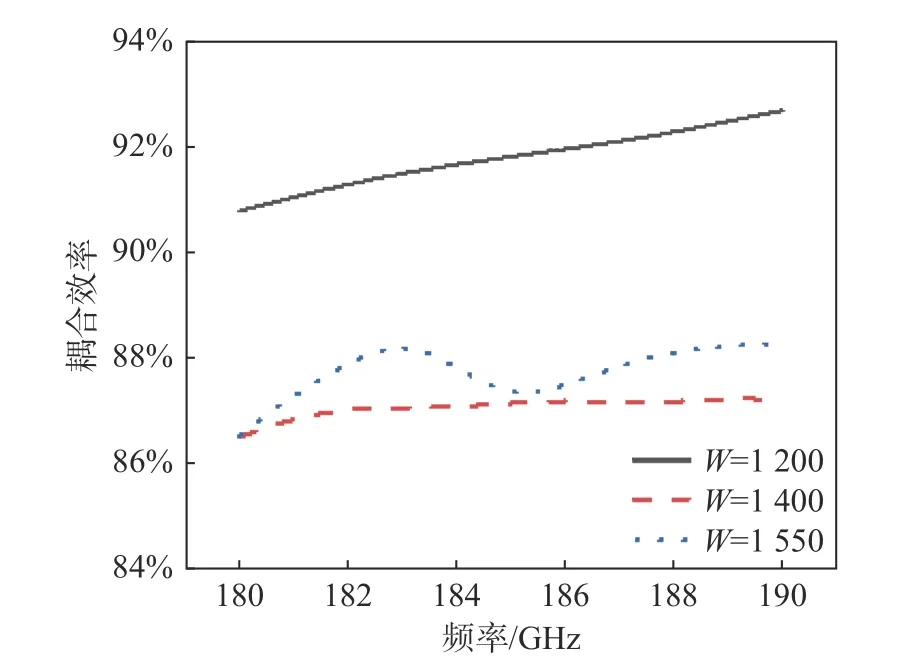
图6 不同宽度1×2 MMI的耦合效率Fig.6 Coupling efficiency of 1×2 MMI with different widths
上面对多模干涉区进行了尺寸优化,但是当输入波导进入多模波导区时,也会存在一个波导模式不匹配的情况,因为这里输入输出的单模波导的大小是固定的,所以需要给单模波导和多模波导之间添加一个渐变结构来缓解尺寸的突然变化,在此引入taper结构,如图7所示。这种线性taper的波导,能够减小单模波导和多模波导之间的模式转换带来的损耗,同时可以减小自映像的模式相位差,提高像的质量,从而减小MMI的损耗。当选取的工作频率为185 GHz时,保证两个taper的宽度不变,改变taper的长度,可以发现在taper长度改变的情况下,MMI耦合器的耦合效率受到的影响较小,且宽度较小的MMI对taper长度更不敏感。同时,在仿真设计中需要注意,Wt不能过大,不然会导致两个输出波导之间的间距G过小,工艺达不到。另外,还需要考虑taper的长度Lt对MMI的损耗影响。所以,最终选择Wt=550 μm,Lt=500 μm。通过taper结构可以有效地减小单模波导和多模波导之间的模式转换带来的损耗,提高耦合效率,从图8可以看出,在相同的宽度下,引入taper结构并不会改变它的耦合效率的趋势,而是整体上相对于没有taper结构的耦合效率数值的提升。与此同时,除了在单模波导和多模干涉区之间嫁接taper结构来减缓它的模式转换带来的损耗,还可以通过直接减小多模干涉区的体积,直接将多模干涉区做成taper型可以缩小整个器件的体积从而实现该多模干涉耦合器在集成光学中的片上集成,其结构示意图如图9所示。在该条件下,同样的1 200 μm宽度的多模干涉区,它的首个自映像的成像点位置为1 109.83 μm,即该多模干涉区的长度较之前缩小了很多,更加有利于该器件在集成光学中的应用,并且它能够获得和在单模波导和多模波导之间直接添加taper连接的结构相当的耦合效率,进一步实现了既减小了尺寸又提高了效率的目的,其耦合效率结果如图10所示。
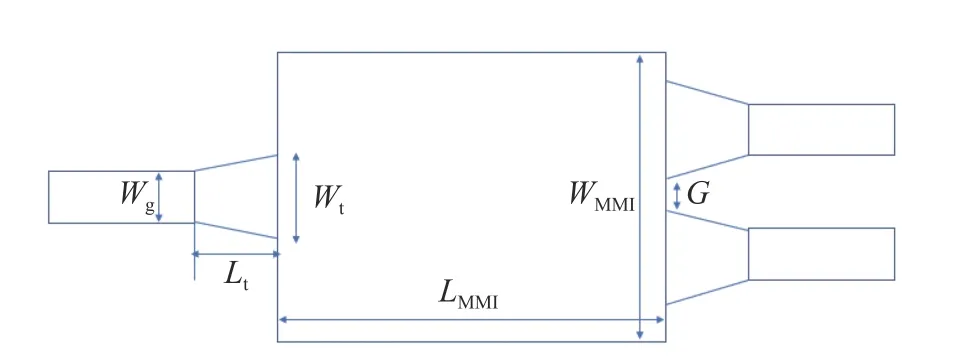
图7 Taper结构的1×2 MMI示意图Fig.7 Schematic diagram of 1×2 taper MMI

图8 有taper和无taper的耦合效率对比Fig.8 Comparison of coupling efficiency with and without taper
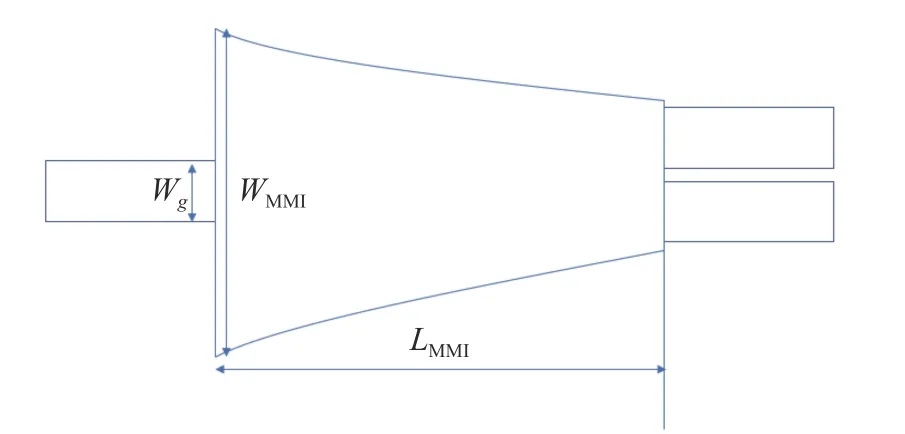
图9 Taper型多模干涉区Fig.9 Taper MMI area
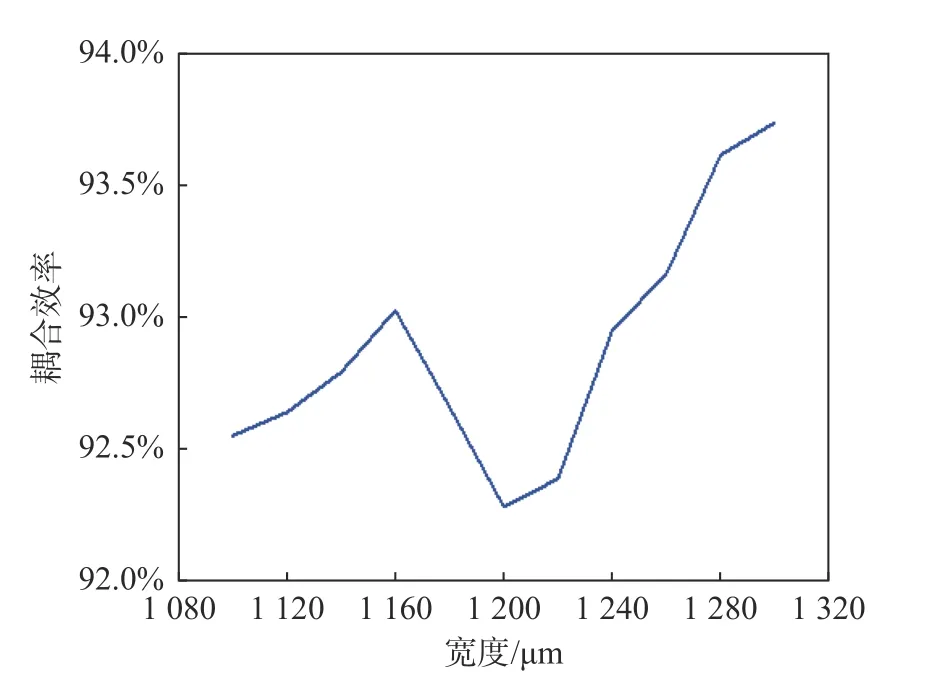
图10 Taper型多模干涉区的耦合效率Fig.10 The coupling effective of taper MMI area
3 结 论
本文通过多模干涉理论以及FDTD solution,Mode Solution仿真软件的结合使用,设计出太赫兹波段的1×2对称型多模干涉耦合器,并且通过理论推算它的二阶拍长,随后对它的宽度进行一系列的参数扫描优化得到了在185 GHz时,耦合效率较高的尺寸结构。同时也验证并改善了当多模波导宽度增大时,会使得多模干涉区和输入波导之间的模式不匹配度增加的问题。所以,在此基础之上提出添加一个taper渐变结构来减缓单模波导和多模干涉区之间因为模式的突然转换带来的模式不匹配从而导致多模干涉耦合器的耦合效率的降低,优化了基础的1×2 MMI的耦合效率,为之后的级联提供了思路。根据连接处的taper原理,提出是否可以将多模干涉区直接设计成taper型结构,以此达到在提高耦合效率的同时,做到缩小器件结构尺寸,为该器件以后的片上集成打下基础。且该器件是基于高阻硅材料设计的,有效降低了加工成本,为后面太赫兹波段的波分复用提供了思路。
