基于改进DE算法的并联泵组能效最优控制策略研究*
2021-12-30申林可徐金榜
王 丙, 申林可, 王 轩, 徐金榜, 苏 琴
(1.华中科技大学 中欧清洁与可再生能源学院,湖北 武汉 430074;2.中核兰州铀浓缩有限公司,甘肃 兰州 730065)
0 引 言
近年来,随着社会供水需求的不断提高,供水方式也渐渐发展了起来,变得更加灵活。变频供水接受的扬程和流量需求范围广,相比恒频供水更加节能而备受社会青睐,得以大面积推广。当前国内外的供水设备大多采用比例—积分—微分(proportional-integral-differential,PID)变频恒压供水方式[1],由于用户对流量和扬程的需求影响,以变频调速为主的多泵并联供水系统不断地发展。但目前许多的供水系统在运行时对水泵台数和转速控制的调度选择不当,导致系统运行的效率偏低,浪费电能。因此,多泵并联供水系统仍然存在较大的优化空间。若采用合理的优化调度方案,可以在满足供水需求的状态下,通过控制并联泵组系统中水泵的台数和调速率,同时约束水泵的运行效率,使整个系统运行能耗最优,达到节能的效果,获得一定的经济效益和应用价值。
差分进化(differential evolution,DE)算法具有对嵌入式MCU运算能力要求不高、收敛速度块、寻优能力强、鲁棒性强等显著特点。在工程项目中DE算法的优势显得尤为突出[2],不仅可以提供系统的运行效率,节约能耗;还可以降低产品的开发成本。DE算法走入供水行业的进程缓慢,因此,将DE算法用于解决并联水泵运行过程中的优化问题具有一定的研究价值。
1 供水系统的组成方式
多泵并联运行的供水系统,假设有m台同型号的水泵组成。管网与水泵连接,水泵的进水点为A,也是系统的分水点,系统的汇水点为B,Q1~Qm分别为每台水泵的流量,系统总流量为Qtotal。
2 供水系统的节能分析
图1中1为工频运行扬程流量曲线,2为变频运行扬程流量曲线,3为近似工况曲线,4为泵的效率曲线。水泵运行工况点的能耗需求为
(1)
在满足供水需求的前提下,变频供水相对工频运行下节省的能耗具体如下
(2)
式中 ΔHΔQ为图1中ABCD围成的图形的面积,在满足水力流量需求的情况下,变频控制的扬程更低,即更加节能。本文研究的是在变频节能控制基础上,通过约束水泵的运行效率,从而使系统能够节约更多的能耗[3]。
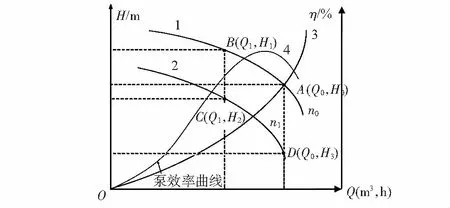
图1 单泵节能控制与效率曲线
3 供水系统的能耗模型建立
3.1 基本原理
水泵并联运行的总输入功率和效率是系统节能运行的重要指标。离心泵并联运行系统的全效率和输入功率的拟合关系式推导如下[4]
(3)
Pin(K)=
(4)
式中nt(K)为并联系统的全效率;Pin(K)为电网输入到水泵变频器的功率,kW。Hx,Sx,P0,α为水泵自身特性参数,分别为额定扬程、虚阻抗、额定功率和P-Q曲线近似斜率,H为水力需求的扬程值。则全效率nt(K)和功率Pin(K)可表示为自变量为调速率K的单值函数,分别记作η(K),P(K)。则供水系统能耗优化模型建立过程如下。
3.2 目标函数
minF=Pn1,n2=n1P(K1)+n2P(K2)
(5)
式中F为电网输入到泵组系统的总功率,n1,n2分别为当前投入的大小泵的数量。故系统优化的目标为泵组的总消耗功率,优化的相应问题也转换为:求取优化目标总功耗取得最小值下的n1,n2,K1,K2解,同时满足系统所涉及的下述所有的约束条件,以此提高运行效率,达到节约能耗的目的。
3.3 约束条件
1)流量约束
管网所需总流量为各泵实时流量之和
(6)
式中Qi min,Qi max分别为水泵流量高效区的最小值和最大值。
2)扬程约束
水力需求的扬程等于系统需求扬程减去管阻损失
(7)
式中Hi min,Hi max为水泵输出口压力的最小值和最大值,ξi为管网沿程阻力系数。
3)调速率约束
Ki∈[Ki min,Ki max]
(8)
式中Ki min,Ki max为水泵在高效区运行时转速的最小值和最大值。
4)水泵数量约束
n1∈[0,n1max];n2∈[0,n2max]
(9)
式中n1max,n2max分别为大泵小泵的系统装机数量。
4 系统能耗模型优化调度设计
4.1 适应度函数
适应度函数起着对种群优劣选择的作用。本文采用罚函数法对寻优过程中决策变量变化情况下的流量进行约束,保证Qr接近Qt时,泵组总功耗最小。惩罚项系数ε如下式所示
(10)
式中Qr,Qt分别为实际输出流量和需求流量,则相对应的惩罚目标函数可表示为
minF'(Pi(G))=minF(Pi(G))+ωε
(11)
式中Pi(G)为种群P的第i代个体,ω为权重系数。
4.2 DE算法改进过程
DE算法包括初始化、变异、交叉和选择等步骤。本文对DE算法的改进如下:
4.2.1 生成初始群体
3.1 缺乏统一管理机制 目前云南省现有的159个自然保护区,分属于多个系统进行管理,缺乏统一的管理机制,有的保护区同时也是风景名胜区、国家地质公园或其他的一些名称,不同的名称分属于不同部门进行管理,导致管理出现混乱的局面。
由于决策变量为整数,故对初始化后的变量需进行取整运算来增加种群的多样性,选择适应度优者作为初始种群中的个体。整数变量初始化如下
i=1,2,…,d1;j=1,2,…,D
(12)
式中 “[ ]”为向上取整或者向下取整。
4.2.2 变异操作
本文将DE/rand/1与DE/best/1两种变异操作结合,优势互补,产生新的变异方式[5]。群体中第i个向量个体,实数变量的变异操作如式(13)所示,对于整数变量的变异操作如式(14)所示
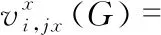
F(xr1,jx(G)-xr2,jx(G))
(13)
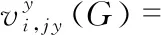
F(yr1,jy(G)-yr2,jy(G))
(14)

为保证DE算法在寻优过程初期与后期的寻优能力与收敛速度,加权系数根据算法寻优阶段来决定,以保证收敛性的权重越大。加权系数λ计算
λ=(Gend-G)/Gend
(15)
4.2.3 交叉操作
为了增加群体的多样性,交叉操作如下
(16)
式中 randij为(0,1)之间的随机小数,CR为交叉概率,CR∈(0,1)。
CR越大,试验个体从变异个体继承的比例越大,收敛速度越快,局部搜索能力越强;CR越小,试验个体从目标个体继承的比例越大,种群多样性越好,全局搜索能力越强[6]。所以,为保证群体寻优初期的多样性与寻优后期收敛速度,改进DE算法采用变CR的交叉方式,CR计算如下
CR=CRmin+G(CRmax-CRmin)/Gend
(17)
式中CR为当前交叉概率,其取值范围为[CRmin,CRmax]。G为当前种群迭代次数,Gend为终止代。
4.2.4 选择操作
为了确定xi(t)是否成为下一代的成员,试验向量vi(t+1)和目标向量xi(t)对评价函数进行比较
(18)
5 供水系统优化调度仿真
基于系统所建模型,使用MATLAB搭建仿真系统,仿真系统所涉及的水泵的参数如表1所示。
图2为不同水力需求下的优化过程。图3上为水力流量需求,下为需求与实际流量之间的偏差。图4上部分为
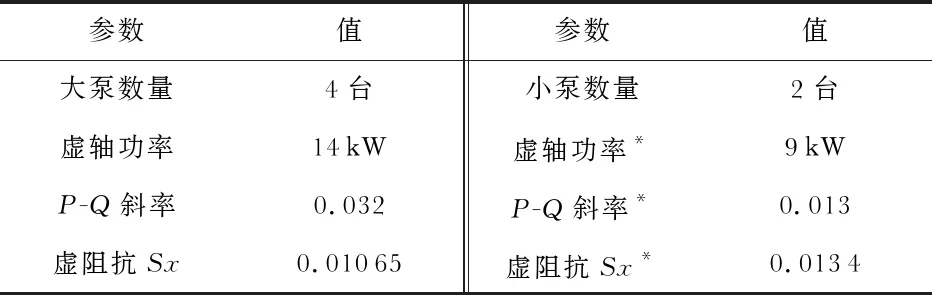
表1 系统仿真参数表
(备注:加*的为小泵参数)
不同水力需求下,系统需要投入的大小泵的运行台数,下部分为投入系统运行的水泵的调速率。仿真中,给定水力需求的扬程40 m(约合15层楼高),流量180 m3/h,即图3中0~500过程,待稳定后改变需求流量为135 m3/h,即图3中501~1 000过程,待稳定后改变需求流量160 m3/h,即图3中1 001~1 500过程。可以看出,在迭代约200次之后,收敛效果就愈发明显。说明DE算法对供水系统的水泵台数和调速率进行有效的优化控制,实现能耗的优化调度,如图4。
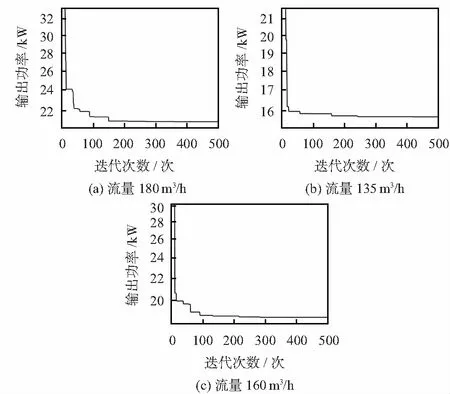
图2 扬程40 m不同水下流量寻优过程
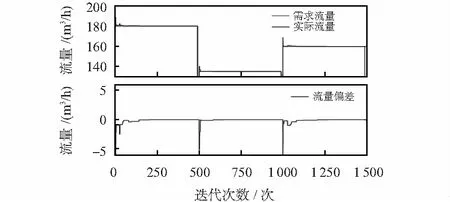
图3 流量状况分布

图4 大、小泵启动数量与调速率
为测试DE算法在需求流量突增突减状况下的动态和稳定性能,仿真设置在迭代次数达到500时,骤降流量为
135 m3/h,再次迭代次数到达500次时,突增流量为160 m3/h。图3,图4中可以看出,在突增突减流量时,DE算法能够快速准确地寻找出相对应的水泵及调速率组合,对并联泵组能耗有效的优化调度。
6 结 论
仿真结果表明:本文提出的DE算法能够很好地对并联泵组系统进行能效优化调度规划,同时在模拟需求流量目标突变状态下也显示出了良好的动态性能,证明了系统所建立模型的可行性和DE算法求解的有效性和鲁棒性。
