含空洞岩体微震定位的快速行进法——性能分析与工程应用

蒋若辰 ，戴峰 ,*，刘燚 ，李昂

a State Key Laboratory of Hydraulics and Mountain River Engineering, College of Water Resource and Hydropower, Sichuan University, Chengdu 610065, China

b School of Highway, Chang’an University, Xi’an 710064, China

1. 引言

地下空间开挖活动无可避免地引起工程围岩的应力重分布，进而诱发裂纹的产生与岩石断裂能的释放。作为一种有效的实时监测方法，微震（microseismic, MS）监测技术通过埋设于工程岩体内部的微震传感器，探测岩石破裂释放的应力波，并基于不同的地球物理反演方法，获取岩石破裂特征。这一监测技术，可对即将发生的地质灾害，诸如岩爆灾害，提供提前预警，并采用特定的实时支护措施来保证工程建设的安全[1-3]。当下，微震监测这项三维实时监测技术，已经被广泛地用于多个岩石工程领域，如矿业工程[4-6]、深埋隧洞[1,3]、岩质边坡[7-9]，以及地下厂房[10-12]。

微震震源定位是这项监测技术的重要部分，是其在工程项目中实现应用的基础[13,14]。对岩石工程中微震活动的解译，很大程度上依赖于微震震源定位的准确性。精确且快速的定位方法能够指引工程围岩裂纹网络分布圈定工作的进行。在获取定位结果的基础上，进一步的破裂源反演工作才能够进行，用于揭示围岩变形或者破坏模式，为岩石失稳提供提前预警，减少人员伤亡与设备损失。因此，微震破裂源定位是微震监测技术领域一个受到极大关注的课题。

在微震破裂源定位中，岩体波速模型的确定非常重要。在监测范围较小且岩性均一的情况下，均一波速模型能够保证微震定位工作快速稳定地实现，因而在岩石工程中得到了广泛引用。最早的基于数学计算的微震震源定位方法是所谓的Giger法，即将定位问题转化为求解基于微震信号到时的线性方程组[15]。在此之后，随着计算方法与技术的发展，基于这一思路的新方法得以提出与发展[16-18]。正如文献[19]所总结，这些经典的定位方法，诸如相对定位法和联合震源定位法，进一步提升了微震震源定位的准确性。然而，这些方法在运用到较为复杂的地质环境中，会造成相对较大的误差。

近年来，一些新方法被提出，用以满足受复杂地质环境影响的岩石工程项目中对微震震源定位的需求。Dong等[20,21]提出了多种应用于地下矿井的微震震源定位方法，诸如多步定位法与三维综合解析法。之后，Dong等[22]与Hu和Dong [23]基于A*搜索算法，提出了无需测速的微震/声发射定位方法，用于不规则复杂地质结构。Feng等[24]开发了分层波速模型，并系统测试了两种不同的方法对于微震震源定位的可行性，结果展示了所提出的方法能够减小平均定位误差[25]。Castellanos与Van der Baan [26]基于矿井中相似波形，提出了一种互相关的定位方法。Gong等[27]提出了一种应用于煤矿中的各向异性波速模型，与均一波速模型相比，该模型能够提供更准确的微震震源定位结果。此外，一些学者也将微震震源定位问题，转化为高维优化问题，并且采用等效波速模型来实现微震定位。这类方法会将额外的参数引入优化搜索过程，并且，启发式算法，诸如遗传算法[28]和重力搜索法[29]，也会被引入以获取微震破裂源与等效波速模型[30]。然而，在大跨度地下厂房建设中实现微震震源定位，仍然面临诸多挑战。首先，现有的方法无法实现在任意复杂的岩体波速模型中的定位。其次，地下洞室的开挖，特别是大型地下洞室的开挖，会在岩体中产生形状不规则的大空洞区域。简单的等效岩体波速模型无法解决这些问题，因此会干扰最终的定位结果。

本研究开发了一种新的微震定位方法，以实现在含空洞复杂岩体波速模型中的微震事件定位。建立了基于网格的岩体波速模型，其中不同的网格节点被赋予不同的纵波速度以反映复杂的岩体纵波波速分布。之后，二阶差分形式的快速行进法被引入，用于计算从破裂源产生的波到达各个节点的理论到时。基于现场采集的微震破裂信号，通过搜索理论到达时间与实际到达时间之间残差最小的最优网格节点，实现微震破裂源定位。本文所用的方法将在第2节中介绍，并且其性能表现将在第3节的一系列数值仿真实验中进行分析。猴子岩水电站地下洞室开挖过程中所采集的、具有代表性的爆破与微震事件将由本方法来实现定位，进一步展示本方法潜在的应用价值。本文第5节为主要的结论。

2. 方法

这一节将展示利用二阶差分形式的快速行进法计算理论到时的过程。一个目标函数将被用于计算理论到时与实际到时之间的残差值，进而实现微震震源定位。此外，线性插值法与龙格-库塔法将被用于获取从破裂源到微震传感器之间的传播路径。

2.1. 二阶差分形式的快速行进法

对于地下洞室的微震监测，P波到时通常被用于定位微震事件。在本文中，二阶差分快速行进法作为一种在离散区域内，采用有限差分方式，以网格为基础的实用计算方法，被用于计算P波理论初至到时[31,32]。这一方法能够有效地避免很多其他射线追踪方法（如打靶法[33]与弯曲法[34]）所固有的问题。在各向同性的介质中，P波的弹性波方程可表示为：

式中， 为标量势函数；v为P波波速；t为时间。式（1）的通解可被表示为：

将式[3]与式[4]导入式[1]中，可得式[5]：

式[5]的左侧包含了虚数项与实数项，但式[5]的右侧仅包含实数项。故可获得式[6]与式[7]：

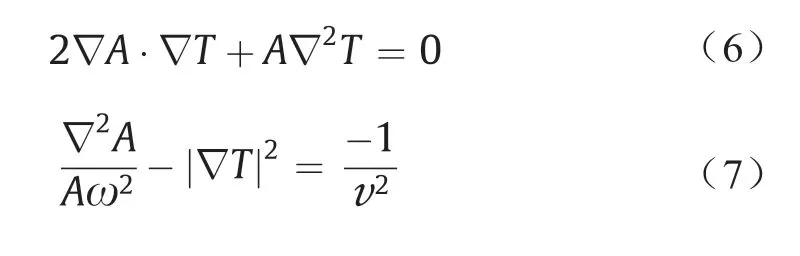
式[6]为传输方程，用于计算A。式[7]在“高频近似”假设的基础上，即时，可被简化为程函方程：

式中，T为P波初至到时；v为微震/地震波的P波波速，它们都是与位置(x,y,z)有关的函数。

目前，对于程函方程，虽然有一些数值解的方法，但是无法获得解析解。快速行进法将式（8）的微分方程形式转化为差分方程的形式进行求解，来获取P波初至到时T。原始的计算区域将被转化为离散的网格与节点。基于相关的地质调查数据，岩体与空洞区域相应的网格节点被赋予相应的P波波速值。Sethian与Popovici[35,36]，以及Chopp [37]进一步引入熵迎风格式（entropy satisfying upwind scheme）来处理梯度不连续问题，这使得快速行进法能够模拟P波传播。程函方程的差分形式可被表示为：

同理，相同的差分方式也可用于沿y轴与z轴的差分计算[图1（a）]。对二阶快速行进法而言，不同阶数的差分算子的使用依赖于二阶差分算子是否可用。如果网格节点的T无法获得，诸如靠近破裂源点与计算边界，那么二阶差分的计算形式将被转化为一阶差分的形式。

式（9）描述了在特定网格节点，采用差分的方式计算初至到时。这一计算过程在不同的待计算节点处的连续实施，需要正确地确定待计算节点的计算顺序，以保证与P波传播的方向一致。在快速行进法中，P波的传播可以使用窄带技术来计算从迎风区到下风区的初至到时，其概念如图1（b）所示。所有的网格节点被标记为激活点、近点与远点三类点中的某一类。激活点位于窄带的迎风区，其初至到时计算已经完成。近点位于窄带中，其初至到时采用式（9）获得了一个尝试值。远点位于窄带的下风区，并未进行初至到时计算。窄带的扩展过程首先搜索近点中初至到时尝试值最小的节点，将其标记为激活点，并将其周围的所有邻点中的远点标记为近点。之后，采用式（9）计算该新激活点周围的近点的初至到时值。窄带的形状可被视为P波传播的初至波阵面，并且上述计算过程不断重复，直到所有网格节点被标记为激活点，完成计算。

图1. 二阶差分快速行进法实现过程。（a）二阶差分形式示意图；（b）快速行进法采用窄带技术实现整体扩展。

2.2. 射线路径追踪

快速行进法有效地将P波传播简化为基于网格的射线追踪[32]。在获取计算区域内的所有网格节点的初至到时之后，从微震破裂源点到计算区域内的其他任意节点的传播路径（也就是射线路径），可以基于初至到时梯度来获得。如果将射线传播路径视作由多个直线段组成，并令rn(xn,yn,zn)为第n步计算之后的射线路径位置，则在射线路径上，下一步计算所达到的位置如下：

图2. 基于线性插值的方式计算到时梯度。

式中，h为网格间距。同理，B、E、F点的到时梯度可被表示为：

O点与D点的到时梯度可以用相同的方式表示为：

因此， 可通过如下计算获得：

为了获得更准确的rn+1，龙格-库塔法被用于计算式（12），其被转化为如下形式：

2.3. 定位方法

微震震源定位通过搜索理论到时与实际到时之间的最小残差来实现。假设诱发的微震事件发生在时刻t0，经过Δti的时长，在时刻ti达到第i个微震传感器，则对于第i个传感器的理论到时与实际到时之间的残差ξi满足如下关系：

式中，ti可通过提取在岩石工程中采集到的微震信号的实际到时而获得；Δti可用二阶快速行进法计算获得；而仅使用一个微震传感器，无法获得t0。为了消除t0对定位结果的影响，多个微震传感器被采用，并且不同传感器之间的残差可通过下式获得：

式中，ξi与ξj分别表示第i个与第j个微震传感器所对应的残差。虽然在理想条件下，ξi,j等于0，但在实际中无法实现（因受多因素的限制，如P波到时提取，以及Δti和Δtj的计算）。然而，相比于其他点，微震破裂源点的ξi,j的绝对值最小。因此，微震震源定位的实现可通过搜索节点，使得与其对应的多传感器的残差值最小。换言之，在给定波速模型中，首先使用二阶快速行进法计算所有网格节点到每一个微震传感器的Δt，之后微震震源点的确定，可通过搜索使得不同传感器的残差值达到最小的网格节点来实现。此处，我们基于最小二乘的思路，使用目标函数f来量化残差，如式（23）所示。

式中，(x,y,z)是波速模型中任意网格节点的坐标。微震破裂源点可使得目标函数f达到最小值。

至此，整个定位过程可被总结如下：

步骤1：建立波速模型，并对相应的网格节点赋予相应的P波波速值。

步骤2：使用二阶快速行进法计算所有网格节点到每一个微震传感器的理论到时。

步骤3：基于实际到时，计算目标函数值。

步骤4：搜索几个最小目标函数f值所对应的网格节点。其坐标的平均值被视作微震震源点的位置。在本文中，取10个最小目标函数值及其所对应的网格节点来实现定位。

步骤5：从微震破裂源点到每一个微震传感器之间的射线路径，通过2.2节中的方法获得。

3. 数值实验

本节将进行多组数值实验来展示二阶快速行进法和射线路径追踪的性能。此外，数值定位实验被用于验证定位方法的合理性。

3.1. 二阶快速行进法

在这一部分，将进行一阶与二阶快速行进法的对比实验，以展示初至到时的表现。所采用的波速模型为100 m × 100 m × 100 m（长×宽×高），网格间距为1 m。微震破裂源点位于(0, 0, 0)，并且所有网格节点的P波波速值为4000 m·s-1。两节点之间的距离除以P波波速，所得的值可作为两节点之间到时的解析解。数值解通过一阶与二阶快速行进法计算获得。此外，ξti被用于量化计算误差，其定义如式（24）所示：

式中，ξti为第i个节点处的误差；tNi与tAi分别为第i个节点处的数值解与解析解。

计算结果被展示在图3中。图3（a）展示了在波速模型中解析解的初至到时。计算误差被分别展示在图3（b）、（c）中。显然，由于采用了高阶差分的方式，二阶快速行进法有更好的表现，并且能够有效地减小计算误差。在图4中，盒形统计图被进一步用于量化计算误差分布。与一阶快速行进法相比，二阶快速行进法计算误差更小，且分布在较小的范围内。一阶快速行进法的误差中值（4.1 × 10-4s）是二阶快速行进法相应的误差中值（1.0 × 10-4s）的4倍，并且一阶快速行进法的下四分位数误差（3.15 × 10-4s）也明显大于二阶快速行进法。由此可见，二阶快速行进法能够获得更准确的计算结果。

3.2. 射线路径追踪

在这一小节中，建立一个双层波速模型与一个含空洞波速模型来验证基于二阶快速行进法计算结果的射线路径追踪方法的合理性。

图3. 一阶与二阶快速行进法在100 m × 100 m × 100 m的均匀波速模型中的计算结果。（a）解析解结果；（b）一阶快速行进法结果；（c）二阶快速行进法结果。

图4. 采用一阶与二阶快速行进法获取结果误差的盒形统计图。一阶与二阶快速行进法计算误差的离群值分别为9247和2701。Q1：上四分位误差值；Q3：下四分位误差值；IQR：Q3～Q1。

双层的波速模型网格间距为1 m，模型大小为200 m × 200 m × 200 m（ 长×宽×高），0～100.5 m高的P波波速为6000 m·s-1，101～200 m高的P波波速为4000 m·s-1。微震破裂源点位于(100, 100, 0)，并且10个微震传感器被安装，其坐标如表1所示。破裂源点与微震传感器之间的传播路径如图5所示。根据地震学的射线理论，在两个区域交界面上，射线传播应该满足斯奈尔定律（Snell law），如式（25）所示。

图5. 在两层波速模型中，从破裂源点到不同传感器的射线路径。

式中，θ1和θ2分别为入射角与折射角；v1和v2为两个区域相应的P波波速值。此处，v1和v2值分别取为6000 m·s-1和4000 m·s-1，故v1/v1=6000/4000=1.5。这里，Ri被用于量化射线路径计算误差，如式（26）所示。

式中，Ri对应第i个微震传感器的误差；θ1i和θ2i分别为第i个微震传感器所对应的入射角与折射角。在表1中，R的最大值不超过1.5%，且大部分R值没有超过1%，可忽略不计。可见，基于2.2节中的思路所获取的射线路径，在界面处满足斯奈尔定律。

表1 Ri的误差结果

图6展示了含空洞的波速模型，其尺寸为200 m ×200 m × 200 m（长×宽×高），网格间距为1 m。空洞区域的P波波速设为340 m·s-1，模型剩余部分的波速设为5000 m·s-1。空洞区尺寸为25 m × 65 m（半径×长度），圆柱中轴线经过(50, 35, 50)与(50, 100, 50)两点。三个微震破裂源点分别位于(45, 5, 50)、(45, 55, 95)、(70, 70,20)，四个微震传感器分别布置在(25, 45, 65)、(25, 45,35)、(75, 45, 65)、(75, 45, 35)。所获得的射线路径如图6所示。在离空洞较远的区域，射线路径沿直线传播，如同在均一波速模型中传播；而在靠近空洞的区域，射线传播路径紧贴空洞区外侧进行传播。这些结果展示了采用本文中的方法在含空洞区域依然能够获得合理的射线传播路径。

3.3. 数值定位实验

图6. 三个微震破裂源点到四个微震传感器的射线传播路径。（a）三维视图；（b）右视图；（c）前视图；（d）俯视图。

建立一个大小为383 m ×100 m × 121 m、网格间距为1 m并含空洞的波速模型，用于测试本文的定位方法（图7）。这一模型基于地球物理学领域的Marmousi模型所建立。三个隧洞模型沿Y轴平行布置，尺寸为15 m × 100 m（半径×长度），其中轴线分别过(75, 50,50)、(176, 50, 50)、(330, 50, 65)三点。由一阶快速行进法计算破裂源点到每个传感器的到时，将其视作从P波中提取的实际到时，即式（23）中的ti与tj。所有的理论到时，也就是式（23）中的Δti与Δtj，采用二阶快速行进法计算获得。微震震源定位基于式（23）实现，并且最终的定位结果为10个最小残差值对应的网格节点坐标的平均值（图7）。表2展示了所有的定位结果，这些结果相应的误差均小于4 m，表明该方法能够在较为复杂的波速模型中实现微震破裂源点定位。

表2 在数值定位实验中的定位误差

4. 在岩石工程中的应用

4.1. 工程项目简介

将本文的定位方法用于定位在猴子岩水电站建设期间开挖过程中所发生的爆破与微震事件。猴子岩水电站是典型的大跨度水电工程项目，该水电站建设在大渡河上，位于中国四川省成都市西南方约450 km。猴子岩水电站的地下厂房洞室群主要由主厂房、主变室、尾水调压室以及母线洞组成。三个主要的地下洞室（包括主厂房、主变室、尾水调压室）沿轴向方位北偏西61°（N61°W）平行布置，以高边墙大跨度为主要特征。主厂房的开挖规模约为219.5 m × 29.2 m × 68.7 m（长×宽×高），其最小垂直与水平深度约为380 m与250 m。主变室长141.1 m、宽约18.8 m、高约25.2 m，而尾水调压室长约60 m、宽约23.5 m、高约73.98 m。多种工程地质勘查结果表明，一些结构面包括小断层与层间错动带穿过工程开挖区[38]。最大主应力方向大致沿东西向，且地下厂房周围围岩主要为完整坚硬的变质灰岩[39]。更多关于工程项目与现场工程地质情况的详细信息，请参考文献[39]。

图7. 使用二阶快速行进法在含空洞复杂波速模型中的微震破裂源定位。

4.2. 微震监测系统构建

为了监测由于开挖所诱发的岩体中的微震活动，一套由加拿大Engineering Seismology Group（ESG）公司生产的高精度微震监测系统被安装在地下洞室中（图8）。ESG微震监测系统主要由paladin数字信号采集系统、Hyperion数字信号处理系统，以及多个微震加速度传感器所组成。所安装的微震加速度传感器的频响范围为50～5000 Hz，被布置在边墙上的钻孔末端，如图8所示。获取的微震信号通过Hyperion处理系统，以10 000 Hz的采样频率处理为数字信号。微震传感器的坐标分别为(41.70, 62.00, 1706)、(71.55, 62.20, 1706)、(97.80, 62.30, 1706)、(128.95, 56.80, 1703.5)。基于爆破测试与数字声波测试的联合反演结果，围岩P波波速为5239 m·s-1。监测信号数据通过ESG Wavevis软件以“.txt”的形式导出，使用Python进行处理分析。典型的微震波形通过本研究参与者手动识别提取，并采用赤池信息准则（Akaike information criterion, AIC）[40,41]进行微震信号P波的初至到时提取。

4.3. 开挖所诱发的微震活动

2013年12月5日至2014年1月16日，在主厂房与母线洞之间安装的ESG微震监测系统捕获了大量微震事件。在此期间，开挖活动采用钻爆法结合机械开挖的形式进行。图9展示了在采集微震监测数据之前，所完成的开挖的区域。开挖所诱发的微震事件主要分布于主厂房的下游边墙一侧，位于2#与3#母线洞之间。基于均一波速模型的定位结果被获取，该结果忽略了空洞区域（即开挖区域）的影响。结果，一些微震事件被定位于空洞区域（图9），这对开挖损伤区的圈定造成消极影响。

4.4. 基于二阶快速行进法的微震事件定位

4.4.1. 含空洞复杂波速模型构建

地下洞室的含空洞波速模型由图10所示的方式建立。首先，采用三维设计软件（如Blender和AutoCAD）建立三维洞室模型，并且根据工程项目进展，确定计算区域，确保模型包含所有的空洞区域。建立笛卡尔坐标系，如图10所示，使得Y轴方向平行于所有洞室的中轴线，并且Z轴的方向垂直向上。整个计算区域大小为162 m × 220 m × 86 m [图10（a）]，并且被划分成网格间距为1 m的正方体网格。所有网格节点的坐标被记录，并且基于现场爆破与声波测试联合反演的结果，将整个计算区域的P波波速设为5239 m·s-1。接下来，进行布尔运算（Boolean operation）以获取开挖区域与整个区域的交集区域[图10（c）]。之后，交集区域的节点三维坐标被获取，并依据对应的坐标，将空洞区节点的波速修改为340 m·s-1。

图8. 猴子岩水电站地下洞室群布置及ESG微震监测系统现场构建。

图9. 2#和3#母线洞之间的微震事件基于均一波速模型的定位结果。（a）微震事件的三维空间分布；（b）俯视图；（c）前视图；（d）左视图。

图10. 含空洞波速模型的建立。（a）圈定计算区域；（b）生成网格节点；（c）获取开挖区所对应的网格节点。

4.4.2. 爆破事件定位测试

在这一小节，基于监测的信号数据，使用所提出的方法去定位记录两个钻孔爆破事件。使用AIC方法提取所记录的信号的初至到时。定位结果与误差结果展示在表3中。两个爆破事件的定位结果被分别降低了大约9 m和3 m，更接近于实际爆破位置。可以清楚地看到，由于考虑了空洞区，所提出的方法可以获得较为准确的定位结果。

4.4.3. 微震事件定位

使用本方法对2013年12月5日至2014年1月16日开挖活动中所诱发的微震事件进行定位。微震事件的空间分布如图11所示。一个微震事件的射线路径如图11所示，展示了在含空洞的模型中P波的传播路径。射线在远离空洞区域沿直线传播，而在接近空洞区域时，绕过开挖区域进行传播。相比于均一波速模型的定位结果（图9），并没有任何的微震事件被定位到空洞区域内部，而主要是分布于主厂房的下游侧边墙，以及2#和3#母线洞之间的区域。聚集区1处的微震事件集中在主厂房下游侧边墙墙趾附近，标高1680～1690 m（图11），这由开挖活动引起的应力集中所致。聚集区2处的微震事件主要分布在母线洞2#和3#之间，标高1698～1710 m，表明围岩内部存在开挖诱发裂隙。通过常规监测技术（图12）和现场喷射混凝土破裂（图13）来验证本文定位方法的定位结果的合理性。原位多点位移计的位置如图12（a）所示，位于2#母线洞上方，标高1706.5 m。其孔口绝对位移过程图表明，在2014年1月1日至2014年1月9日期间，位移呈上升趋势[图12（b）]，其间微震事件数目呈明显增加的趋势。不同区段的相对位移图[图12（c）]进一步表明，多点位移计的第24 m测点与尾端固定点之间的区段发生了明显的变形，其位置靠近微震事件的聚集区2（图11和图12）。此外，如图13所示，2#母线洞侧壁的喷射混凝土开裂和剥落进一步表明了原位岩体损伤与微震事件聚集区2之间的关系，验证了所提出的微震定位方法的可行性。

表3 使用不同的速度模型定位爆破事件的结果

5. 结论

准确的微震事件定位是微震监测技术圈定围岩损伤区的关键。现场复杂情况会对最终微震破裂源定位结果造成消极影响。在本文中，一种基于微震信号P波理论到时与实际到时之间残差的微震定位方法被提出，用于含空洞复杂区域微震破裂源定位。基于二阶差分与窄带技术，二阶快速行进法通过求解程函方程来获取P波的理论到时。在获得理论到时的基础上，微震破裂源到微震传感器的射线路径可采用线性插值和龙格-库塔方法求解获得。利用AIC方法自动提取微震信号的实际到时后，通过搜索使得目标函数值达到最小的网格节点，实现微震破裂源定位。

图11. 位于2#和3#母线洞之间的微震事件，基于含空洞速度模型的定位结果。（a）微震事件的三维空间分布；（b）俯视图；（c）前视图；（4）左视图。

图12. 多点位移计3-8的测量结果，以及日均微震事件数目。（a）多点位移计3-8的位置；（b）3-8的钻孔位移量与日均微震事件数；（c）3-8在不同分段的相对位移量。

图13. 2#母线洞边墙处喷射混凝土破裂与剥落。

本文所提出的方法通过数值实验得到验证，并应用于猴子岩水电站三大洞室的开挖。对于所记录的爆破事件的定位结果表明，与均一波速模型的定位相比，本文所提出的方法可以有效地减小定位误差。此外，通过安装多点位移计获得的现场监测结果以及2#母线洞侧壁的喷射混凝土裂缝和剥落情况，验证了本方法对开挖诱发微震事件的定位结果的合理性。该方法可用于含空洞复杂环境下的微震事件定位，可有效地帮助圈定围岩内部的损伤区域。

致谢

感谢国家自然科学基金（52039007）提供的资金支持。

Compliance with ethics guidelines

Ruochen Jiang, Feng Dai, Yi Liu, and Ang Li declare that they have no conflict of interest or financial conflicts to disclose.