复杂结构中异常区域对波速成像影响的量化研究
2021-12-30董陇军童小洁马举
董陇军,童小洁,马举 *
School of Resources and Safety Engineering, Central South University, Changsha 410083, China
1. 引言
随着地表空间资源的日益紧缺,地下空间开发受到越来越多的关注。但复杂的地质环境为地下交通运输和隧道工程建设带来了巨大的挑战[1-5],涌水、地下泥石流、塌方等地下工程灾害使人员和设备面临巨大的安全风险[6-9]。
地下工程中常使用的空间探测方法可分为两类:地震法和电磁法[10-19]。这两种方法都可以在大范围上间接预测异常结构(如富水区)的存在。其中地震法包括地质预测、断层扫描成像及陆地声纳等技术[10-15],该方法主要分析弹性波在地质体中的传播特性,并推断它们的分布、几何形态和结构特征[10-18]。电磁法,如探地雷达和瞬态电磁法,一般通过介电常数和电阻率的差异来推断地质体的特征[14]。
随着新信息技术的出现,物联网和声发射(AE)技术已经应用于材料的无损检测,主要用于动态裂纹检测和疲劳断裂监测。声发射技术可以评估组件的完整性和结构的危险等级,因此引起了人们的极大关注,该技术在航空、冶金、交通、建筑等领域得到快速发展。基于声发射信号到达时间和声发射震源位置,可以迭代求解复杂的速度结构。反演波所得到的波速场,可以更直观、更快速、更准确地检测区域异常[20-26]。
Jansen等[27]对花岗岩中的热致微裂纹进行了超声成像和声发射监测。他们的研究表明,声发射的位置和速度差异清楚地描绘了裂纹的形态。Nishizawa和Lei[28]采用扩展信息标准来推进速度层析成像研究,他们的米级实验表明该方法为断层扫描提供了一个客观的标准。在较小的范围内,Lei和Xue [29]使用差分层析成像测量了CO2注入饱和水多孔砂岩过程中的波速和衰减特性,指出由于流体扩散导致的黏性损失对多孔岩石中超声波P波的传播具有重要作用。最近,Aben等[24]在实验室尺度上研究了岩石破裂的层析成像,通过一种新的层析成像方法,量化了非断层压裂时破裂能量演化过程。
本文提出了一种基于快速匹配算法和最小二乘法的改进型三维声发射成像扫描方法,并以此检测潜在异常区域。本文通过使用合成的震源位置和到时数据,联合反演了各向异性的P波结构。通过改变个别参数,包括先验模型、传感器配置、内部事件数量、真实模型、射线覆盖率和事件定位误差,探讨了影响成像结果的不同因素。
2. 方法
在合成测试中,通过快速匹配算法和标准优化程序,采用将主动超声测量与被动声发射监测相结合的方式进行反演[30],得到三维各向异性波速成像,反演过程如图1所示。具体反演过程包含以下5个运行步骤:①确定初始环境并划分网格节点;②配置先验模型;③收集所需的声发射和超声波数据;④执行层析扫描计算并建立速度结构数据库;⑤识别层析扫描结果中的异常区域。
(1)确定初始环境。首先确定待测区域的大小和具体位置,根据待测结构的情况和反演的精度要求,确定单位立方体网格的尺寸。一般来说,网格划分得越密,反演精度越高,计算量也会成倍增加,程序处理时间越长。但当网格足够密时,继续增加网格密度,反演精度将不会有明显变化。建立与网格节点尺寸相同的零矩阵M,将矩阵索引位置(i,j,k)与网格节点位置一一对应。网格节点形成一个集合,当在后续节点间搜索最快波形路径时,它们被作为起始点。假定P波在周围非空区域的传播速度为一个未知数,用V来表示。
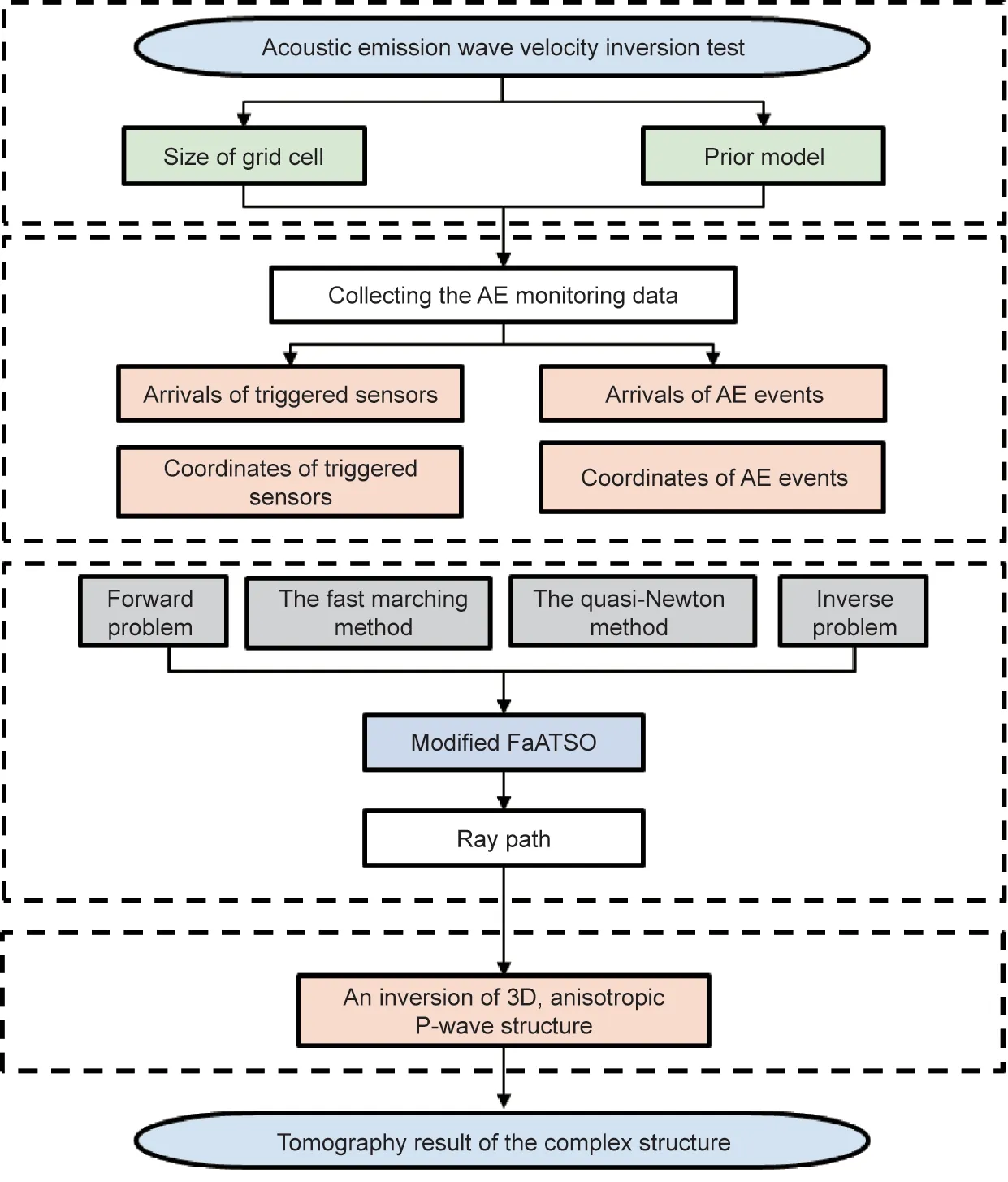
图1. 反演计算过程流程图。FaATSO:基于标准优化的声发射快速搜索成像。
(2)配置先验模型。根据待测结构特点设置先验模型,在实际应用中,待测结构内部异常区域的情况是未知的,根据待测结构有限的已知信息确定一个先验模型,代入实测数据进行迭代计算,最终得出实际反演模型,进而研究待测复杂结构内部异常区域的特征。本次合成数据实验模拟的复杂结构为中空花岗岩,异常区域为低速区,一般花岗岩波速范围为4000~5500 m·s−1,水或流体的波速一般为1500 m·s−1,所以模拟合成数据实验中真实的内部区域和外部模型的波速分别设为1500 m·s−1和4500 m·s−1,先验模型的波速为内外波速平均值。
(3)采集声发射和超声数据。在待测结构的不同位置上安装传感器。传感器同时满足主动发射脉冲和被动接收声发射信号的要求,各个传感器位置均为已知。对于三维模型,未知数有5个[P波的波速V、声发射源坐标(x0,y0,z0)、激发的初始时间t0],因而传感器数量需为大于或等于5的整数。发射脉冲信号的传感器即为主动震源Sl,位置坐标为(xl,yl,zl),发射时间为 ;接收信号的第k个传感器Sk的位置坐标为(xk,yk,zk),接收声发射P波信号的初至到时为 ;对于未知震源P0,设置其位置坐标为(x0,y0,z0),激发的初始时间为t0。
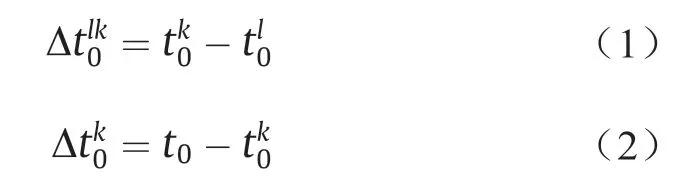
式中,表示发射脉冲信号的传感器Sl与接收脉冲信号的传感器Sk之间的实际到时差; 表示未知震源P0与接收脉冲信号的传感器Sk之间的实际到时差。
在本研究中,传感器和声发射事件的坐标(粗位置),以及信号的到达时间差,都是输入数据。
结构中每个网格点的波速通过迭代计算得到。这些值用三维图像中的不同颜色表示;动态的射线路径和声发射事件被追踪下来,因而可以通过色差直观地分离复杂结构中异常区域的边界和位置。此外,异常结构也可以根据P波速度值进行量化分区。
3. 实验
假设的100 mm×100 mm×100 mm立方体的中心有60 mm(直径)的通孔,7个传感器均匀地排列在立方体的4个垂直边上。在分析传感器布置的影响时,另外4个传感器将均匀分布在上、下表面的圆孔中。综合测试中的传感器具有主动传输脉冲功能。因此,它们不仅可以用作主动声发射源,也可作为接收器。立方体内部随机生成了600个声发射事件:异常区域内部的170个事件和其外部的430个事件。每个声发射事件的确切坐标都是已知的,并且每个事件都可以被全部传感器检测到。
下文将实际模拟的异常区域称为“内部”,其P波速度用Vin表示;外面的结构孔被称为“外部”,其P波速度由Vout表示。为了研究不同因素对速度扫描结果的影响,我们定量测试了先验模型、传感器配置、事件分布、真实模型、射线覆盖率和事件定位误差。
在计算每个节点的速度扫描结果并获得射线路径后,我们将每个网格节点的反演速度Vt与实际值Vo进行比较。如果它们之间的差异小于±20%,则速度扫描结果视为有效。为了定量表征各种影响因素对反演结果的影响,将实验中各网格的Vt与其对应的Vo来逐一对比,并确定准确率的有效范围。
4. 结果与讨论
4.1. 先验模型与传感器布置
为了评估先验模型和传感器布置对层析成像结果的影响,共进行了两组4次试验(表1)。除了围绕立方体试样放置的28个传感器之外,试验3中异常区域上方布置了4个传感器,试验4中异常区域下方也布置了4个传感器。对比试验1与试验2,以分析先验模型的影响;对比试验2、3和4,以研究传感器布置的影响。在这种情况下,移除异常区域内的170个声发射事件,而保留区域外的430个事件。
在层析成像反演之前,先获取了主动超声测量和声发射事件的到时。成像结果如图2所示。垂直于z轴的5个切平面表示三维P波速度的层析成像结果。从脉冲源到接收传感器的传播路径用蓝色曲线表示,声发射事件的射线路径用橙色曲线表示(随机选择一个声发射事件)。P波速度的定量分析如图3所示。

表1 先验模型和传感器布置表
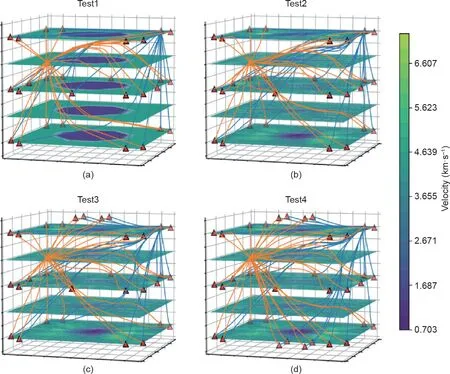
图2. 不同先验模型和不同传感器布置下的反演结果。

图3. 不同先验模型和不同传感器布置下的反演准确率(a)和速度分布范围(b)。
在图2的层析成像结果中,图2(a)呈现了一个完美的直径为60 mm的圆;图2(a)~(d)中,圆消失了。此外,在比较第二组中的三个试验时,更改传感器配置并未起到明显的作用。即使传感器布置在异常区域的表面,射线仍然绕过异常区域并穿过岩石。根据层析成像结果,在结构的上、下部分获得了相对较高的精度。这是因为布置在空区顶部和底部传感器的超声波脉冲信号穿过了内部区域。
对于第一组试验,当先验模型等于真实模型且速度精度限制在20%时,反演的Vout和Vin完全正确(图3)。对于第二组的三个试验,当先验模型与真实模型不同时,Vin的准确率小于5%(图3),这说明无法准确识别速度异常区域;但是,Vout仍然具有相对较高的准确度。
4.2. 事件分布
上一节的结果表明,当先验模型与实际情况不符时,内部P波速度是通过基于输入参数的迭代计算来获取的。然而,结果不尽如人意。外部事件的射线路径可能不会绕过内部区域,这是影响层析成像效果的原因之一。为了验证猜想是否正确,亦即内部事件是否会造成层析成像结果的差异,将170个内部事件添加到试验中。我们设置了分别对应第二组中试验2、3、4的另外三个试验。除了位于异常区域的170个声发射事件外,所有参数均保持不变(表2)。
试验结果如图4和图5所示。与异常区域表面上的传感器不同,来自内部事件的射线必须穿过异常区域。然而,试验结果与之前的一致。这表明当真实模型Vout/Vin等于4.5/1.5时,内部事件的添加并没有有效改善层析成像的结果。
上述实验得到的层析成像效应表明,当外部和内部(异常)区域的实际P波速度分别为4.5 km·s−1和1.5 km·s−1,先验模型输入的Vout=Vin= 3 km·s−1时,异常区域的反演精度低于5%。改变传感器布置或增加异常区域的声发射事件数对反演结果几乎没有影响。
4.3. 真实模型
我们进一步分析了真实模型和先验模型对层析成像结果的影响。在新的试验中,真实模型中的Vout/Vin从4.5/1.5变化到4.5/4.0。先验模型使用Vout和Vin的平均值。异常区域没有采集到声发射事件。实验配置列于表3。
层析成像结果(图6)和准确率(图7)表明,当Vout和Vin之间的差值较小时(即Vout/Vin更接近1),反演结果更好。特别地,试验5和试验6中Vout和Vin的准确度几乎达到了。图6还显示了试验5和试验6的射线路径不太弯曲或接近直线状。
我们将速度精度容差从20%缩小到15%,最后缩小到1%。如图8所示,在试验5和试验6中,当精度容差分别限制在5%和1%时,Vout和Vin的准确率超过了50%。当Vout/Vin为4.5/4.0或4.5/3.5时, 即(Vout−Vin)/Vout小于25%,尽管只布置了28个传感器且没有内部事件,此时的反演结果依然非常好。

表2 异常区域内部事件对反演结果影响试验测试方案
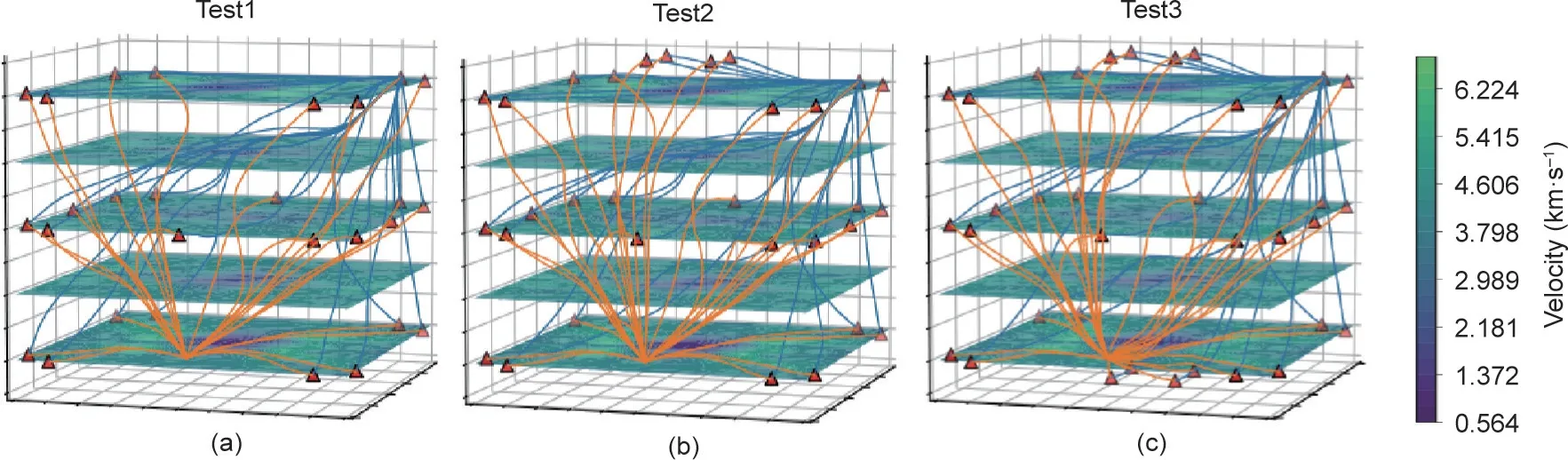
图4. 在异常区域分布内部事件时不同传感器布置方式下的反演结果。(a)使用28个环绕传感器;(b)使用28个环绕传感器及4个顶部传感器;(c)使用28个环绕传感器、4个顶部传感器及4个底部传感器。
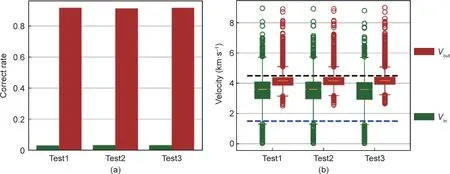
图5. 在有内部事件时不同传感器布置下的反演准确率(a)和速度分布范围(b)。

表3 真实模型和先验模型对反演结果影响试验测试方案
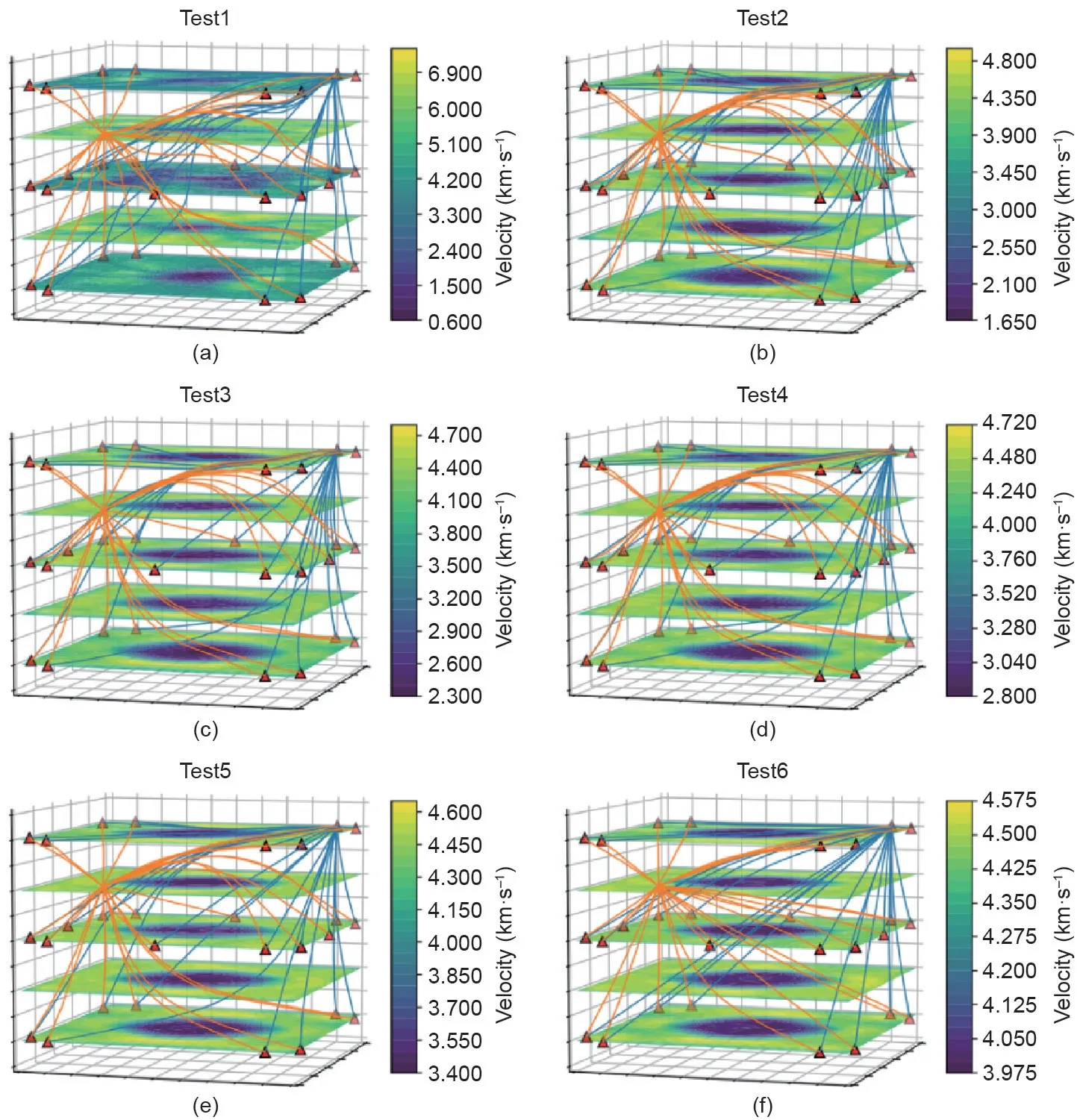
图6. 不同真实模型和先验模型下的反演结果。(a)真实模型中的Vout为4.5 km·s−1,Vin为1.5 km·s−1,先验模型对应的波速均为3.0 km·s−1;(b)真实模型中的Vout为4.5 km·s−1,Vin为2.0 km·s−1,先验模型对应的波速均为3.25 km·s−1;(c)真实模型中的Vout为4.5 km·s−1,Vin为2.5 km·s−1,先验模型对应的波速均为3.5 km·s−1;(d)真实模型中的Vout为4.5 km·s−1,Vin为3.0 km·s−1,先验模型对应的波速均为3.75 km·s−1;(e)真实模型中的Vout为4.5 km·s−1,Vin为3.5 km·s−1,先验模型对应的波速均为4.0 km·s−1;(f)真实模型中的Vout为4.5 km·s−1,Vin为4.0 km·s−1,先验模型对应的波速均为4.25 km·s−1;
随着Vout和Vin之间的差值逐渐增大,Vin的反演精度下降。然而,如试验2、3和4的路径图所示,仍然可以区分Vin(异常)区域(图6)。当Vout和Vin分别为4.5 km·s−1和1.5 km·s−1,射线路径曲折且无法检测到内部区域。
由于准确率随着Vout和Vin之间的差异而变化,我们将指数E定义为:
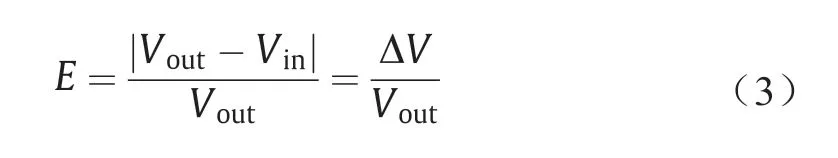
上述合成试验中不同E值对应的反演结果如表4所示。
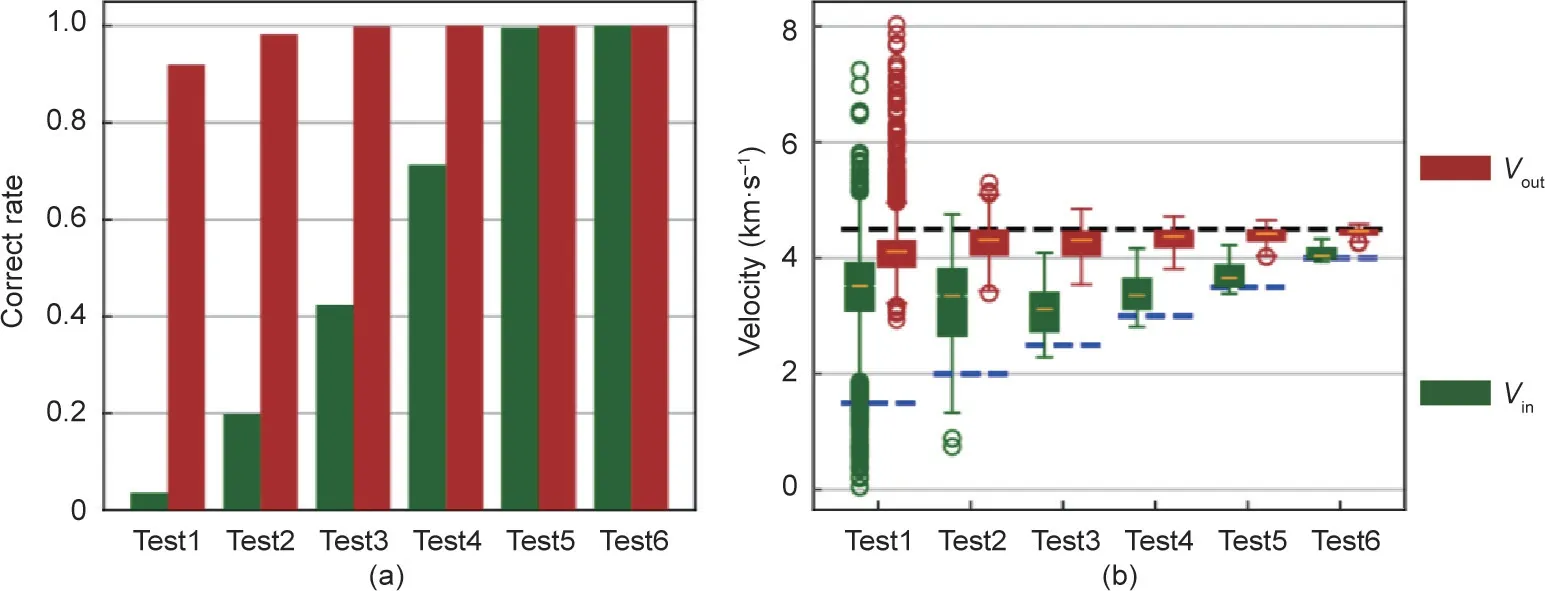
图7. 不同真实模型和先验模型下的反演准确率(偏差20%视为正确)(a)和速度分布范围(b)。
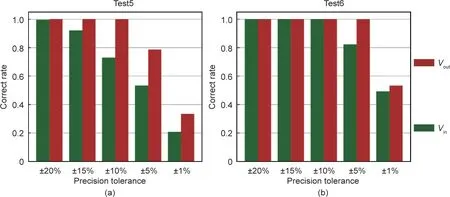
图8. 在不同精度容差下,试验5和试验6中真实模型和先验模型的定量影响。

表4 不同E值下反演效果统计表
在先验模型、真实模型、传感器配置和内部事件4个影响因素中,真实模型对层析成像结果起着决定性作用。当真实模型中的Vout/Vin为4.5/1.5时,层析成像结果误差较大;传感器配置的变化和内部事件的增加并没有改进层析成像结果。当指标E高于50%时,结果不可靠;当E在25%到50%之间时,结果可靠稳定;当E小于25%时,结果具有较高的准确度。此外,虽然层析成像结果总体较差,但上下部分的Vin以及Vout的准确度相对较高。
4.4. 射线覆盖
当内外P波速度差值过大时,所用的方法都未能改进结果。P波的射线路径在不同介质中会发生变化。介质差异越大,传播机制越复杂,反演精度越低,这是当前声发射波速层析反演方法普遍存在的局限性[30]。
在复杂结构中进行了6项额外的试验(表5)。异常区域内未产生声发射事件,异常区域外声发射事件从0增加到400。反演的P波速度与实际值之间的精度容差限制在±5%。结果如图9和图10所示。
从试验1到试验6,内部异常区域的识别精度随着外部声发射事件的增加而增加(图9)。此外,Vin的精度随着声发射事件而增加,而Vout精度保持相对较高(图10)。
上述分析表明,真实模型在具有较高的反演精度范围时,提高射线覆盖率(通过增加外部声发射事件数)
可以提高反演精度。然而,随着声发射事件数的增加,反演精度的增长率趋于平缓(图10),这意味着无法通过无限增加声发射事件数而显著提高准确率。因此,在实际应用中,需要确定合适的声发射事件数或范围,以便在相对较少的声发射事件数下获得更高的精度,从而节省计算成本。

表5 射线覆盖范围对反演结果影响试验测试方案
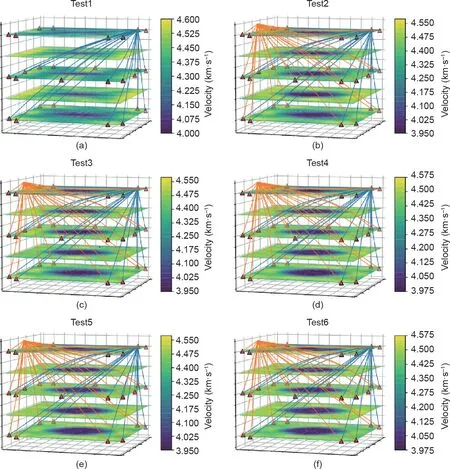
图9. 不同射线覆盖率下的反演结果。(a)仅使用主动超声脉冲射线;(b)使用主动超声脉冲射线及50个声发射事件的射线;(c)使用主动超声脉冲射线及100个声发射事件的射线;(d)使用主动超声脉冲射线及200个声发射事件的射线;(e)使用主动超声脉冲射线及300个声发射事件的射线;(f)使用主动超声脉冲射线及400个声发射事件的射线。

图10. 不同射线覆盖率下的反演准确率(容差5%视为正确)(a)和速度分布范围(b)。
4.5. 事件定位误差
在合成试验中,事件是自动生成的,因此可以精确地知道它们的位置。然而,在实际应用中,声发射事件的位置是未知的。目前,有多种声发射定位方法大大减小了定位误差[4,7-9],如无需预先测量波速的方法 [7]。尽管如此,定位结果与实际位置之间仍然存在差距,因此,需要研究定位误差对反演结果的影响。
我们研究了两种方案。在第一种方案中,所有声发射事件都有误差,允许的位置变化范围从(0.95, 1.05)扩大到(0.75, 1.25),即定位误差从±5%增加至±25%,间隔为5%。在第二种方案中,定位误差固定在±20%,误定位事件由50次增加到300次,间隔为50次;其他条件与方案1相同。方案1和方案2的配置分别列于表6和表7。结果如图11至图14所示。
方案1的反演结果如图11所示。从试验1到试验6,误差范围从±5%增加至±25%,层析成像效果逐渐变差。对于试验3,错误范围在±10%时,中心异常区域仍能观察到柱状结构。当误差范围达到±15%或以上时(即试验4、5、6),根据反演结果图,内外波速边界模糊,难以观察到该结构中的异常区域。
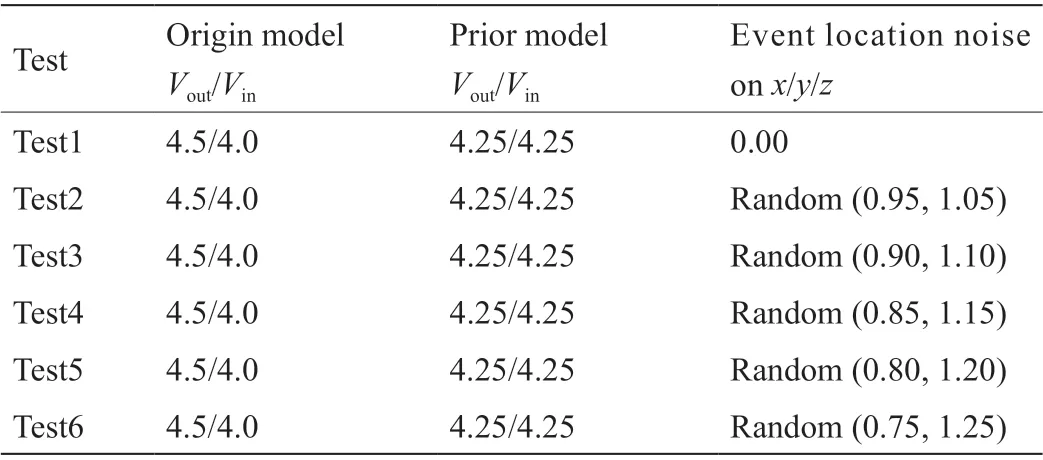
表6 不同定位误差对反演结果影响测试方案
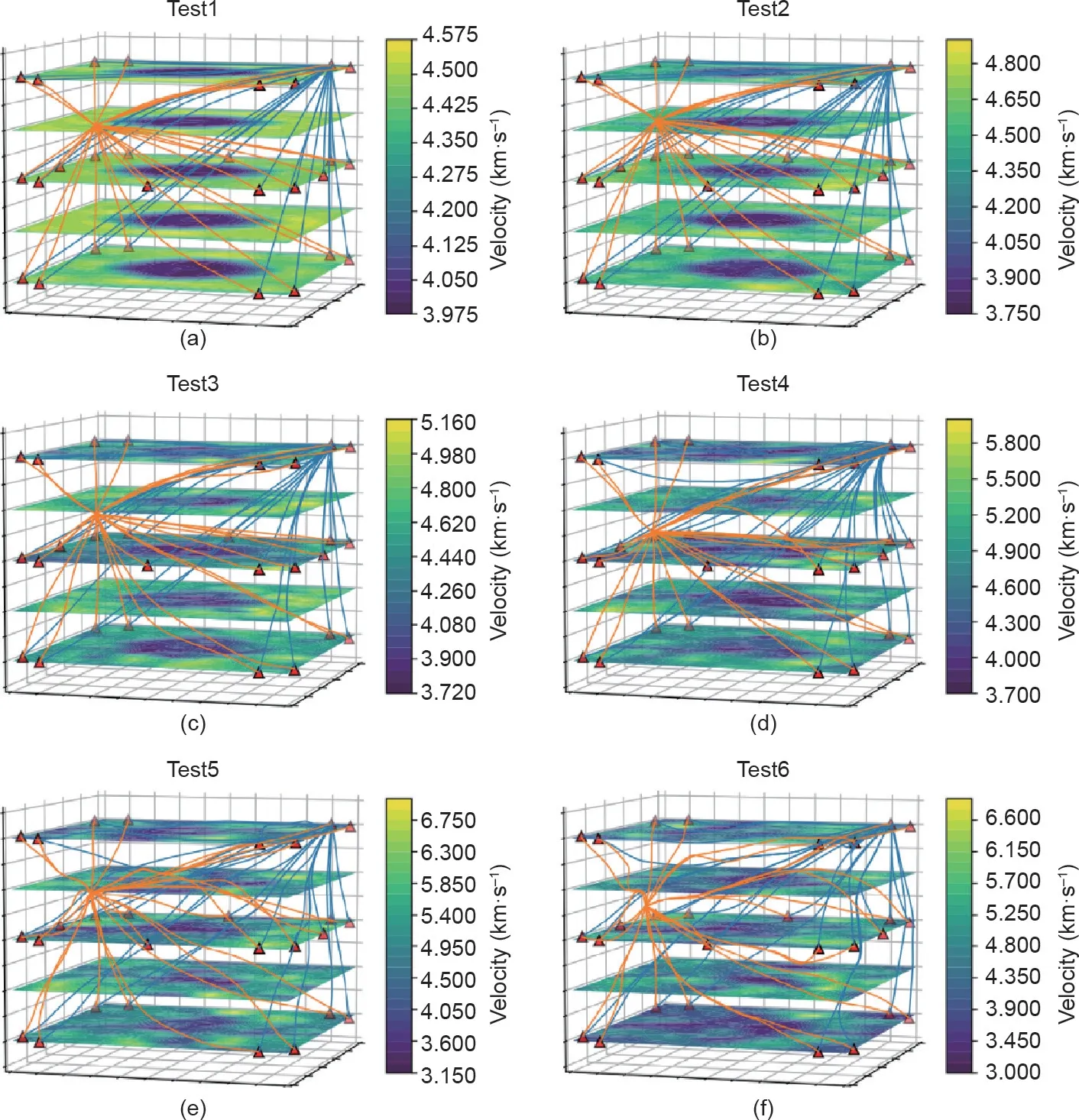
图11. 不同定位误差下的反演结果。(a)事件坐标无任何误差;(b)事件的真实坐标值按0.95~1.05倍随机调整;(c)事件的真实坐标值按0.90~1.10倍随机调整;(d)事件的真实坐标值按0.85~1.15倍随机调整;(e)事件的真实坐标值按0.80~1.20倍随机调整;(f)事件的真实坐标值按0.75~1.25倍随机调整。

表7 不同误定位事件数量对反演结果影响测试方案

图12. 不同定位误差下的反演准确率(a)和速度分布范围(b)。
方案1(图12)的量化结果表明,当定位误差为±10%时,准确率超过70%。在实际应用中,声发射试验的定位误差很容易控制在10%以内[7];对于边长为100 mm的试样,定位误差可以小于10 mm。因此,声发射波速层析成像方法在Vout/Vin为4.5/4.0、定位误差合理的情况下,能可靠地反演出复杂结构中异常区域的大小和范围。
方案2反演结果如图13所示,随着误差事件数从50个增加到300个,反演效果逐渐变差。定量分析图(图14)显示从试验1到试验6准确率不断下降,下降幅度比方案1慢。
与4.3节的试验6比较表明,错误的定位数据对反演结果有很大影响。当准确率允许误差为5%时,定位准确的声发射事件数由430个变为350个;定位错误50个时,Vout和Vin的准确率分别由100%下降到95%和由83%下降到75%。当声发射事件定位错误数增加到300个(总共400个事件)时,Vout和Vin的准确度降低到30%左右;反演结果不再可靠。因此,不合理、误定位的声发射事件影响层析反演的精度。我们注意到在这个合成试验中,Vout总是比Vin更准确。由于异常区域的波速较低,射线会绕过该区域的边界。由于通过的射线很少,因此缺少射线数据来计算Vin,最终导致Vin的计算结果不太准确。
5. 结论
为了分析声发射波速层析成像反演的影响因素,采用了一种改进的主动与被动声发射源相结合的三维层析成像方法,进行了多种比较综合试验,定量分析评价了先验模型、传感器配置、内部事件、真实模型、射线覆盖率和事件定位误差6个因素的影响。结果表明,优化输入参数可以显著提高复杂结构异常区域的层析成像可靠性。
在这6个影响因素中,真实模型对层析成像结果起着决定性的作用。因此,当异常区域与其周围区域的P波速度相差较大时,很难取得理想的效果。内外波速之差用指数E表示,当E≥ 50%时,反演结果不可靠。在未来的研究中,我们将考虑当E值太高时向低速区域增加权重,以减小E值,进而恢复对正确波速值的反演结果。
当E在合理的范围时,可以获取一个具有较高层析成像精度的结果。当外部声发射事件数减少时,反演精度降低;随着事件数的增加,准确率的提高速度变缓。因此,应确定与较高准确率相对应的事件数,为实际应用提供最佳方案。定位误差的增大也会影响反演精度。通过对声发射事件进行筛选,剔除不合理的声发射事件,可以提高层析反演效果。
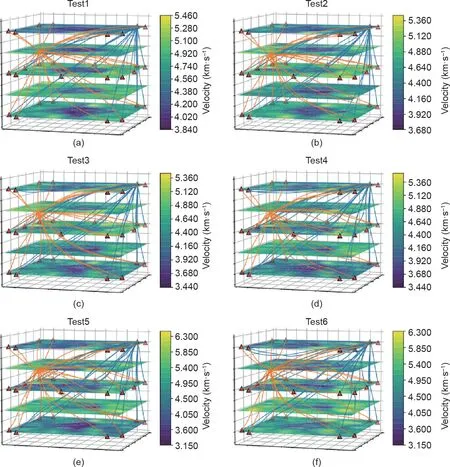
图13. 不同误定位事件数量下的反演结果。(a)全部事件中有50个事件存在定位误差;(b)全部事件中有100个事件存在定位误差;(c)全部事件中有150个事件存在定位误差;(d)全部事件中有200个事件存在定位误差;(e)全部事件中有250个事件存在定位误差;(f)全部事件中有300个事件存在定位误差。
这种速度成像方法的前提是材料必须横向各向同性(VTI),在实践中,VTI几何形状的假设特别适用于实验室中承受三轴压缩的岩石试样。这种方法不太适用于结构内波速有较大差异的情况。对于波速变化缓慢的情形,该方法更为可靠和稳定。在这项研究中,我们只测试了一个圆柱形的异常区域,实际情况要复杂得多,在形状异常的情况下,层析成像的精度可能会有所不同。由于先验模型对反演非常重要,因此建议在岩石试验中采用两步法,即首先进行超声测量以估计结构中的近似波速,然后将其用作后续声发射层析成像的先验模型。
致谢
感谢国家自然科学基金项目(51822407、51774327、51904334)的支持。
Compliance with ethics guidelines
Longjun Dong, Xiaojie Tong, and Ju Ma declare that they have no conflict of interest or financial conflicts to disclose.
