基于响应面法的聚丙烯高强土工格室拉伸性能
2021-12-30张冰冰阿肯江托呼提
张冰冰,刘 杰,,阿肯江·托呼提,王 斌,陈 石
(1.新疆大学 建筑工程学院,新疆 乌鲁木齐 830047;2.新疆维吾尔自治区交通规划勘察设计研究院,新疆 乌鲁木齐 830006;3.兰州德科工程材料有限公司,甘肃 兰州 730030)
土工格室是一种由高密度聚乙烯(HDPE)或聚丙烯(PP)经超声波焊接或注塑连接制作而成的网状立体土工合成材料,具有强度高、耐久性强等优点,在土体加固方面,相比平面加筋材料,具有非常强的优势[1-4].
目前,对土工格室力学性能的研究大多停留在单根条带或单个节点方面.在土工格室强度设计取值方面,欧盟设计标准通过考虑展开土工格室后1 m宽度范围内有效节点的4种破坏模式(拉伸、剪切、剥离、局部应力集中)中土工格室强度的最小值乘以节点数量作为土工格室的强度指标.中国设计标准中无土工格室整体强度指标的确定方法,工程实践中通常将条带强度换算为单位宽度作为土工格室的强度指标,忽略了土工格室条带强度与整体强度之间的匹配关系[5-7].Parsons等[8]指出土工合成材料的拉伸应力-应变关系具有应变率相关性,并且拉伸速度影响着应变率.Shadmand等[9]发现土工合成材料在拉伸过程中的应力-应变关系曲线呈非线性关系,并且后期出现了明显塑性特征.李俊伟等[10]通过HDPE土工格室片材拉伸试验,发现拉伸速率与格室片材的应力、应变率呈线性相关特性.顾良军等[11]通过土工格室结构层拉伸试验,发现土工格室的破坏发生在受力端附近的焊点处,因此认为应将格室节点强度作为格室抗拉强度设计标准值.韩晓等[12]研究了单层土工格室埋深、焊距以及地基土压实度对地基承载力和变形特征的影响,发现土工格室焊距对加固以后的地基承载力有明显的影响.综观上述,对于土工格室整体强度与条带、节点强度之间的匹配关系研究还较少,导致工程设计时无法正确确定每延米土工格室的整体抗拉强度,影响了土工格室的推广应用.
本文对不同高度、焊距的土工格室开展不同加载速度下的双轴拉伸试验研究,分析不同工况下土工格室抗拉承载力与变形之间的响应关系,并采用响应面法分析加载速度、土工格室高度、焊距对土工格室整体抗拉承载力和变形规律的影响,以期为土工格室设计参数的取值提供理论依据.
1 材料与方案
1.1 试验材料
土工格室条带为聚丙烯树脂(PP)材质,宽度分别为50、75、100 mm,断裂拉力分别为10、18、21 k N,断裂延伸率分别为17%、22%、26%.
土工格室结点采用插接式节点+整体注塑工艺,条带材料无破损,结点连接状态良好.为了便于分析,选取相同材质、厚度的条带,按照不同焊距、高度,统一加工成8个节点的网格形式,如图1所示.
图1 土工格室示意图Fig.1 Schematic diagram of geocell
1.2 测试仪器
试验采用GST 2100型静载双轴拉伸试验系统,伺服电机双轴加载,最大拉力为300 k N.试验时可以将拉力荷载均匀传递到每个节点上,并在加载装置和夹持装置之间设置力值传感器,用于测量试验过程中的拉力荷载,以达到测量数据准确真实.在土工格室节点和片材上粘贴标记反光贴,采用粒子图像测速系统(100 fps)通过高速摄影来分析标记点间距离,得到拉伸过程中土工格室条带的实时变形.
1.3 试验方案
采用控制变量法分析双轴拉伸机的加载速度、土工格室高度和土工格室焊距等3个因素对土工格室拉伸抗拉性能的影响.试验共设置28种工况,如表1所示.

表1 试验工况Table 1 Test conditions
1.4 试验过程
试验过程主要包括土工格室安装、粘贴标记反光贴、高清拍摄相机的调试,以及土工格室的双轴拉伸.试验前,先将土工格室用夹具将土工格室固定在双轴拉伸试验机上,启动双轴拉伸试验机将土工格室拉紧,确保土工格室网孔大小相同,相邻条带互相垂直.
土工格室条带是一种塑性材料,常规测试方法不能准确地得出土工格室条带在X轴、Y轴方向上的变形.本文采用粒子图像测速法(PIV法)来测试土工格室在X轴、Y轴方向的位移.在土工格室表面粘贴标记反光贴,作为PIV法测应变量的参考粒子,如图2所示.在PIV法测试系统和静载双轴拉伸试验系统之间用同步转换器连接,可以保证2个系统同步测出同一时刻条带的变形和土工格室在X轴、Y轴方向的拉力和变形量.

图2 土工格室粘贴反光粒子图Fig.2 Geocell paste reflective particle map
2 结果与分析
土工格室双轴拉伸试验中X轴、Y轴采用相同的拉伸速度,X轴、Y轴的拉力-位移关系基本一致,本文选取X轴试验数据作为研究对象.
2.1 格室焊距对整体拉力的影响
土工格室焊距影响着加筋结构的极限承载力和变形.因此,确定合适的土工格室焊距,可以保证在满足加筋结构承载力的同时,节省材料.土工格室在5 mm/min加载速度下,高度为75 mm时的断裂拉力值如表2所示.由表2可见:土工格室焊距为350 mm时的断裂拉力比400 mm时提高了21.6%,400 mm时的断裂拉力比450 mm时提高了6.9%,说明土工格室断裂拉力的提高与焊距并非反相关关系;当焊距增大到一定程度以后,土工格室断裂拉力的提高并不明显.
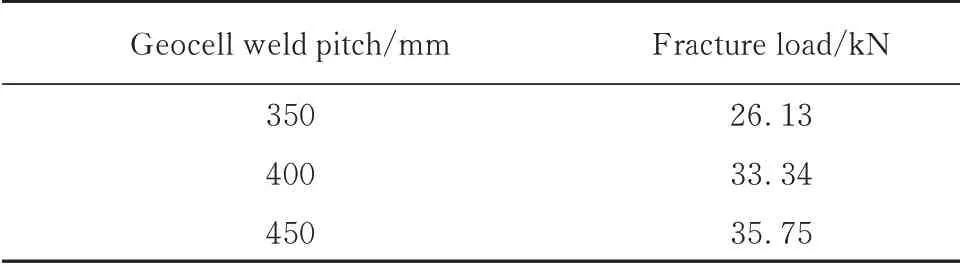
表2 不同焊距土工格室的断裂拉力值Table 2 Fracture tension value of geocell with different weld pitches
图3为不同焊距格室的拉力-位移曲线.由图3可见:(1)随着拉伸位移的增加,拉力整体呈现近似线性增长.在位移变化量为10~20 mm内,拉力值有小幅突变,出现了第1次拉力值-位移突变台阶,这是由于拉伸过程中土工格室条带牵拉夹具,夹具位置调整引起应力松弛,从而造成了拉力突变.在位移变化量为40~50 mm时,拉力-位移曲线出现了第2次小幅的突变台阶,此时是土工格室节点注塑体的破坏引起的拉力值突变.之后土工格室拉力-位移曲线继续线性增加,此时节点处插焊钢芯承担全部拉力.(2)工况13、14、15出现第2次突变台阶时,土工格室的整体拉力分别占极限破坏拉力的80%、71%、66%,位移量分别占极限位移量的86%、76%、73%,对应的土工格室条带拉力分别为1.79、1.72、1.82 k N,分别占土工格室条带断裂拉力的9.9%、9.7%、9.5%,断裂变形量的8.5%、8.2%、8.6%.因此,在工程设计中从节点承载力与条带承载力匹配的角度考虑,可以选取条带断裂承载力的10%、极限承载力的70%和位移变量的75%,作为土工格室的极限破坏荷载和极限变形.
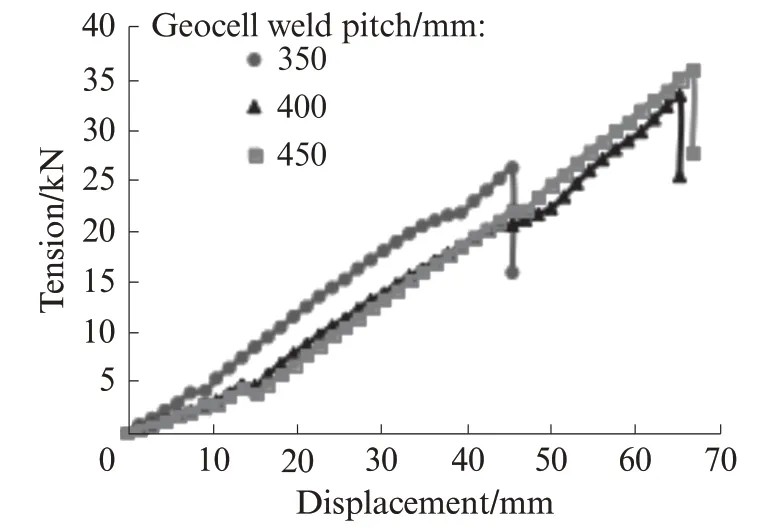
图3 不同焊距土工格室的拉力-位移曲线Fig.3 Tension-displacement curves of geocell with different weld pitches
2.2 格室高度对整体拉力的影响
在相同加载速度(5 mm/min),相同的焊距(400 mm),不同格室高度的条件下,土工格室双轴拉伸试验的整体拉力如图4所示.位移变量在50~70 mm之间时,不同高度的土工格室先后出现了节点断裂破坏,如图5所示,其断裂承载力如表3所示.由图4、5和表3可见:(1)工况14的极限承载力比工况11提高了25.2%,工况17的极限承载力比工况14提高了22.9%,土工格室高度与极限破坏拉力值呈正线性相关关系.在不同土工格室高度的条件下,拉力值随着土工格室高度的增大而增大,并对土工格室的拉力影响较大.(2)随着位移量的增加,工况11的拉力逐渐呈现线性增加,在位移为55 mm左右时达到峰值,此时节点达到极限承载力,发生破坏.工况14、17土工格室节点发生破坏时的整体位移为65 mm.(3)达到极限承载力后,拉力-位移曲线立即垂直下降,说明该材料达到极限承载力时发生脆性破坏.
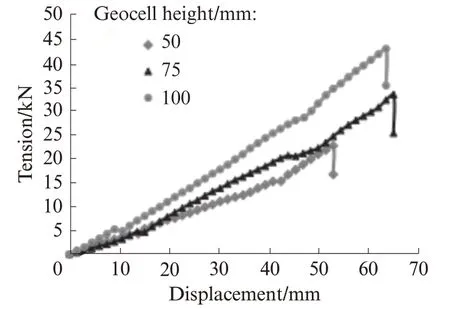
图4 不同高度格室的拉力-位移曲线Fig.4 Tension-displacement curves of geocell

图5 土工格室节点断裂破坏图Fig.5 Fracture failure diagram of geocell node
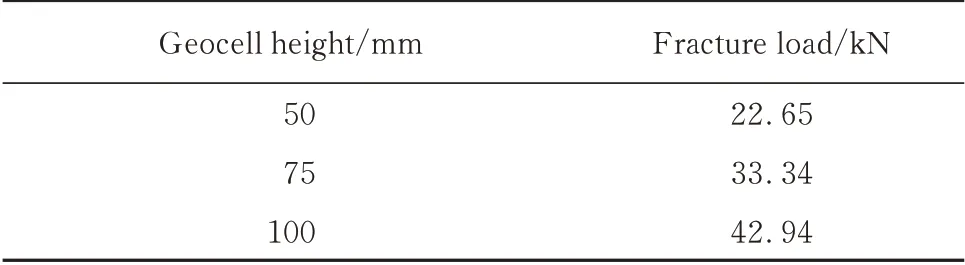
表3 不同高度格室的断裂拉力值Table 3 Fracture tension value of geocell with different height
2.3 加载速度对整体拉力的影响
通过利用等差抽样法在相同土工格室高度(75 mm)、相同土工格室焊距(400 mm),不同加载速度的20组试验数据中等差抽取4组试验数据,如表4所示.

表4 土工格不同加载速度下的断裂拉力值Table 4 Fracture tension values of geocell at different loading velocity
图6为加载速度与土工格室断裂拉力的拟合曲线.由图6可知,土工格室拉力与加载速度呈现二次项递增的关系,拉力随着加载速度的增大逐渐增大[13].相关系数R2=0.998 9,加载速度对土工格室拉力的影响显著.
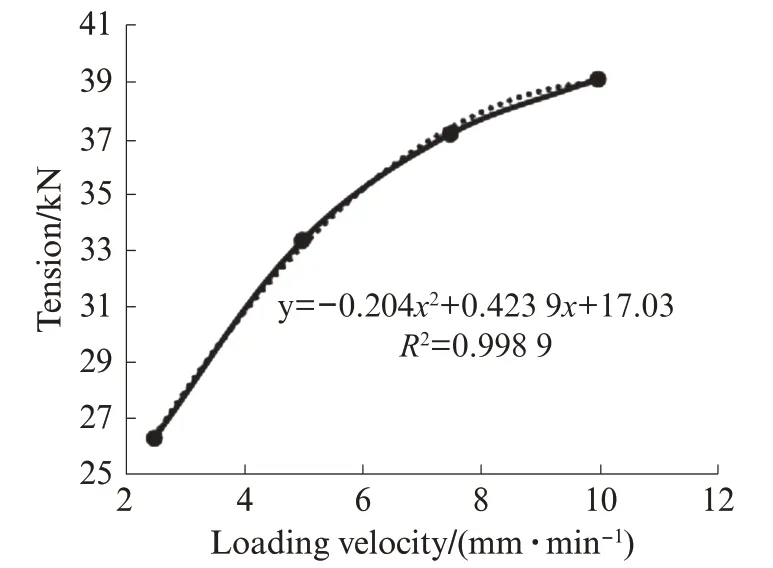
图6 土工格室拉伸试验的加载速度-拉力曲线Fig.6 Loading velocity-tension curve of tensile test of geocell
3 响应面优化分析
响应面法是在科学研究中经常用到的一种试验条件优化方法[14].响应面法类似于正交试验法,适用于解决非线性数据处理的相关问题,可以连续地对试验的各个水平进行分析,得出更加合理、可靠的结果.采用响应面多因素试验分析方法进行土工格室双轴拉伸受力和变形变化规律分析,试验因素编码如表5所示.其中,因素X1为加载速度,X2为土工格室高度,X3为土工格室焊距.

表5 试验因素编码Table 5 Coding of test factors
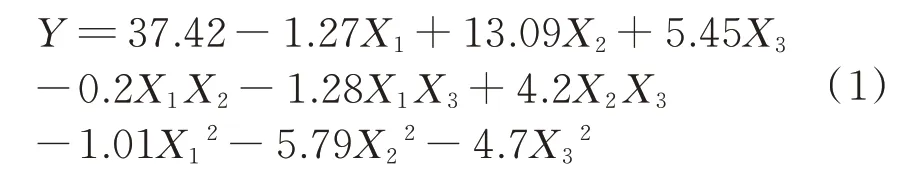
3.1 响应面试验结果与分析
通过利用Design-Expert 8.0软件的Box-Behnken模块对试验数据进行处理,如表6所示.对所得结果二次模拟拟合,建立二次多元回归方程,其土工格室双轴拉伸试验整体拉力Y的计算方程式为:
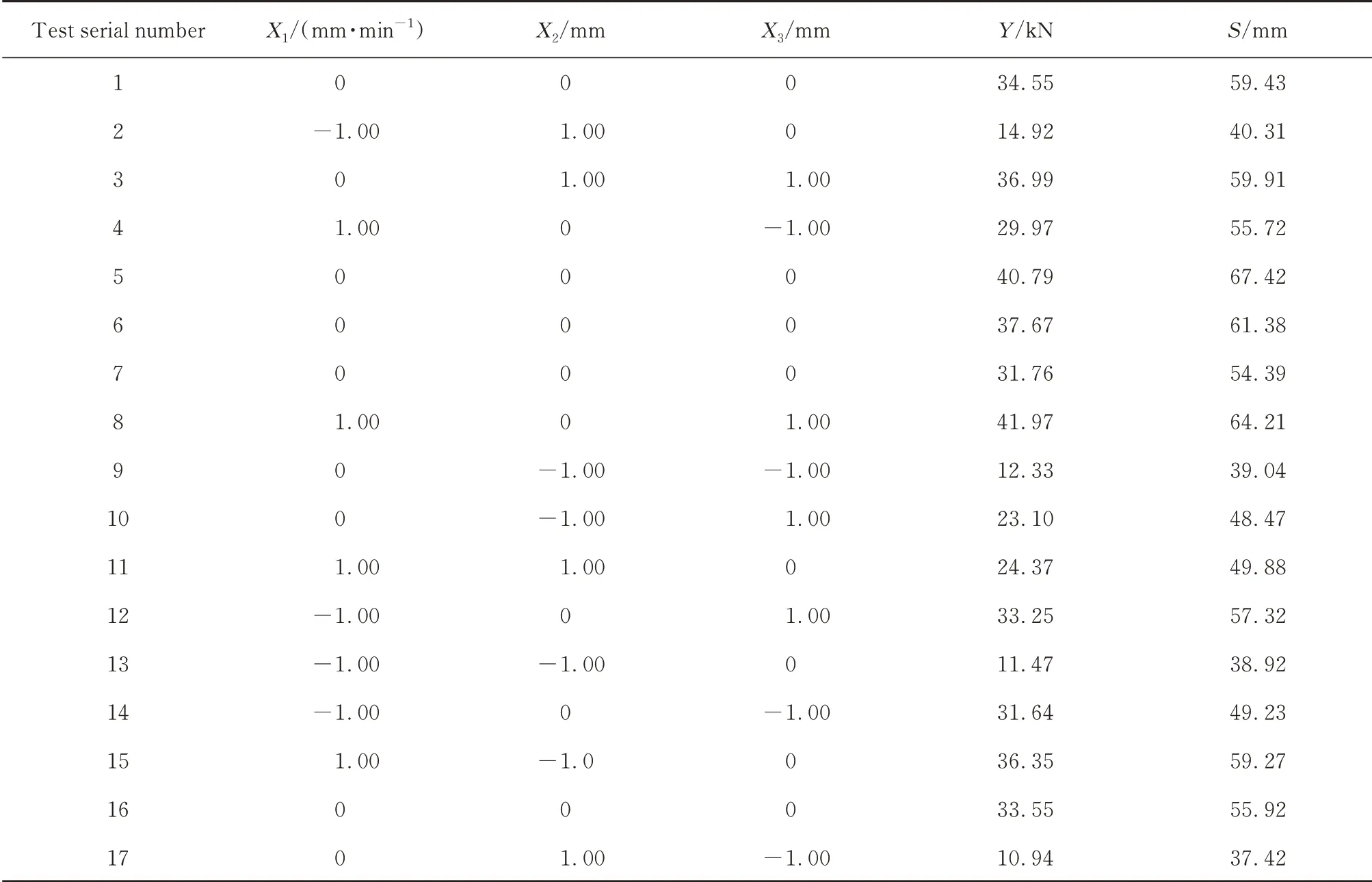
表6 试验处理结果Table 6 Experimental treatment results
土工格室拉伸整体变形位移S的计算方程式为:

其中通过优化后的模型系数Ry2=0.964 7,Rs2=0.966 5.可以看出该数据模型的相关性特别显著,并且在本试验中模型显著性检验P值都远小于0.05,可知该数据模型具有统计学意义[15],因此该模型可用于土工格室双轴拉伸试验整体拉力和土工格室拉伸整体变形位移预测和分析.
通过对土工格室整体拉力及变形位移数据方差分析,如表7、8所示,采用失拟项来表示所用模型和试验拟合的程度即表示二者的差异程度.方差分析结果的P值都大于0.05,可知对模型是有利的,没有失拟因素的存在,由此可以用该回归方程代替试验真实点对试验结果进行分析.通过F值可以分析得出,影响土工格室双轴拉伸试验整体拉力和土工格室拉伸整体变形位移的主次因素(由高到低):土工格室高度>土工格室焊距>加载速度.
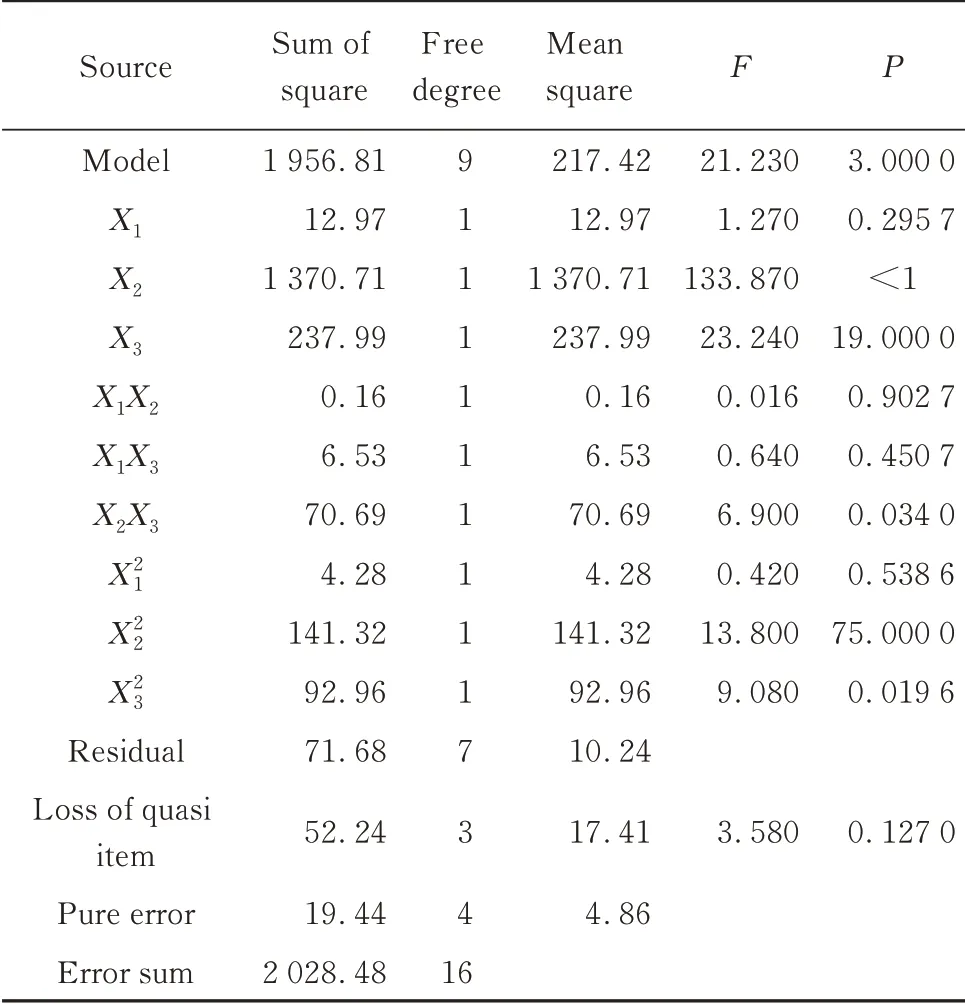
表7 双轴拉伸试验整体拉力的方差分析Table 7 Variance analysis of the overall tension in biaxial tensile test
3.2 各因素之间的交互作用
响应面曲线图表示的是响应值与其中2个因素构成的三维图,可以通过响应曲面的弯曲程度来判断各因素间的相互影响程度,弯曲度越陡说明各因素之间的交互作用越显著,反之曲面的弯曲度越缓说明交互作用显著性越小[16].为分析土工格室高度、土工格室焊距及加载速度之间的交互作用对土工格室双轴拉伸试验整体拉力和土工格室拉伸抗拉变形位移的影响,绘制各个因素之间交互作用影响的响应曲面.
土工格室焊距和加载速度对土工格室整体拉力的交互作用影响如图7所示.由图7可见:响应面图及等高线图可得整体拉力随着格室焊距和加载速度的增加呈现非线性的抛物线趋势的变化,并且通过响应面图得出在土工格室焊距400 mm左右,加载速度5 mm/min时,土工格室整体拉力达到最大值,接近40 k N.
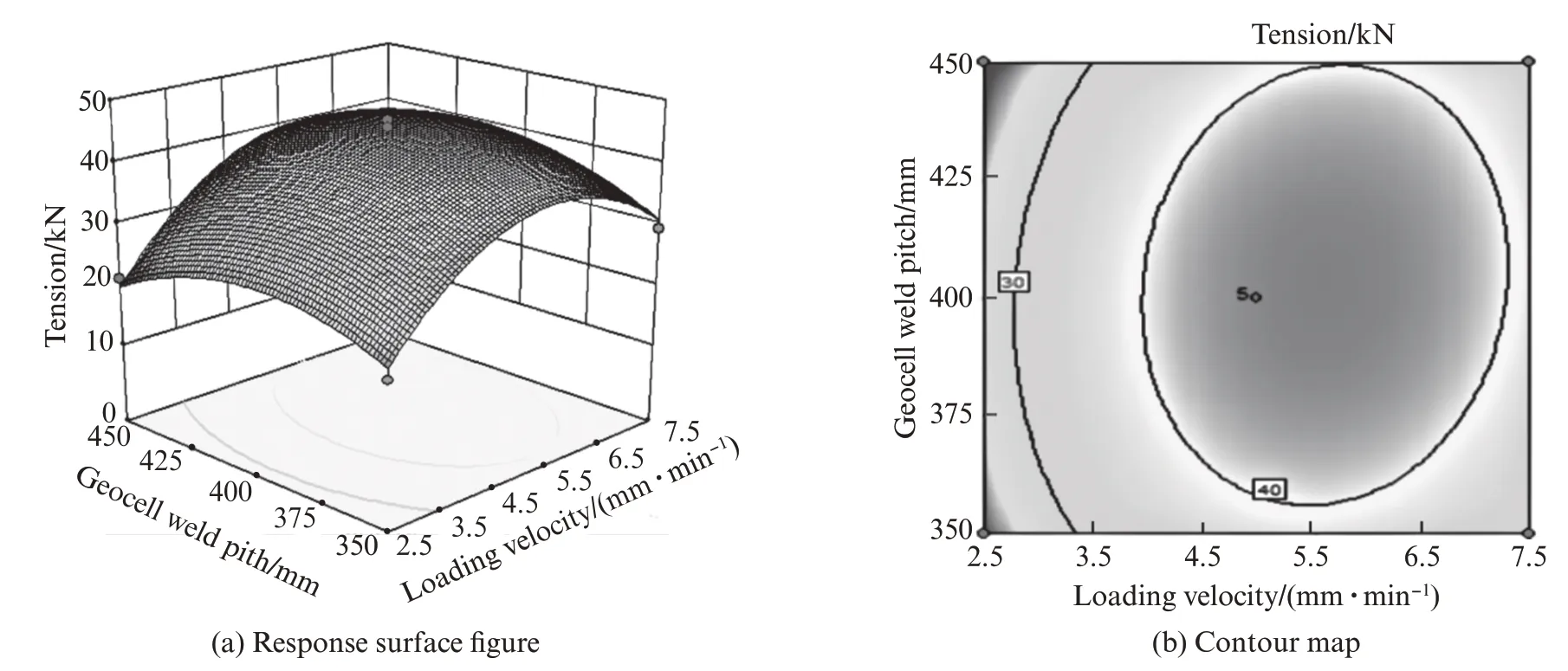
图7 格室焊距和加载速度对整体拉力的影响Fig.7 Influence of geocell weld pitch and loading velocity on test tension
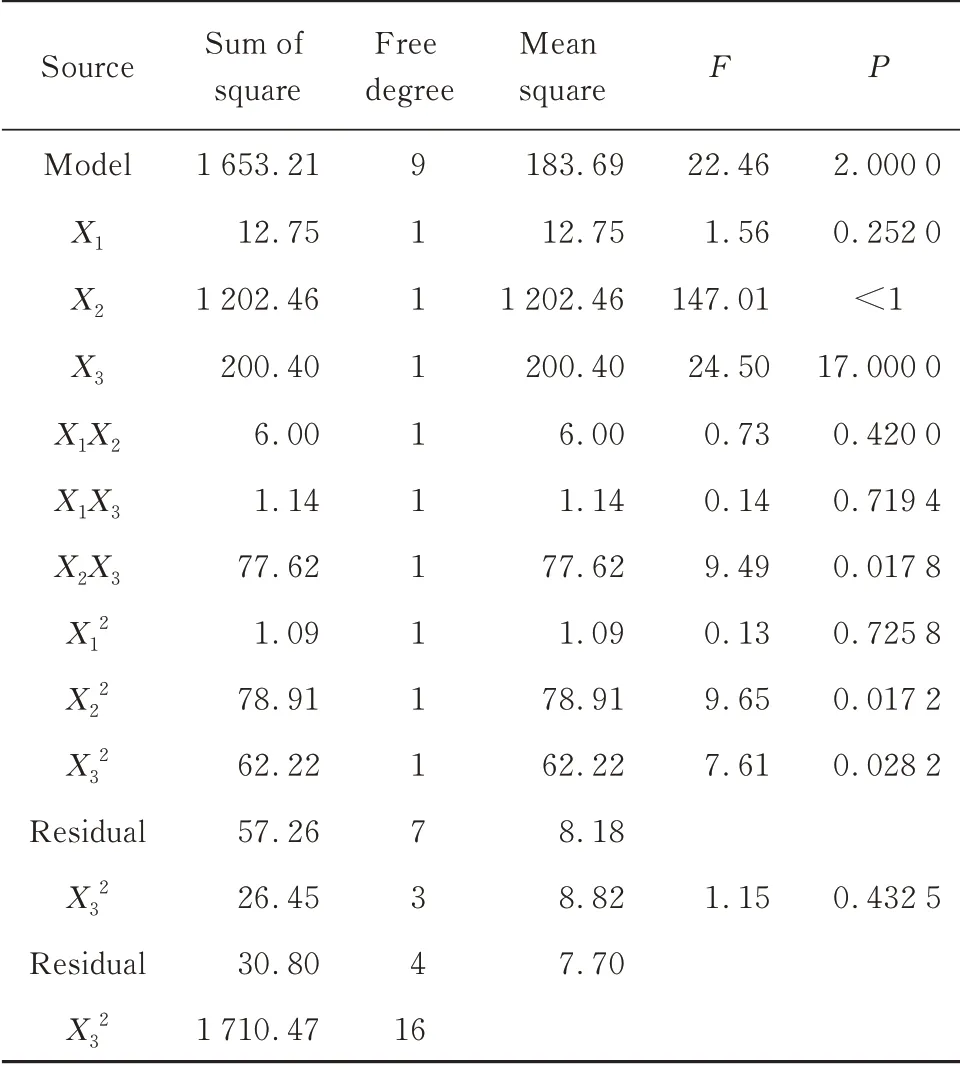
表8 土工格室拉伸整体变形位移的方差分析Table 8 Variance analysis of deformation and displacement of geocells in tension
图8为土工格室高度和加载速度对土工格室整体拉力的影响.由图8可见:土工格室高度和加载速度对土工格室整体拉力的影响较为显著,土工格室整体拉力值随着土工格室高度的增加逐渐有明显的增加趋势,对提高土工格室的抗拉承载力效果显著;土工格室整体拉力随着加载速度显著变化影响较小,在加载速度为4.5~6.5 mm/min时达到最佳值.
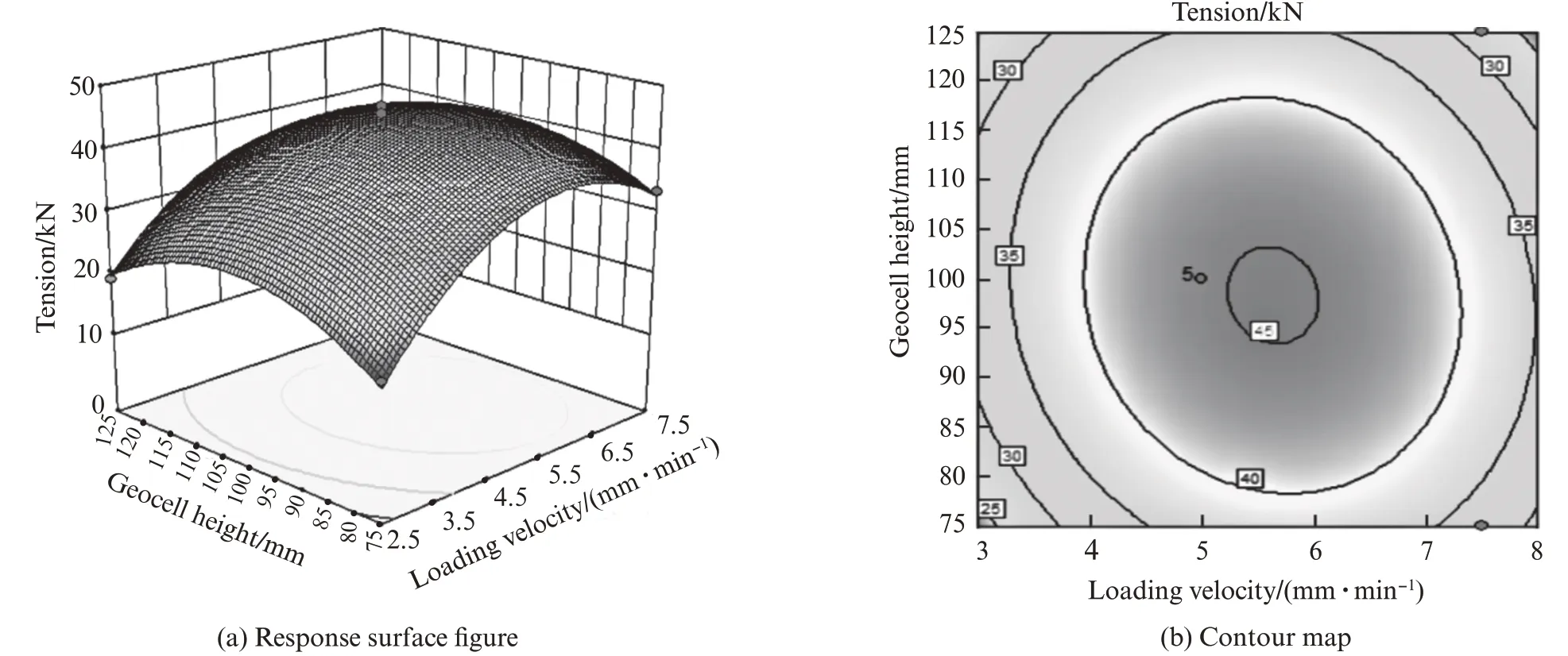
图8 格室高度和加载速度对整体拉力的影响Fig.8 Influence of geocell height and loading velocity on test tension
图9为土工格室焊距和高度对土工格室整体拉力的影响.由图9可见:土工格室焊距和高度交互作用显著性小,并且随着土工格室焊距和高度的增加,土工格室整体拉力的变化较小,在33~40 kN之间;在土工格室高度为75 mm、焊距为400 mm、加载速度为5 mm/min时,土工格室整体拉力最大,为40.79 k N.
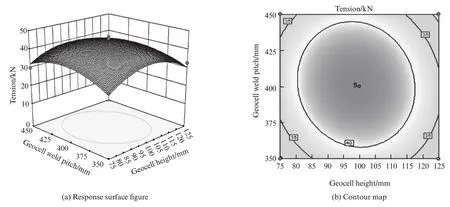
图9 格室焊距和格室高度对整体拉力的影响Fig.9 Influence of geocell height and geocel weld pitch on test tension
土工格室高度、焊距、加载速度对土工格室拉伸变形影响的响应面图如图10所示.由图10可见:各因素之间的交互作用相对显著程度,随着土工格室高度、焊距的增加,土工格室的整体位移变形呈现明显的增加趋势,而加载速度对位移影响较小.利用Design-Expert软件对3者进行对比分析,发现在加载速度为5 mm/min、高度为75 mm、焊距为400 mm的条件下,土工格室的整体抗拉性能最好.
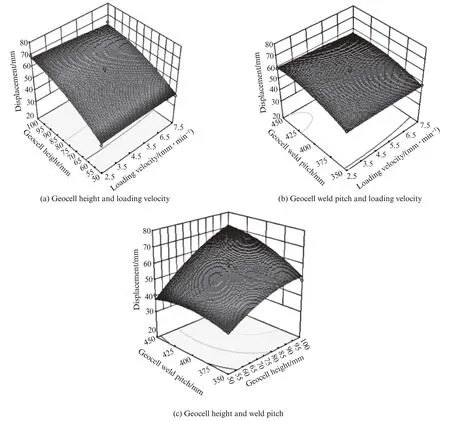
图10 不同因素对土工格室拉伸整体变形位移的影响Fig.10 Influence of different factors on the overall deformation and displacement of geocell tensile
3.3 试验验证
在格室高度75 mm、格室焊距400 mm及加载速度5 mm/min的条件下对土工格室双轴拉伸试验整体拉力和位移变形进行重复验证.分别选择4组拉力和位移的试验值与Design-Expert软件预测值进行比较,结果如表9所示.由表9可见:拉力的试验平均值为36.34 kN,软件计算值为37.42 kN,相对误差仅有2%;位移的试验平均值为58.51 mm,软件计算值为57.69 mm,相对误差为1.42%.计算值与试验值的误差较小,可以为土工格室拉伸整体拉力设计值的确定提供理论依据.
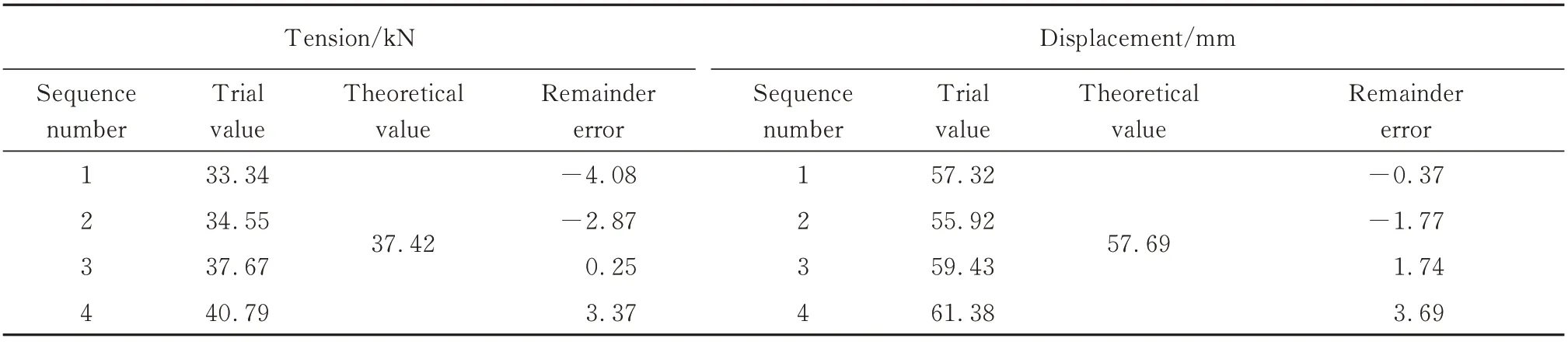
表9 模拟与试验结果对比Table 9 Comparison of simulation and test results
4 结论
(1)双轴拉伸试验可以真实反映土工格室整体受力和变形的特点,可以弥补现行测试方法的不足,是一种可靠的试验方法.
(2)双轴拉伸试验中高强土工格室的破坏均发生在节点处,在实际工程设计时,应关注格室整体抗拉承载力与节点抗拉承载力、条带抗拉承载力之间的匹配关系.
(3)土工格室的焊距增大到一定程度以后,整体抗拉承载力的提高并不明显.土工格室整体拉力随着土工格室高度、加载速度的增大而增大.
(4)对土工格室整体抗拉承载力的影响程度由大到小为:格室高度>格室焊距>加载速度.
