模糊集理论在造船企业库存控制优化中的应用

向子权，杨家其，向祖权，康熙沛

（武汉理工大学 交通与物流工程学院，湖北 武汉 430063）

0 引言

在造船企业的管理成本中，所需物资成本一般超过生产总成本的60%。对造船企业而言，物流大多以生产为中心而展开，但是造船企业的生产流程繁杂且不确定因素多，采购部门采购物资时难以精确把握，库存部门不易管理库存，因而造船企业库存一直居高不下。目前造船企业库存管理主要存在两个问题：一是物料仓库利用率问题。物料仓库空间有限，物资存储时间较长导致物资严重积压，使得仓库的利用率不高，很难满足现有生产及将来扩大生产的需要。二是库存部门存储成本问题。物资积压占用大量流动资金，不仅造船企业的存储成本要增加，抵御风险能力、适应市场能力以及企业的经营效益都要随之下降。若造船企业能最大化地降低库存，最快速地周转物料（零库存），则管理成本就能得到极大降低，占用的流动资金也将大量减少，利润会大幅度提高。所以，造船企业重视物资库存管理，其对于缩短物资周转时间，提升流动资金利用率等意义重大。

但是，在诸多情形下，因为造船企业库存控制缺少充足信息，加之生产过程繁杂且易变动，用概率理论不易准确预测需求数量，只能对可能的需求变化有一个模糊理解。因此，有学者尝试采用模糊数学方法来描述需求。因模糊集理论能较好地处理不确定性问题，已广泛应用在库存控制管理中。Kacpryzk[1]和Park[2]首次在库存管理中引进模糊数学，将库存成本当成模糊数解析经济订货批量模型。叶银芳[3]针对需求不确定的多销售商企业联合订购同种产品的库存管理问题，建立了允许缺货的联合订货EOQ模型。袁国强[4]针对不确定信息下的生产库存管理系统中的利润问题，提出了一个新的模糊VaR 优化方法。Mahuya Deb 和Prabjot Kaur[5]针对库存控制决策支持系统，为控制生产和供应，构建了神经模糊系统（NFS）。Wenfang YU[6]针对供应链管理中的库存居高不下问题，运用蚁群算法及模糊模型基本思想，提出了一种更加系统和改进的供应链库存优化模型。Zhan zhong[7]针对单个供应商及多个零售商组成的供应链库存成本问题，建立了一个双目标供应商管理模糊库存模型。Javad Sadeghi[8]研究了一个双目标供应商管理库存（BOVMI）模型，用于求解单一供应商和多个零售商的供应链问题，其中需求是模糊的，使用梯形模糊数（TRFN）表示模糊需求，采用几何重心法去模糊化。Chandra K和Jaggi[9]建立了一个具有斜坡型需求函数的变质物品模糊库存模型，通过最小化库存系统的总成本来确定最优的补货策略。利用三角模糊数在传统成本构成中引入一定程度的模糊性，并采用符号距离法对总成本函数进行解模糊。

综上所述，对不确定环境下呈现的各种可能性，模糊数学均能较好地表达库存控制问题，但是造船企业库存管理有其独特性，基于此，在不确定环境下采用模糊集理论探讨造船企业库存控制问题，建立模糊参数库存模型并优化求解。

1 模糊集理论

1.1 模糊集数学表达式

在造船企业库存管理过程中，所需物资数量巨大、物资品种繁多，加之库存管理复杂、时空差异大、机器障碍、订单撤销等一系列不确定因素都会增加不确定条件下的模糊性。造船企业在年底预测下一年需求时，这种情况更为突出。譬如对某物资预测数量为200 件左右，200 就是一个模糊数，其可能是190，也可能是210，最小为150，最大为250，取值范围可用区间[150,250]表示。此时是模糊需求，取值区间便是一个模糊集，可用符号D表示。任取模糊集中的一个数值，其皆有可能为未来的实际需求，但可信程度并不一样，中间的可能性要大些，两端的可能性要小些。为便于阐明可能性大小，先建立一个映射，令φx:D→[0 ,1]，其中，x ∈[L,U]=D(L ＜U)，φx∈[0 ,1] 。取D中任一数值，在[0 ,1] 中都有唯一数相对应，则D→[0,1]确定了D的模糊子集φx，φx称为D的隶属函数，或者D对φx的隶属度。如果φx=0.8，表明可能性为80%，φx=0.5，则表明可能性为50%。在研究库存控制优化问题时，通常采用梯形分布表示隶属函数，梯形分布分为三种：偏小型、偏大型和中间型，本文采用中间型，其隶属函数表达式如下：

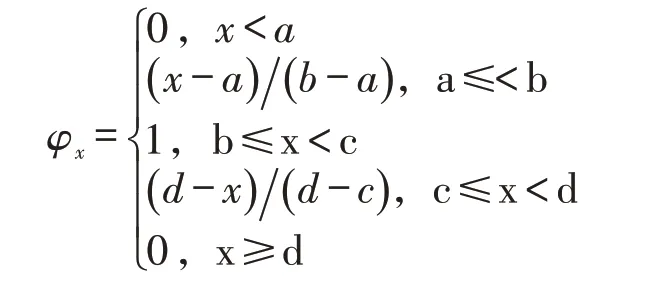
其图像如图1所示。

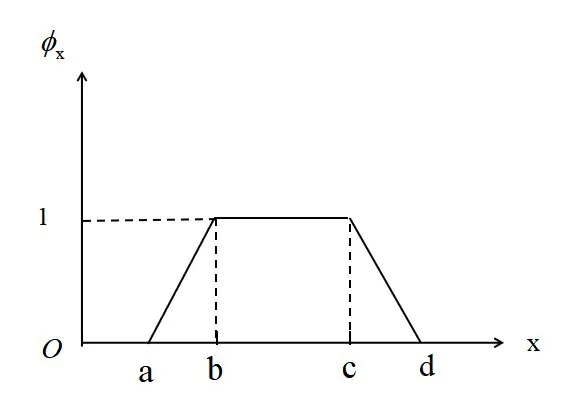
图1 梯形分布隶属函数图像

确定了模糊数D=[a,b,c,d] 的表达形式之后，若要比较模糊数大小，就应当进行解模糊，即明确模糊数的序。本文选取梯级平均综合表示法（gradedmean integration representation）解模糊[10]，若梯形模糊数为D=[a,b,c,d] ，则依据此方法解模糊值可表示为：

其中h表示任意水平隶属度，其取值范围为h ∈(0，1]。

1.2 模糊运算法则

梯形模糊数可进行加减乘除运算。令梯形模糊数D1=[x1,x2,x3,x4] ，D2=[y1,y2,y3,y4] ，其模糊数的运算法则如下：

（1）模糊加法：D1+D2=[x1+y1,x2+y2,x3+y3,x4+y4]；

（2）模糊乘法：D1×D2=[c1,c2,c3,c4] ，其 中c1=Min{xiyj} (i，j=1,4 )，c2=Min{xiyj} (i,j=2,3) ，c3=Max{xiyj} (i,j=2,3) ，c4=Max{xiyj} (i,j=1,4 )，当xi≥0,yj≥0,i,j ∈{1 ,2,3,4} 时，乘法运算可变更 为D1×D2=[x1y1,x2y2,x3y3,x4y4] ；

（3）模糊减法：D1-D2=[x1-y4,x2-y3,x3-y2,x4-y1]；

（4）模糊除法：D1D2=[d1,d2,d3,d4] ，其 中d1=Min{xi yj} (i,j=1,4 )，d2=Min{ xi yj} (i,j=2,3) ，d3=Max{xi yj} (i,j=2,3) ，d4=Max{xi yj} (i,j=1,4 )。当xi≥0,yj≥0,i,j ∈{1,2,3,4} 时，除法运算可变更为D1D2=[x1y4,x2y3,x3y2,x4y1] ；

（5）令α∈R ，当α≥0 时，α×D=[αx1,αx2,αx3,αx4]；当α ＜0 时，α×D=[αx4,αx3,αx2,αx1]。

2 造船企业库存控制优化模型

2.1 问题提出

以造船企业机电物资库存管理为例，经调研发现造船企业机电物资资金占用在1 万元以下的物资数量最多，占机电物资总数量的90%以上。该物资通常包括自制件、船舶用标准件或在国内供应商购买的常用零部件。此类物资采购较为容易，但是物资需求量大，而且需求数量不平稳，是一个模糊数，同时假定订货费用及保管费用也是模糊数。本文探讨在需求数量、订货费用及保管费用均不确定的情形下，运用模糊集理论建立多模糊数学库存模型，从而优化造船企业机电物资库存控制问题。

作出如下假设：

（1）订单瞬间到达，补充库存；

（2）消耗情况均与机电物资数量成正比。

2.2 多模糊库存模型建立及优化求解

针对造船企业机电物资库存问题，约定以下符号：

D：表示库存需要的机电产品数量，即D=[d1,d2,d3,d4] 。

Co：表示机电物资单位订货成本，即

Ch：表示机电物资单位保管成本，即

Q：表示订货量，一般为确定值。

M：表示每次运输费用，一般为确定值。

综上所述，库存总成本费用包含三项费用：订货费用、保管费用和运输费用，即：

其中，首项是订货费用，即单位订货成本Co乘以订货次数D/Q的积；中间项是保管费用，即单位保管成本Ch乘以平均库存水平Q/2 的积，本文采用Q/2来表示平均库存水平；末项是运输费用，即每次运输费用M乘以订货次数D/Q的积。

将上述各参数代入式（2）中并运用模糊运算法则，得总库存费用：

依据式（1）对式（3）进行解模糊，可以得到：

要在总费用最小的前提下，确定最优经济订货批量Q*。令，解之，可得到Q*，即：

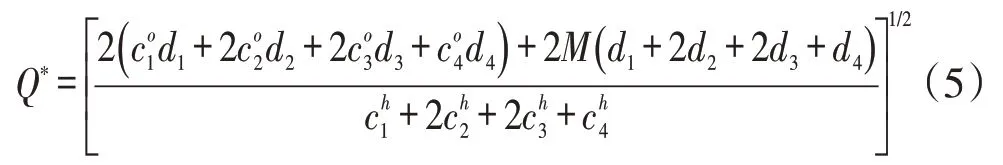
3 实例分析

为验证多模糊参数库存模型的可行性，依据某造船企业机电物资入库及出库数据进行验证。因占用资金超过1万元的机电物资需求量比较固定，因此重点考虑资金占用在1 万元以下的机电物资。经调研发现，这些机电物资存放时间较长，且物资采购批量大，物资采购与生产部门需求不一致，导致积压大量库存。其从2019年1月1日到2019年10月31日，入库数量为5 010件，出库数量（生产上的需求数量）为4 325件。假定一次性采购完毕，每次订货费用约280 元/次，单位保管费用约10 元/月，运输成本为一确定值，取860元/次。

因此可算出该造船企业实际费用开支如下：订购费：280（元）；平均库存量：5 010/2=2 505（件）；保管费：2 505×10=25 050（元）；运输费：860（元）；总费用：280+25 050+860=26 190（元）。

应用模糊数学库存模型进行优化并求解。依据2018年底生产部门合理预测，M=860，可令：

将其代入式（5），得到Q*≈996，即最佳经济订货批量为996 件。此时优化后的费用如下：采购次数：4 325÷996≈4.34（次），取整后的次数为5 次；订购费：280×5=1 400（元）；保管费：996/2×10=4 980（元）；运输费：860×5=4310（元）；总费用：1 400+4 980+4 310=10 690（元）。

优化后的模糊库存模型计算的总费用比实际费用低26 190-10 690=15 500（元），虽然订购费用和运输费用增加，但是库存保管费用大幅度下降，从25 050 元降至4 980 元，下降幅度达80.12%，库存总费用从26 190元降至10 690元，下降幅度达59.18%。

若需求数量是模糊的，单位订购费用及单位保管 费 用 是 确 定 的，即D=[4 200 ，4 300，4 350，4 600]，Co=280，Ch=10，M=860，代入式（5），可得到Q*≈995。

若全部条件皆为确定值，即D=4 325 ，Co=280 ，Ch=10 ，M=860 ，代入式（5），可得到Q*≈993。结果表明任一模糊参数变更，都会影响最佳经济批量。

4 结语

由于造船企业的复杂性和多变性，本文运用数学模糊集理论来处理库存管理，以机电物资为例，构建了梯形模糊库存模型，研究了在每次运输成本确定时，模糊环境下的需求数量、单位订购成本及单位保管成本下的订货批量问题。本文研究的是多模糊参数的造船企业库存控制问题，某一参数若条件足够充分可明确其值，则该参数此时就是一个确定值。若所有条件足够充分则全部参数都属于确定值，此时变成了确定条件下的订货批量问题。虽然造船企业库存控制实际环境模糊，但最终给出的是确定的最优决策。实例计算结果表明，应用梯形模糊集数学理论来解决造船企业库存管理问题合理可行，能有效控制资金及减少库存费用。