弧形闸门重心和重力矩计算方法

2021-12-30段东旭廖玉海

人民珠江 2021年12期

兰钦，段东旭，廖玉海，程忠

(中国电建集团中南勘测设计研究院有限公司，湖南长沙 410014)

弧形闸门重力矩是影响启闭力的重要因素[1]。与平面闸门不同，弧形闸门结构复杂，其重心不易准确获取。SL 74—2013《水利水电工程钢闸门设计规范》[2]和NB 35055—2015《水电工程钢闸门设计规范》[3]均只简单地给出了弧门启闭力计算的表达式，其中重力矩采用自重与力臂之积表示，但并没有给出弧门自重及不同开度下的力臂计算式[3-4]。长期以来，弧门各构件自重均简化成规则的矩形板计算，重力力臂通常采用经验公式，即近似认为重心位于弧门全关时总水压力作用线上距支铰中心0.80或0.85倍半径处，弧门任意开度下的重力力臂则通过角度换算得到[5-6]。该经验公式综合考虑了弧门实际外荷载和主框架合理刚度比，依据等安全度水平设计理念，并结合大量工程经验得到，概念清楚、计算简便，在工程界得到了普遍的应用。但是该公式未考虑弧门设计时实际重量分布，特别是对于有局部加重或者异型结构弧门，必然存在一定的误差。

随着计算机三维辅助设计平台的开发和普遍应用，设计人员只需要建立弧门的三维模型，便可以获取弧门自重及重心的精确值。许多学者已直接采用数值模拟的方法直接计算出较高精度的内力和启闭力[7-9]。但是目前这种方法模型建立过程较复杂[10]。设计人员往往需要将采用平面体系法设计的弧形闸门在三维辅助设计平台上建立模型，得到重心后再进行启闭力计算和布置优化，计算和优化效率不高，不易得到弧门结构和启闭机布置的全局最优结果。此外，三维辅助设计平台需要耗费较大计算机容量，计算时间也较长。如何通过较简单的方法获取弧门重心，并将弧门结构计算与启闭机布置优化结合，以便得到全局最优结果，具有重要的研究价值。

本文试图从理论上推导弧门重力、重心和重力矩的解析公式，分析弧门重心的2个参数(半径rG、倾角θG)对弧门启闭力的影响，在此基础上提出计算弧门重心的简易法，结合工程实例编制相应的计算程序，将计算结果与经验公式、三维模型的结果进行比较，验证计算方法的合理性和优越性，为类似弧门设计提供参考。

1 弧门重量及重力矩

弧门任意开度下主要构件自重及重力矩可采用积分[11]计算，下面具体说明。图1中，在柱坐标下与竖直方向成θ角度处取弧门某构件体积微元dV,其外半径为Ri，径向高度为δi，环向包角为dθ，垂直于纸面方向即Z向宽度为Bi，钢材的密度为ρ，重力加速度为g。

图1 弧门重心及重力矩计算

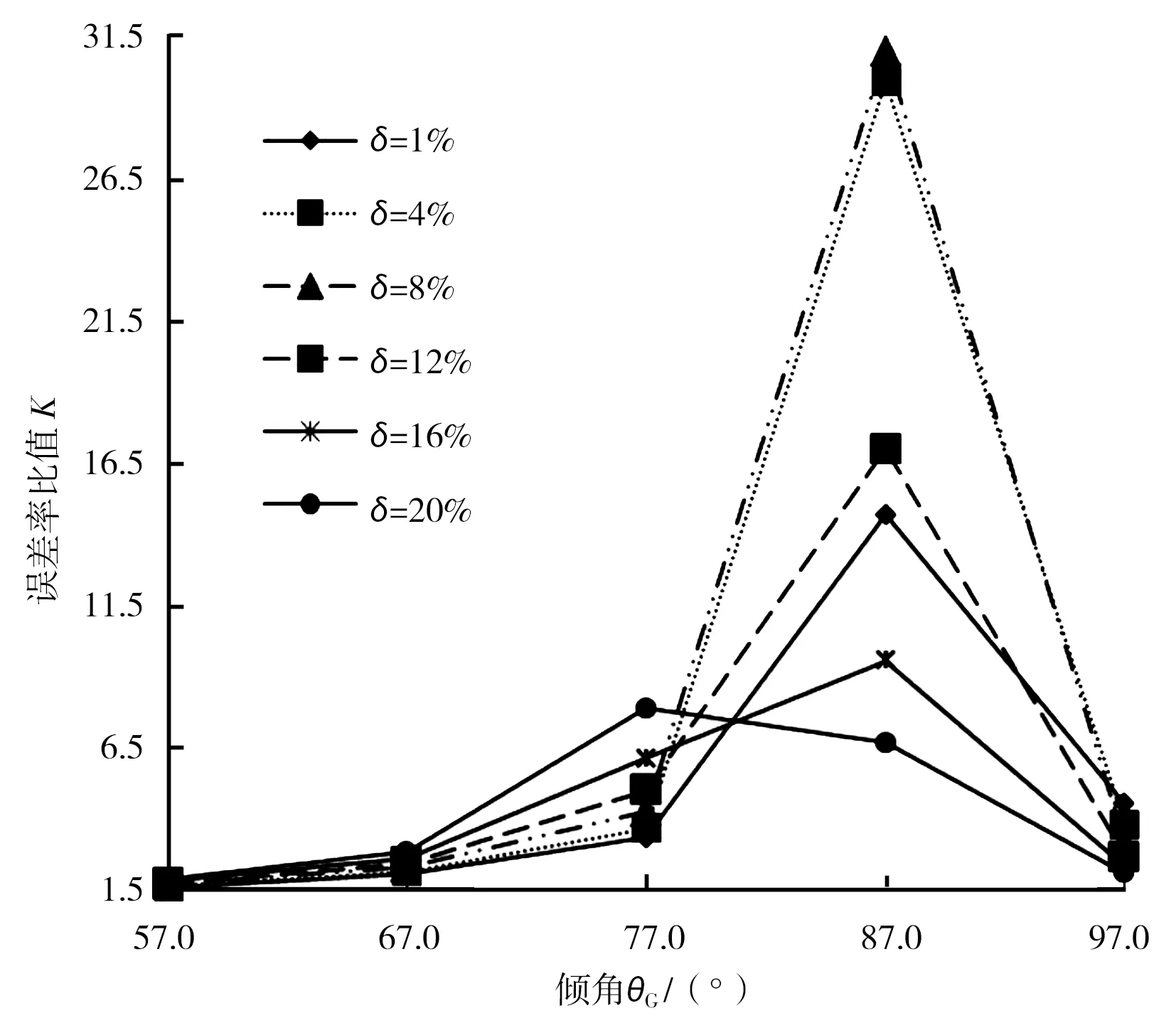
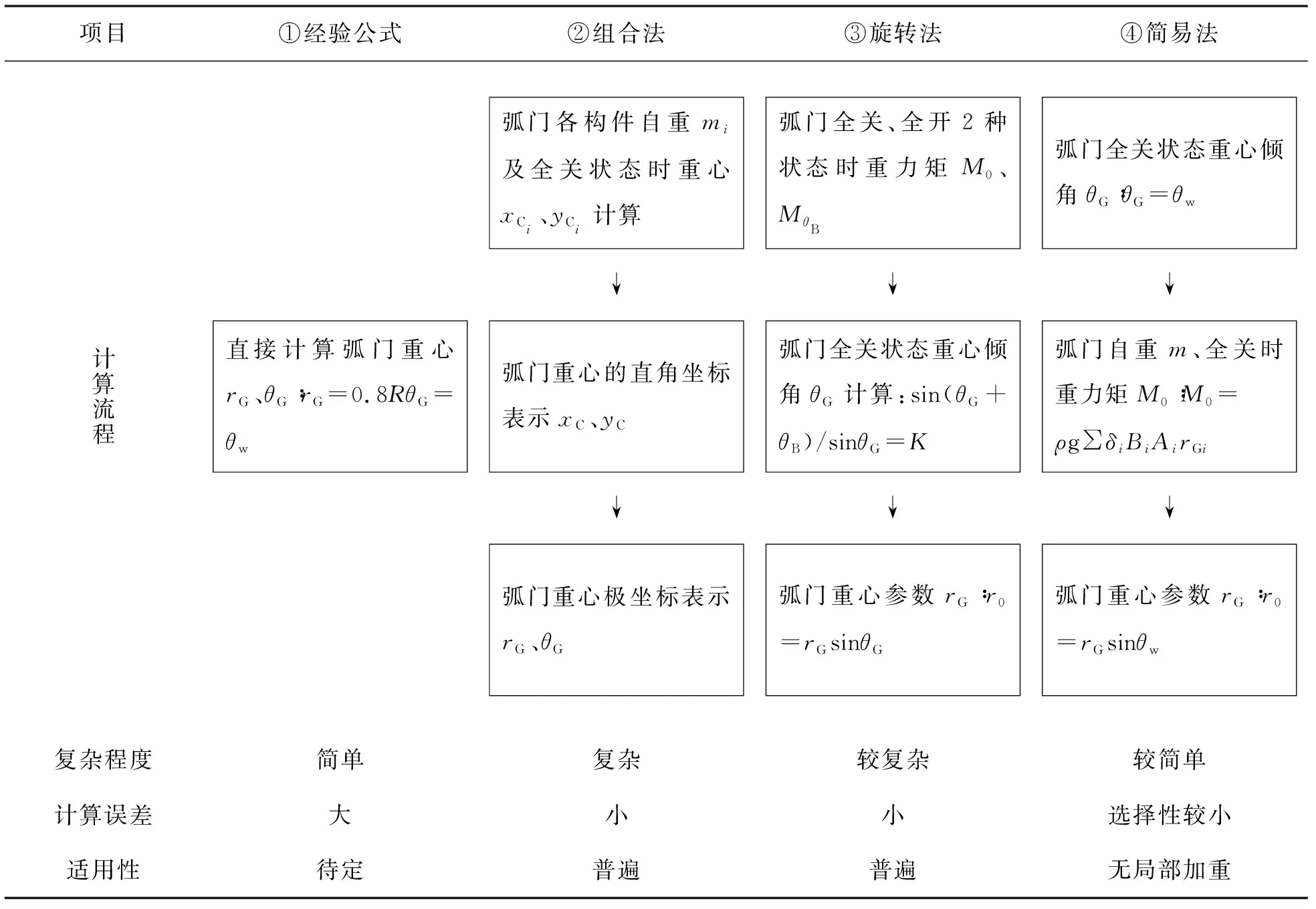
由于δi

(1)

(2)

mi=ρδiBiAi

(3)

Mi=ρgδiBiAirGi

(4)

则弧门重量及该开度下的重力矩为：

m=∑mi=ρ∑δiBiAi

(5)

M=∑Mi=ρg∑δiBiAirGi

(6)

式(5)、(6)为弧门自重、重力矩的计算通式。设计人员可以根据弧门开闭的角度变化利用式(6)计算出弧门不同开度下的重力矩。但是每一种开度下的重力矩均需采用这个复杂的公式分别计算，计算过程复杂、计算量较大。而且得不到弧门的重心，使弧门及其启闭机系统优化过程仍存在盲目性，优化效率低下。如果能够通过某种较简单的方法得到弧门的重心，则可结合式(5)直接计算出不同开度时的重力矩。此时，弧门任意开度Δθ时重力矩可表示为：

MΔθ=mgrGsin(θG+Δθ)

(7)

式中rG——弧门重心到支铰中心的距离；θG——弧门全关状态下重心-支铰中心连线与竖直方向的夹角。

式(6)、(7)实际上是2种不同的计算重力矩的方法，其计算流程列于表1。

表1 弧门重力矩计算流程

2 弧门重心计算方法

2.1 组合法

图1中，当闸门处于全关状态时，首先计算出各构件对其主惯性轴的重心值x0Ci，然后通过坐标变换计算出在直角坐标系xoy下的重心(xCi,yCi)，最后计算出弧门重心(xC,yC)，则极坐标表示的重心坐标为[12]：

(8)

(9)

(10)

2.2 旋转法

弧门任意2种不同开度j、k时弧门的重力力臂rj、rk为：

(11)

(12)

开度j、k时重心-支铰中心连线与竖直方向的夹角分别为θGj、θGk，则开度j、k时弧门的重力力臂rj、rk亦可表示为：

rj=rGsinθGj

(13)

rk=rGsin(θGj+Δθ)

(14)

联立式(7)—(10)得：

sin(θGj+Δθ)/sinθGj=f

(15)

式中，f为常系数，f=Mk/Mj。显然，式(15)中除θGj为未知量外，其他均为已知量。若能证明函数f(x)=sin(x+Δθ)/sinx在本文所述问题边界条件下是单调的，就能通过式(15)求出唯一的θGj，进一步代入式(13)，就可以求出rG。至此，弧门的重心就确定了。

2.3 简易法

从以上的分析可知，弧门重心由半径rG和倾角θG2个参数确定，本节将分析2个参数对弧门启闭力的敏感性，进而提出只考虑较敏感因素的弧门重心简易计算公式。定义参数a的相对误差为：

(16)

式中，a0为参数a的真实值，a1为参数a的计算值。则在半径rG和倾角θG同等相对误差δ条件下，弧门任意启闭状态下半径rG计算误差所引起的启闭力相对误差δFr与倾角θG计算误差所引起的启闭力相对误差δFθ的比值K可表示为：

(17)

由式(17)可知，启闭力相对误差比值K的大小与相对误差δ、倾角θG、开度Δθ有关，与半径rG无关。对于露顶式弧门，图2为弧门零开度(Δθ=0)时启闭力相对误差比值K与倾角θG关系曲线，从图中可以看出，对于不同的相对误差δ，K值总体上大于1；当θG在87°左右，K总体上达最大，最大值高达500左右；只有当θG>110°时，K才略小于1；对于倾角θG和开度Δθ取可能值，K值总体上大于1。

事实上，对于按等安全度水平设计且无局部加重块的弧门，夹角θG的真实值与θw(θw为弧门总水压力作用线与竖直方向的夹角)相差不大，可进一步地取θG∈[θ1+θB/4,θ1+θB/2]，代入易得出θG∈[57°,97°]。此时，K总大于1.5，即半径rG总体上比倾角θG更敏感。另外，实际设计时半径rG的相

图2 启闭力相对误差比值K与倾角θG关系曲线

对误差往往远大于倾角θG的相对误差或者两者的相对误差均很小。在不同的相对误差δ1、δ2(δ1<<δ2)时，启闭力相对误差的比值K将远大于1。综合以上因素，露顶式弧门启闭力相对误差比值K将远大于1，即半径rG对弧门启闭力的影响比倾角θG大得多；对潜孔式弧门和水闸露顶式弧门，也可得出类似的结论。从以上分析来看，对于按等安全度水平设计且无局部加重块的弧门可取θG≈θw，代入式(13)便可以计算出半径rG，该计算方法为简易法。

2.4 几种计算方法的比较

除三维模型外，共有4种求解弧门重心的方法，其中组合法和旋转法均是通过理论推导而来，只是计算思路不同，合称为解析法。各计算方法流程及其比较列于表2。

3 算例验证

3.1 典型弧门模型及参数

算例①：潘口溢洪道露顶式弧门孔口宽度20.0 m，孔口高度为18.327 m，下游无水，面板曲率半径为23.0 m，转动铰高度为10.327 m，门叶高度为18.8 m，闸门重力为3 000 kN。转动铰摩阻力力臂为0.425 m，水封摩阻力力臂为23.0 m，水封上托力的力臂为20.55 m。已知闸门能依靠自重下门，采用经验公式计算时挡水状态时启门力最大，此时启闭力力臂10.946 m。

表2 弧门重心及重力矩各种计算方法流程及比较

算例②：潘口泄洪洞潜孔式弧门孔口宽度8.0 m，孔口高度为10.0 m，面板曲率半径为16.0 m，转动铰高度为13.10 m，门叶高度为10.15 m，闸门重力为2 334.5 kN。转动铰摩阻力力臂为0.35 m，水封摩阻力力臂为16.0 m，顶、底水封上托力的力臂分别为16.0、9.2 m。已知闸门能依靠自重下门，采用经验公式计算时全开状态时启门力最大，此时启闭力力臂11.05 m。

相关参数：钢材密度为7 850 kg/m3，泊松比为0.31；铰轴滑动摩擦系数为0.1，侧水封压缩量为4 mm，水封线压力为p=58 N/cm，摩擦系数为0.5；底水封长度为110 mm，厚度为15 mm，闸门挡水状态时的压缩量为5 mm，弹性模量为6 MPa。

3.2 重心解析计算法合理性验证

分别采用经验公式、三维模型、组合法、旋转法对实例中弧门重心做了计算。其中，三维有限元模型中利用APDL程序[16-20]获取重心，组合法、旋转法采用MATLAB编程[21-23]实现。考虑到结构的特殊性，弧门有限元模型钢结构构件均采用壳单元，止水部分采用摩擦单元[19-20]。其中，案例①模型共有节点71 609个，单元35 125个(图3)；案例②模型节点53 609个，单元30 095个(图4)。4种方法的计算结果及比较见表4、5，计算中将三维模型的计算结果作为真实值。

图3 算例①有限元模型

图4 算例②有限元模型

表3 弧门各构件单元类型

表4 算例①4种方法计算结果及比较

表5 算例②4种方法计算结果及比较

从表4、5可以看出：采用经验公式计算时，倾角θG的最大相对误差为3.78%，半径rG的最大相对误差为25.18%，倾角θG的误差均远小于半径rG的误差，两者最小相差约1倍；采用组合法、旋转法计算的结果相当，最大相对误差为7.58%，总体上比经验公式的小很多。与占据大容量内存和模型建立复杂的三维平台相比，组合法、旋转法只需编制1个小程序就可以实现，更方便设计者掌握和使用。此外，依据组合法、旋转法编制的计算程序，能够与闸门结构和启闭机系统布置优化程序结合，从而实现对弧门的全局优化[10]设计。相比较而言，旋转法不需要分别计算各构件的重心，亦无须坐标转换，比组合法更简便。

综上，经验公式可以用于弧门启闭力估算和启闭力随开度的变化规律分析；解析法兼具精度高和通用性强突出优点，与组合法相比较，旋转法计算过程较简单，是弧门重心较优的计算方法。

3.3 2个参数对启闭力影响分析

采用3种方法计算的3.1节2个算例弧门最大启门力及由θG、rG相对误差所引起的启门力相对误差见表6、7。从表中可以看出，采用经验公式计算时，启闭力最大相对误差为23.52%；采用旋转法计算时，启闭力最大相对误差为6.05%，比经验公式的结果精度高很多，这与第3.2节重心计算时的结论是一致的；采用这2种方法计算时，由倾角θG所引起的启闭力最大相对误差为0.81%，由半径rG所引起的启闭力最大相对误差为23.66%，2种方法启闭力相对误差结果呈现相同的规律，即由半径rG引起的启门力相对误差远大于由倾角θG引起的启门力相对误差，最小相差约1个数量级。这表明，对于弧门启门力而言，半径rG为敏感因素，倾角θG为非敏感因素；采用经验公式对弧门启闭力估算和启闭力随开度的变化规律分析是可行的。

表6 算例①2个参数误差对启闭力影响

表7 算例②2个参数误差对启闭力影响

3.4 重心简易计算法适用性分析

从2.3节的计算分析来看，采用简易法计算弧门重心从理论上是可行的。表8列出了采用简易法计算时弧门半径rG的计算结果，从表8可以看出，当采用简易法对两弧门重心进行计算时，半径rG最大相对误差仅为10.15%；与经验公式的计算结果相比精度提高约1倍；与旋转法的计算结果相比，半径rG相对误差相差不大，但计算量却减少很多。这表明，当弧门无加重时，采用简易法计算重心是简易可行的，这与2.3节的理论分析是一致的。