基于二元非线性拟合的溢洪道宽顶堰流量系数公式研究及应用

闫志方，贾云飞，王 宇

(1.广东珠荣工程设计有限公司，广东 广州 510610；2.广州开发区财政投资建设项目管理中心，广东 广州 510000；3.南京水利科学研究院水文水资源与水利工程科学国家重点实验室，江苏 南京 210029)

堰流流量系数是溢洪道及水闸等泄水建筑物泄流能力计算中的关键参数，当前国内外学者在堰流流量系数的计算方面已有大量研究：毛昶熙[1]从水力学基本原理研究计算公式的合理性，并以模型试验资料验证，给出了堰闸淹没泄流的流量系数表达式和大孔径隧洞泄洪流量的计算公式；张绍芳[2]在系统地研究低堰溢流的水力特性的基础上，给出通用于不同堰型和堰高、水头范围的溢流能力的计算方法；林孟程[3]通过对宽浅式溢洪道低堰体型研究，得出宽浅式溢洪道低堰流量系数随堰顶水头及定型水头的变化规律；Issam A.Al-Khatib等[4]通过实验室水槽模型试验并利用多元回归模型对数据拟合得到矩形复合宽顶堰流量系数及流速系数计算公式；Mohamad Reza Madadi等[5]通过实验室水槽模型试验研究了梯形宽顶堰迎水面坡度对流量系数的影响，并通过曲线拟合得到流量系数与迎水面角度的函数关系；Nourani Bahram等[6]应用数值模拟的方法分别引入2种智能模型计算宽顶堰流量系数，并对2种模型参数有效性及计算结果进行了评估和对比；马欣等[7]通过水工模型试验研究单宫V型迷宫堰不同布置方案的过流能力，并对试验研究成果进行数学回归拟合分析，得到可直接用于工程设计的V型迷宫堰过流能力计算公式。

水库设计中，溢洪道控制段控制着水库的水位和下泄流量，是溢洪道的咽喉[8]，其常用堰型有宽顶堰、实用堰，其中宽顶堰相对实用堰流量系数较小，但其结构简单，施工方便，地基应力分布比较均匀，整体稳定性较好，因此在泄流量不大的中小型水库中得到了较广泛应用。

宽顶堰流量系数计算在溢洪道宽顶堰泄流能力计算中起着至关重要的作用，工程设计中主要采用现行水利行业规范[9](以下简称“SL规范”)中流量系数表、电力行业规范[10](以下简称“DL规范”)或水力计算手册[11](以下简称“手册”)中的经验公式进行计算。SL规范中的流量系数采用与相对上游堰高P1/H及底坎形状有关的二维表格，考虑因素比较全面，但要计算泄流能力的水位-泄流量曲线时，需要进行P1/H与r/H或cotθ(Δx/Δy)2个参数的二维线性内插，计算较为繁琐；DL规范及手册中流量系数是与相对上游堰高P1/H单变量有关的函数，计算时可编辑公式快速计算，运用方便，但是由于考虑因素单一，会导致计算精度较低或应用范围较窄。

齐清兰等[12]根据SL规范中流量系数表数据应用最小二乘回归分析法拟合了有坎宽顶堰流量系数的经验公式，计算精度高于DL规范公式，但是由于其拟合的流量系数公式是不同r/H或cotθ(Δx/Δy)值下的单变量P1/H公式，进行水位-泄流量曲线计算时参数r/H是跟水头H有关的变量，仍需进行一次r/H线性内插，计算不够方便；单长河等[13]采用二元非线性回归分析法对多个数学模型进行分析，结合实测资料得到了无坎宽顶堰流量系数的经验公式，克服了查表法多次内插带来的不便，但是其拟合的经验公式是以翼墙型式及宽度的收缩程度为自变量的表达式，与常用的规范及手册上的自变量差别较大，使用仍不够方便。为方便SL规范流量系数表格使用，本文将利用SL规范中数据采用二元非线性拟合的方法对数据进行拟合得到底坎为圆角的宽顶堰流量系数公式m=f(r/H，P1/H)，将其与电力规范公式比较，并对两者计算误差进行分析讨论。

1 流量系数计算公式拟合

1.1 拟合原理

有理函数属于简单函数，它虽比多项式复杂，但用其近似表示函数时，却比多项式灵活，更反映函数的一些特性[14]。因此本次二元非线性拟合将采用二元有理函数作为拟合函数。二元有理拟合就是寻求二元有理函数：

(1)

使之满足下列插值条件：

r(xi,yj)=fij,(i=0,1,2,……m,j=0,1,2,……n)

(2)

式中P(x,y)、Q(x,y)——二元多项式；fij——样本数据在(xi,yj)点的值。

吴晓韵[15]在逼近二元表格函数时，选用了二元有理函数，通过使性能指标J0(a)=极小来求解各项待定系数ai。本文根据吴晓韵[15]的思路选用式(3)对数据进行拟合，函数表达式为：

(3)

式中a1，a2，……，a9——待求系数。

令x=r/H，y=P1/H，则式(3)可表示为：

(4)

1.2 基础数据

本研究所用样本数据为SL规范中表A.2.3-1、A.2.3-2数据，由于底坎为直角或斜面时cotθ=0的情况与底坎为圆角时r/H=0为同一种情况，因此本次将底坎为直角或斜面时cotθ=0条件下的m值表数据与底坎为圆角时的表格数据结合作为本研究的样本数据，见表1。

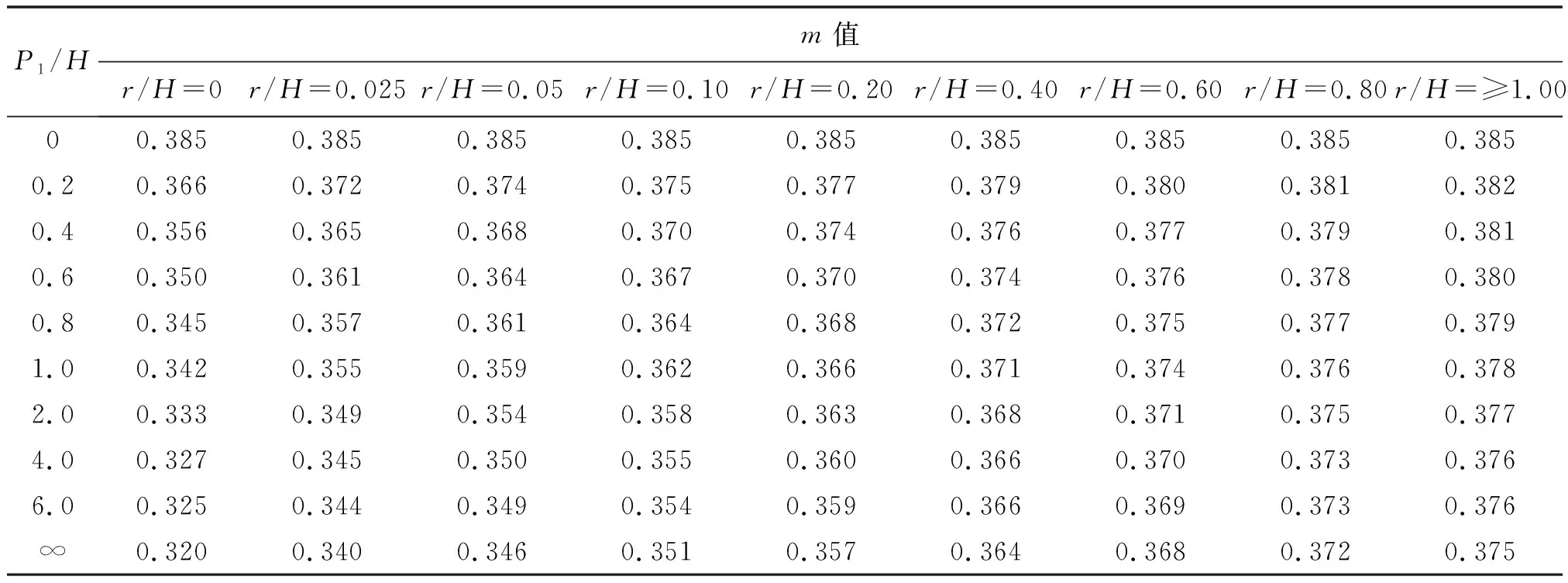
表1 底坎为带圆角的宽顶堰流量系数m值

1.3 拟合结果

因基础数据在P1/H∈(6，+∞)区间无明确数据，故本文进行拟合时仅采用P1/H∈[0，6.0]对应样本数据。经拟合，求解出式(4)中各待定参数值及其相关性见表2，拟合函数曲面图见图1。

表2 函数待定参数值、标准误差及相关性

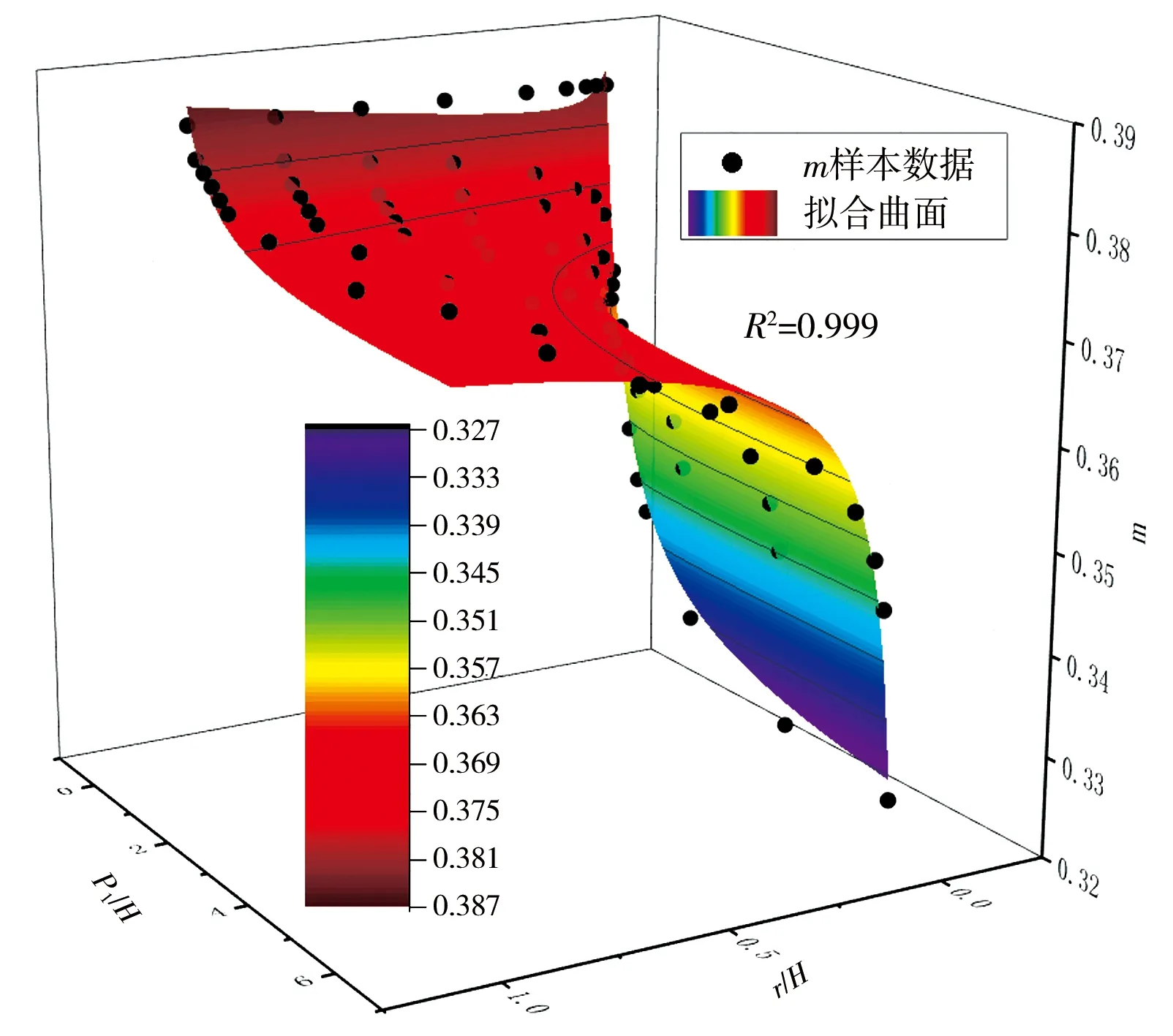
图1 拟合函数曲面图

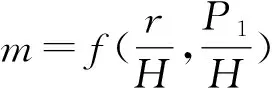
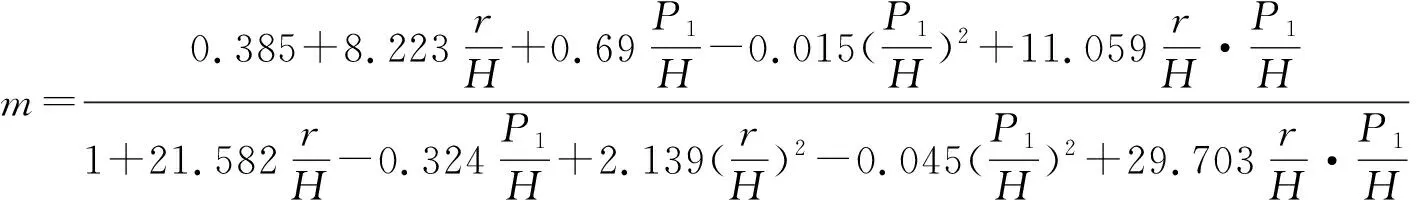
(5)

式中m——宽顶堰流量系数；H——堰顶水头，m；P1——宽顶堰坎高，m；r——坎顶圆角半径，m。各参数见图2。

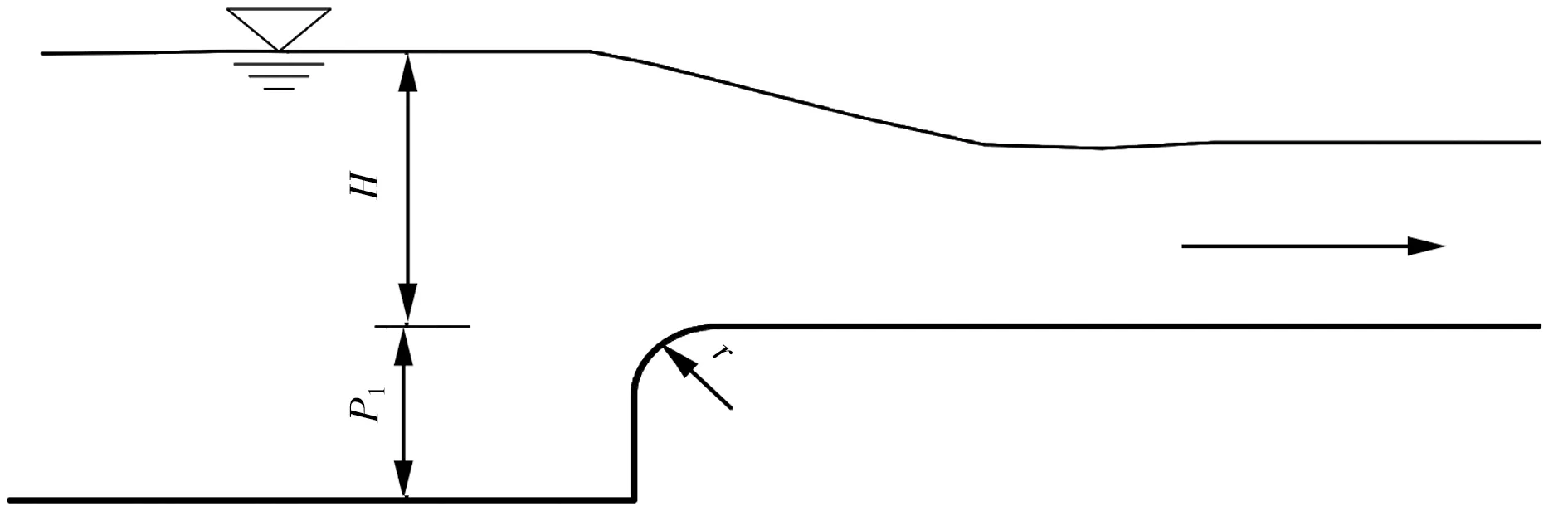
图2 宽顶堰示意

2 公式比较与误差分析

2.1 公式验证比较

将SL规范表A.2.3-1、A.2.3-2数据及其线性插值结果作为标准值，分别用本次拟合公式及DL规范计算公式计算结果与标准值进行对比。DL规范宽顶堰流量系数m计算公式见式(6)、(7)。式中各参数同式(5)。

进口底坎为方角时：

(6)

进口底坎为圆角时：

(7)

本次分别对各公式在r/H=0、r/H=0.025、r/H=0.05、r/H=0.10、r/H=0.20、r/H=0.40、r/H=0.60、r/H=0.80时，对应P1/H=0～6时计算结果进行比较，计算结果见图3。由图3计算结果可看出：①拟合式(5)计算出的流量系数m在r/H各取值下与SL规范表格标准值趋势相同，且计算点与标准曲线基本重合；②DL规范式(6)和(7)计算流量系数m在r/H<0.20时，均位于标准值曲线之上，此时DL规范公式计算结果偏大，随着r/H增大，计算点与标准曲线差距逐渐减小；③r/H=0.20时计算m值与标准曲线基本重合且优于式(5)计算结果；④r/H>0.20时，计算流量系数m均位于标准值曲线之下，此时DL规范公式计算结果偏小，随着r/H增大，计算点与标准曲线差距逐渐增大。

综上分析，总体而言拟合式(5)计算结果优于DL规范式(6)和(7)计算结果。

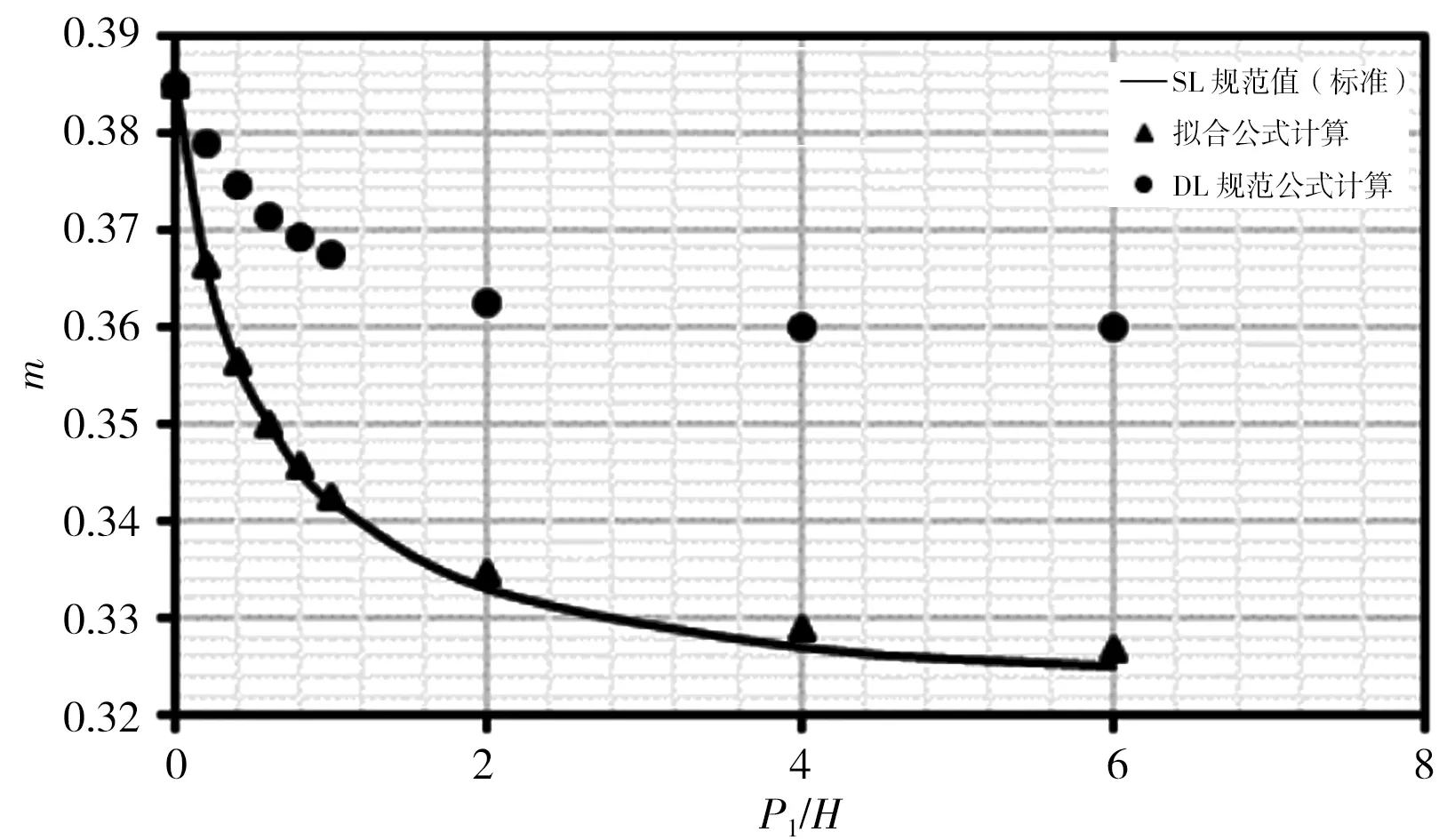
a)r/H=0

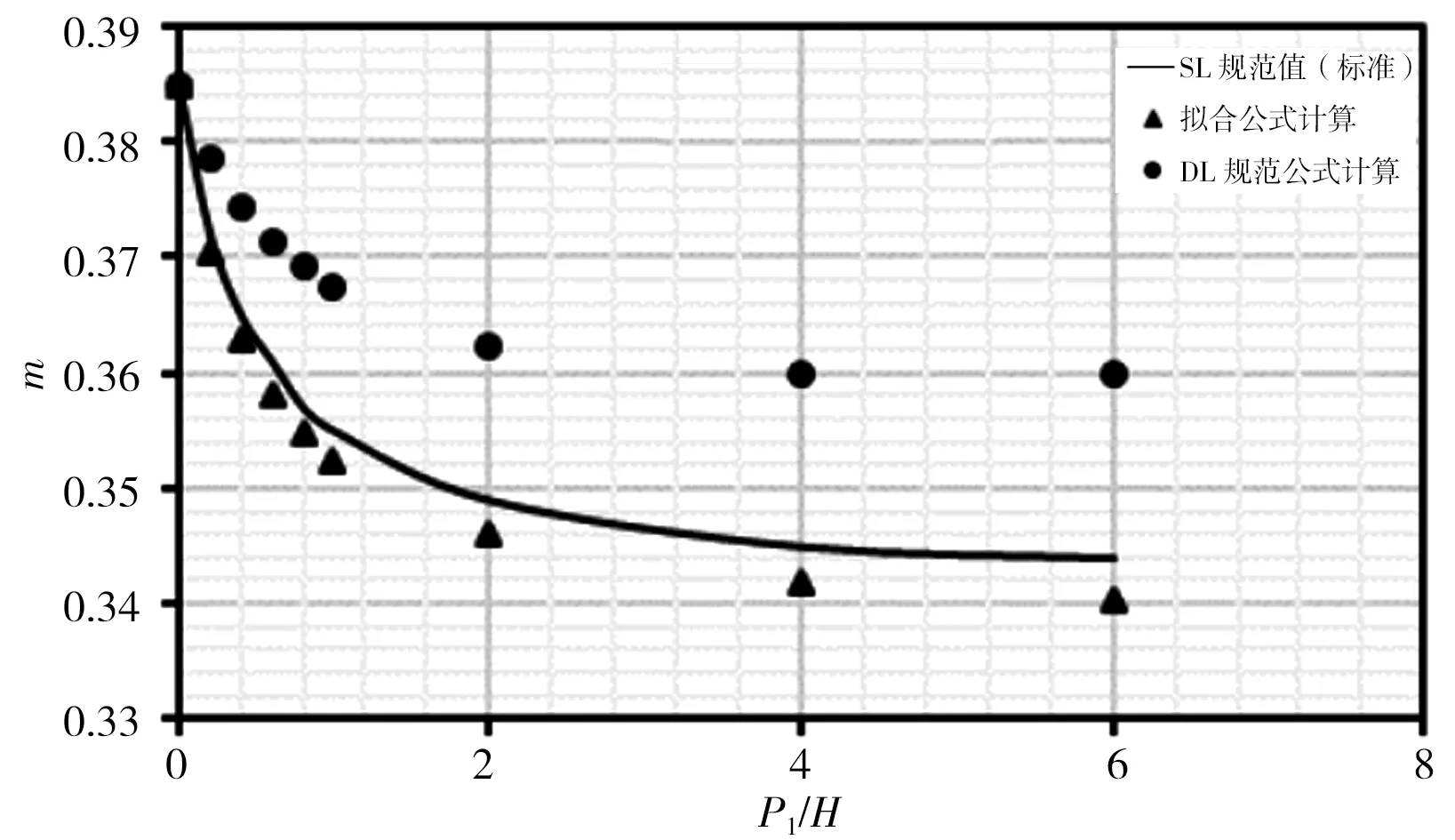
b)r/H=0.025

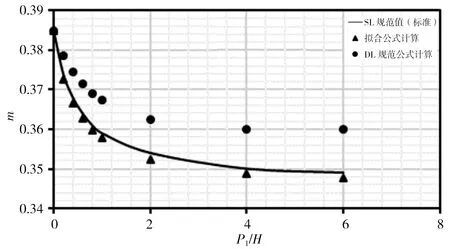
c)r/H=0.05

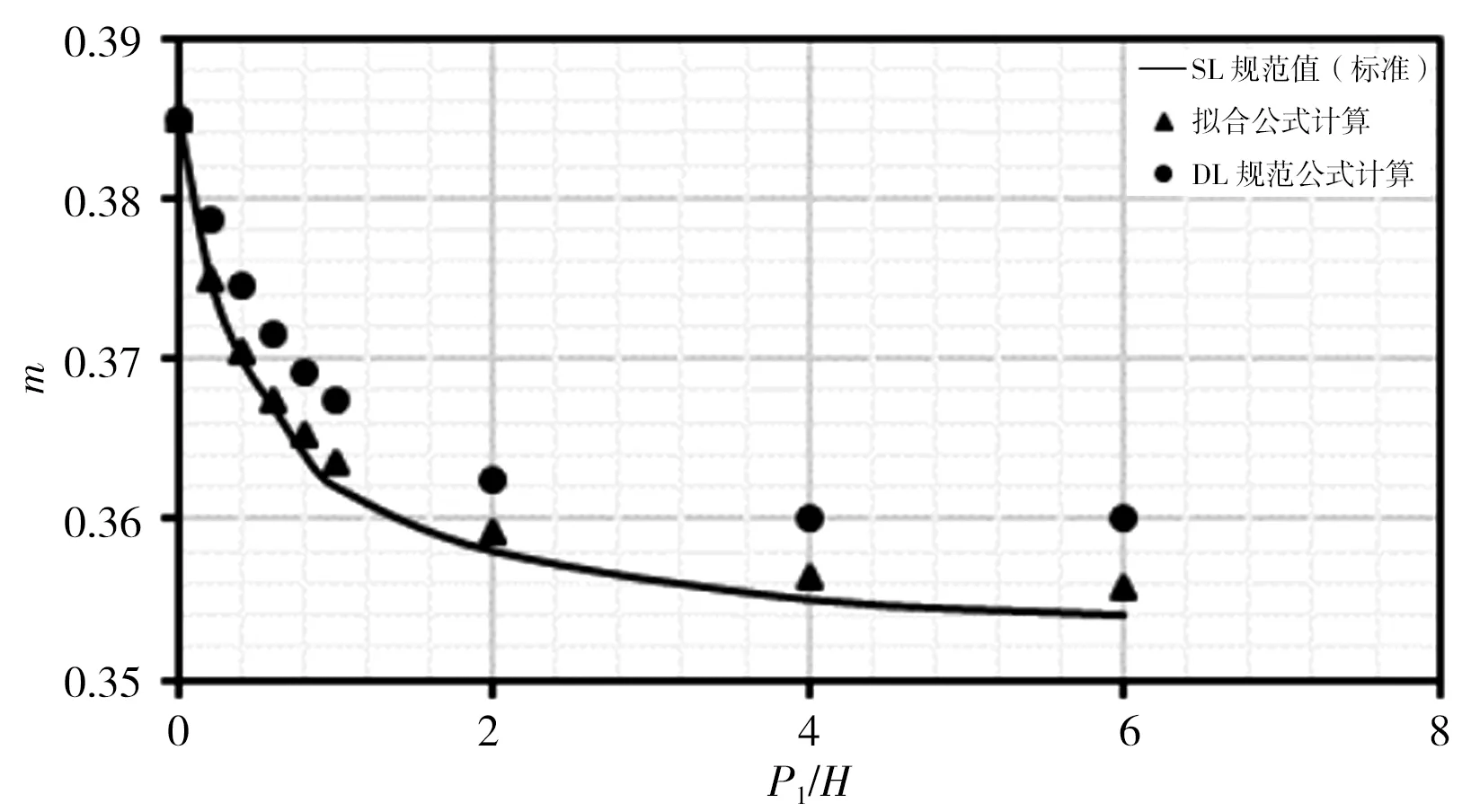
d)r/H=0.1

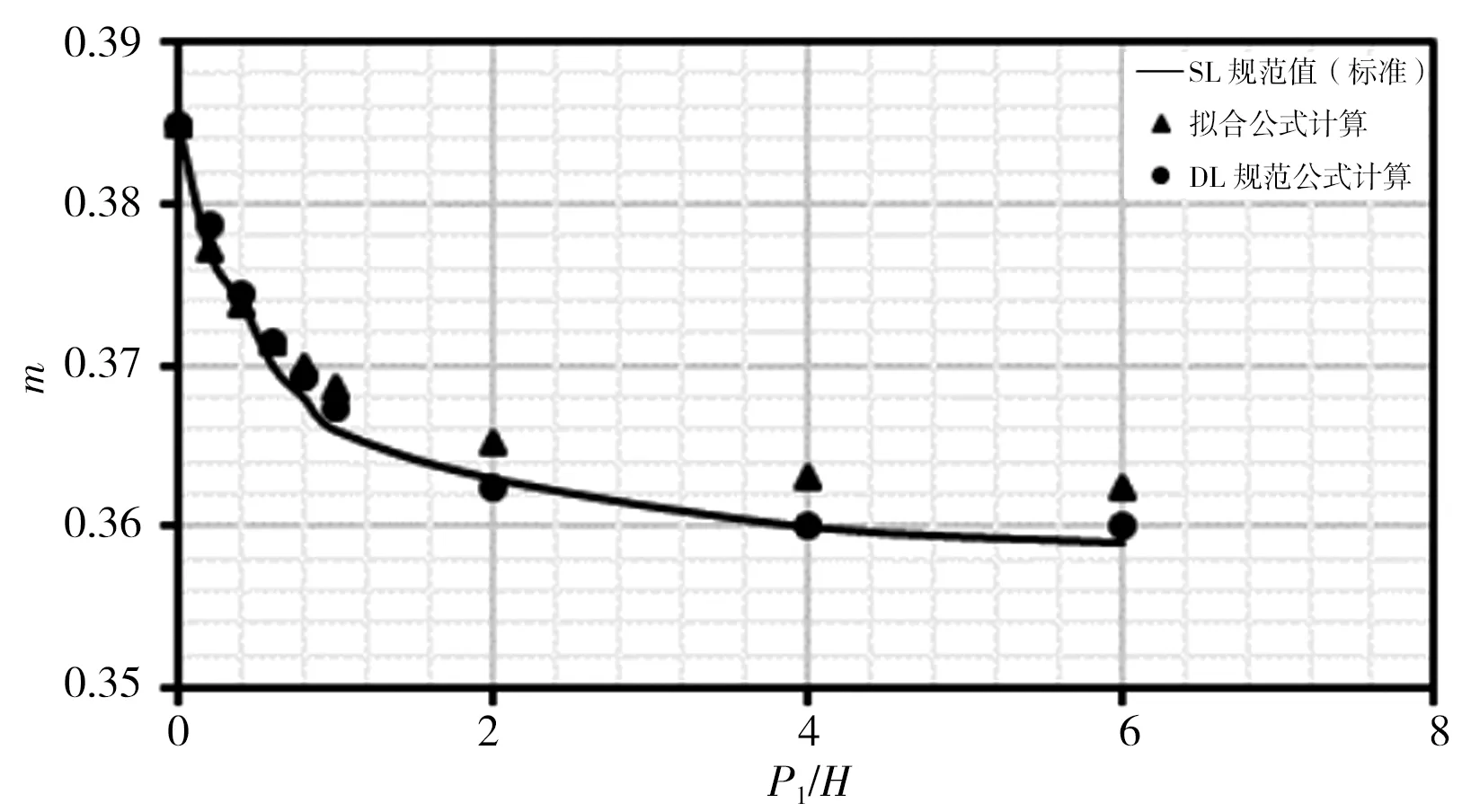
e)r/H=0.2

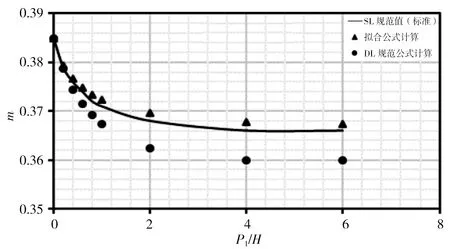
f)r/H=0.4

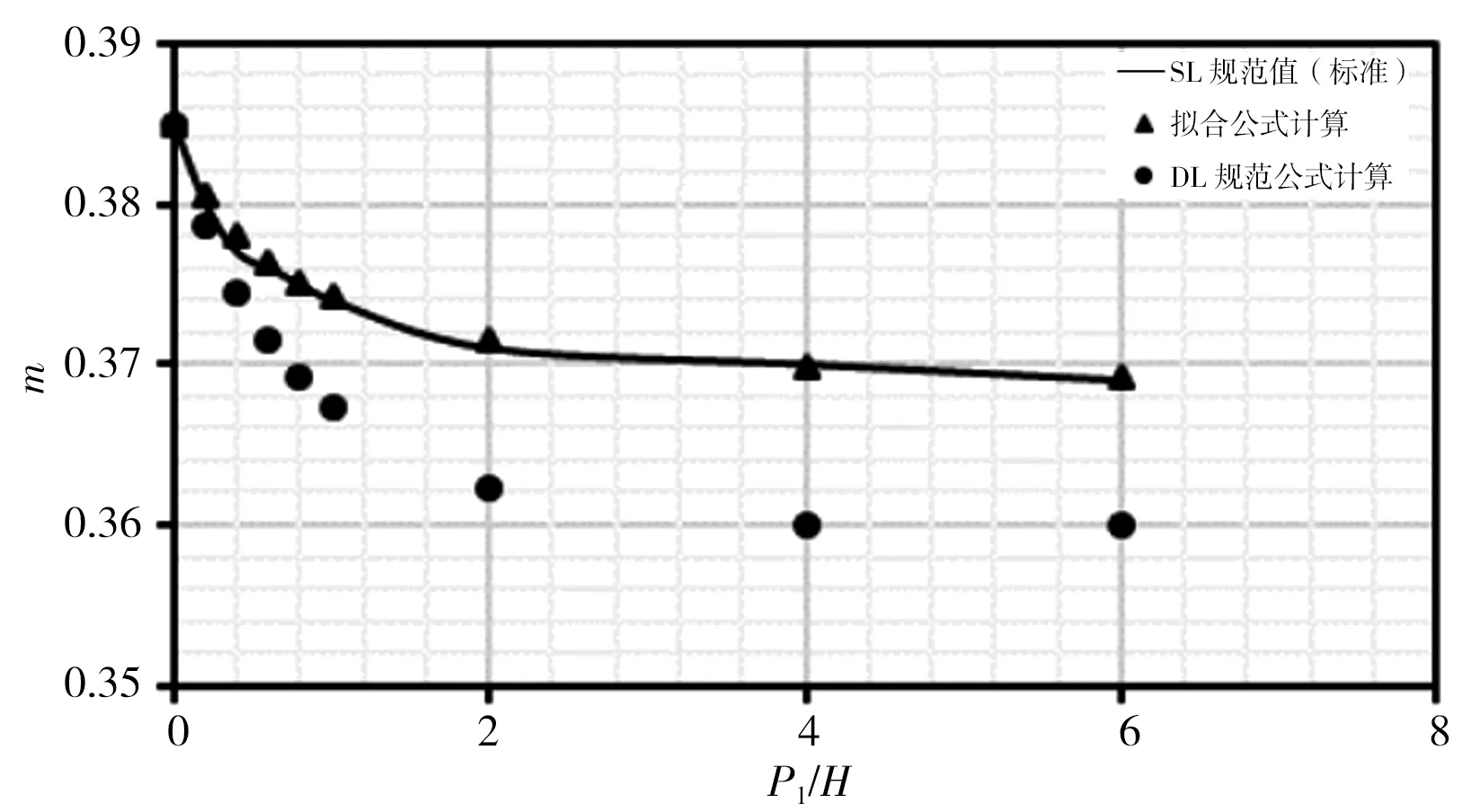
g)r/H=0.6

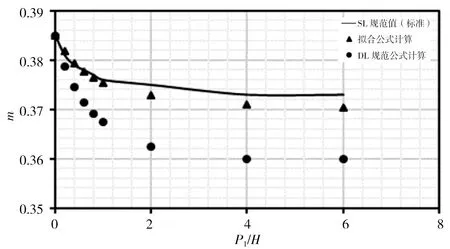
h)r/H=0.8

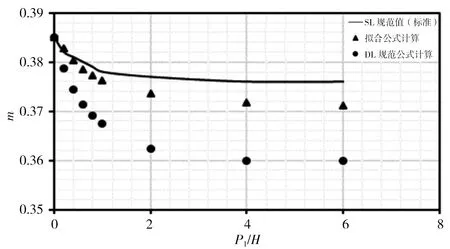
i)r/H≥1.0

2.2 计算误差分析

为定量比较拟合式(5)与DL规范公式的计算精度，需对两公式计算结果进行误差比较。戴文鸿等[16]在比较稳定河道计算方法时采用了差异比(DR)、相对误差(RE)、几何平均偏差(GAD)3个指标，本文将采用这3项指标来分析比较计算值与标准值之间的误差。指标计算式如下：

(11)

(12)

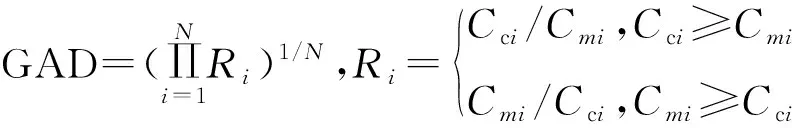
(13)

式中Cc——计算值；Cm——标准值；N——数据组数。

DR越接近1表示计算值与标准值越接近；RE越接近0表示计算值与标准值越接近；GAD越接近1表示计算值与标准值越接近。

经计算，不同r/H值下拟合式(5)与DL规范公式计算结果的平均相对误差、平均差异比及平均几何平均偏差对比见图4。从图中可看出如下结果。

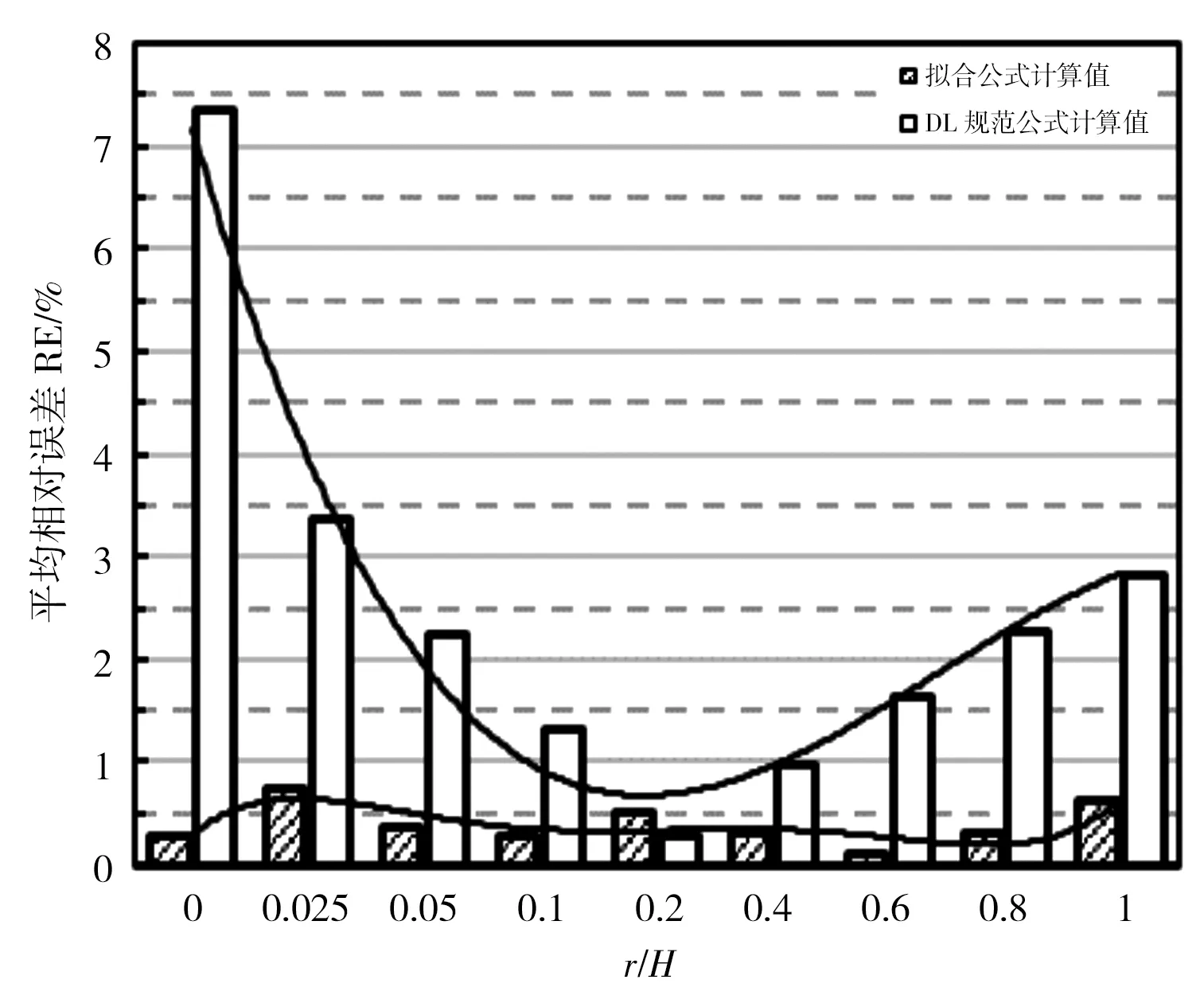
a)平均相对误差

b)平均差异比

c)平均几何平均偏差

a)平均相对误差：拟合式(5)平均相对误差在r/H各取值下均在1%以下，且在0.5%上下变化。DL规范公式平均相对误差在r/H<0.20时从7.36%逐渐减小到1.33%，该范围内平均相对误差在1%以上；r/H=0.20时平均相对误差达到最小值0.26%；r/H>0.20时平均相对误差从0.97%逐渐增大到2.83%，该范围内平均相对误差在3%以内。

b)平均差异比：拟合式(5)平均差异比在r/H各取值下均在1±0.01以内。DL规范公式平均差异比在r/H<0.20时从1.07逐渐减小到1.01，最大变幅+0.07；r/H=0.20时平均差异比达到最小值1.002；r/H>0.20时平均差异比从0.99逐渐减小到0.97，最大变幅-0.03。

c)平均几何平均偏差：拟合式(5)平均几何平均偏差在r/H各取值下均在1～1.01以内，最大变幅+0.01。DL规范公式平均差异比在r/H<0.20时从1.07到1.01逐渐减小靠近1.00，最大变幅+0.07；r/H=0.20时平均差异比达到最小值1.003；r/H>0.20时平均差异比从1.01到1.03逐渐增大偏离1.00，最大变幅+0.03。

综上分析：从整体水平上拟合式(5)各误差指标变化范围较小，且均在较优的范围内；DL规范公式各误差指标变化范围较大，在r/H<0.20时偏离最优值较大，在r/H=0.20时最接近最优值，在r/H>0.20偏离最优值相对较小。因此拟合式(5)在r/H各取值下均适用，DL规范公式仅在r/H≥0.20时较适用。

3 拟合公式应用实例

选取贵州省某水库溢洪道设计作为实例，采用拟合式(5)进行计算，并与查SL规范表格计算值进行对比。贵州某水库溢洪道由引渠段、交通桥段、控制段、泄槽段、消力池段和海漫段等部分组成，溢洪道全长226.83 m，其中引渠段长47.41 m，交通桥段长10 m，控制段长15 m，泄槽段长92.05 m，消力池段长28 m，海漫段长34.37 m。溢洪道控制段堰型为有坎宽顶堰，坎高P1=1.50 m，堰顶高程为892.00 m，与正常蓄水位平齐。泄槽段坡比1.0∶2.3，全段无变坡，宽度由17.50 m收缩为12 m。消力池型式为底流消能，底板高程851.50 m，池深3.50 m，池长28.00 m。

设计计算分别选取坎顶圆弧半径r=0、r=0.5P1=0.75 m、r=P1=1.5 m 3种型式，每种型式计算堰顶水头范围为0.2～15 m系列计算各流量系数。计算结果见表3。

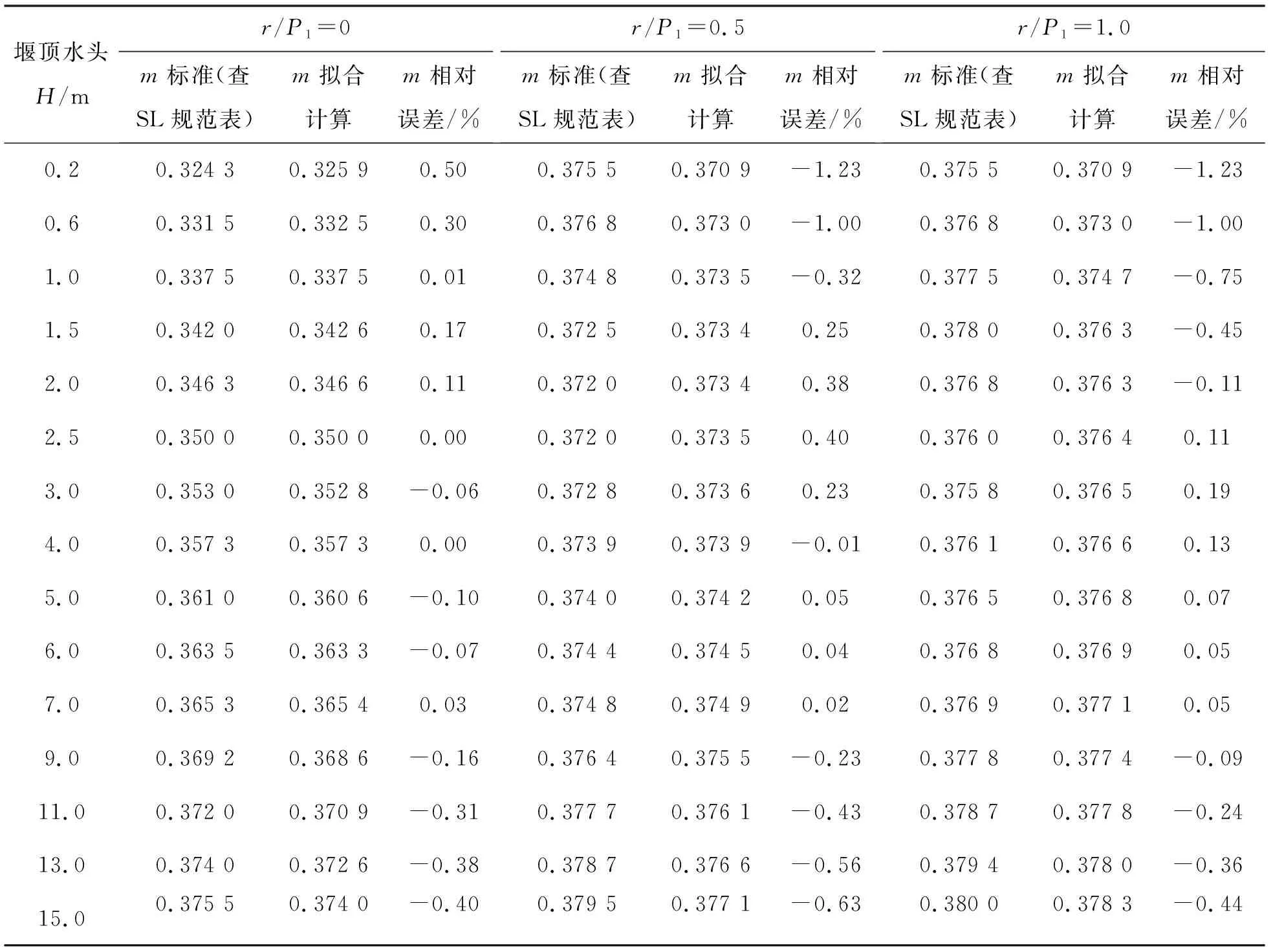
表3 不同圆角半径各堰顶水头下流量系数计算结果

将上表m标准值作为x坐标，对应m拟合计算值作为y坐标绘制于直角坐标系，见图5。从图中看出，r/P1=0时各点基本与“计算=标准”线重合；r/P1=0.5及r/P1=1.0时各散点均匀分布于“计算=标准”线附近，且大部分位于±1%误差线之间，仅有个别点在-1%误差线外，但较接近-1%误差线。分析其原因，位于-1%误差线以外的点为堰顶水头H较小时的计算结果，当H较小且P1/H>6时将超出拟合式(5)的样本范围，在样本数据范围外式(5)计算精度难以保证。

因此，在工程设计中当P1/H≤6时可应用式(5)替代查SL规范表A.2.3-2计算宽顶堰流量系数；在P1/H>6时须对计算的结果进行分析，若坎高P1不大，P1/H>6时堰顶水头H亦较小，此时式(5)计算结果偏小，在工程上偏安全，亦可用式(5)计算结果近似替代查SL规范表的值。

图5 实例验证

4 结论

a)选取SL规范表A.2.3-1、A.2.3-2数据作为样本数据，应用二元有理插值函对数据进行拟合得到溢洪道宽顶堰流量系数的二元函数表达式m=f(r/H，P1/H)，该公式可避免查表多次内插的繁琐工作。

b)经对拟合公式及DL规范公式进行验证比较，拟合公式计算结果优于DL规范公式计算结果。

c)经对拟合公式及DL规范公式计算结果的平均相对误差、平均差异比及平均几何平均偏差三误差指标比较，拟合公式在r/H各取值下均适用，DL规范公式仅在r/H≥0.20时较适用。

d)选取某水库溢洪道设计作为实例，经过对计算结果分析，在工程设计中可应用拟合公式替代查SL规范表计算宽顶堰流量系数。