力-热-磁耦合场中碳纳米管振动问题研究

贺 璞，邓庆田，李新波

（长安大学理学院，陕西西安 710064）

0 引 言

近年来，纳米材料的性能越来越受到关注，其超强的物理、化学和机电性能在各种技术领域得到了广泛的应用.其中碳纳米管作为纳米材料中非常重要的成员，由于其独特的结构特性和纳米尺寸在电学、化学和力学等方面具有许多优异的性能.Eringen［1］提出了考虑小尺度效应影响的非局部弹性理论，这种理论极大地推动了碳纳米管研究的进度，国内外的研究者们基于非局部弹性理论和梯度弹性理论对碳纳米管的力学行为展开了广泛的研究［2-7］.

Zhao等［8］基于 Von Karman几何非线性和非局部Timoshenko梁理论，研究了磁场对嵌入纳米管非线性振动尺寸灵敏度的影响，结果表明，高磁通抑制了纳米管的非线性振动，在高磁通条件下，非局部效应可以忽略；Habibi等［9］研究了电磁弹性纳米材料在热环境中与尺寸相关的自由振动；Tang等［10］通过非局部应变梯度理论研究了泊松比和厚度对纳米管振动特性的影响；Jalaei等［11］研究了热环境下轴向激励载荷和磁场作用下温度相关的Timoshenko功能梯度纳米梁的动态不稳定性；Dini等［12］基于湿-热弹性理论和Eringen非局部理论，建立了均匀弯曲的Euler-Bernoulli梁模型，分析了在磁场作用下输流弯曲双壁碳纳米管的湿热振动和稳定性；Zhen等［13］研究了粘弹性纳米管在纵向磁场作用下的自由振动，包括非局部参数、结构阻尼系数、材料长度尺寸参数和纵向磁场对系统固有频率的影响；Malikan 等［14］与 Malikan 和 Eremeyev［15］的工作则是聚焦于存在内部和外部粘弹性的碳纳米管的振动行为，并且进一步研究了挠曲对压电纳米管内部粘弹性的影响.

由近年来的研究可知，碳纳米管的粘弹性基础、荷载、温度场和电磁场都会对纳米管的性能有所影响，国内外相关的研究也有很多，而多场耦合情况下的分析却很少见.本文采用统一应力应变梯度弹性模型，对置于Kelvin-Voigt粘弹性基础上的Timoshenko碳纳米梁进行了粘弹性阻尼、小尺度效应和力-热-磁耦合的研究.

1 应力应变梯度弹性Timoshenko碳纳米梁模型

1.1 Timoshenko碳纳米梁

置于Kelvin-Voigt粘弹性基础上的Timoshenko碳纳米梁模型如图1所示.考虑碳纳米管处于力-热-磁耦合场环境中.

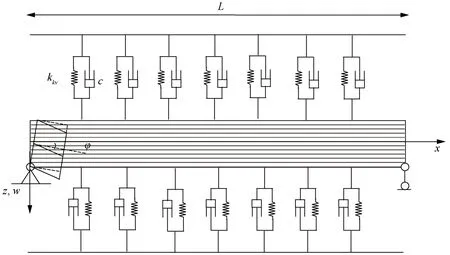
图1 粘弹性基础上的Timoshenko碳纳米梁

根据Timoshenko碳纳米梁理论，其轴向应变和切应变分别为：

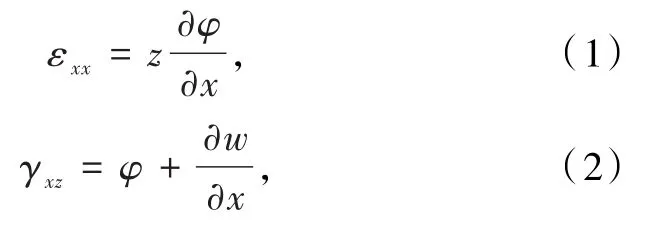
式中φ是截面因弯曲而旋转的角度.

1.2 统一应力应变梯度弹性模型

基于Eringen非局部理论和梯度弹性模型，得到统一应力应变梯度弹性模型，其本构关系为：

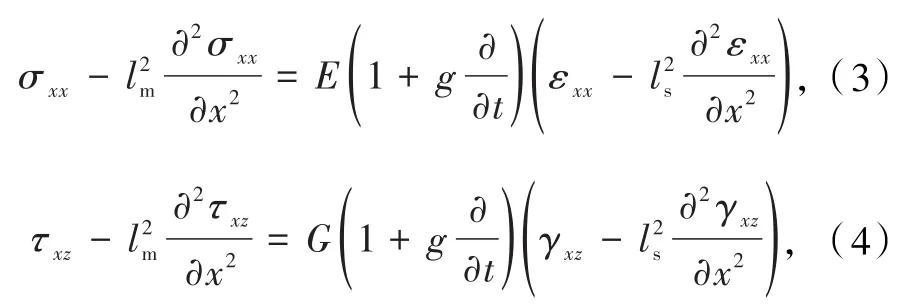
式中t为时间，σ和τ为应力张量，g为粘弹性阻尼系数，lm为非局部积分模型中的材料常数，ls为梯度弹性模型中的材料常数，E和G为弹性模量和剪切模量.

根据热弹性力学理论，由温度变化引起的轴向力（Nt）可表示为［16］

式中αx为轴向热膨胀系数，T为温度变化量，ν为泊松比，A为碳纳米管的横截面积，E为弹性模量且与温度无关［17］.

由纵向磁场在x、y和z方向引起的洛伦兹力分别为：

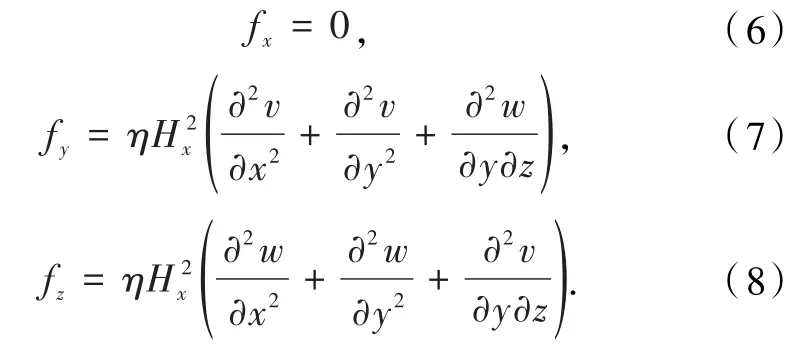
考虑平面变形假设，只存在z方向的洛伦兹力可简化为

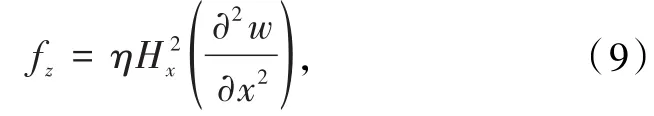
式中η为磁导率，Hx是x方向的磁场强度.

粘弹性基础采用Kelvin-Voigt模型进行描述为

式中q为粘弹性基础带来的均布荷载，c为阻尼系数，kkv为弹簧刚度.

非局部弯矩（M）和横向剪力（Q）可定义为：

由式（1）～（4）、（11）和（12）可得M和Q的表达式为：

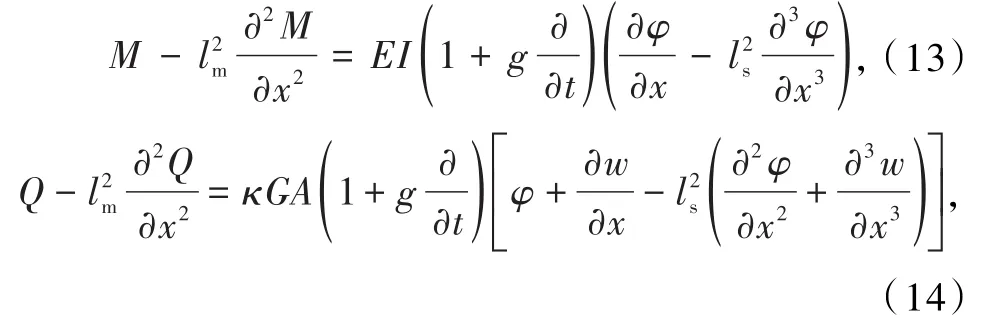
式中I为截面惯性矩，κ为剪切修正系数.结合式（5）、（9）和（10），考虑外部阻尼和轴向初始应力的运动方程可表示为：

式中ρ为密度，σ0为轴向初始应力，m为单位长度质量，C1为与位移速度有关的粘滞阻尼系数，C2是与旋转速度相关的粘滞阻尼系数.

将式（15）和（16）两边对x积分的表达式代入式（13）和（14），得到Q和M的表达式为：

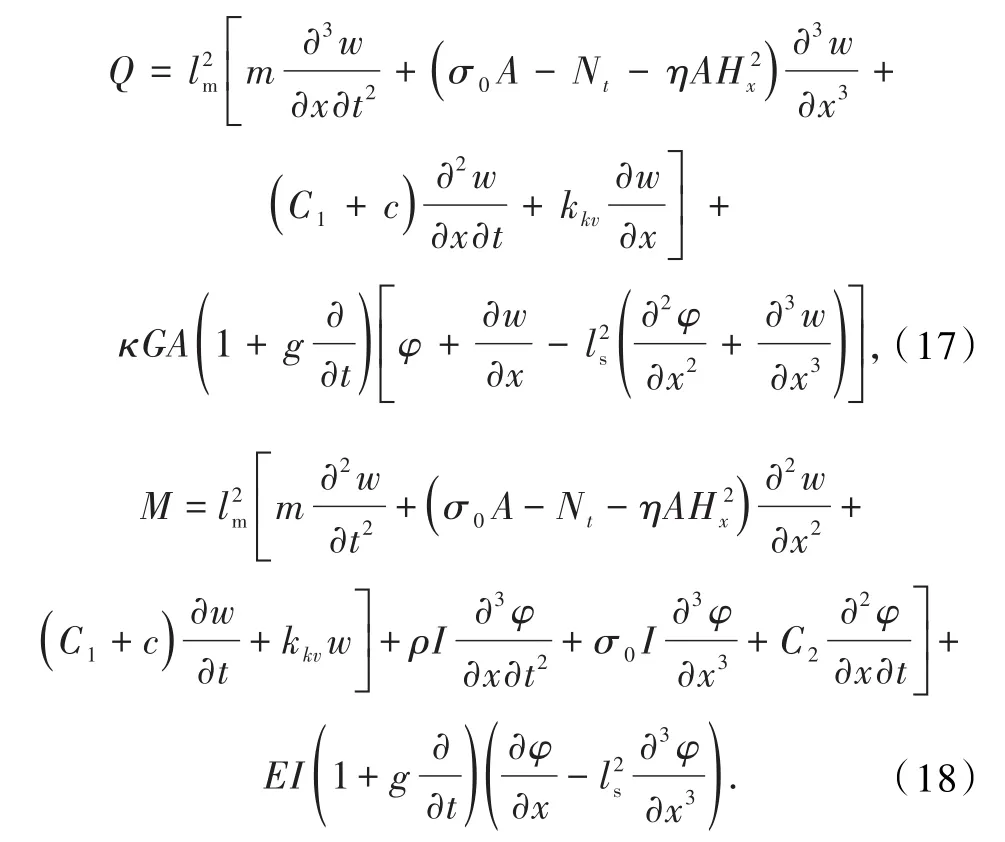
将式（17）和（18）代入式（15）和（16）中可得耦合方程表达式为：

1.3 简支碳纳米管控制方程求解

通过分析国内外对碳纳米管的研究，简支边界条件符合其受力状态，可以将其边界条件简化为简支边界条件.对于不同的边界条件只需要改变位移函数，代入式（19）和（20）中进行计算，此方法仍然适用.考虑简支边界条件的碳纳米梁，其位移函数可表示为：

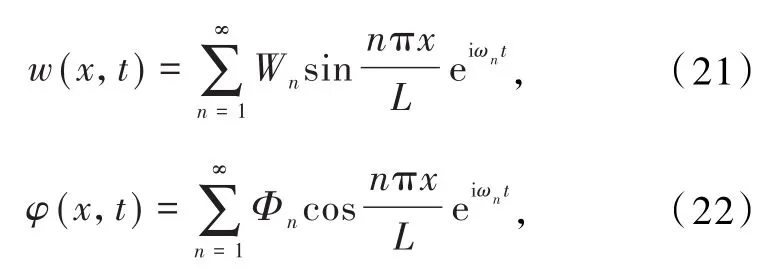
式中Wn与Φn为振幅，n为模态阶数，ωn为振动频率.将式（21）和（22）代入式（19）和（20）中，化简后可得：

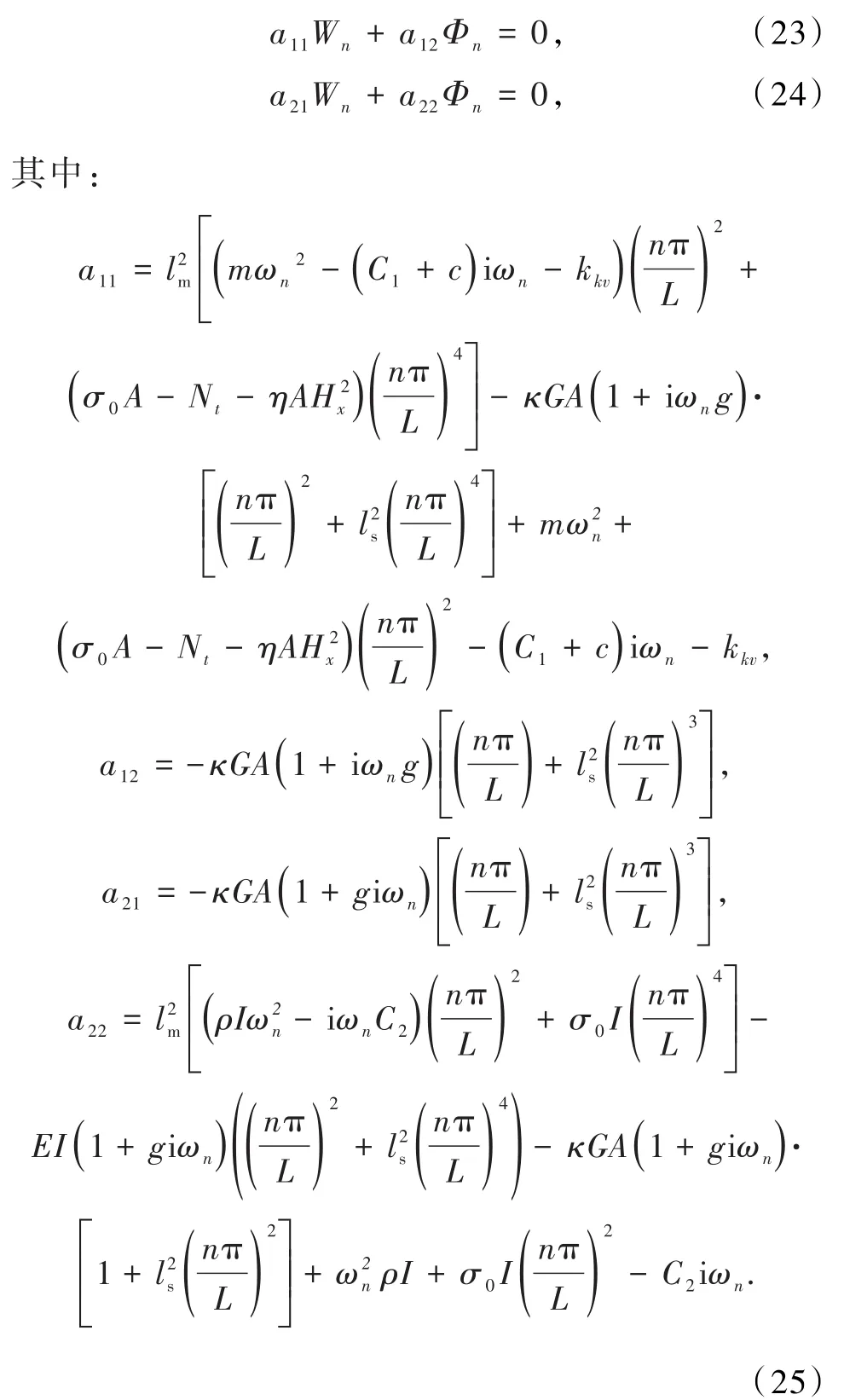
将（23）和（24）写成矩阵形式为

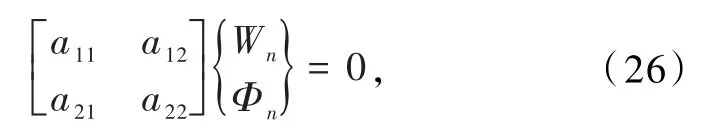
式中aij是包含ωn和其他参数的多项式，考虑Wn和Φn在方程组中有非平凡解的条件为系数矩阵行列式等于0，即可得到振动频率（ωn）与其他系统参数的关系.

2 数值结果分析

2.1 模型参数

考虑单壁碳纳米管，本文参数设置为E=1 TPa，ν=0.28，碳纳米管的直径d=1.1nm，L=10d，壁厚t=0.342 nm，ρ=2.24×103kg/m3，κ=0.563，ls/d=1/6，C1=8.99 × 10-7(kg·N/m3)1/2，C2=5.27 × 10-26(kg·m·N)1/2［18-19］，对置于 Kelvin-Voigt粘弹性基础、在力-热-磁耦合场中且有阻尼的不同工况进行分析.其中αx=-1.6 × 10-6K-1［20］，η=4π × 10-7H/m［21］，kkv=380 MPa，c=4.50 × 10-7(kg·N/m3)1/2［22］.

2.2 小尺度效应对频率的影响

研究显示，非局部模型在微观尺度上随着非局部系数的变化对振动频率有着很大的影响，在有阻尼条件下，频率在力-热-磁耦合场中随固有模态阶数变化情况如图2所示.计算选取参数为T=40 K，σ0=4.84×108Pa，Hx=107A/m，g=7.10×10-14(kg·m/N)1/2.在前10阶范围内，频率随着固有模态阶数升高而增大，不同的非局部系数lm=[0.1，0.2，0.3]×L变化结果表明，lm的增大对频率会有抑制作用.不同固有模态阶数下，频率随非局部系数的变化如图3所示.由图可知，频率随非局部参数的增大会非线性减小，且不同阶的振动频率关于lm变化的程度不同，在第一阶固有频率时变化较小.lm为小尺度效应的参数，即小尺度效应的影响在模态阶数越高的时候越明显.

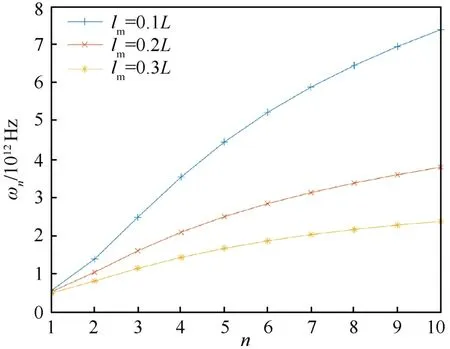
图2 前10阶固有频率在非局部系数影响下的变化

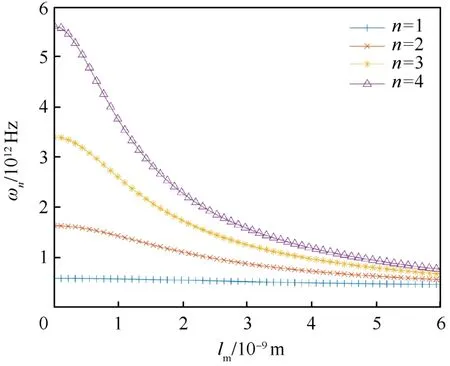
图3 不同固有模态阶数下频率随非局部系数的变化

2.3 力-热-磁耦合场参数对频率的影响

力-热-磁耦合场参数对频率的变化如图4～6所示.计算中涉及的参数为lm=0.1L，g=7.10×10-14(kg·m/N)1/2，T=40 K，Hx=107A/m，σ0=4.84× 108Pa.结果表明，频率随着磁场强度增大而增大，随着轴向初始应力增大而减小，而温度增长，频率则会略微减小.对耦合情况进行分析，在不考虑温度对弹性模量的影响情况下，温度升高对于轴向应力和磁场强度耦合作用并不明显（图5和6）.而对于磁场强度和轴向初始应力的耦合情况（图4），当磁场强度高时，轴向初始应力对于频率的影响较于低磁场强度小；初始应力大时，磁场强度的影响会更大.对于磁场和轴向初始应力的耦合关系，考虑是磁场引起的洛伦兹力与轴向初始应力叠加引起.

图4 轴向初始应力和磁场强度对第一阶固有频率的影响

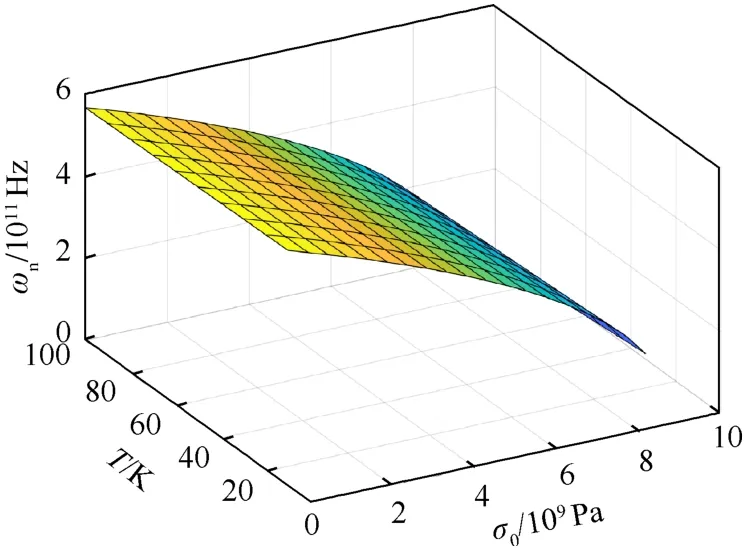
图5 轴向初始应力和温度对第一阶固有频率的影响

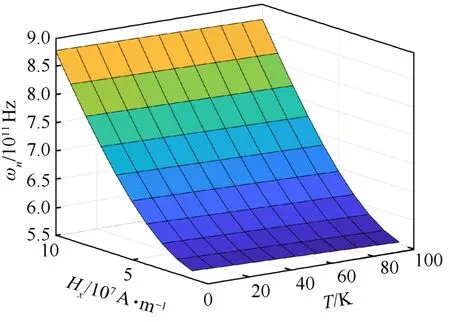
图6 磁场强度和温度对第一阶固有频率的影响

2.4 初始轴向应力对频率的影响

轴向初始应力的方向以及轴向初始应力和非局部系数的关系如图7所示.计算选取参数为T=40 K，Hx=107A/m，，σ0=4.84×108Pa.分析可知，初始轴向应力以0值为分界线，其中左边承受拉应力，右边承受压应力.结果表明：随着压应力的增大频率逐渐减小；相反，随着拉应力增大频率逐渐增大，即轴向压应力有抑制振动频率的作用，而小尺度效应对频率的影响随着压应力的增大而增大.考虑碳纳米管失稳，按照经典屈曲理论，计算得失稳的最小临界应力为1.911×1010Pa，远大于文中轴向应力，且由文献可知［23］，当碳纳米管达到临界屈曲应力时，其振动频率为0，而本文关于初始轴向应力数值计算结果中频率还未降到0，所以，综合考虑碳纳米管还未达到屈曲失稳的状态.

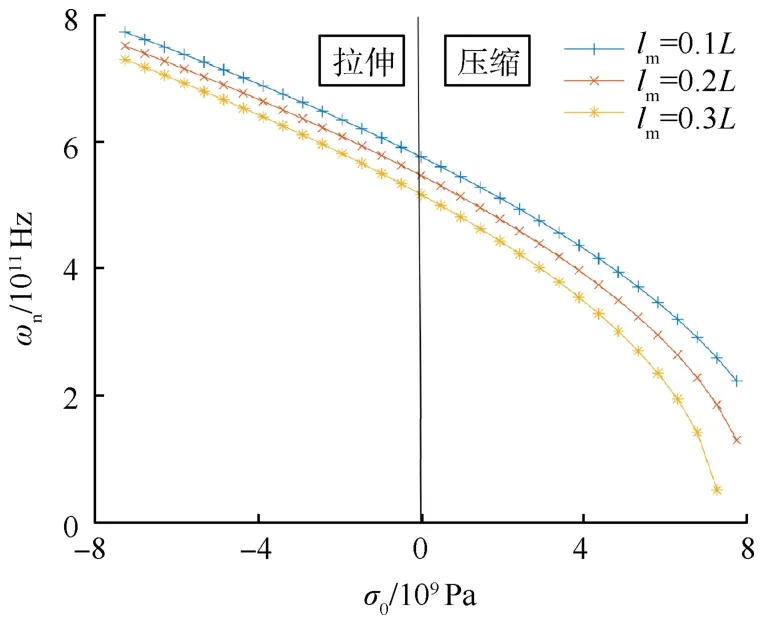
图7 轴向初始应力和非局部系数对第一阶固有频率的影响

2.5 粘弹性阻尼系数对频率的影响

分析粘弹性阻尼与非局部系数的关系如图8所示.与非局部系数相比，粘弹性阻尼系数对频率影响非常小，且随着非局部系数变化不会改变粘弹性阻尼系数对频率的影响.

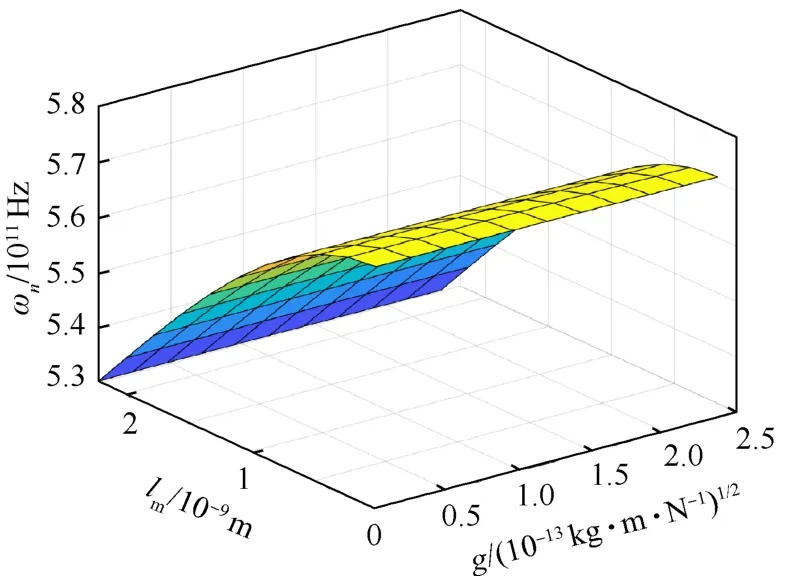
图8 阻尼系数和非局部系数对第一阶固有频率的影响

3 结 论

本文应用统一应力应变梯度弹性模型，考虑粘弹性基础和外部阻尼，推导了Timoshenko碳纳米梁在力-热-磁耦合场中的振动方程.分析了粘弹性阻尼、小尺度效应和力-热-磁耦合场参数对碳纳米管振动频率的影响，可以得到以下结论：

（1）小尺度效应对振动频率的影响较大，较大的非局部系数对频率有抑制作用，且这种作用对于越高阶的振动频率越明显.

（2）不考虑温度对弹性模量的影响，温度升高频率会降低，但是相对于其他变量的影响很小，频率随着磁场强度增大而增大，随着轴向应力增大而减小.磁场强度增大会减小轴向应力对频率的影响，而轴向应力增大则会放大磁场强度的影响.

（3）对于初始轴向应力，轴向压应力有抑制振动频率的作用.非局部系数的增大会使轴向应力对频率影响增大，小尺度效应对频率的影响随着压应力的增大而增大.

（4）在文中取值范围内，粘弹性阻尼系数对振动频率的影响不明显.