实施微探究教学 把问题教学落实于课堂*
——一道课本习题的微探究教学与推广应用
2021-12-30孙西洋
孙西洋
(江苏省南京市第二十中学 210036)
1 问题的提出
在苏教版高中数学必修2第二章“平面解析几何初步”P117有习题11:
已知圆C:x2+y2=r2,求证:经过圆C上一点M(x0,y0)的切线l方程是x0x+y0y=r2.
习题12:已知圆O:x2+y2=r2,直线l:x0x+y0y=r2,分别根据下列条件,判断直线l与圆O的位置关系:(1)点M(x0,y0)在圆O上;(2)点M(x0,y0)在圆O外;(3)点M(x0,y0)在O内.
2 习题的微探究教学
“微探究”是根据教学内容,围绕某个小知识点或某一问题,在教师的组织、引导下,让学生运用自我探究与合作交流的方式进行学习.在十年的课改过程中,探究教学的理念虽然已经深得人心,探究式教学的方式已经在数学教育界形成了广泛的共识.但真正做到在课堂教学中的常态化却举步为艰,教学的现状令人担忧.而微探究教学作为探究教学的一种,为数学课堂探究教学找到了一种有效的实施途径.下面笔者结合自己的教学实践,谈谈经过圆x2+y2=r2上一点M(x0,y0)作圆的切线等相关问题的微探究教学及其应用过程.
师:如何求经过圆C:x2+y2=r2上一点M(x0,y0)所作的圆的切线l的方程?

师:生1对圆的切线的概念掌握得比较好.请同学们交流一下,看看生1的解题过程中是否有需要完善的地方?
生2:如果x0=0,此时直线OM的斜率k′不存在,切线的斜率为0,切线的方程是l:y=y0.如果y0=0,直线OM的斜率为0,切线的斜率不存在,这时切线方程为x=x0;在以上两种情况下,直线l的方程都满足x0x+y0y=r2,所以切线的方程是x0x+y0y=r2.
师:生2思维缜密,考虑周到,非常好.这里根据直线的位置情况对直线的斜率情况进行了分类讨论,分类讨论是同学们高中阶段需要面对的重要策略与方法,需要认真领会,灵活运用. 同学们是否有不需要分类讨论就能得到切线方程的方法?

师:生3利用向量的垂直关系求出切线的方程,避开了分类谈论,很好. 是否还有其他方法?
生4:我想利用勾股定理来证明,不知道是否可行?
师:我们请生4谈谈他的想法.
生4:设P(x,y)是切线上任意一点,则OP2=OM2+MP2,代入坐标得
化简得切线的方程是l:x0x+y0y=r2.
师:生4的想法很好,与生3的解法类似,避开了分类讨论.那如果圆C的方程为C:(x-m)2+(y-n)2=r2,点M(x0,y0)在圆C上,那么切线l的方程如何求解?切线方程应该是什么?
生5:我想切线的方程应该是(x0-m)(x-m)+(y0-n)(y-n)=r2.
师:请生5与大家分享一下自己的思考过程.


师:生5的想法与做法都很好.请同学们再思考一下,如果点M(x0,y0)在圆C:x2+y2=r2外部,那么直线x0x+y0y=r2与圆C的位置关系如何?如何判定?

师:如果点M(x0,y0)在圆C的内部(x0,y0不同时为零),直线x0x+y0y=r2与圆C:x2+y2=r2的位置关系怎样?
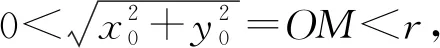
师:生7回答得很精当.同学们知道,在考查直线与圆的位置关系时,首选的做法就是利用圆心到直线的距离d与半径的大小关系来衡量它们的位置关系.当d>r时直线与圆相离;当d=r时直线与圆相切;当d 生8:根据上述分析,我们有如下结论: 当点M在圆C上时,直线l与圆相切,x0x+y0y=r2是经过点M的圆的切线的方程; 当点M在圆C外部时,直线l与圆相交; 当点M在圆C内部时,直线l与圆C相离. 师:如果点M(x0,y0)在C:x2+y2=r2外,直线x0x+y0y=r2除了与圆C相交,还具有什么样的性质? 生9:既然这条直线与圆相交,而且直线又与点M相关联,所以直线应该是经过点M作圆的两条切线,两切点所在的直线方程. 师:很好!我们把这条直线叫做切点弦所在的直线,那我们应该如何求出切点弦所在的直线的方程呢? 生10:用前面求切线方程相对应的方法求解,运用“设而不求”思想. 师:你愿意将你的思考与同学们分享一下吗? 生10:经过点M作圆的切线有两条,设切点分别是A(x1,y1),B(x2,y2),则经过点A的切线为x1x+y1y=r2,因为切线经过点M,所以x0x1+y0y1=r2;经过点B的切线为x2x+y2y=r2,因为切线经过点M,所以x2x0+y2y0=r2,于是直线x0x+y0y=r2经过点A,B两点,由于两点确定一条直线,所以直线AB的方程为x0x+y0y=r2. 师:生10真聪敏,利用“设而不求”思想求出了切点弦所在的直线方程.同学们还有其它思考吗? 生11:我的想法与生10的解法不同,请老师与同学们看看我的解法是否可行? 师:那我们就一起来欣赏一下学生11的想法,等一会请同学们给出评价. 生11:以OM为直径的圆的方程是x(x-x0)+y(y-y0)=0,即x2+y2-x0x-y0y=0, 所以圆x2+y2-r2=0与圆x2+y2-x0x-y0y=0相交的交线AB的方程是x0x+y0y=r2,所以x0x+y0y=r2就是切点弦所在的直线AB的方程. 师:生11利用两个圆C1:x2+y2+d1x+e1y+f1=0,C:x2+y2+d2x+e2y+f2=0相交,得它们的交线所在直线的方程是(d1-d2)x+(e1-e2)y+f1-f2=0正确吗?哪位同学给予评价? 师:同学们交流一下,看看生11的做法是否正确? 同学们思考一下,是否还有其它解法? 师:同学12的解法也是利用两个相交圆的方程相减得到切点弦所在的直线方程,虽然他们寻找的两个圆不同,但是却殊途同归,非常好!同学们还能将这个结论进行推广吗? 生13:如果点M(x0,y0)在圆C:(x-m)2+(y-n)2=r2③外,那么方程(x0-m)(x-m)+(y0-n)(y-n)=r2就是经过点M作圆的切线的切点弦所在的直线方程. 师:这个推广的结论对吗?谁会证明这个结论?谁能给予解释? 生14:结论推广正确,我是这样来证明的: 以线段MC为直径的圆的方程是:(x-m)(x-x0)+(y-n)(y-y0)=0, 即(x-m)[(x-m)+(m-x0)]+(y-n)[(y-n)+(n-y0)]=0, 即(x-m)2+(x-m)(m-x0)+(y-n)2+(y-n)(n-y0)=0④, ④-③得两个圆的公共弦所在的直线的方程是(x0-m)(x-m)+(y0-n)(y-n)=r2. 师:生14很善于思考,回答得非常好.前面生10提出了“设而不求”思想.“设而不求”是我们研究解析几何问题时经常用的一种重要策略,哪位同学能谈一谈什么叫“设而不求”思想? 生10:“设而不求”就是在解决数学问题时,先设定一些未知数(未知的点的坐标),然后把它们当成已知数(已知点),然后根据题设本身各个量之间的制约关系,建立相应的数学模型,但是不需要求出未知数(点的坐标),而根据题目本身的特点,将未知数消去或代换掉,从而使问题的解决变得简捷、明快.由于在数学尤其是解析几何的学习中,经常使用,为了便于使用,我把它叫做“设而不求”法. 师:很好,生10是一位有心人,在平时的学习中,不仅注重解决数学问题,同时也关注学习方法,难能可贵!还有其它解法吗? 生15:可以利用前面求经过圆O:x2+y2=r2外一点M(x0,y0)作圆O切线的切点弦类似的各种方法求出切点弦所在的直线方程. 师:生15说得对,前面相应的方法都可以求出直线的方程.请同学思考一下:“经过圆C:x2+y2+dx+ey+f=0外一点M(x0,y0)作圆C的两条切线,切点弦所在的直线方程是什么?” 如经过点(-1,-3)作圆:x2+y2-4x-6y+12=0的两条切线的切点弦所在的直线的方程是-x-3y-2(x-1)-3(y-3)+12=0,即3x+6y-23=0. 师:刚才我们知道如果点M(x0,y0)在圆x2+y2=r2内,那么直线x0x+y0y=r2是与圆O相离的直线.其几何意义是什么? 生17:我们的结论是:经过点M任作圆O的弦,弦的端点处的切线交点的轨迹. 证明如下:设AB是经过点M的任意一条弦,设A(x1,y1),B(x2,y2),对应交点P(m,n), 则经过A的切线的方程是:x1x+y1y=r2,因为该直线经过点P,所以mx1+ny1=r2. 同理可得mx2+ny2=r2,所以直线mx+ny=r2是经过点A,B的直线的方程,而直线AB经过点M,所以x0m+y0n=r2,所以点P的轨迹方程是x0x+y0y=r2. 师:生17用设而不求思想分析了直线x0x+y0y=r2的几何意义. 问题教学指的是以问题贯穿课堂教学全过程,让学生在设问、释问的过程中激发学习的欲望和动机,逐渐养成良好的学习习惯,在教学实践中不断优化教学方法,提高学生的学习能力.问题教学改变了传统教学模式和教学方法,充分尊重学生的主体地位,能够有效激发学生的学习积极性和主动性,提高课堂教学的效果. 问题是思维的源泉,数学作为一门基础性学科,数学教学最终的目标是通过发现问题、解决问题,完成数学教学的目标和任务,促进学生的全面发展.在新课程理念下,对在数学教学中或者学生数学学习中面临的一些难点、重点问题,教师带领学生进行微探究教学,能有效改进高中数学课堂教学模式,优化课堂教学结构,构建高效课堂,促使学生学习能力的提升与学习方法的变革,促进学生自主学习、合作学习. 在数学教学过程中,教师以问题组织课堂,教师的课堂教学,不仅是传授知识的过程,更重要的是以一种独特的思维艺术将教学内容与学生的兴趣结合起来,为学生创造一个独立思考的空间.问题教学为高中数学教学创造了一个具体的背景,营造了良好的问题情境,激发学生的问题意识,以增强学生的求知欲望. 数学教学最重要的是数学思维的培养.从本质上说,数学思维是一种趋于理性、抽象性的思维方式,是在长期的数学学习中逐渐形成的.问题是思维发展的强大的动力,教师为学生提供了合适的思考方向,增强了学生的解决问题、思考问题的欲望,在这种循环解决问题的过程中,能够加深学生对数学知识的理解. 在问题教学过程中,教师还应重视问题设置的方式,努力构建高效课堂.在问题设置时,需注意以下三个方面: 新奇性 教师在问题设置时,应注意问题的独特性与新颖性,以好奇心来调动学生的学习兴趣,让学生融入到课堂教学中. 层次性 在问题设置时,教师应根据学生的学习情况,由易到难,由简单到复杂,层层推进,在基础知识积累到一定程度后,再解决更复杂的问题. 情境性 在课堂教学中,教师应创设与问题相应的情境,通过变式训练逐步引申以达成最终目标,让学生在身临其境中学习,在自主探究与合作交流中实现自主发展,丰富学生想象力,以吸引学生的注意力. 在教学过程中,教师应该认识到,培养学生的问题意识非常重要.学生在学习过程中,随着知识的积累,求知欲和好奇心会逐渐降低,学习的兴趣也不断减弱.因此,教师应适时采取措施,以支持和引导学生的积极思考,为学生创设必要的问题情境.同时,教师应发扬教学民主,鼓励学生提出问题,不管问题的难易与否,教师都应该进行耐心解答,以增强学生的自信心.在问题深入方面,教师应多进行引导,让学生能够深入思考,使学生从问题表面深入到问题的本质上来.在问题教学过程中,教师应容忍错误,多加鼓励.数学学科自身的抽象性,对于学生来说也有一定的难度,教师如果不适当引导,会导致学生的胆怯心理,不利于数学教学活动的顺利开展.因此,教师应不断鼓励学生,让学生把问题提出来,在解决问题过程中提高数学学习的效果.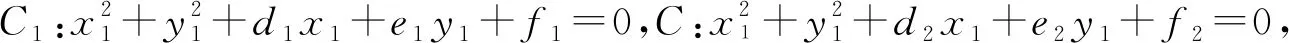

3 教学反思
