煤矿立井井筒双圈管冻结不同地层冻结效果研究

刘 稳 倪 贤

(安徽理工大学土木建筑学院，安徽 淮南 232001)

1 概述

近年来，我国对煤矿的开采逐步向深地层方向发展，而多圈管冻结是深厚地层井筒建设的主要施工方法[1，2]。随着开挖深度的增加，冻结法施工过程中的发展规律日趋复杂。为及时准确地判断冻结壁发展状况、科学地指导施工,基于煤矿立井井筒双圈管冻结工况进行数值模拟具有重要意义[3，4]。

2 工程概况

2.1 冻结方式及深度设计

淮北某矿副井冻结设计采用主排孔+辅助孔冻结方式，井筒深度为440 m，冻结段井壁壁座底部深340 m，冻结深度为350 m。

2.2 冻结壁设计

副井净直径为5.5 m，最大开挖荒径为8.506 m，控制层位为松散层底部-262.4 m粘土层(绝对标高)，控制层冻结壁平均温度为-12 ℃，冻结壁设计厚度为5 m。

2.3 冻结孔设计

冻结孔采用主排孔+辅助孔冻结方式，参数如表1所示。

表1 冻结孔设计参数

2.4 测温孔及水文孔设计

为了准确掌握冻结温度场变化情况，设计3个测温孔，分别布置在主、界面上。温度测点在各孔内沿垂直方向每隔20 m～50 m左右布置一个测点，或按特殊地层测点布置考虑，以监测不同方位、不同深度地层的冻结温度。具体位置和深度视施工情况布置。75 m层位以上各控制层位分别布置3个测温孔，75 m层位以下各个控制层位分别布置两个测温孔。测温管采用φ108×4.5 mm的20号低碳无缝钢管，外箍焊接连接，焊接质量同冻结管，管内不允许灌水试压，但不得渗漏水。

井筒内布置2个水文孔，单层报导，浅孔32 m报导第一含水层的交圈情况，一含埋深30.75 m。含水砂层厚18.50 m。深孔183 m报导第三含水层的交圈情况，三含埋深189.30 m，含水层厚度51.60 m。

水文管设计采用φ140×5 mm的20号低碳无缝钢管，内箍焊接连接。花管水位报导段采用φ140×6 mm的20号低碳无缝钢管加工定制。

3 二维冻结温度场数学模型

二维土体冻结温度场是一个具有相变、有内热源、冻结锋面移动且边界条件复杂的瞬态导热问题。由于煤矿立井冻结尺寸纵向比横向大得多，且热传导现象基本发生在平面内，所以煤矿立井冻结温度场可以简化为二维平面热传导温度场问题，温度场控制方程为：

(1)

在冻结锋面处：

(2)

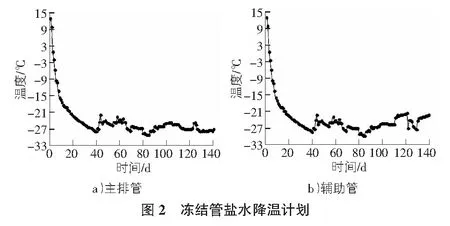
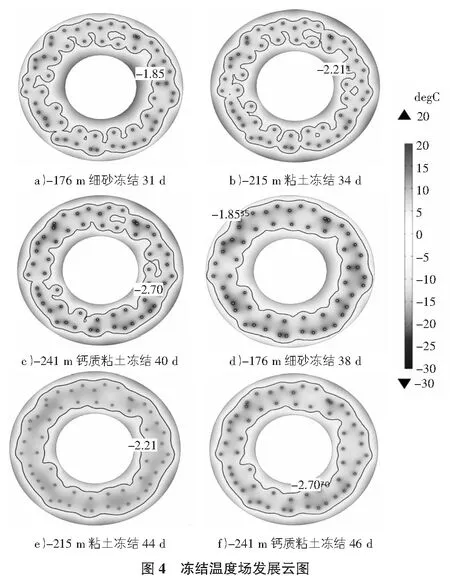
其中，Tn为温度分布，℃；n为岩土体状态，n=1为未冻土，n=2为冻土；Cn为比热容，kJ/(m3·℃)；kn为土体的导热系数，W/(m·℃)；t为时间，s；r为圆柱坐标，以井筒中点为坐标原点，m；ξN为冻结锋面在N区域内的坐标，当N=1时，0<ξN

冻结开始前，土体内具有单一的初始温度：

T=T0|t=0

(3)

其中，T0为土体的初始温度，℃。

在无限远处，土体不受冻结影响，始终保持初始温度不变：

T=T0|r=∞

(4)

冻结锋面处，土体温度为土体的冻结温度：

T=Td|r=ξN

(5)

其中，Td为土体的冻结温度，℃。

模型中，直接将盐水温度作为温度荷载加在冻结管外壁上：

T=Tc|r=Rp

(6)

其中，Tc为盐水温度;Rp为冻结管半径，该处圆柱坐标为以各冻结管中心为原点的局部坐标系。

4 数值计算模型

4.1 基本假设

1)同一层位的未冻土与冻土均为向同性材料。

2)不考虑水分迁移的影响。

3)不考虑模型与外界的热量交换，假定模型的外边界为绝热边界。

4)将现场相应的盐水去路温度直接加在对应的冻结孔边界上作为温度荷载。

4.2 数值计算模型及参数

选取该矿副井-176 m细砂层位、-215 m粘土层位以及-241 m钙质粘土层位作为数值计算模型，三层位冻结孔与测温孔设计孔位如图1所示。取半径为20 m的圆形区域，计算模型中冻结孔与测温孔位置为考虑钻孔偏斜情况下的实际成孔位置，为了增加模型的计算精度且减少计算时间，模型中在靠近冻结管附近的区域由于温度梯度较大，对于该区域网格进行加密，对于远离冻结管温度变化梯度不大的区域采用粗化网格，网格采用自由剖分三角形网格。土体的热物理参数如表2所示。

表2 土体热物理参数

埋深m土性密度kg/m3导热系数W/(m·K)比热容J/(kg·K)未冻结冻结未冻结冻结相变潜热kJ/kg冰点℃-176细砂1 9351.512.251 1881 02735.7-1.85-215粘土1 9411.422.081 2501 36037.2-2.21-241钙质粘土1 9501.211.881 0531 34532.8-2.70

4.3 初始温度及边界条件

根据现场地温测试结果，-176 m细砂层位、-215 m粘土层位以及-241 m钙质粘土层位的土体冻结前初始温度分别为21.6 ℃,22.5 ℃和23 ℃，主排孔和辅助孔的温度取现场实测的盐水去路温度，如图2所示。

5 数值计算结果与分析

5.1 数值计算与实测结果对比

为了验证数值模拟的合理性，分别将-176 m细砂层位、-215 m粘土层位以及-241 m钙质粘土层位的C1与C2测点的模拟数据与实测数据进行对比。如图3所示，三个层位中的C1和C2测点的模拟实测温度相差均小于1 ℃，说明数值计算模型以及参数选取合理，数值计算能够较好的反映现场的实际冻结情况。

5.2 温度场时空分析

5.2.1冻结壁交圈过程

如图4所示，冻结壁交圈之前，冻土以冻结管为中心向四周扩展，冻结壁交圈以后，冻结壁以环形向两侧扩展。由于外圈主排孔布置较密，外圈孔之间的孔距较小，冻结过程中外圈孔处的冻结壁先交圈，细砂层位、粘土层位以及钙质粘土层位外圈管冻结壁交圈时间分别为31 d，34 d以及40 d。而三个层位的冻结壁完全交圈的冻结时间分别为38 d，44 d以及46 d。并且可以看出，冻结壁在完全交圈以后，细砂层位的冻结壁平均温度明显低于粘土层以及钙质粘土层。因此，从冻结壁交圈情况来看，冻结效率为细砂>粘土>钙质粘土。

5.2.2冻结壁厚度发展情况

如图5所示，同一时刻，细砂层位的冻结壁厚度明显大于粘土层位与钙质粘土层位，并且随着冻结不断进行，差距越来越大。同一时刻粘土层位冻结壁厚度要略大于钙质粘土层位。冻结至50 d时，细砂层位、粘土层位以及钙质粘土层位的冻结壁厚度分别为3.72 m,3.38 m和3.3 m。冻结至140 d时，细砂层位、粘土层位以及钙质粘土层位的冻结壁厚度分别为6.69 m，5.84 m和5.7 m，因此可以看出冻结壁交圈以后，细砂、粘土以及钙质粘土层位的冻结壁平均扩展速率为3.30 cm/d，2.73 cm/d和2.67 cm/d。因此，从冻结壁扩展速率来看，冻结效率为细砂>粘土>钙质粘土。不同层位的冻结壁厚度在冻结过程中的变化规律基本一致，都呈指数函数形式变化。利用origin对三种不同地层的冻结壁厚度随时间变化情况进行拟合，可以得出冻结壁厚度随时间的变化曲线分别为：

E1=2.898 72lnt-7.676 56

(7)

E2=2.457 93lnt-6.305 27

(8)

E3=2.349 98lnt-5.948 08

(9)

其中，E1,E2和E3分别为细砂、粘土与钙质粘土的冻结壁厚度，m；t为冻结时间，d；其中式(7)～式(9)的决定性系数分别为99.847%,99.743%和99.795%。

5.2.3冻结壁平均温度变化情况

如图6所示，不同层位冻结壁的平均温度随时间的变

化规律基本一致。冻结壁在交圈以后，冻结壁平均温度随冻结时间迅速降低，冻结相同时间，钙质粘土层位的冻结壁平均温度最低，粘土层位次之，细砂层位最高，基本上表现为冻结壁交圈以后，冻结相同的时间时，土层的冻结温度越低，相应的冻结壁平均温度越低。从冻结孔降温曲线来看，冻结86 d时，主排孔和辅助孔的盐水温度均开始升温，尤其是辅助孔的盐水温度，到冻结120 d时，辅助孔盐水温度较冻结90 d时升高将近5 ℃，由此造成了冻结壁的平均温度在冻结90 d以后开始升高，不同层位冻结120 d时较各自层位冻结90 d时的冻结壁平均温度升高了1 ℃以上，因此可以看出冻结盐水温度对于冻结壁平均温度影响较大。

6 结论

本文以淮北某矿副井井筒冻结工程为实例，选取冻结孔实际成孔相近、土性不同的三个地层，采用有限元软件COMSOL Multiphysics对-176 m细砂、-215 m粘土与-241 m 钙质粘土层位三个地层进行温度场计算分析，得出以下规律与结论：

1)考虑冻结孔及测温孔的实际成孔位置，以现场测温孔实测数据为基础，建立二维双圈管立井井筒冻结温度场数值计算模型，对现场的温度场进行计算。计算结果表明，两个地层的测温孔数值计算温度与现场实测温度吻合程度较高，说明运用有限元计算二维双圈管冻结温度场是可行的。

2)基于数值计算结果，对细砂层位、粘土层位以及钙质粘土层位的温度场进行计算，预测冻结温度场的发展与分布规律。结果表明：相同的冻结条件下，细砂层位先交圈、粘土层位次之、钙质粘土层位最后交圈；冻结壁扩展速率方面，细砂层位冻结壁扩展最快，粘土层位次之，钙质粘土层位冻结壁厚度扩展速率最慢；冻结壁交圈以后，冻结相同时间，钙质粘土层平均温度最低，粘土层位次之，细砂层位最高。