压缩机入口管道疲劳断裂分析
2021-12-30王高杰李慧芳卢敬田王传志钱才富
王高杰 李慧芳 卢敬田 王传志 钱才富
(1.北京化工大学机电工程学院;2.中国石化燕山分公司合成树脂厂;3.北京燕华工程建设有限公司)
往复式压缩机在石油化工行业应用十分广泛。由于其间歇式的吸排气工作方式会使管道内气体流速与压力发生周期性变化。在管道系统中产生的压力脉动会在弯头、三通或阀门等截面处产生激振力引起管道振动。过大的管道振动会导致管道系统疲劳失效,对安全生产有着巨大威胁。
管路振动的原因有两种,一种是由于运动机构的动力平衡性差或基础设计不当而引起的管路振动,另一种是由于气流脉动引起的管路振动[1]。Liang Z等针对往复式压缩机进口管道发生异常振动的问题,对管道进行模态分析、共振管长度计算和压力脉动测量,研究发现进口管道发生了声共振是引起异常振动的关键因素[2]。牛福春和顾海明计算了压缩机管系的气柱固有频率、结构固有频率和管内的气流压力不均匀度,分析表明管系的水平管段刚度较低即使激振力较小也会激起较大的管道振动[3]。韩文龙等根据计算流体力学CFD方法建立了管道系统流体动力学模型,与实验结果对比发现标准k-ε湍流模型更加合理,证明利用CFD技术模拟管道系统气流脉动是切实可行的[4]。郝春哲等运用管路气柱分析软件Bently PLUS对某往复式压缩机管路系统的气柱进行声学模拟,应用管路应力分析软件CAESARⅡ对管路进行静态分析和疲劳应力分析,结果表明管道发生了气柱共振和机械共振,并提出了改进方案[5]。郭文涛和肖明鑫利用DIGMO和CAESARⅡ分析软件对压缩机管线的振动进行综合分析,并通过实践验证了该技术可行且成熟可靠[6]。熊怡君采用网络传递矩阵法,建立了大型往复式压缩机管道系统气流脉动的网络计算模型,并开发了Matlab程序代码,计算气柱固有频率和气体压力脉动[7]。
笔者针对某往复式压缩机入口管道的断裂失效,进行断裂分析、材料实验、静力分析、模态分析、谐响应分析、动力分析和疲劳裂纹扩展分析,还针对不同刚性的管卡支撑,计算疲劳裂纹扩展寿命。
1 往复式压缩机入口管道断裂失效分析
压缩机气体入口管道位于二次二段压缩气缸之前,该管道前面连接有缓冲罐。管道由Z形管道和两个法兰组成,其中管道与法兰为螺纹连接。管道安全运行多年后,巡检发现弯管与缓冲罐连接端的管道外壁近螺纹根部处产生裂纹,造成管道的泄漏失效。
1.1 管道材料金相分析
材料的化学成分检验结果显示弯管材料成分符合设计材料要求,力学性能检测结果显示弯管材料满足设计对材料的强度要求,同时弯管材料的冲击韧性指标也能满足该牌号的冲击韧性要求。金相检验结果表明材料为调质状态,符合材料设计要求,晶粒度为7级,说明材料淬火温度正常,与材料的力学性能结果相吻合;非金属夹杂物的评定显示该管材非金属夹杂物中氧化物偏多,单颗粒球状物评级达2级,且数量多,但是基于当时的冶炼与检测技术,对非金属夹杂物没有明确要求,不能判定材料不合格。
1.2 断口分析
宏观观察发现断口上有贝纹状花样,贝纹带是装置开/停车时应力受到干扰,疲劳裂纹所留下的痕迹。贝纹推进从疲劳源开始,凸向即为裂纹扩张方向,未发现瞬断区,说明裂纹贯穿时材料所承受的静载荷仍没有超过材料的屈服极限,也就是说内压不足以使管子发生爆裂。从贝纹凹凸方向判断,裂纹从外壁发生,向内壁扩展。在放大100倍显微镜下观察裂纹形貌为波浪式向内壁推进,符合循环应力作用于管线的特征。
非金属夹杂物的检验表明该管段部分非金属夹杂物中的氧化物类夹杂物较多,而且存在很多单颗粒球状物,Ds评级为2.0级,夹杂物在裂纹扩展中起到了加速和分支的作用。由于夹杂物的存在造成基体的不连续性,而且极易在夹杂物周围形成空洞、位错等缺陷的集聚,从而加速裂纹发展或改变裂纹方向。
电镜观察发现断面上有疲劳辉纹,疲劳断面在微观范围内由许多大小不同的,高低不同的小断块组成,每个断块上的疲劳辉纹连续且平行,但相邻小断块上的疲劳辉纹不连续、不平行。电镜观察未见到韧窝、轮胎压痕等低周疲劳特征。
由材料取样分析和断口检测分析可初步得到以下结论:
a.由于弯管段与缓冲罐为刚性连接,这种结构螺纹尖端接触面应力集中,造成裂纹发生在弯管与缓冲罐连接的固定端,裂纹起源于外壁近螺纹根部;
b.裂纹发展符合高周疲劳裂纹扩展特征;
c.裂纹起源处存在Ds单颗粒球状类非金属夹杂物;
d.断面未见瞬断区,裂纹自萌生后至断裂处于裂纹稳定扩展段;
e.疲劳应力来源于管道内介质的温度、压力及流动等波动。
2 40CrNiMoA的拉伸实验和疲劳裂纹扩展实验
2.1 弹性模量的测定实验
按照GB/T 228.1—2010《室温试验方法》的规定选取试样的形状和尺寸。本实验所用试样为机加工的矩形横截面比例试样,按照附录D确定试样尺寸,具体如图1所示,其中试样厚度a0=4 mm,平行长度段的宽度b0=15 mm,过渡弧半径R=12 mm,比例系数k=5.65,平行长度Lc=70 mm,试样编号P8。
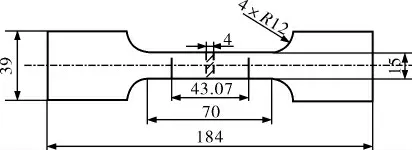
图1 机加工的矩形横截面比例试样尺寸
拉伸实验得到了4组试样的应力-应变曲线,4组试样的应力-应变曲线的趋势相同,文中只列出试样1的应力-应变曲线(图2)。对4组试样线弹性阶段的应力-应变曲线进行线性拟合(图3),拟合结果为弹性模量201.615 GPa,残差平方和306.18,调整后R平方0.999 06。
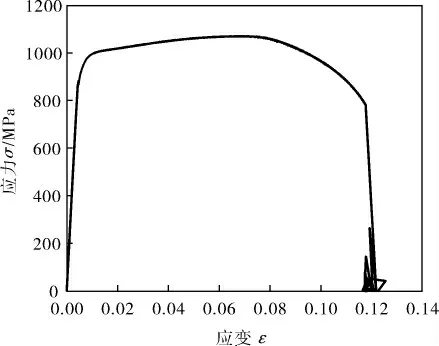
图2 试样1应力-应变曲线
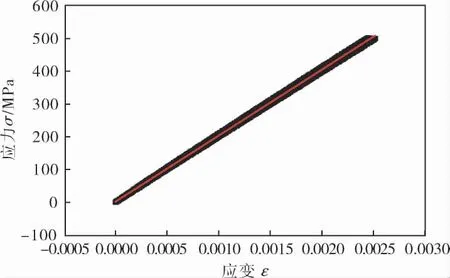
图3 拉抻试样线弹性阶段应力-变应曲线
2.2 材料的Paris常数C和m测定实验
材料的Paris常数C和m的测定实验根据GB/T 6398—2000《金属材料疲劳裂纹扩展速率试验方法》选用标准中心裂纹拉伸M(T)试样,按照标准选取试样宽度W、试样厚度B和试样长度L,不包括加载孔的试样中间部分尺寸如图4所示。疲劳试验参数为:试验循环最大力PMAX=40 kN,循环最小力PMIN=4 kN,力值比为0.1。
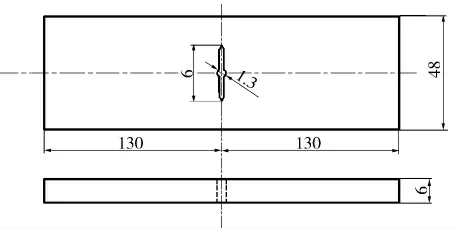
图4 标准中心裂纹拉伸M(T)试样尺寸
材料的Paris常数C和m测定实验共获取5组实验数据。实验过程中,裂纹向前扩展0.5 mm时记录一次疲劳循环次数和裂尖位置,试件1的裂纹扩展路径垂直于加载方向,显然这是Ⅰ型裂纹。图5为测得的单边裂纹长度a与对应的疲劳循环次数N之间的关系曲线。
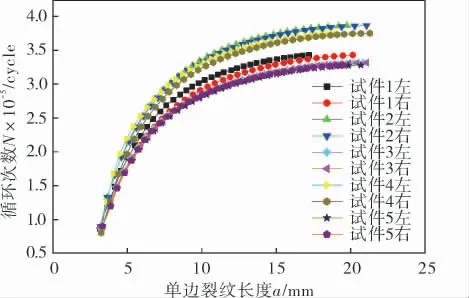
图5 单边裂纹扩展a-N曲线
2.2.1 应力强度因子范围计算
依据实验测得的裂尖位置,采用有限元法可以计算得到裂纹尖端的应力强度因子范围ΔK,所用单元为高阶二维八节点平面单元PLANE183。结果发现有限元计算得到的应力强度因子范围ΔK与GB/T 6398—2000标准推荐的应力强度因子范围计算得到的ΔK相吻合。
2.2.2 裂纹扩展速率计算
GB/T 6398—2000附录A中推荐了七点递增多项式法求解d a/d N,笔者用Matlab编写七点递增多项式数据处理程序计算裂纹扩展速率。
2.2.3 Paris曲线绘制
图6为计算所得的应力强度因子范围ΔK和对应的裂纹扩展速率d a/d N之间的关系,图7为双对数坐标系下的结果。

图6 疲劳裂纹扩展速率d a/d N与ΔK的关系
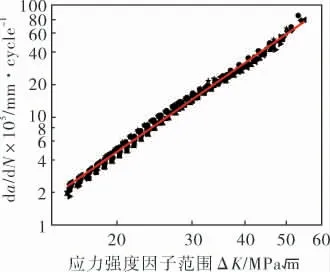
图7 双对数坐标中疲劳裂纹扩展速率d a/d N与ΔK的关系
采用Pairs公式进行拟合,得到材料常数m=2.738,C=1.308×10-8,得到的Pairs公式为:
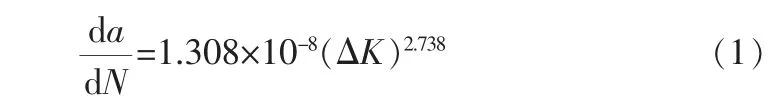
3 静力分析
3.1 几何和网格模型
压缩机气体入口管道中间有3个管卡来限制管子径向和周向的位移(图8)。管内介质为乙烯气体,根据管道参数建立管道有限元几何模型,并采用Solid185单元对管道进行网格划分。
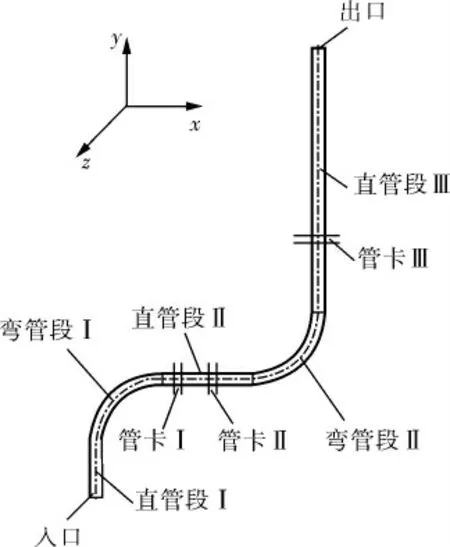
图8 管道结构示意图
管路设计基本参数如下:
操作压力 75 MPa
操作温度 40℃
管道内径 31.7 mm
管道外径 76.3 mm
管道材料 40CrNiMoA
40℃下管道材料部分性能如下:
许用应力Sm302 MPa
弹性模量Et201.615 GPa
泊松比μ 0.295
3.2 载荷和边界条件
静力分析所考虑的载荷包括管子自重和管子内部施加的75 MPa的压力载荷。载荷施加示意图如图9所示。管子两端添加固定约束,并约束图8中管卡Ⅰ、管卡Ⅱ和管卡Ⅲ位置管道的径向和环向位移,在模型中施加的约束如图10所示。
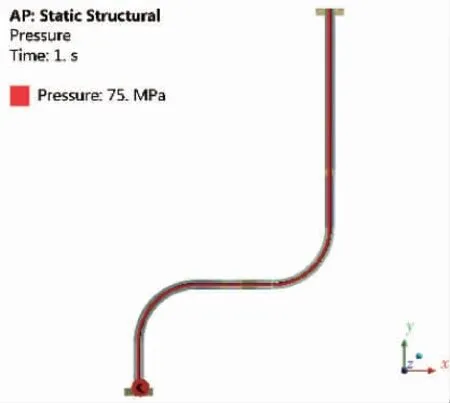
图9 载荷作用示意图

图10 约束示意图
3.3 静力强度计算结果及分析
笔者采用JB 4732—1995(2005年确认)《钢制压力容器——分析设计标准》对压缩机气体入口管道进行校核评定。设计强度校核许用值为Sm=302 MPa,1.5Sm=453 MPa,3.0Sm=906 MPa。
整体结构应力强度分布如图11所示。最大应力强度为168.37 MPa,远小于设计应力强度Sm,因此不需要进行应力线性化处理,静强度满足要求。
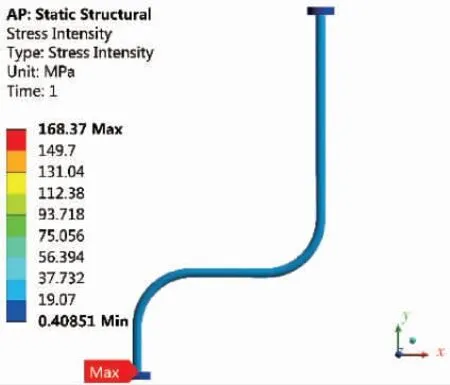
图11 管道应力强度分布
4 压缩机激发频率及管路气柱模态分析
4.1 管路气柱模态分析
在操作工况下,介质的物性参数为:声速1 146 m/s、密度490.7 kg/m3。管道与压缩机相连端视为声学闭端,与足够大容器相连端视为声学开端。笔者采用Fluid30声学单元对该模型进行网格划分。
计算得到管路前6阶气柱固有频率(表1)。

表1 气柱前6阶固有频率 Hz
4.2 压缩机激发频率
往复压缩机气体进口管道内压力脉动由气缸激发,激发频率f的计算公式为[8]:

式中 m′——压缩机气缸单或双作用方式,单作用时m′=1,双作用时m′=2;
n——压缩机曲轴转速,r/min。
该压缩机m′=1、n=200 r/min,计算得出的激发频率f=3.33 Hz。通常取0.8f~1.2f作为管道系统的共振区,即共振区为2.664~3.960 Hz。由表1可知,各阶气柱共振频率较高,没有落在共振区的气柱固有频率,故不发生气柱共振。
5 压力脉动分析
管内压力脉动分析采用计算流体动力学(CFD)方法对管内压力脉动进行计算。在操作压力介质比热容2.337 kJ/(kg·K),黏度83.6μPa·s。
5.1 进出口边界条件
管道与缓冲罐相连端为管道气体入口,设置为定常压力入口,压力为75 MPa。管道与压缩机相连端为管道气体出口,设置为质量流量出口。
由于气缸与管道之间设置了吸气阀。只有当气阀开启后,气缸中的气体与管道中的气流才建立一定的联系。为了简化求得与气缸相连的管道端点处的气流速度,做出如下假设:
a.忽略阀片运动对气流运动产生的影响,认为气阀的开启和关闭在瞬间完成。
b.气缸内气体的进、排气速度等于活塞的运动速度。因此,在气阀开启期间,气缸出口处气体速度正比于活塞速度,比例系数为气缸与管道的通流面积之比。
根据以上假设,对于单缸单作用的进气速度,在曲柄转动的一个周期内,气缸进口处即管道出口处的气流速度可以写成如下形式。
气缸吸气阀开启前:

气缸吸气阀开启期间:
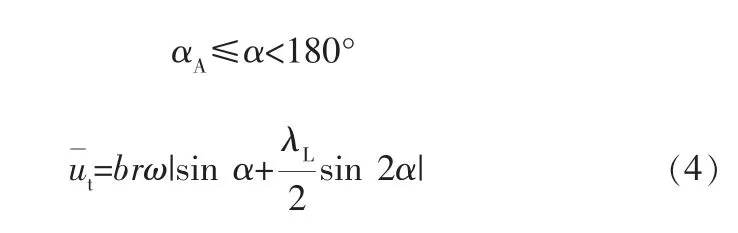
气缸吸气阀闭合后:

式中 b——气缸通流面积/管道通流面积;
r——曲柄长;
α——曲柄角;
αA——吸气阀开启角;
λL——曲柄长/连杆长;
ω——曲柄的角度。
根据压缩机参数可绘制管道出口速度曲线(图12)。
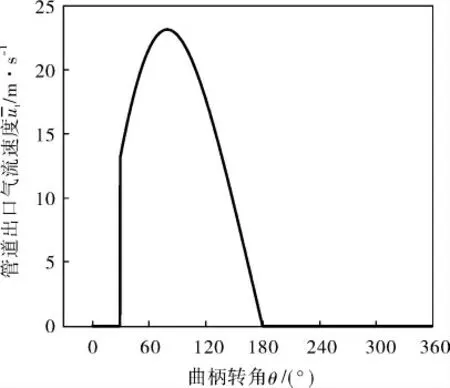
图12 管道出口速度曲线
压缩机参数如下:
转速 200 r/min
气缸内径 80 mm
吸气管内径 31.7 mm
曲柄长 170 mm
曲柄长/连杆长 0.2
吸气阀开启角 29.5°
管道出口气体最大流速为23.1 m/s,与声速1 146 m/s的比值为0.02,远小于0.3,所以可认为介质是不可压缩流体,密度可视为恒定。根据质量流量与流速的关系计算管道出口质量流量。管道出口的质量流量在曲柄旋转一个周期内的变化曲线如图13所示。
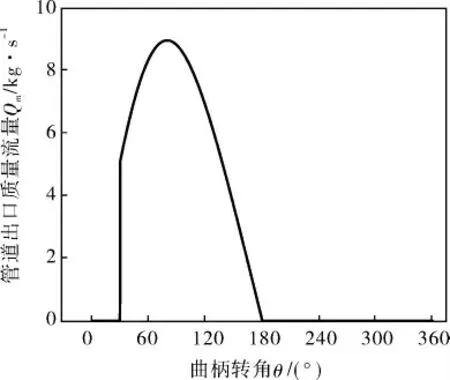
图13 管道出口质量流量曲线
5.2 计算结果及讨论
在管道上选取9个压力监测点(图14),监测点9静压力随时间变化曲线如图15所示。各监测点压力脉动峰峰值列于表2。

表2 各监测点压力脉动峰峰值
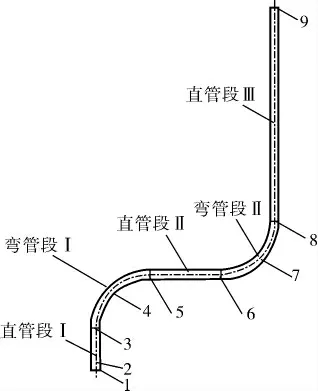
图14 压力监测点示意图
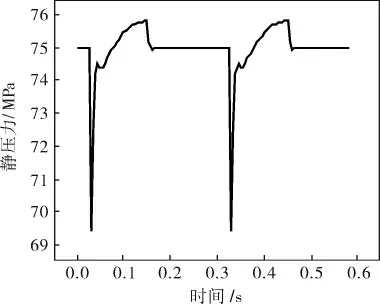
图15 监测点9静压力随时间变化曲线
压力脉动的程度可以用压力不均匀度δ来表征,其计算式为:
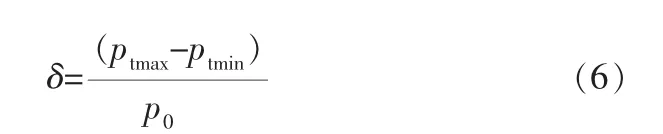
式中 ptmax——最大压力;
ptmin——最小压力;
p0——平均压力。
按式(6)计算出各监测点压力不均匀度(表3)。结合表2、3可以看出,压力脉动最大点在压缩机入口处的第9个监测点,其压力脉动峰峰值为6.414 2 MPa,压力不均匀度为8.55%。根据API 618标准中7.9.4.2.5.2.1规定,压缩机法兰处压力不均匀度应限制在7%内。脉动压力超标无疑影响管子疲劳寿命。
6 管路动力分析
6.1 管路模态分析
运用ANSYS模态分析模块对压缩机气体入口管道进行模态分析,选择Solid185实体单元对管道进行网格划分。管道入口端与出口端设为固定约束,管卡Ⅰ~Ⅲ的约束与3.2节中的相同。对管子采用有预应力的模态求解,求得的管道前6阶固有频率值见表4。由表4中数据可知,结构固有频率较高,没有落在共振区,所以结构不发生机械 共振。

表4 管道前6阶固有频率
6.2 管路谐响应分析
流体对管子的谐波力和相位为:

由表2测得的各点压力脉动峰峰值可以通过式(7)、(8)求得弯管处的激振力和相位。由于管道长度短,该工况下介质中的声速大,激振频率低,其相位差可以忽略。由监测点的压力脉动求得作用在弯管的激振力见表5。
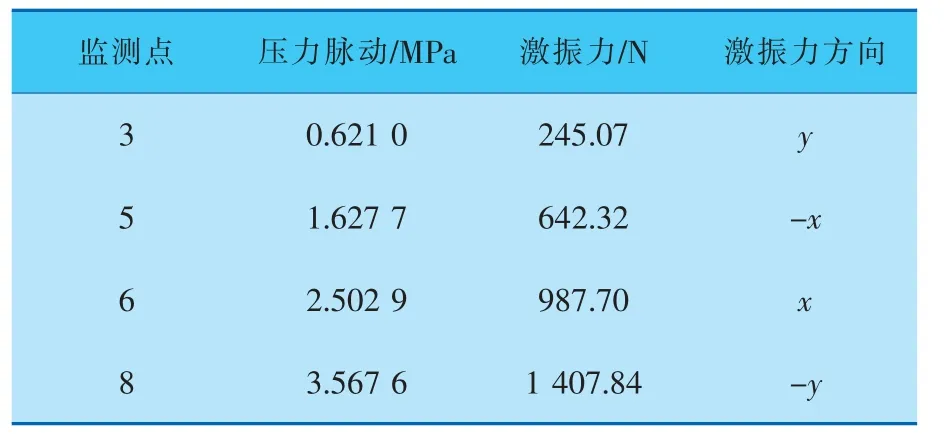
表5 作用在弯管的激振力
管道约束条件同6.1节。激振力载荷的施加如图16所示。
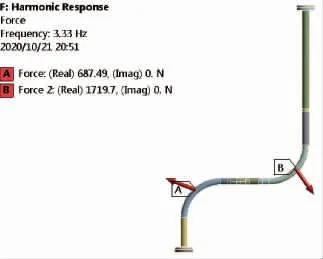
图16 激振力载荷的施加示意图
在3.33 Hz激振频率作用下管道x方向的振幅峰峰值为0.069 mm,y方向的振幅峰峰值为0.005 mm。根据API 618标准中7.9.4.2.5.2.4管路设计振动准则a,对于激振频率低于10 Hz的管路,规定的许用振幅峰值为0.5 mm。可见,管路振动符合API 618标准中7.9.4.2.5.2.4管路设计振动准则。
7 疲劳裂纹扩展及寿命计算
由表2可知,在与缓冲罐相连端,管道内压力脉动最大。在实际运行中,由于螺纹根部结构不连续,存在严重的应力集中,在疲劳载荷作用下,极易产生疲劳裂纹。另外,在螺纹加工过程中也可能产生微裂纹。因此,为估算管道疲劳寿命,这里假设在管道与缓冲罐相连的螺纹根部存在一深度为0.1 mm的微小表面裂纹。裂纹沿螺纹周向为半椭圆形,半椭圆长半轴c代表裂纹长度,短半轴a代表裂纹深度,c、a的不断变化会导致表面裂纹的形状发生变化。一般可用裂纹形状比a/c来反映其特征[9]。
7.1 三维含半椭圆型表面裂纹有限元模型
运用Ansys Workbench静力学分析模块中的Fracture在管道危险点插入椭圆裂纹,计算裂纹前沿各点的Ⅰ型应力强度因子。
根据管路谐响应分析可知,管路在简谐激振力作用下最大应力强度出现在管道与缓冲罐连接端管道外侧的螺纹上,如图17所示。文中假设裂纹在谐响应分析中应力强度最大位置处起裂。
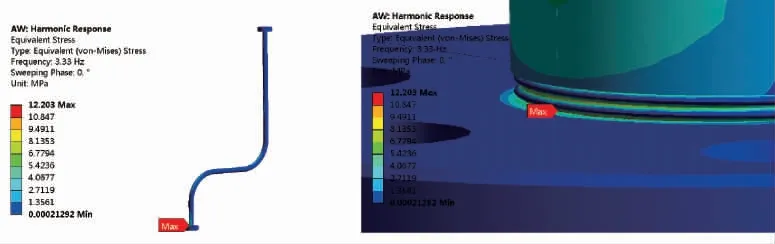
图17 谐响应分析应力强度
7.2 载荷和约束
管道约束条件与3.2节相同。根据压力脉动分析得到的各监测点的压力波动对管道内表面分段施加压力载荷。各段施加载荷见表6。
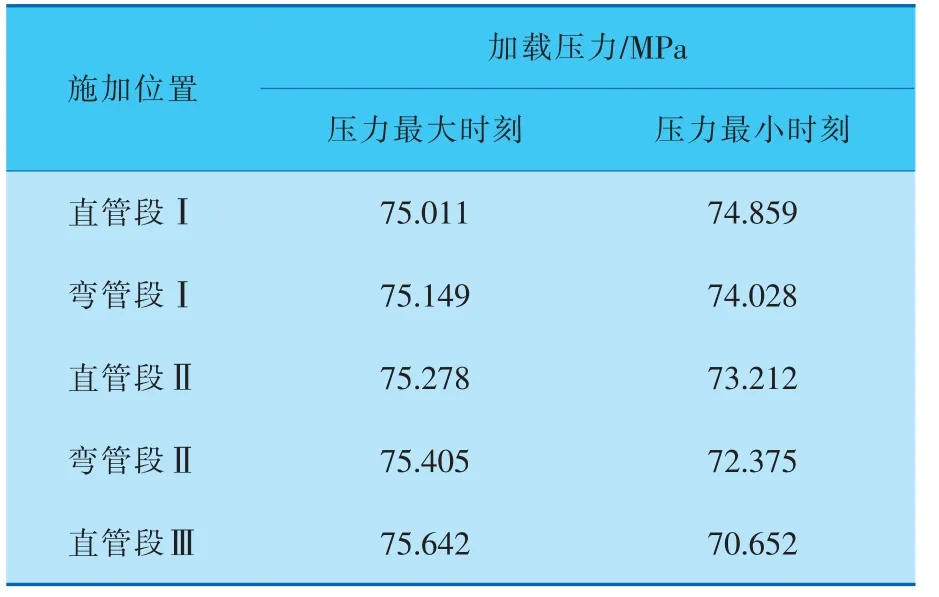
表6 各段施加载荷
7.3 裂纹扩展计算
应用式(1)计算裂纹的疲劳扩展,材料的Paris常数C和m已通过实验测定得到。只要知道扩展过程中某一时刻的短半轴a和长半轴c就可以确定半椭圆裂纹的形状。
首先设定有限元模型中初始裂纹的两个半轴长a0和c0,然后根据管道工作最大内压pmax和最小内压pmin,分别计算该裂纹最深点A和表面点B的应强度因子KAmax、KAmin、KBmax和KBmin,从而得到两点对应的应力强度因子变化范围ΔKA和ΔKB。经过ΔN个循环可由Paris公式分别计算出沿裂纹深度和表面两个方向上的扩展长度Δa和Δb。
由式(1)得:

对式(9)两边积分得:
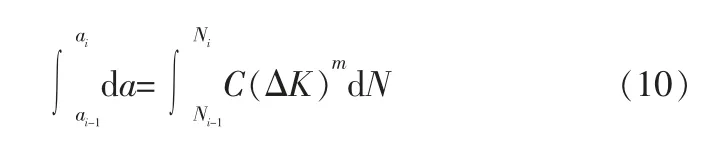
ΔN取值很小时,在ΔN个循环后裂纹扩展的深度很小,即ΔK变化很小,可认为是常量,积分结果为:

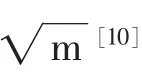
7.4 计算结果及讨论
设初始裂纹为a0=0.100 mm,c0=0.143 mm。裂纹扩展深度a与表面点B扩展弧长b的关系如图18所示。裂纹扩展深度a与应力强度因子范围ΔK的关系如图19所示。计算得裂纹扩展深度a与疲劳寿命的关系(图20)。
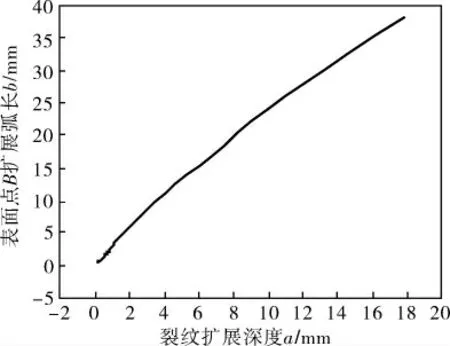
图18 裂纹扩展深度a与表面点B扩展弧长b的关系
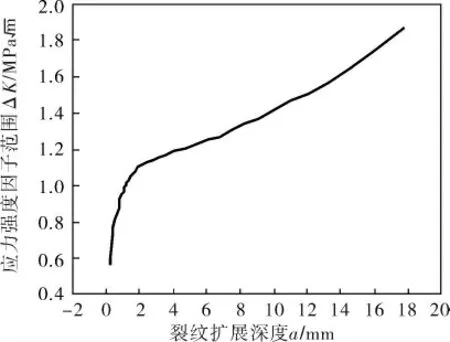
图19 裂纹扩展深度a与应力强度因子范围ΔK的关系
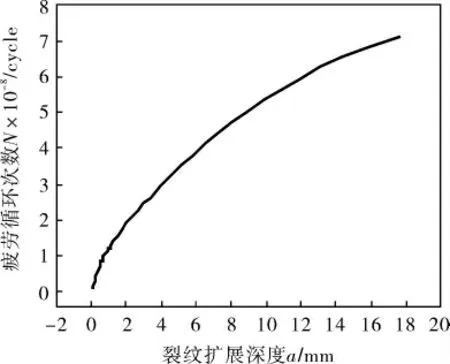
图20 裂纹扩展深度与疲劳寿命的关系
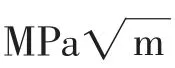
7.5 管卡刚度对疲劳寿命的影响
7.4节的计算结果是假设管卡Ⅰ~Ⅲ为刚性约束,即管卡对所约束管段的管子径向和环向有刚性约束,不允许出现任何位移。但实际管卡并非完全刚性,而是有一定弹性的,本节将分析管卡刚度的影响,即在保持加载不变的情况下,改变3个管卡的刚度,分别假设管卡刚度为20 000、15 000、10 000、7 500、5 000、0 N/mm情况下计算管道固有频率和疲劳寿命。不同管卡刚度下管道前6阶固有频率见表7。
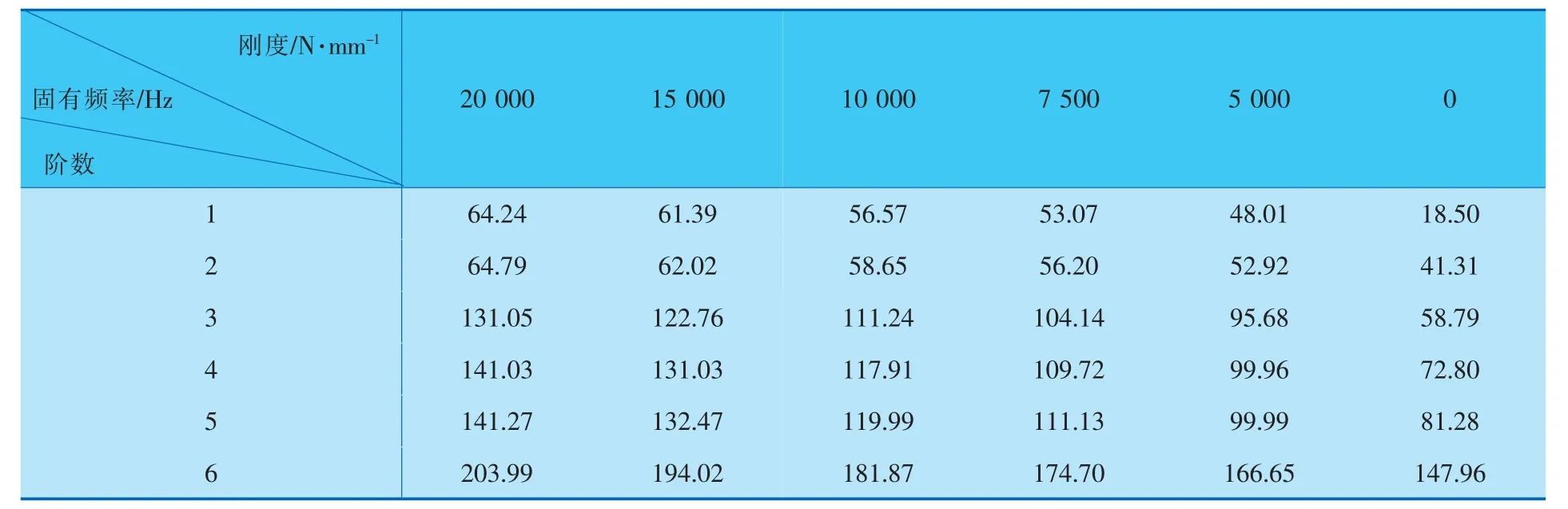
表7 不同管卡刚度下管道前6阶固有频率
不同刚度支撑下的裂纹扩展深度a与应力强度因子范围ΔK的关系如图21所示,不同刚度支撑下计算得到的疲劳寿命如图22所示。
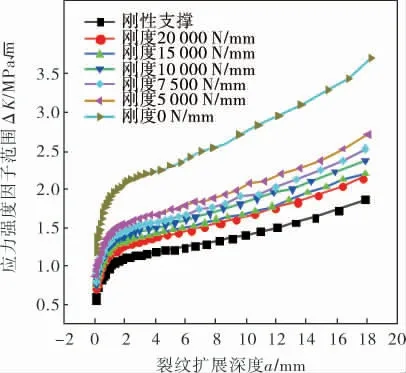
图21 不同刚度支撑下的裂纹扩展深度a与应力强度因子范围ΔK的关系
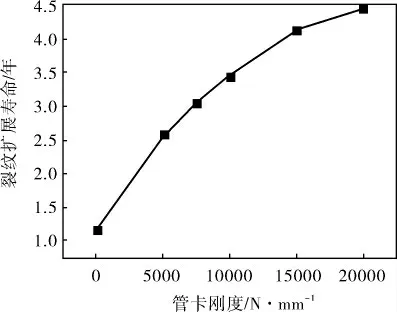
图22 不同刚度支撑下计算得到的疲劳寿命
由表7可知,不同管卡刚度下管道仍不会发生共振。而由图21、22可以看出,刚度越小,同样裂纹深度下应力强度因子越大,疲劳裂纹扩展寿命越短。所以,应对管道定期巡检,避免因振动导致管卡松动而减少管道使用寿命。
8 结论
8.1 经观察可见宏观断口上存在贝纹线,从贝纹凹凸方向可判断裂纹从外壁发生,向内壁扩展;微观断面上有疲劳辉纹,符合高周疲劳断裂特征。
8.2 对管道材料进行拉伸实验和疲劳裂纹扩展实验,测得了材料的弹性模量E和材料的Paris常数C和m值。
8.3 模态分析和谐响应分析表明,管路气柱与管路机械结构均不发生共振。而气体进口螺纹连接处压力不均匀度为8.55%,超过API 618限定值7%,压力不均匀度过大是导致断裂的主要原因。
8.4 在压力波动所引起的激振力作用下,管道上最大应力强度出现在气体进口螺纹根部,与管道实际的开裂位置一致。
8.5 若在管道螺纹根部出现微小裂纹,在管卡径向和周向刚性约束的条件下,由Paris公式计算出管道疲劳扩展寿命为6.8年。
8.6 若管卡为弹性管卡,刚度可以变化,则刚度越小,螺纹根部微小裂纹深度处的应力强度因子越大,疲劳裂纹扩展寿命越短。
