随机库水位作用下病险土石坝的失效概率研究

李 泽，彭 普，张小艳，谭志华

（1.昆明理工大学建筑工程学院，昆明 650500；2.昆明理工大学电力工程学院，昆明 650500；3.云南省水利水电勘测设计研究院，昆明 650021）

0 引 言

土石坝是指由当地土石料经过抛填、辗压等方法堆筑而成的挡水建筑物。目前我国在运行的8万多座土石坝水库中有接近3 万座为病险水库，这些病险土石坝大部分都是在20 世纪50-70年代修建的中、小型土石坝。由于受当时筑坝技术和资金投入等方面的限制，很多病险土石坝工程的建设标准偏低，在长期服役以后溃坝灾害时有发生，给人民财产安全造成重大损失［1］。病险土石坝的稳定安全问题是关乎国计民生的重大问题。国家相关部门已经开展了病险土石坝的全面调查和初步治理。

中小型病险土石坝具有以下特点：①由于特定的历史条件，坝体的填筑材料不良、抗渗性能不满足要求，长期服役以后坝体材料的物理力学性能严重衰减，与初始设计值相差较大；②长期服役后坝体材料的物理力学性能在时间、空间上都具有不确定性和随机性；③中小型土石坝水库的库容较小，一般为季调节水库，库水位受降雨和用水需求的影响在雨季和旱季呈现随机变化；④绝大部分中小型土石坝为均质坝体、无防渗墙，坝体的稳定性受库水位的影响较大。在当前关于土石坝稳定性的研究中还没有能够全面反映这些因素的研究成果［2］。

目前，在中国土石坝传统工程实践中普遍采用确定性分析方法进行土石坝的稳定性计算。我国土石坝规范推荐使用极限平衡分析法（LEM）对土石坝进行稳定性分析［3］，其通过事先假定滑裂面并对滑裂面上的土体进行条分，并对条间力的方向进行假定将超静定问题转化为静定问题，LEM 法概念清晰、计算简便且工程应用非常广泛；但该方法未能考虑土石坝的应力-应变关系，因此不能给出坝体的应力场、位移场［4，5］。同时，以有限单元法（FEM）和有限差分法（FDM）为代表的数值分析方法在土石坝稳定性分析方面得到广泛应用，其能使土体同时满足静力平衡条件、应变相容条件和本构关系，可以处理任意的土层、几何形状、荷载和边界，不仅可获得坝体详细的应力-应变分布而且可以获得比LEM 方法更合理的稳定性分析结果［6～9］；但其存在初始应力难以确定、岩土本构关系复杂等困难。

病险土石坝的稳定性与坝体材料的物理力学参数、库水位随机变化等因素密切相关。因此，土石坝的稳定性问题是一个与材料抗剪强度参数和库水位的随机性相关的不确定性问题，对于不确定性问题需采用可靠度分析方法进行研究。我国水利水电行业规范规定土石坝的设计在单一安全系数法的基础上需采用以概率理论为基础、以分项系数表达的极限状态设计方法进行稳定性验算［10］。同时，众多学者基于概率理论开展了土石坝的可靠度研究，可靠度方法在土石坝工程中得到充分重视和应用［11-17］。

在现有的土石坝可靠度分析中使用的稳定性计算方法主要以刚体极限平衡法（LEM）、有限单元法（FEM）为主［18-21］，同时塑性极限分析方法（UBM）在土石坝的可靠度分析方面得到深入研究［22-24］。相对于LEM 和FEM，塑性极限分析方法在寻求土石坝的极限状态方面存在理论上的优势，根据极值定理其可以高效、准确地获取土石坝破坏时的极限状态（应力场和速度场）。鉴于此，本文同时考虑土石坝土体的抗剪强度参数的变异性以及库水位的随机性，将塑性极限分析上限法理论、有限元离散思想、数学规划理论、蒙特卡洛方法结合起来对病险土石坝的可靠度进行研究。

1 土石坝的极限状态功能函数

本文同时考虑土体抗剪强度参数和上游库水位的随机性，则土石坝的稳定性与凝聚力、摩擦角以及上游库水位相关；使用文献［25］的方法，本文采用容重超载法使土石坝达到破坏的极限状态。在进行可靠度分析时，病险土石坝的极限状态功能函数可表示为：

式中：cr和φr分布是土石坝土体的凝聚力随机量和摩擦角随机量；Hrw是上游库水位随机量；km(cr，φr，Hrw)是与cr、φr和Hrw相关的安全系数随机量；当Z＞0时表示土石坝整体稳定，当Z=0时表示土石坝处于临界状态，当Z＜0 时表示土石坝发生失稳（失效）。

土石坝的上游库水位在最低水位与最高水位之间随机变化，库水位一般在死水位至校核洪水位范围内随机变化，并近似服从正态分布，本文采用截尾正态分布模拟库水位的变化。库水位随机数按下式进行生成：

式中：tw=(1，…，nw)，nw是土石坝上游库水位蒙特卡洛随机数的数量；Hrw(tw)是库水位的第tw个随机数；μw是库水位的均值；σw是库水位的标准差；Random是正态分布随机数生成函数；Normal表示库水位随机数符合正态分布；Hlb是库水位的下界，取最低水位；Hub是库水位的上界，取最高水位。

假设土石坝土体材料的凝聚力和摩擦角均符合对数正态分布，其随机数按下式生成：

式中：tm=(1，…，nm)，nm是土体材料凝聚力和摩擦角蒙特卡洛随机数的数量；cr(tm)是土体材料凝聚力的第tm个随机数；φr(tm)是土体材料摩擦角的第tm个随机数；μc是土体材料凝聚力的均值；μφ是土体材料摩擦角的均值；σc是土体材料凝聚力的标准差；σφ是土体材料摩擦角的标准差；Random是正态分布随机数生成函数；lognormal表示随机数符合对数正态分布。

在同时考虑库水位、抗剪强度参数的随机性时，定义土石坝的安全系数如下：

式中：tw=(1，…，nw)，tm=(1，…，nm)，c′r(tm)是强度折减以后土体材料凝聚力的第tm个随机数；φ′r(tm)是强度折减以后土体材料摩擦角的第tm个随机数。

2 土石坝上限法数学规划模型

塑性极限分析的上限定理是求解岩土体承载力的高效工具，上限法的原理是：通过构建土石坝的机动许可速度场，机动许可速度场需同时满足：三角形单元塑性流动约束条件、公共边速度不连续约束条件、三角形单元速度边界约束条件；每个机动许可速度场对应有唯一的外荷载，根据上限定理可知最小外荷载必然最接近其真实的极限荷载。所以，上限法本质上可归结为一个求极小化的数学规划问题。本文在前人的研究基础上［26，27］，基于上限定理建立土石坝可靠度分析的上限法数学模型。

2.1 数值离散

本文使用非共结点的三角形单元离散土石坝［如图1（a）所示］［23，26］，三角形单元的每个结点具有沿x方向的速度uexi、y方向的速度ueyi，其中i=(1，2，3)；同时，受随机库水位作用单元的每个结点具有孔隙水压力随机量prei，其中i=(1，2，3)。为了构建土石坝的机动许可速度场，相邻有限单元之间公共边需存在速度间断，相邻有限单元之间公共边的速度间断如图1（b）所示，一条公共边共有标号①②③④的4 个结点，其中结点①③属于单元a、②④属于单元b，公共边的每个结点具有沿x方向的速度udxi和y方向的速度udyi，i=(1，2，3，4)。

2.2 土石坝的稳定渗流计算

为了获得土石坝中每一点的孔隙水压力，本文采用稳定渗流理论对随机库水位作用下的土石坝进行渗流场分析［28］。二维稳定渗流公式如下：

式中：kx是土体材料x方向的渗透系数，ky是土体材料y方向的渗透系数，Hr是土石坝内各点的随机水头函数。

2.3 上限法数学模型的约束条件

（1）三角形单元塑性流动约束条件。假设土石坝土体为理想刚塑性体且符合相关联流动性法则，则土体由变形协调条件得到的塑性应变分量等于由关联流动法则和屈服条件所得塑性应变率分量。土石坝三角形单元塑性流动约束条件可表示为：

式中：e=(1，…，Ne)，Ne是土石坝中所有有限单元的数量；Ae是有限单元e的面积。

由于篇幅有限，系数be1，be2，be3，ce1，ce2，ce3和Ak，Bk，Ck，k=(1，…，m)等的涵义详见文献［26］。

（2）公共边速度不连续约束条件。塑性极限分析上限法规定在土体相连单元公共边上速度可间断但必须符合相关联流动法则，则相连有限单元公共边速度不连续约束条件：

式中：d=(1，…，Nd)，Nd是土石坝中所有有限单元公共边的数量；分别是单元公共边d的4 个非负塑性乘子；θd是公共边的倾角，逆时针为正；φr(tm)是土石坝土体材料摩擦角的第tm个随机数。

（3）三角形单元速度边界约束条件。土石坝边界上的三角形单元速度场必须满足已知的边界条件。在速度为0的边界上土石坝坝体三角形单元速度边界条件为：

式中：Ab是边界上的有限单元b的坐标转换矩阵；ub是边界b的速度向量；b=(1，…，Nb)，Nb是土石坝中边界上速度等于0 的有限单元的数量。

2.4 上限法数学模型的目标函数

根据功能原理，在整个土石坝中内力做的内功功率应该等于外力做的外功功率。当土石坝内有孔隙水压力作用，并考虑容重超载时，土石坝的内功功率与外功功率相等条件为：

式中：We是有限单元的内功功率；Wd是有限单元公共边的内功功率；WG是自重在有限单元结点速度上所做的外功功率；W pe是孔隙水压力在有限单元连续体内所作的外功功率；W pd是孔隙水压力在有限单元公共边上所作的外功功率；kγ(tw，tm)是与第tw个随机库水位和第tm个抗剪强度参数对应的容重超载系数。

土石坝内有限单元的内功功率为：

土石坝内有限单元公共边的内功功率为：

式中：ld是公共边的长度。

土石坝中土体的自重在有限单元结点速度上所做的外功功率为：

式中：γe是单元的土体容重。

土石坝内部的孔隙水压力在有限单元连续体内所作的外功功率：

土石坝内部的孔隙水压力在有限单元公共边上所作的外功功率为：

式（9）是一个非线性表达式，为了避免求解非线性规划问题，本文将其进行线性化处理。根据上限定理可知，机动许可速度场中结点的速度表示单元相对于固定边界发生塑性流动的相对大小，其与物理学上的速度的概念不同，其仅仅表示单元发生塑性流动的趋势；因此，本文增加一个附加约束，设WG=1.0，将式（9）等效变换为两个数学线性式：

根据上限定理：与机动许可速度场对应的所有外荷载中，最小的外荷载与真实荷载最接近，即：上限法是求一个外荷载的极小值的数学规划问题。因此，考虑土石坝土体容重超载时，可设容重超载系数为目标函数，求解土石坝稳定性的上限法目标函数为：

式中：Minimize表示求“最小”。

2.5 土石坝可靠度分析上限法数学规划模型

根据土石坝坝坡极限状态函数式（1），目标函数式（17），约束条件式（6）、（7）、（8）、（16），可以得到随机库水位作用下的土石坝可靠度分析上限法数学规划模型：

式（18）是一个大型的线性规划数学模型，其中的A2e、A2d、We、Wd、W pe、W pd都与土体的抗剪强度参数、库水位随机变量相关。当使用式（2）、式（3）分别将抗剪强度参数随机变量（cr，φr）、孔隙水压力随机变量（Hrw）离散成若干个随机数［cr(tm)，φr(tm)，Hrw(tw)，其中tw=(1，…，nw)，tm=(1，…，nm)］以后，式（18）相应地变成nw×nm个线性数学规划模型，通过数学规划算法求解可以获得nw×nm个安全系数以及对应的速度场。

3 土石坝的失效概率和可靠度指标

在当前，土石坝失效分析主要使用整体失效概率法，即根据土石坝的安全系数来求解土石坝的整体失效概率，其原理是：当土石坝的安全系数≥1 时土石坝是稳定的（整体安全）、当土石坝的安全系数＜1 时土石坝发生失稳（整体失效）。土石坝的失效功能函数如下：

式中：tw=(1，…，nw)，tm=(1，…，nm)，I(tw，tm)是第tw个库水位作用下对应着第tm个抗剪强度参数随机数的土石坝失效功能函数。

土石坝在第tw个库水位作用下的整体失效概率按下式计算：

式中：tw=(1，…，nw)，Pzf(tw)是土石坝在第tw个库水位作用下的整体失效概率。

在所有的nw个库水位作用下土石坝的失效概率按下式计算：

式中：PzF是土石坝在所有可能发生的地下水位作用下的整体失效概率。

土石坝第tw个库水位作用下安全系数的均值：

式中：tw=(1，…，nw)，μk(tw)是第tw个库水位作用下土石坝nm个安全系数的平均值。

土石坝第tw个库水位作用下安全系数的标准差：

式中：tw=(1，…，nw)，σk(tw)是第tw个库水位作用下土石坝nm个安全系数的标准差。

在所有的nw个库水位作用下土石坝安全系数的均值：

式中：μk是nw×nm个安全系数的平均值。

在所有的nw个库水位作用下土石坝安全系数的标准差：

式中：σk是nw×nm个土石坝安全系数的标准差。

4 土石坝可靠度分析上限法数学规划模型的数值求解策略

图2是随机库水位作用下病险土石坝可靠度分析上限法数学规划模型的数值求解流程，计算主要包括3个部分：前处理模块、计算模块和后处理模块，具体步骤如下：

（1）确定土石坝坝体几何参数、土石坝材料的物理力学参数、材料的抗渗参数和库水位信息；

（2）建立土石坝可靠度计算的极限状态函数；

（3）生成水库上游库水位水头的随机数；

（4）生成土石坝坝体材料的抗剪强度参数的随机数；

（5）使用三角形有限单元离散土石坝，根据步骤（3）生成的库水位水头信息，进行土石坝的稳定渗流计算，获得有限单元节点的孔隙水压力；

（6）根据式（18）构建满足目标函数、约束条件的病险土石坝稳定性分析上限法线性规划模型；

（7）使用“对偶单纯形法”求解病险土石坝稳定性分析上限法线性规划模型得到对应的安全系数；

（8）计算土石坝安全系数的均值、标准差以及土石坝的失效概率。

5 工程实例分析

根据本文提出的方法，编制了相应的上限法程序，并对云南省某病险土石坝进行了计算分析，将计算结果与LEM 法的计算结果进行比较，验证了本文计算方法的正确性。

5.1 云南省某病险土石坝概况

某病险土石坝位于云南省中部，大坝为均质坝（如图3所示），坝顶高程为1 873.00 m，最大坝高为22.5 m，坝顶长度为110 m、宽度为3.5 m，上游坝坡坡比为1∶2.75、下游坝坡坡比为1∶2.60。该坝在初期建造时采用当地材料进行筑坝，受历史原因、投入资金的限制，该土石坝设计水平和施工质量偏低；经过54年的长期服役，坝体材料的物理力学性质已经严重劣化，坝体的稳定性已不满足现行规范要求；经过鉴定，该土石坝属于B类病险土石坝，需要进行综合治理。为详细了解该病险土石坝的实际情况，勘察单位在大坝坝体区域布置了4 个地质钻孔（ZK1～ZK4）对土石坝进行了地质勘察，勘察结果显示：土石坝坝体黏土的力学性质较差；坝基地层分为两层，表层为砾石土，下层为石英质粉砂岩，力学性质相对较好；库区水文工程地质条件好，库水不存在向库外邻谷渗漏问题。表1为土石坝在设计初期和长期服役以后的材料物理力学参数统计表。

表1 土石坝材料物理力学参数的设计值及当前值Tab.1 Design values and current values of material parameters of earth-rock dam

本文采用三角形单元对土石坝进行离散，得到1 235 个三角形有限单元，3 705 个不共节点单元，1 788 条公共边，坝体网格划分如图4所示；建立xoy坐标系如图所示，水平向右为x轴正向，竖直向上为y轴正向，坐标原点O的高程为1 834.59 m；图中P1、P2、P3、P4为孔隙水压监测关键点。

5.2 随机库水位和稳定渗流场

该水库为小（二）型水库，校核洪水位1 871.39 m，正常蓄水位1 871.10 m，死水位1 857.85 m，水库总库容57.2 万m³。该水库为季调节水库，库水位受降雨和用水需求的影响在雨季和旱季呈现随机变化；根据该水库历年的水文资料统计分析，上游库水位Hw在死水位到校核洪水位范围内随机变化，近似服从正态分布，本文假设Hw服从截尾正态分布规律。根据式（2）离散获得Hw的随机数，取水库上游死水位为水位下界，即Hlb=27.56 m（绝对高程1 862.15 m），取水库校核洪水位为水位上界，即Hub= 40.43 m（绝对高程1 871.39 m），库水位均值Huw=37.00 m，变异系数为0.3，取随机数量nw= 50，上游库水位随机数分布情况如图5所示。

根据生成的库水位随机数，计算得到该病险土石坝的50个稳定渗流场。图6为在低水位、中水位、高水位作用下土石坝的孔隙水压力等值线分布图。随着水位的升高，土石坝的浸润线随之升高，坝体内的孔隙水压力值也随之增大。由于该土石坝的坝体未设置防渗体，浸润线变化平缓，在高水位作用时，大部分坝体处于饱和状态，孔隙水压力对坝体的稳定性有较大的不利影响。

图7为土石坝中4 个关键点的孔隙水压力随水位变化关系图。随着水位的增加，关键点的孔隙水压力值随之增加。关键点的孔隙水压力表现出如下规律：①在相同水位作用下，随着关键点向下游移动，孔隙水压力值不断减小；②越靠近上游面的关键点，其孔隙水压力值变化越激烈，如：最靠近上游的P1关键点的孔隙水压力值从-0.14 kPa升高至-114.07 kPa，而靠近下游面的P4 关键点的孔隙水压力值从-0.02 kPa 升高至-30.54 kPa。

5.3 上限法与LEM法的对比分析

根据表1可知，该土石坝经过50年的服役，坝体材料的抗剪强度参数已大幅降低（降幅在22%～25%之间），本文选用上游库水位随机数的部分样本，采用本文上限法和LEM 法对土石坝在设计初期和长期服役后的可靠度进行对比分析计算。计算结果如表2和图8、9所示。

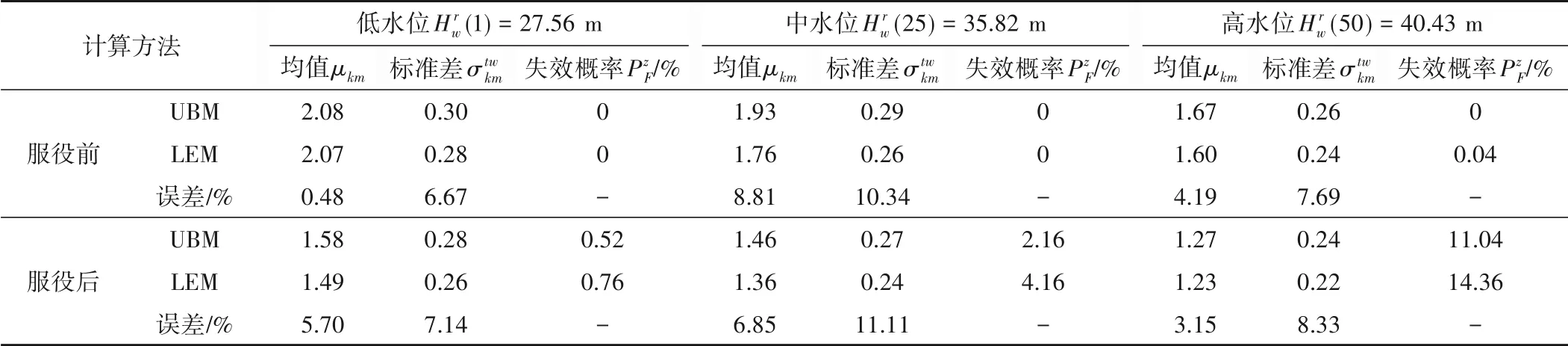
表2 可靠度指标的计算结果Tab.2 Calculation results of reliability index

图8为Hrw(1) = 27.56 m的低水位作用下土石坝安全系数累积概率密度曲线，由图8可知本文上限法与LEM 法在两种工况下的曲线都比较接近，误差较小，上限法曲线位于LEM 法曲线的上方，表2为土石坝在Hrw(1)、Hrw(25)、Hrw(50)时上限法和刚体极限平衡法计算所得可靠度指标。

从图8可以直观地看出，不管是设计值曲线还是服役后的曲线，UBM 和LEM 法的计算结果都非常接近。服役前的均值误差为0.48%，服役后的均值误差为5.70%，验证了本文计算方法的正确性。采用两种计算方法所得设计值累积概率密度曲线均位于服役后的曲线左侧，即经过长期的服役后土石坝安全系数大幅降低，与土石坝的实际情况相符。

从计算的结果可以得出：在服役前后土石坝安全系数的均值、标准差的上限解均小于LEM 法的计算结果，但误差较小，服役前后采用两种计算方法均值的最大误差为8.81%，标准差的最大误差为11.11%；此外，服役前后采用本文计算方法所得安全系数的均值在低水位时降低24.04%、中水位时降低24.35%、高水位时降低23.95%，服役前后采用LEM 法所得安全系数的均值在低水位时降低28.02%、中水位时降低22.73%、高水位时降低23.13%。服役前后采用本文计算方法所得失效概率在低水位时增加了0.52%、中水位时增加了2.16%、高水位时增加了11.04%，服役前后采用LEM 法所得失效概率在低水位时增加了0.76%、中水位时增加了4.16%、高水位时增加了14.32%。服役前，土石坝在低、中、高水位时失效概率均较低，安全性较高；服役后，土石坝在高水位时失效概率较高，安全性较低。

图9为土石坝失稳时上限法速度场，可以看出，采用上限法所得速度矢量围成的区域和LEM 法所得临界滑裂面基本一致，但部分区域存在差距。这是因为采用LEM 法进行土石坝稳定性计算时，需要事先假定滑裂面的位置，然后对假定滑裂面上土体进行条分，通过对各条块受力特征进行分析，从而得到临界滑裂面位置，从理论上讲，LEM 法所得滑裂面是假定滑裂面，与真实滑裂面存在差距；上限法通过有限单元构建土石坝可靠度上限法数学规划模型，采用数学规划的方法搜索得到坝体的失稳区域，其结果更加接近于真实情况。

5.4 长期服役时的坝体可靠度分析

该土石坝经过长期的服役，土石坝材料抗剪强度参数下降，勘察单位对该土石坝材料的抗剪强度参数进行试验测定，根据勘察发现坝体土和排水棱体的黏聚力和内摩擦角相较于设计值均有所降低，其中坝体土和排水棱体的黏聚力降低了22.86%，内摩擦角降低了25%。本文假设黏聚力和摩擦角均服从对数正态分布，样本数量取为nm=5 000，根据以上信息，生成坝体材料抗剪强度参数随机数如图10所示。

图11、12分别土石坝安全系数概率密度曲线和累积概率密度曲线，图13、14 为计算所得土石坝安全系数的均值和标准差随水位的变化关系。根据计算结果可知，安全系数概率密度曲线基本服从正态分布，且随着库水位的升高，概率密度曲线和累积概率密度曲线均逐渐左移，土石坝的安全性降低，失效概率逐渐增大，可靠度指标逐渐降低。此外，随着库水位的升高，安全系数的标准差也在逐步减小，概率密度曲线的分布范围逐步变窄，累积概率密度曲线逐步变陡。

图15、16为计算得到的安全系数均值和标准差直方图。安全系数均值在1.55～1.57 区间内出现的频数最多，最高频次为8次；安全系数标准差在0.267～0.270 和0.283～0.286 区间内出现的频数最多，最高频次为7次。

本文统计了50个随机库水位作用下土石坝的失效概率（如图17 所示）。从图中可以看出随着库水位的升高，失效概率从0.52%增加到11.04%，安全性逐步降低。库水位在27.56～34.00 m 范围内，失效概率随水位变化较小；库水位在34～38 m 范围内，失效概率随水位变化开始增大；库水位在38.00～40.43 m 范围内，失效概率随水位变化急剧增大。土石坝的失效概率随库水位的升高整体上呈现先平稳后上升、再急剧上升的特征。库水位主要通过影响土石坝内部稳定渗流场从而影响坝体稳定性，在水位较低时，只有坝基和少部分坝体处于饱和状态，随着水位的升高，坝基和坝体处于饱和状态的面积增大明显，这就使得土石坝在水位较高时，安全性面临一定的挑战。对此，在土石坝实际运行过程中，应该采取以下措施，从而保证土石坝的安全：

（1）在土石坝运行过程中应该避免高水位的出现，在洪水期，当水位超出38.00 m 时，应该及时采取相应措施，如开闸泄水的方式来降低库水位，从而保证土石坝的正常运行。此外，由于土石坝在多年的运行过程中，材料的抗剪强度参数会降低，土石坝安全性能降低，通过固结灌浆的方式可提高材料的强度，提高土石坝安全性能。

（2）由于土石坝在长期的浸泡和冲刷过程中，渗透系数会显著增大，坝体内部孔隙水压力值也会明显增加，对病险土石坝做防渗处理极为必要，如：通过建立防渗墙的方式，降低坝体内部的孔隙水压力，从而增加坝体稳定性；将贴坡排水体改为褥垫排水从而降低坝体浸润线，减少坝体内部处于饱和状态的面积，从而增加坝体稳定性。

7 结 论

（1）本文将上限定理、有限元离散技术、数学规划理论和蒙特卡洛方法结合起来，同时将病险土石坝坝体材料的抗剪强度参数和上游库水位作为随机变量，建立了病险土石坝可靠度分析的上限法随机规划模型，并编制了相应的计算程序，获得了同时考虑土石坝坝体材料的抗剪强度参数和上游库水位随机性的土石坝安全系数、失效概率分布规律，为病险土石坝可靠度分析提供了一种新方法。

（2）本文获得了病险水库的库水位对土石坝的安全系数分布的影响规律，在相同土体的抗剪强度参数样本下，随着库水位的不断升高，安全系数的均值、标准差均呈现下降趋势。同时，库水位对土石坝的整体失效概率有较大影响，失效概率随着库水位的升高不断增大，且呈现先平稳后上升再急剧上升的特征，对此，在实际工程中，针对病险水库，库水位过高应该及时通过开闸泄水的方式使库水位降低，也可以通过对病险土石坝做防渗处理的方式，提高大坝安全性。

（3）本文是将塑性极限分析引入病险土石坝可靠度分析的有益探索。在实际工程中，地震和库水位是影响土石坝稳定性的两个重要因素，由于计算工作复杂，难度较大，本文研究内容仅考虑了库水位对病险土石坝的影响，未考虑地震的作用。在今后的研究工作中，应着重对地震作用下病险土石坝可靠度研究工作。□