数形可视化的认识与应用

“数”与“形”是数学两大基本概念，数形结合的本质是一种模式转换为另一种模式^[1]，教师开展数形结合教学有助于学生利用已知探索未知。数形可视化不限于数学学科，也适用于多学科整合。教师引导学生掌握“数”“形”概念，有利于培养他们的创新思维能力。笔者结合数学和音乐教学实践介绍数形可视化的应用。

一、认识数形可视化

（一）数形可视化的定义和演化过程

数形可视化是利用信息技术将抽象概念转换成数形图像，帮助学习者直观感知，使抽象问题具体化、繁杂文字数据条理化，进而解决问题的过程^[2]。具体来讲，它是运用软件和技术，以学习者为中心，按照认知规律，将对数字的感知、认知、想象、推理及其发展变化过程，转换为可视化资源，帮助学习者有效学习的方式。

笔者从数形分化、数形结合、数形可视化三个阶段阐述数形可视化的演化过程。其一，从数形分化来看，教师基于现象进行数与形的抽象，用数和形解释当前所看到的现象或者问题，用数来表征概念，用形来重组概念，分别发挥其不同作用，帮助学生认知现实世界。其二，从数形结合来看，将数与形的特点进行结合，用原有的数、形的抽象概念解释现象，通过数形结合来将抽象概念具体化、简单化，发挥数之“以数助形”和形之“以形解数”的作用，并且数与形是双向可逆的。其三，从数形可视化来看，充分利用信息技术支撑，以学生为中心，根据认知规律，用数字化图像可视化表征数形结合，让转化者和使用者更加直观地理解数与形表达的抽象概念，有效学习、深入理解。

（二）数形可视化的特点

数形结合，力求“以形助数”与“以数解形”，坚持“利、逆、高”的发展理念，以适应智能化教与学的变革。利，就是有利转换，通过信息技术、智能化、软件呈现等，降低学习者认知成本。逆，就是可逆转换，通过交互与可逆转换，呈现认知最佳点，帮助学习者有效学习、有效归纳。高，就是高度可视化和高度提炼，不论是理论到实践的化归，还是实践到理论的提炼，高度转换就能降低学习成本、认知成本和制作成本。

（三）数形可视化的类型

目前，软件工具趋于模板化、智能化、操作简单化，有利于使用者掌握，实现数形可视化。数形可视化分为两类：一类为抽象到具体的正向转化;另一类为具体到抽象的逆向化归。正向转化包括“文字和数据可视化”“思维与推理过程可视化”“抽象问题具体化”等。在开展文字意境理解、定理推论证明、技能实操演示等教学时，教师可通过可视化（呈现），帮助学生更好地理解知识，解决问题。逆向化归包括“思想统筹”“数据整理”“结论化归”等。在开展数据统计分析、观点宏观提炼等教学时，教师通过合理的分析与提炼，帮助学生更好归纳内化。正向转化与逆向化归并不孤立，二者相辅相成，紧密围绕有利转换和最佳呈现，为“减负”与“提效”服务。

二、设计准则与教学策略

（一）数形可视化的设计准则

数形可视化的设计应当遵循表达准确、转换精确、重点清晰、体贴和谐四项原则。所谓表达准确，就是数形可视化的设计应当为学生提供理解每阶段内容学习所需的前后联系元素，将文字、数据进行准确的可视化，确保知识表达的准确性。为何强调转换精确，因为双向转换存在误差，转换准确率的高低决定了“减负率”，也决定了“学与教”效率的高低。数形可视化的设计应当做到有利转换与精确转换。双向转换表达要清晰，特别是重点或要点，言简意赅、清晰表达，能快速引导学生的注意力集中到最重要的知识点上，减轻认知负担，数形可视化的设计与选材应当小而精，尽量以单一重点或要点为背景，这就是重点清晰准则。数形可视化的设计以学生为中心，以学习认知为出发点，设计并不针对个体，而是充分考虑学生的学习诉求，进行引导，使交互更友好、更普适，这就是体贴和谐准则。

（二）数形可视化的教学策略

数形可视化的应用必定基于库的建设。库，需要学习者与教学者或研究者（以下合称教研者）共同建构，需要集体的同化与顺应，需要互联网、软件和技术智能化的支持。教研者创建数形可视化云端，学习者在纸上（或设备上）完成作品后，可通过设备扫描，上传至云端。教研者下载作品至PC端，借助软件与技术，作可视化或抽象化处理，反馈到学习者，并积累入库。库与库之间，共创、共生、共享、共赢，服务于教学。入库后，任何时段，学习者或教研者都可链接库，检索（如“凸多边形外角和”“正三角形内任意点到三边的距离和等于正三角形的高的证明”“检验”“演唱技巧”等），即可调用资源，进行教研或学习。

当库满足学习者需求，学习者只需通过设备与网络，访问库，检索关键词，选择适当资源，即可个性化学习;如库暂时无法满足需求，可通过寻求教研者帮助，共建库，以满足学习者需求，共享共赢。通过库与库的链接，构建更大库，扩大资源数量与覆盖面。学习者可为教研者，教研者可为学习者，相辅相成，共建共生。

三、数形可视化典型案例与效果分析

（一）凸多边形外角和360°的证明

笔者通过实验，实现数形可视化，利用Geogebra软件，呈现三角形、四边形、五边形、六边形等凸多边形的外角（可随意改变多边形的边长与形状），利用函数，显示多边形每个外角的度数以及求和结果。笔者设置可控制条，拉动多边形外角的边（可逆，往外或往内），逐步将多边形拉紧，直到多边形变为一个点，多边形外角和形成一个周角360°（如图1）。笔者借助软件进行直观演示，引发学生思考：“凸多边形外角和是否都是360°？”

学生这是通过实验、观察，猜想：多边形的外角和等于360°。笔者接下来给出它的数学证明，让学生明白“凸多边形外角和360°”本质上是三角形的内角和等于180°，多边形与圆有着密切的联系。

凸边形的内角和等于（-2）×180°。凸边形每一条边都存在1个内角和1个外角，且该内角和外角组成平角（180°）。

1.在三角形中：3个内角+3个外角=3个平角[三角形内角和（3-2）×180°=180°]。

180°+外角和=3×180°=540°，故外角和为360°。

2.在四边形中：4个内角+4个外角=4个平角[四边形内角和（4-2）×180°=360°]。

360°+外角和=4×180°=720°，故外角和为360°。

3.在五边形中：5个内角+5个外角=5个平角[五边形内角和（5-2）×180°=540°]。

540°+外角和=5×180°=900°，故外角和为360°。

……

证明是基于凸多边形内角和进行的。笔者在证明过程中引导学生从三角形开始，逐渐推广到四边形、五边形……随着凸多边形边数增加，图形和证明都趋于复杂，学生需要具备一定的空间思维和逻辑思维才能推进。笔者通过数形可视化控制条，引导学生观察数形可视化中图形的变化，逐步证明猜想：凸边形的所有内角、外角之和为×180°。即在凸边形中，内角和+外角和=×180°。故，凸多边形外角和为360°。

（二）“正三角形内任意点到三边的距离和等于正三角形的高”的证明

实验：正三角形内任意点到三边的距离和等于正三角形的高。笔者利用Hawgent软件，在直角坐标系中，任意建构一个正三角形，利用函数显示三角形的高，在正三角形中定一个任意点（带坐标），作点到三边的垂线段（用不同颜色表示），利用函数计算出垂线段的距离、、，作对应线段（对应颜色表示）并立于正三角形边上，显示++=，与相等。

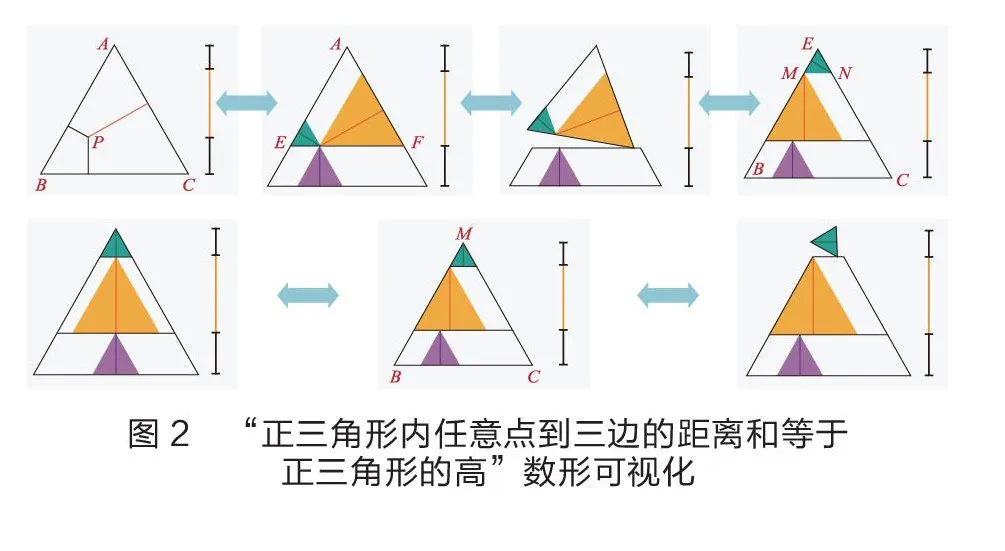
利用Flash制作证明过程动画（循环可逆）。以为顶点，以、、为高，作三个小正三角形，则上面两个小正三角形底边处在同一直线上;过直线切正三角形得正三角形;翻转，把正三角形变为正三角形;同理，翻转把正三角形变为正三角形，将三个小正三角形往中间对齐，其高、、连成正三角形（同：正三角形）的高（如图2）。

通过这样的实验、观察，学生进行猜想，进而得出结论。为了进一步提升学生的理性思维，笔者引导学生对“正三角形的面积始终保持不变，可以得到垂线段的和保持不变”进行证明。

证明1：设正三角形高为，边长为，面积为，为正三角形中任一点，到三边的距离分别为、、，连接、、，得

=S++

故，++。

证明2：设正三角形高为，为正三角形中任一点，到三边的距离分别为、、，过点作平行于底边线段，载得正三角形和等腰梯形，则等腰梯形高为;翻转正三角形，使得点落在正三角形边上（用点表示），过点载得正三角形和等腰梯形，等腰梯形高为，正三角形高为。

正三角形由等腰梯形、等腰梯形、正三角形三部分组成，故，++。

笔者进行数形可视化教学——凸多边形的外角和证明过程可视化、可控可操，高效可逆。在整个证明过程中，避开了烦琐的用大串文字符号证明的过程，将抽象的数学知识高效转变为可控可操作的动画，通过简短的解释说明，高效完成教学任务，提高教学效益。

（三）教学数据统计的数形可视化应用

笔者利用SPSS统计软件，做了一份独立样本检验模板（数据可变），标签为“两组、独立样本、检验”，做了一份配对样本检验模板（数据可变），标签为“两组、配对样本、检验”，入库以供教学之用。学习者或教研者下载模板，填入数据，即可得到检验结果。如此进行数形可视化教学，数据的分析过程可视化、可控可操，高效可逆。教研者并不需掌握SPSS统计软件，亦可从检测结论中判断数据的优劣。

（四）音乐教学的数形可视化

1. 高位置强音演唱技巧（中职学前教育声乐）

笔者利用3DMAX软件，构建腔体发声技巧3D全息系统。笔者设置控制条，配置3D全息魔盒（设备），通过3D旋转多维直观呈现发声时腔体内部结构，使抽象化的发声技巧可视化。学习者边唱边观察，根据歌曲难度，个性化地进行3D全息演示，有效突破课程重难点。对于歌唱腔体发声技巧，笔者通过全息演示实现数形可观化，标签为“歌唱、腔体、发声技巧”，入库，以供学习者模仿感知、理论化归。

例如，歌曲《桑塔露琪亚》需在高位置强音演唱乐句。前面的“快来吧”3个音标有强音演唱记号“>”——表示在演唱时，口腔上口盖充分抬起，舌位放平，留有足够的空间，咬字时，一步到位，不做过多归韵。通过全息模拟，学习者可直观口腔内部结构变化，进而理解专业术语，通过模仿或化归，提高学习效益。

2. 八度音演唱技巧（中职学前教育声乐）

笔者利用动画软件，模拟声音运动轨迹，制作八度音演唱工具，并设计了控制条。笔者用飞机滑翔法和火箭升空法分别呈现抒情性歌唱性强的乐句和欢快跳跃性强的乐句。通过动画控制与演示，现实抽象的声音运动轨迹具体化，可逆转换，高效提升教学效益。例如，用抒情性八度音演唱练习曲。笔者用“飞机滑翔法”，使气息从低音到高音的准备过程可控、可逆、演示，帮助学习者掌握抒情性八度音演唱技巧。以此实现数形可观化，标签为“抒情性、八度音、演唱技巧、飞机滑翔”，入库，以供学习者模仿感知、理论化归（如图3）。

再如，用欢快跳跃性八度音演唱练习曲。笔者利用“火箭法”，使气息从低音（提前准备，快速安放）直冲高音（一步到位）的过程可控、可逆、演示，帮助学习者掌握欢快跳跃性八度音演唱技巧。以此实现数形可观化，标签为“欢快、跳跃、八度音、演唱技巧、火箭”，入库，供学习者模仿感知、理论化归。

数形可视化，可使歌唱过程可视化、具体化、模型化。动画（可逆）演示，代入感强，学生容易效仿，有利于高效掌握演唱技巧。这是一种有效的思维表达方法，但并非所有的知识点都适合采用数形可视化教学。教师应用数形可视化应当以“减负”为出发点，遵从认知规律，牢记两个中心，追求“利、逆、高”发展理念，提高“学与教”的效率。

信息技术高速发展，数与形的分界已经模糊，许多学科都衍变成“数形”综合体，数与形也不再局限于数学学科。在互联网、大数据、人工智能、软件平台的支持下，数形可视化必将成为智能化时代“学与教”的主流思想，其在“学与教”中的应用将更受青睐。笔者在数学与音乐学科中将知识以数形可视化的方法进行了具体化呈现。在教学中，学生更加有效地理解了学科知识的内涵，能够利用相应软件工具进行个人知识的数形可视化表达。借用该思想，在教学中教师应按数形可视化的设计准则与教学实施策略进行教学设计，以数形可视化聚焦教学重点与难点，支撑教师的有效教学与学生的有效理解。总之，数形可视化是一种有效的表达工具和教学方式，也是一种有效培养学生创新性思维的训练模式，对难点知识的呈现有应用价值与研究意义。

参考文献

[1] 马玉武.探究数形结合思想在高中数学教学中的应用[J].中国校外教育，2016（35）：15-16.

[2] 毛雪缘.信息技术背景下小学数学解决问题的教学策略[J].读与写，2020（3）：181.

（作者王统增系广东省东莞市商业学校高级讲师;冯琦系广东省东莞市商业学校讲师）

责任编辑：祝元志