建筑能耗预测的机器学习回归模型研究

2021-12-29李继伟冯国会

沈阳建筑大学学报（自然科学版） 2021年6期

李继伟，冯国会，徐丽

(沈阳建筑大学市政与环境工程学院，辽宁沈阳 110168)

能源消耗是温室气体排放增加和环境污染日益严重的主要原因之一，其中建筑能耗占能源消耗总量的35%以上[1]。20世纪70年代，欧美发达国家就开始了建筑能耗的研究，并制定了建筑节能标准[2-5]。我国的建筑能耗研究起步较晚，且数据缺失严重，因此，国内常用的研究手段主要有现场调研和计算机数值模拟。尤其是到了21世纪大量经典算法的出现，机器学习逐渐被应用于建筑能耗预测或影响因素的研究，如空间关系、建筑材料、环境因素与建筑能耗之间的关系[6-7]，建筑材料、建筑结构、建筑照明和外部气候条件对建筑能耗的影响[8-12]。目前用于建筑能耗预测的机器学习回归模型很多，但是针对建筑能耗预测的回归模型研究鲜有报道。而模型的选择直接影响建筑能耗预测的准确性，因此，笔者以香港地区的商用建筑为研究对象，选取13种常用于预测建筑能耗的回归模型，通过对模型预测性能的比较，获取建筑能耗预测的最优回归模型，为建筑能耗预测和能源供应的合理分配提供技术支持。

1 数据来源与处理

1.1 数据来源

建筑能耗通常受其自身特征、使用性能以及外界环境的影响。笔者采用网络信息收集的方式收集了物理参数、使用参数与环境参数。涉及的建筑样本来源于ESRI网站，该网站提供了1 923个商用建筑样本的能耗数据，具体参数名称与所属类型如表1所示。

表1 参数表Table 1 Features list

表中1-5为建筑的物理参数；6为能源使用指数，即目标参数；7-9为使用参数；10-12为环境参数，其中风环境参数为预处理后的数据。建筑的物理参数和使用参数中的营业时间数据来源于建筑所属的物业公司网站或维基百科，由于其数据来源较为分散，因此数据存在缺失情况，其他使用参数和EUI数据来源于ESRIChina中的香港建筑物能源使用指数网站以及香港民政总署网站，太阳辐射点、制冷度日数数据通过Arcgis和建筑的经纬度坐标计算获得，风环境参数数据来源于香港规划署网站。

1.2 数据预处理

由于参数数值之间差异通常较大，还有个别参数维度较高导致数据冗余，影响拟合过程。因此，笔者在模拟之前对样本数据进行了预处理。数据处理包括风环境参数的降维处理和其他参数的归一化处理两部分。

1.2.1 风环境参数的降维处理

风环境参数数据包含3个高度、16个风向以及24个风速区间参数，共计3×16×24=1 152个数据。笔者采用主成分分析(Principal Component Analysis，PCA)算法，对所有风环境参数进行降维处理。将同高度16×24个风环境参数降维处理为2个参数。常用PCA算法具体步骤：①将参数数据减去同高度参数的平均值，构建矩阵X；②计算矩阵X的协方差矩阵及其特征值和特征向量；③选取2个特征值最大的特征向量，组成特征向量矩阵P；④由步骤①和③构建矩阵Y，即Y=PX。矩阵Y中数据即为降维后的风环境参数。

1.2.2 数据归一化

为了消除各参数间由于数据数量级差异带来的结果误差或不准确，笔者对数据进行了标准化处理。笔者使用的风环境参数数据间由于方差非常小，归一化预处理可以增强数据的稳定性。因此，采用归一化方法对原始数据进行标准化，将各参数数据分别映射到[0，1]之间。

式中：x*为处理后的数据，即原始数据标准化得到的结果；x为原始数据，xmin、xmax为原始数据中最小值和最大值。

2 基于机器学习的能耗预测模型构建

2.1 能耗预测模型

常用于能耗预测的机器学习模型有线性回归、Random Forest、支持向量机、神经网络、梯度提升、k-means、KNN等[8，12-15]，笔者选取13种常见的机器学习回归模型，包括4种基于线性回归的线性模型，2种支持向量机模型，5种基于决策树的集成学习模型，以及其他2种常用回归模型(见表2)。

表2 回归模型列表Table 2 Regressions model list

2.2 模型性能评价指标

为了评价各机器学习回归模型对建筑能耗的预测准确性，笔者选用平均绝对误差MAE、绝对中位差MAD、决定系数 3种性能评价指标对模型进行评价。

MAD=median(|yi-median(y)|).

(3)

式中：n为样本数量;yi为实际EUI值;yi为预测EUI值;y为预测平均EUI值。

MAE和MAD值越小，表明回归模型预测值与实测值的误差越小。R2取值范围为[0，1]，越接近1代表回归模型预测值的离散程度越低。

2.3 样本数据分组

采用StratifiedKFold分层采样法构建机器学习的训练集与测试集，划分比例为8∶2，样本分组结果如表3所示。

表3 样本分组结果Table 3 Result of sample divided

为了保证样本分组后数据结构与总样本集相似，选取总样本、训练集和测试集中的EUI、建筑面积、TPU内人口以及太阳辐射点4项参数的分布情况进行统计分析，验证样本划分的合理性，结果如图1～图4所示。由图1～图4可以看出，总样本、训练集以及验证集中EUI参数分布相似、数值范围一致，建筑面积、TPU内人口以及太阳辐射点3项参数数据分布曲线基本相似。因此，样本划分基本满足机器学习训练的要求。

图1 实测能耗分布Fig.1 Distribution of energy consumption

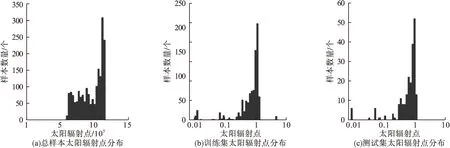
图2 太阳辐射点分布Fig.2 Distribution of point solar radiation

图3 人口数量分布Fig.3 Distribution of population

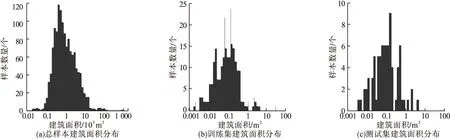
图4 建筑面积分布Fig.4 Distribution of floor area

3 模型验证、分析、优化与应用

3.1 模型验证

根据样本划分的结果，首先采用训练集中样本对13种回归模型进行机器学习训练，然后采用测试集样本对训练好的回归模型进行模型验证和校核，采用式(2)～(4)计算模型各项性能评价指标，具体计算结果如表4所示。从表4可知，基于线性模型的Linear Regression、Ridge Regressor、Lasso、ElasticNet，基于支持向量机的SVR、Linear SVR，基于神经网络的MLP以及基于K近邻学习的KNN回归模型对建筑能耗的预测误差较大，对建筑能耗预测能力较强的Bagging、XGBoost、Random Forest、Extra Trees4种回归模型都属于集成学习，但是集成学习中的AdaBoost回归模型对建筑能耗的预测结果误差很大。其中XGBoost有最小的MAE(6.47)、MAD(2.95)，Random Forest有最大的R2(0.91)。

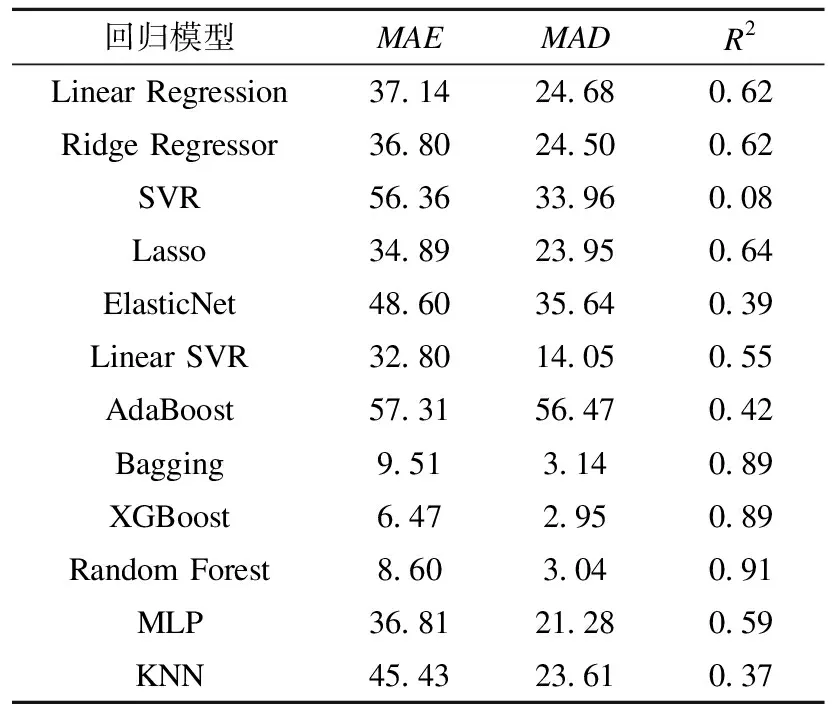
表4 回归模型性能评价指标Table 4 Performance evaluation index of regression

3.2 集成学习回归模型的性能分析

从表4可知，除了AdaBoost回归模型外(见图5)，XGBoost、Bagging、Random Forest、Extra Trees 4种基于集成学习的回归模型性能较好，对EUI的预测较准确(见图6)。实测能耗与预测能耗越接近45°线的点说明预测越准确。

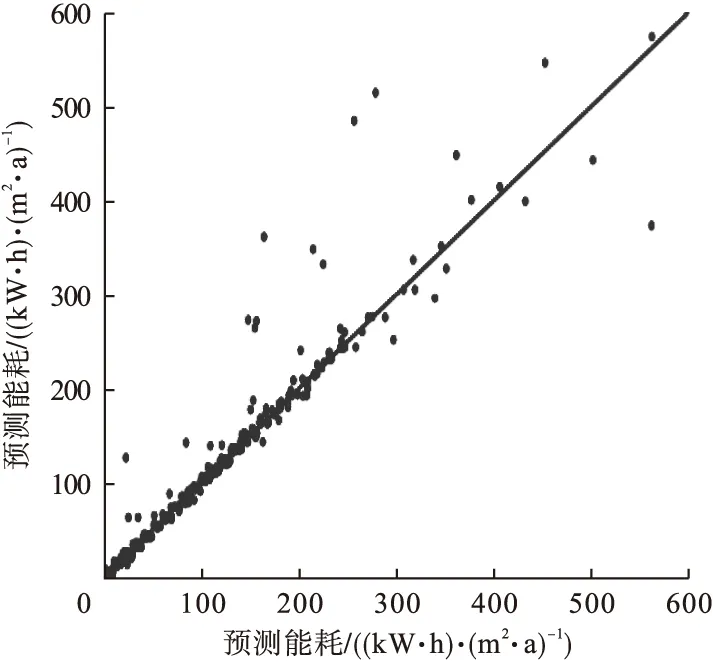
图5 AdaBoost模型预测的能耗分布Fig.5 Distribution of energy consumption predicted by AdaBoost

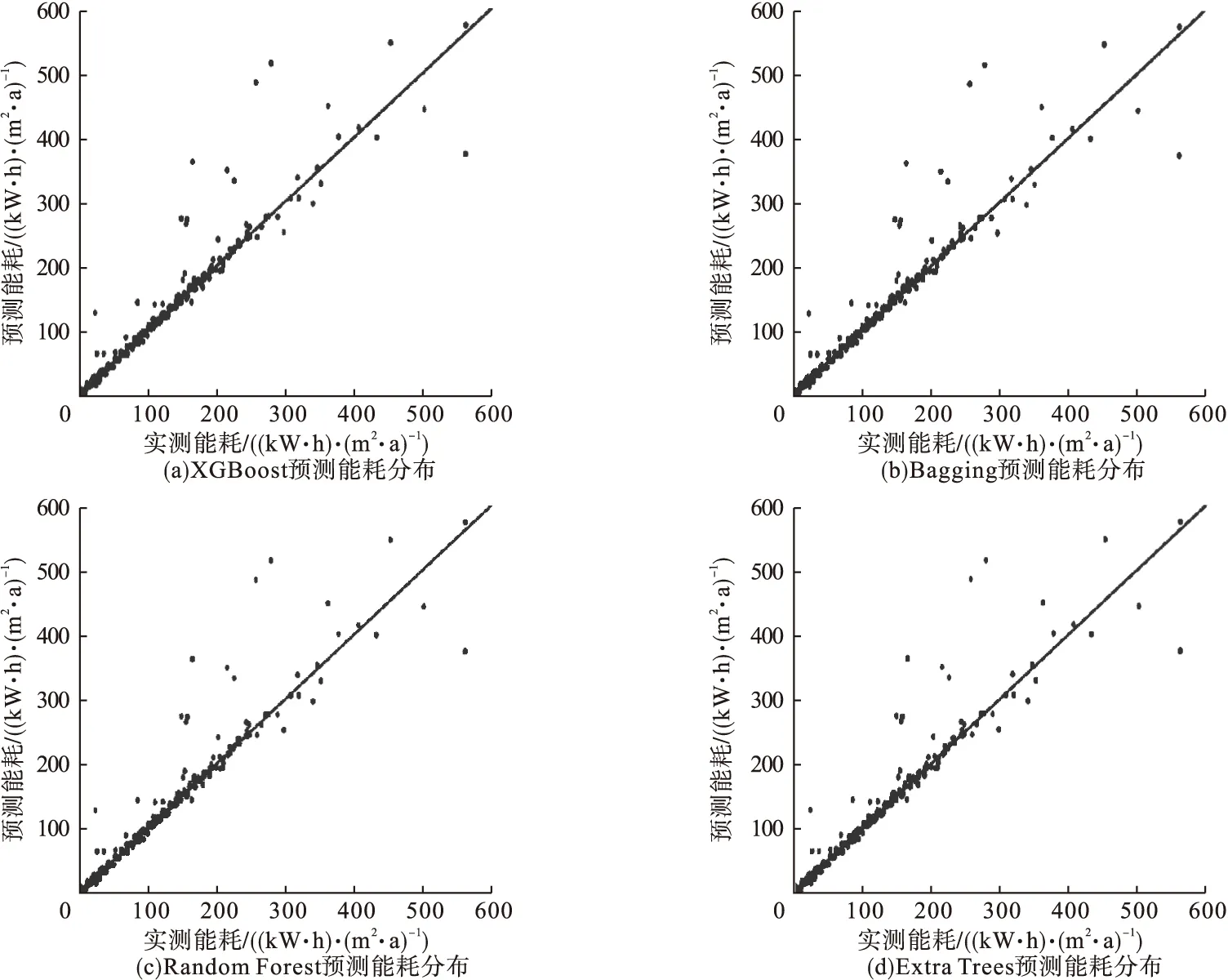
图6 4种回归模型预测能耗分布Fig.6 Distribution of predicted energy consumption by 4 regressors

从图5可知，AdaBoost回归模型预测的能耗与实测能耗误差较大，尤其是实测能耗0～250 (kW·h)/(m2·a)的样本，预测的能耗值主要分布在几条平行于横轴的线附近，实测能耗250～400 (kW·h)/(m2·a)的样本预测较准确，实测能耗大于400 (kW·h)/(m2·a)的样本预测误差较大。AdaBoost回归模型采用改变样本权重的基学习器进行样本分类，然后通过改变错误样本权重的基学习器再次进行样本分类，直至样本分类正确为止，将所有基学习器按分类错误率分配权重，形成建筑能耗预测模型，即此时模拟数据与训练集数据吻合最好。因此，该模型模拟结果依赖于数据质量，而在建筑样本收集过程中，存在不可避免的数据缺失或误差，导致样本在处理过程中存在2种错误情形。第1种情形是原本不属于同一类的样本而被错误的按同一类样本进行处理，从而模糊或降低了样本间的差异，导致样本欠拟合;第2种情形是原本属于同一类型的样本被错误的按不同类型样本进行处理，导致样本过拟合。这两种情形都会导致模拟结果不准确，使得模拟结果高度相似或相等，图5中实测EUI小于250 (kW·h)/(m2·a)的样本被过拟合或欠拟合。

从图6可知，XGBoost对实测能耗低于400(kW·h)/(m2·a)的建筑样本预测基本准确，但是对于实测能耗大于400 (kW·h)/(m2·a)的建筑样本预测误差较大。其余3种回归模型对实测能耗低于300 (kW·h)/(m2·a)的建筑样本预测较为准确，但是少量样本预测的能耗与实际能耗存在误差，预测值偏高，但是对于实测能耗高于300 (kW·h)/(m2·a)的建筑样本，Bagging回归模型预测较为准确，Random Forest回归模型的预测结果更离散，误差更大，Extra Trees回归模型的预测准确性介于两者之间。

这4种模型预测结果优于其他9种模型，其主要原因在于模型自身通过不同的方式避免过拟合的发生，以XGBoost回归模型为例，XGBoost是一种梯度提升回归模型，每一次的训练都是在残差减小的方向上建立模型，模型中有专门控制精度项和防止过拟合项，同时还考虑了数据的缺失情况。其数学函数为

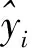
Bagging和Random Forest两种回归模型都是对所有建筑样本进行多次有放回的随机抽样构建训练样本集，每次抽样的数量与表3中训练集样本数量相同。每个基学习器训练的样本不同，最终的预测能耗取所有训练结果的算术平均值。由于噪声数据占比低，因此大部分基学习器的训练结果基于正确数据，降低了噪声数据对预测结果的影响，相比于AdaBoost回归模型可以更有效地避免噪声数据的干扰。Extra Trees中训练集是总样本，所有基学习器训练的样本相同，都是总样本，因此，高能耗样本比Random Forest的训练更充分，样本的预测结果更准确且离散程度更低(见图6(b)～图6(d))。

3.3 模型优化

选取MAE、MAD两项性能评价指标较小且R2较大的回归模型进行参数调整，进一步提高回归模型对建筑能耗预测的准确性。调参之后4种回归模型的性能评价指标数值如表5所示。

表5 调参后性能评价指标Table 5 Performance evaluation index after features adjustment

从表4和表5可知，除Random Forest外，调参后各算法的3项性能评价指标都优于调参前，说明调参后模型精度更好，预测能力更强，XGBoost依然是4种回归模型中预测最准确的回归模型。

3.4 模型应用

在42项样本参数的基础上构建模型，而实际工作中，收集完整的42项参数数据很难实现，而有些参数对能耗的影响可以忽略，仅需收集影响较大的参数，因此，需分析42项参数的重要性。由于Random Forest回归模型的基学习器中任意节点的分裂取决于样本的参数重要性，即节点增益，计算所有基学习器中相同参数的节点增益，就可以获取各项参数在建筑能耗中的重要性。所以，笔者采用Random Forest回归模型进行了参数重要性分析。

通过Random Forest回归模型筛选出权重之和接近0.95的参数共有7项，建筑面积、建筑独立性、风环境参数、出租状态、太阳辐射点、建筑高度以及层数，对应的权重分别为0.67、0.16、0.05、0.044、0.01、0.01、0.01。基于这7项参数，采用4种优化后模型预测了所有建筑样本能耗，结果如图7所示，各模型的性能如表6所示。

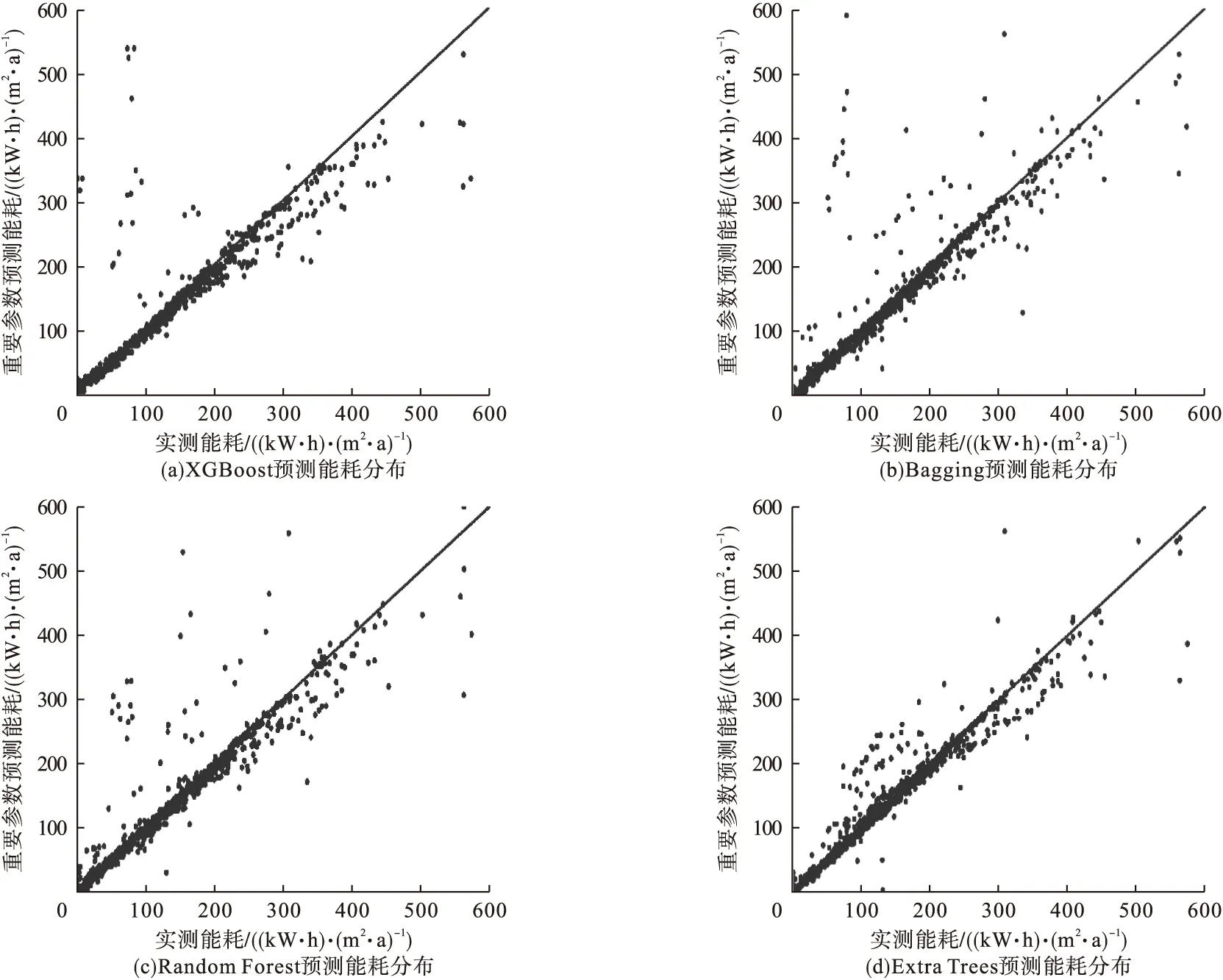
图7 基于重要参数的预测能耗分布Fig.7 Distribution of predicted energy consumption by important features

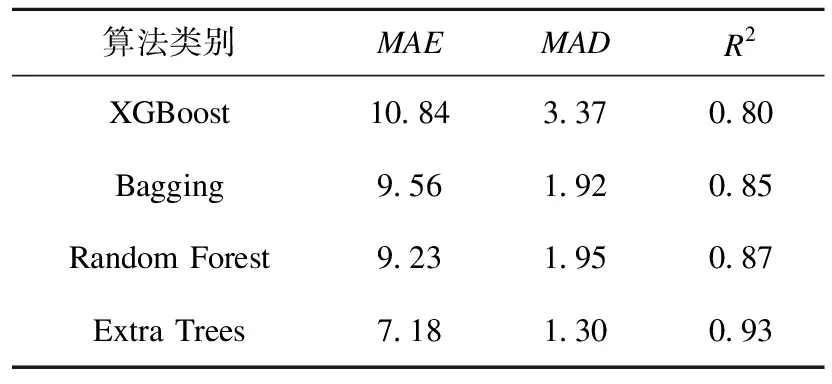
表6 基于7项参数的模型性能Table 6 Performance of models by 7 features

由表6可以看出，Bagging、XGBoost、Random Forest、Extra Trees4种回归模型性能评价指标较好，其中Extra Trees的3项性能评价指标皆为最优，说明在参数不全或数据缺失的情况下，这4种回归模型仍可以有效预测建筑能耗。图7中预测能耗基本与实测能耗一致，误差在可接受范围内。与图6相比，7项参数能耗预测结果和42项参数预测结果分布情况相似，基本一致，进一步说明这4种回归模型均可用于建筑能耗预测。