陆上风机基础混凝土的可靠度分析

陆征然，马梦梦，郭 超

(1.沈阳建筑大学管理学院，辽宁 沈阳 110168；2.沈阳建筑大学土木工程学院，辽宁 沈阳 110168)

风力发电机属于新型高耸结构，其风机基础不仅要承受机身自身的重力荷载，也长期承受着作用在塔筒和叶片上的风荷载，而风荷载作为分布极其不规律的随机荷载，会导致风机基础面临很多疲劳破坏问题，且风机基础混凝土疲劳损坏的累积，将会使风机出现摇摆，停机的情况。因此，对于风机基础进行混凝土疲劳可靠度的研究就显得极为重要。

目前有很多学者对风机结构进行了研究：周新刚等[1]采用有限元方法分析了正常荷载和极端荷载下风机基础的受力特点，找出了风机基础被破坏的主要原因；S.Bisoi等[2]使用风和波浪载荷作用下的有限元模型进行计算和分析，发现基础混凝土出现裂纹的主要影响因素是疲劳载荷；霍涛[3]以气象站记录的数据为基础，研究了风速风向对风机疲劳寿命的影响；李炜等[4]对海上风电基础进行有限元模拟，依据线性累积损伤理论，研究了不同疲劳荷载情况下海上风电基础的损伤程度；汪宏伟[5]讨论了采用混凝土环梁加固风机基础的可行性；迟洪明等[6]针对陆上风机基础存在的承台裂缝、基础环溢浆等问题，提出了灌浆处理的加固方法。

尽管国内外学者对风机基础开展了较多的理论分析，但大都采用对风机整体结构简化、仅对风机基础建立精细化模型进行分析的方式，与实际情况相差较多，且针对风机基础疲劳可靠度问题进行优化的较少。基于此，笔者利用通用有限元软件ABAQUS建立1.5 MW陆地风电机整体有限元模型，基于Davenport谱模拟脉动风速时程，指数模型模拟平均风速时程，把求得的风荷载施加于模型上，用于提取风机基础危险部位的应力时程；结合概率密度演化方法，计算风机基础混凝土的疲劳可靠度，并且通过有限元模拟结果与风机基础混凝土疲劳可靠度的变化规律，对风机基础提出了优化设计。研究表明：风机在运行过程中，发生混凝土疲劳破坏的概率是不能忽视的，在基础环上增加栓钉抗剪连接件能显著改善风机基础混凝土的疲劳可靠度，是陆地重力式风电基础抗疲劳的关键构件。

1 风荷载模拟与疲劳可靠度的理论概述

1.1 风速与风荷载的数值模拟

沿着风向的风速时程包括平均风速与脉动风速两部分。平均风速的周期较长，其周期时间大于10 min。脉动风速的周期很短，只有几秒到几十秒。风机结构上任意高度的合成风速按(1)计算。

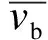
采用Davenport谱[8]模拟脉动风速时程，风谱采用谐波叠加法，由MATLAB软件编程计算。作用于叶轮上的风荷载用推力系数法[9]计算：

F=0.5ρaπr2v3CT.

(3)

式中：ρa为空气密度，取1.277 kg /m3；r为叶轮半径；v为风速；CT为推力系数，该值为风机厂商提供。

作用在塔筒上的风荷载为

式中：ρ为空气密度，其值取1.277 kg /m3;CD为阻力系数；塔筒的阻力系数取1.2；v为风速；A为塔筒在不同高度处的投影面积。

1.2 基础混凝土的疲劳损伤计算理论

损伤是指在长期重复荷载作用下材料的损坏程度，一般用一个无量纲参数D来表示。当D=0时，说明材料完好无损；当D>1时，表示材料失效。风机的混凝土基础在使用过程中承受的循环荷载为高周疲劳荷载，因此笔者选取雨流计数法[10]统计该循环荷载下应力均值和应力幅值所对应的循环次数，S-N曲线计算对应应力水平下的循环次数，结合Palmgren-Miner[11]线性疲劳损伤准则计算总的损伤值D，其表达式为

式中：ni为等效应力对应的频次；Ni为S-N曲线应力S对应下的寿命。

本节计算混凝土疲劳时采用混凝土抗压疲劳方程[12]：

式中：Smax为风荷载作用下的应力水平，MPa；Nf为对应应力水平下发生的疲劳破坏循环次数。

1.3 基础混凝土的疲劳可靠度求解方法

根据概率密度演化方法[13]的基本思想，对于混凝土疲劳损伤D，可以构造一个虚拟随机过程，使待求随机变量成为该虚拟随机过程的截口随机变量。就结构动力学问题而言，疲劳损伤值D必须依赖于随机参数θ，构造以τ为虚拟时间参数的虚拟随机过程Zl[14]:

Zl=D(θ,T)·τ.

(7)

显然D(θ,T)为Zl在τ=1时截口随机变量，即:

D(θ,T)=Zl|τ=1.

(8)

(Zl,Θ)的联合概率密度函数pzlΘ(z,θ,τ)的概率密度演化方程为

其初始条件为

PZlΘ(z,θ,τ)|τ=0=δ(z)pΘ(θ).

(10)

求解偏微分方程初值问题(9)、(10)即可给出联合概率密度函数pzlΘ(z,θ,τ)，进而给出Zl(τ)的概率密度函数:

由式(8)可知：

pD(D)=pzl(z,τ)|z=D,τ=1.

(12)

由式(12)即可得随机结构的可靠度，即：

(13)

方程(9)的得出来源于概率密度演化思想[13]，并由随机结构的动力反应控制方程确定初始条件后经过推导得出，在计算方程(9)时，令θ=θq,θq=θ1,q,…,θs,q，将对应θq的D(θq,T)代入该方程中，可得联合概率密度函数pZlΘ(z,θq,τ)，进而对方程(11)积分并结合式(12)和(13)，最终可得D值的疲劳可靠度。在这个过程中，概率密度pΘ(θq)是确定的，θq是通过动力学方程[14]在已知初始条件下进行求解得到的，在式(9)中，将θq代入到θ，D(θq,T)代入到D(θ,T)，在式(10)的初始条件下，通过单边差分法得到离散值pZlΘ(zj,θq,τm)，在此计算中zj=jΔz(j=0，1，…)，其中Δz是空间步长，τm=m·Δτ(m=0，1，…，N)，Δτ是时间步长，对式(12)进行数值积分，便会得到风机基础疲劳可靠性概率密度的数值解。

2 实例计算

2.1 风机有限元模型建立

笔者选取山东某地区额定功率为1.5 MW的近海风机，风机由混凝土基础、基础环、塔筒、叶片和机舱5部分组成，其中叶轮、机舱和发电机的总质量为91.2 t，风机轮毂总高度为92 m，塔筒总高度为90 m，由三段变截面的塔筒组成。在ABAQUS有限元软件中进行建模，底部基础为C35混凝土，塔筒和基础环都采用理想弹塑性的Q345E钢材，风机叶片采用玻璃纤维树脂CFRP材料。将塔底设置为全约束边界条件，塔筒与塔顶质量块、叶片与机舱、基础环与塔筒连接处采用tie绑定，混凝土基础与基础环进行通用接触(General Contact)。风机整体模型的网格划分如图1所示。

图1 风机整体网格划分图Fig.1 Overall grid division of wind turbine

2.2 风荷载的计算

基于Davenport谱和谐波叠加法，采用MATLAB分别对脉动风速与合成风速进行模拟。N取1 000，频率上限wu取20 Hz，频率下限wk取0 Hz;因计算较危险工况下的疲劳可靠度，而轮毂在8级风的状态下，即对应风速为17.2～20.7 m/s时，工作情况比较危险，由平均风速的指数模型(2)计算可得标准参考高度下的平均风v10=12 m/s。

由于是近海风机，a取0.12，模拟时间步长为0.1 s，模拟总时长取300 s。为了验证Davenport谱模拟风速的准确性，笔者选取 15 m处的模拟谱和目标谱，以及在平均风为14.5 m/s时，实测的风速数据与模拟谱模拟的风速进行对比，结果如图2～图3所示。

图2 模拟谱与目标谱的对比图Fig.2 Comparison of simulated spectrum and target spectrum

图3 模拟风速与实际风速对比Fig.3 Comparison of simulated wind speed and field wind speed

由图2和图3可知，文中Davenport的计算谱以目标谱为中线，在其两侧有较小的浮动，基本符合了目标谱的曲线规律，且模拟风速与实测风速趋势大体一致，可以由此确定Davenport谱模拟脉动风速的正确性。故可将平均风速与脉动风速按照1.1小结理论合成，结合MATLAB软件进行编程，分别计算作用于塔筒和叶片上的风荷载。

2.3 有限元计算结果与分析

2.3.1 风机基础混凝土疲劳可靠度

将风荷载施加在风机有限元模型上，即可以得到风机基础的动力响应。任意时刻的基础混凝土应力云图其应力最大的位置相同，只是应力大小变化的数值有所区别。现取某一时刻基础混凝土的等效应力云图如图4所示，从图中可以找出基础的危险部位。

图4 风荷载作用下的基础剖面图Fig.4 Section of foundation under wind load

从图4可以看出：风荷载作用下，应力值最大的位置为基础环内外侧与混凝土基础表面接触处，故此处为疲劳危险位置，符合实际工况的破坏位置。现提取混凝土处危险点的应力时程，所得应力时程曲线如图5所示,该应力时程的雨流统计数据如图6～图7所示。

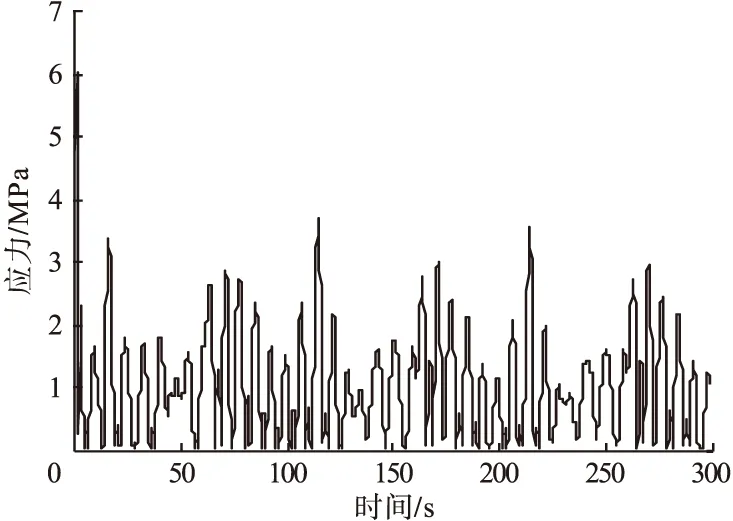
图5 危险点的应力时程Fig.5 Stress time history of dangerous points

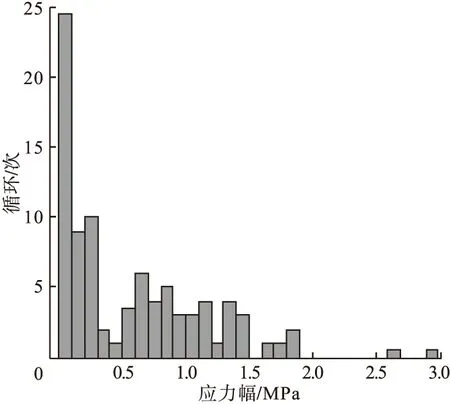
图6 应力幅对应循环次数Fig.6 Number of cycles corresponding to stress amplitude

图7 平均应力对应循环次数Fig.7 Number of cycles corresponding to average stress

把上述得到的雨流计数结果进行等效应力修正，结合笔者选取的混凝土S-N曲线对提取的应力时程根据线性叠加理论进行疲劳损伤计算，可得到加载时长在300 s下的疲劳损伤值为3.7×10-7，把上述求得的结果以秒为单位进行转化，将之与10～30年的加载时长相乘,即可得到对应年限下的混凝土疲劳损伤累积值，将上述求得的不同年限下的疲劳损伤值进行离散化处理，且采用单边差分法对计算方程(9)求解，在计算中，时间步数取100，步长0.005 s，疲劳的离散步数取50步，离散区间为[1,5]，代入上述求得的疲劳损伤值,可得到同一风速下不同年限的疲劳损伤概率密度迭代结果如图8所示。

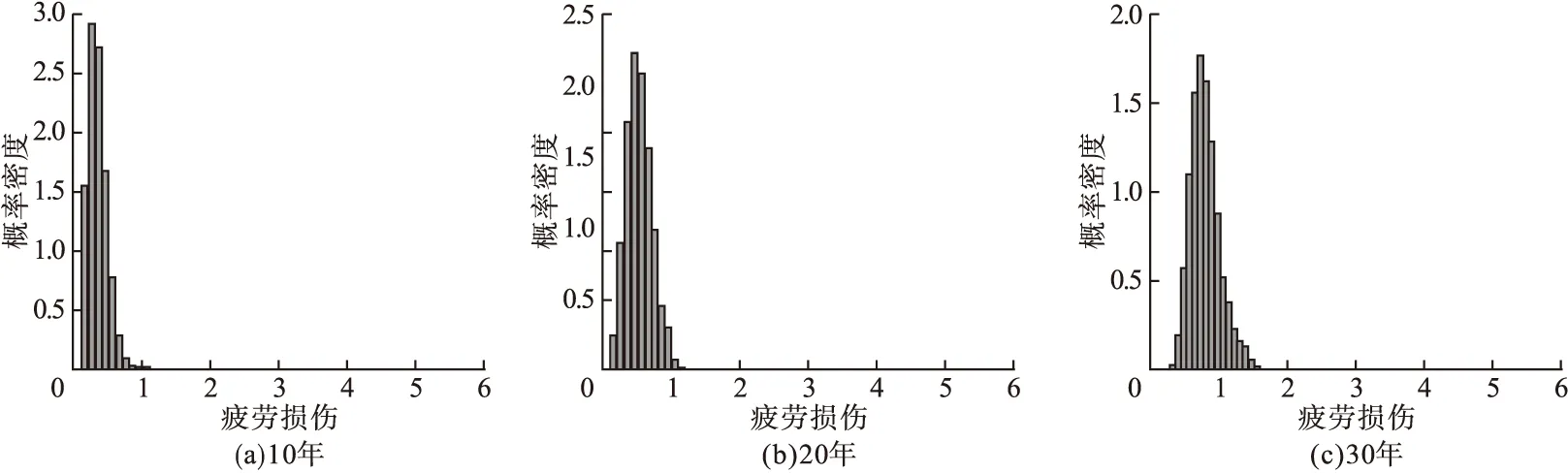
图8 10～30年的概率密度迭代结果Fig.8 Iterative results of probability density for 10～30 years

由图8可看出，随着使用年限的增加，混凝土疲劳损伤值低于1的累计概率逐渐减少，同时，概率密度曲线向大于1的方向偏移。将某一年限下混凝土疲劳损伤值低于1的部分进行积分，与其全部概率密度进行相比，即可得到不同年限下结构的可靠度，计算结果如图9所示。

图9 混凝土疲劳可靠度Fig.9 Fatigue reliability of concrete

由图9可知，混凝土疲劳可靠度随着使用年限的增长不断下降，且使用年限与降低速度呈正相关。当使用期限为10年时，其疲劳可靠度为98.45%，则破坏概率有1.55%；当使用年限为20年时，其疲劳可靠度为93.32%，则破坏概率有6.68%，从而表明了风机在运行过程中，发生基础混凝土疲劳破坏的概率还是不能忽视的。

2.3.2 基础环的位移分析

在ABAQUS中使用接触后，即可输出从面上节点与主面的距离(Copen)，用u表示，有限元模拟结果如图10所示。由图可以看出风机基础环与混凝土之间会出现脱开现象。提取基础环与混凝土之间脱开距离随着时间变化的曲线(见图11)。由图11可以看出，在施加时长300 s的风荷载作用下，其最大脱开距离可达8 cm。

图10 风荷载作用下基础环与混凝土的脱开距离Fig.10 Separation distance between foundation ring and concrete under wind load

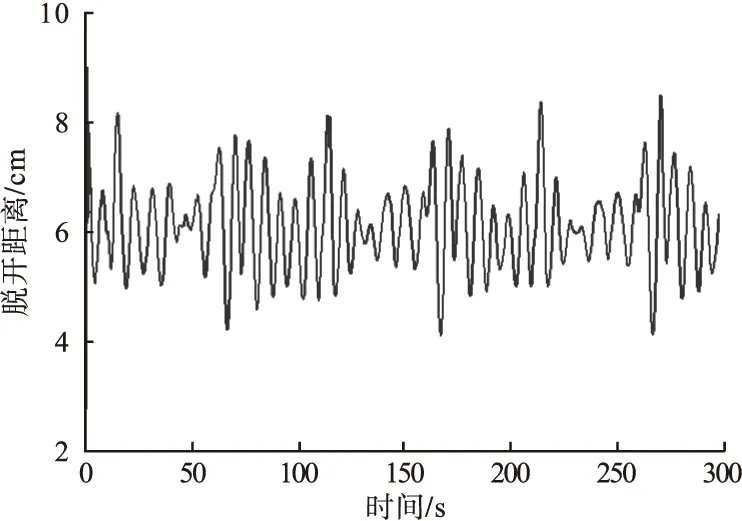
图11 基础环和混凝土脱开距离的时程曲线Fig.11 Time history curve of separation distance between foundation ring and concrete

3 优化设计

3.1 优化有限元模型的建立

针对以上对风机基础的分析，为了增强风机基础的可靠度，需要考虑在基础环表面采取加强措施。参考组合梁抗剪连接件推出的实验结论[15]，且考虑优化后的结构形式要便于混凝土的捣实，笔者将在基础环外圈上下两层加焊栓钉，作为抗剪连接件来提高基础环和混凝土接触界面的粘结作用。栓钉直径为25 mm，长300 mm，抗拉强度为400 MPa，屈服强度320 MPa，弹性模量取206 GPa，泊松比取0.3。基础环优化的有限元模型如图12所示。

图12 基础环优化模型的网格划分Fig.12 Mesh model and grid generation of foundation ring

3.2 优化效果

3.2.1 优化后的疲劳可靠度

利用前述方法，可得到优化后风机基础的动力响应，现取某一时刻基础混凝土的等效应力云图如图13所示,其危险部位的应力时程曲线如图14所示。

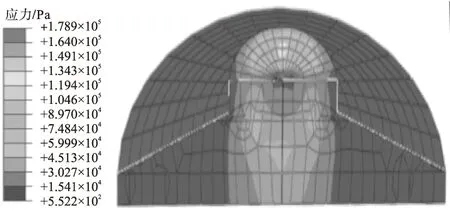
图13 风荷载作用下的优化基础剖面图Fig.13 Optimal foundation profile under wind load

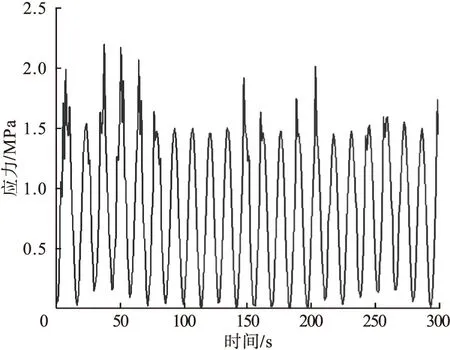
图14 危险点的应力时程Fig.14 Stress time history of dangerous points

将上述应力时程曲线按照前述方法进行计算，可得到优化后的风机基础在加载时长为300 s时所造成的疲劳损伤，其值为1.142×10-7，由此求得10～30年的疲劳损伤累积值，并且进行概率密度迭代，结果如图15所示。

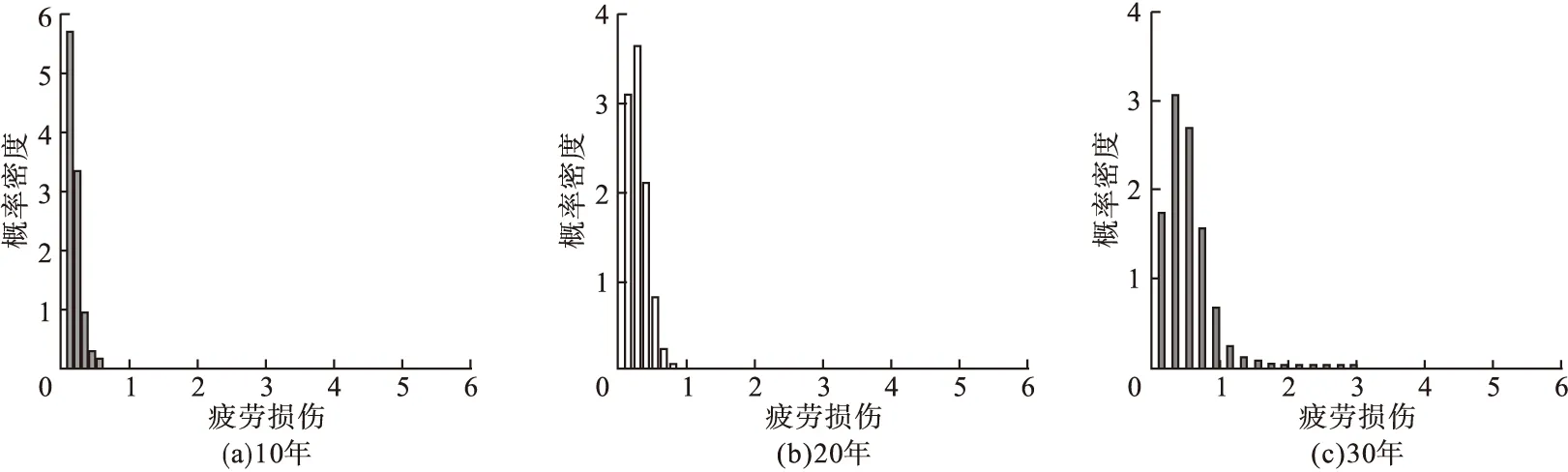
图15 10～30年的概率密度迭代结果Fig.15 Iterative results of probability density for 10～30 years

由图15可看出，与未优化前相比，同样年限下混凝土疲劳损伤值低于1的累计概率分布更多。按照前述方法，即可得到不同年限下优化结构的可靠度，计算结果如图16所示。

由图16可知，当使用年限为20年时，混凝土疲劳可靠度为98.22%，则破坏概率有1.78%，较未优化前的疲劳可靠度提高了5%，说明风机基础加入栓钉后可以有效地提高风机基础的疲劳可靠度。

3.2.2 风机基础的滞回曲线对比

有限元计算中，在基础顶部选一参考点RP-1，并与基础环上表面建立运动耦合约束(kinematic coupling)，在参考点处施加20 mm的往复位移荷载，提取优化前、后风机基础的荷载-位移曲线进行对比(见图17)。

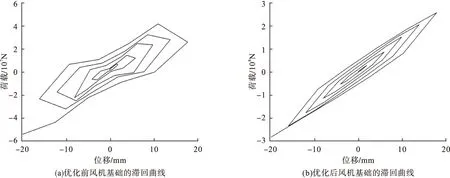
图17 两个风机基础结构的滞回曲线Fig.17 Hysteretic curves of two wind turbine foundation structures

由图17可看出，当对两个风机基础施加同样的位移荷载时，未优化风机基础抵抗位移荷载时的最大反力为6.0×104kN，优化后风机基础抵抗位移荷载时的最大反力为3.0×105kN，同样位移荷载作用下较优化前反力增大了4倍，且优化后风机模型滞回曲线的形状比优化前的更加饱满，说明加有栓钉后风机基础的塑性变形能力和耗能能力明显更强，从而风机基础的疲劳可靠度也会随之提高。

4 结 论

(1)将10～30年的混凝土疲劳损伤值作为概率密度演化的初始条件，代入一维对流方程中，对疲劳损伤值小于1的概率密度进行积分，可以得到风机基础混凝土的可靠度数值。

(2)由计算结果可以看出，随着使用年限的增加，混凝土疲劳可靠度不断降低，当使用年限为20年时，其疲劳可靠度有93.32%，则破坏概率为6.68%，从而表明了风机在运行过程中，发生疲劳破坏的概率还是不能忽视的。

(3)由图10和图11可以看出，风机底部基础环与混凝土之间会出现脱开现象，在施加时长300 s的风荷载作用下，其最大脱开距离可达8 cm，是影响风机基础承载性能的重要环节。

(4)荷载和基础尺寸参数相同情况下，在基础环上增加栓钉抗剪连接件不但能够将基础环滞回曲线反力峰值提高4倍，还可以使得风机基础混凝土的疲劳可靠度提高，使其能够有效抵抗疲劳振动荷载作用，是陆地重力式风电基础抗疲劳的关键构件。