理解“归一问题”中的数量关系
2021-12-29□胡琼
□胡 琼
四年级学生在数学学习中会遇到“归一问题”。解决这类问题的核心要素是理解数量关系。以下教学活动可以帮助学生理解“归一问题”中的数量关系。
一、提出问题,唤醒数量关系
教师出示题目部分信息“用100千克大豆可以榨出13千克豆油”,引导学生思考:根据这个信息你能提出哪些数学问题?学生提问后师生共同整理大家提出的问题并进行简单分类。
问题1:每千克大豆可以榨出多少千克豆油?
问题2:200千克(300千克、1000千克……)大豆可以榨出多少千克豆油?
问题3:每榨出1千克豆油需要多少千克大豆?
……
教师请学生分析问题1和问题2的异同,引导学生发现问题1是问题2的基础,也就是说要求若干千克大豆榨油的数量,就要回归到求出每千克大豆榨多少油。教师小结,这类需要先解决“1”是多少才能继续求得答案的问题可以称之为“归一问题”。
二、多元表征,揭示数量关系
1.多元表征,尝试解决
呈现完整题目:“用100千克大豆可以榨出13千克豆油。1吨大豆可以榨出多少吨豆油?”请学生画一画、写一写,用喜欢的方式表示题中信息,并整理自己的思路。
2.展示交流,理清思路
教师呈现学生的典型表征(如图1~图4),引导学生思考:你能理解每幅图表示的意思吗?图4的第一段表示什么?这些表征方法有什么共同点?学生通过交流发现,这几幅图用了不同的表征方法,有用箭头、列表、画圆圈或线段图等,但每种方法都简洁地提取了题目中的关键信息。

图1
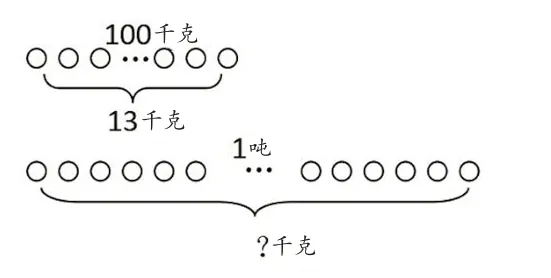
图2

图3
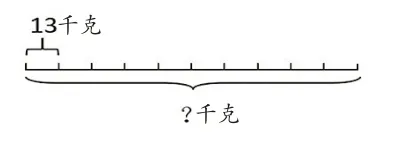
图4
三、深度思考,梳理数量关系
1.对比异同
请学生进一步思考:4幅图在问题解决的思路上有什么异同?通过交流引导学生发现4幅图都表达了“归一”的思路,都是先求每份数,再求总数,但所取的“1”不同。其中,图1和图2的每份数是每千克,先求出每千克大豆可以榨出0.13千克豆油,再用0.13×1000求出这样的1000份可以榨油130千克。图3和图4则是把100千克看作一份大豆,因为1吨里面有这样的10个100千克,所以1吨大豆能榨油的数量是10个13千克,也就是130千克。
2.梳理关系
教师根据学生的交流,结合板书梳理各信息之间纵向和横向的关系(如图5)。
纵向看:由13对应100可知1千克大豆可榨出0.13千克豆油;130对应1000也就是1千克大豆对应0.13千克豆油,这里的“1”是指每千克为1份。
横向看:把100千克看作“1”,1000千克是“1”的10倍,那么13的10倍就是130。
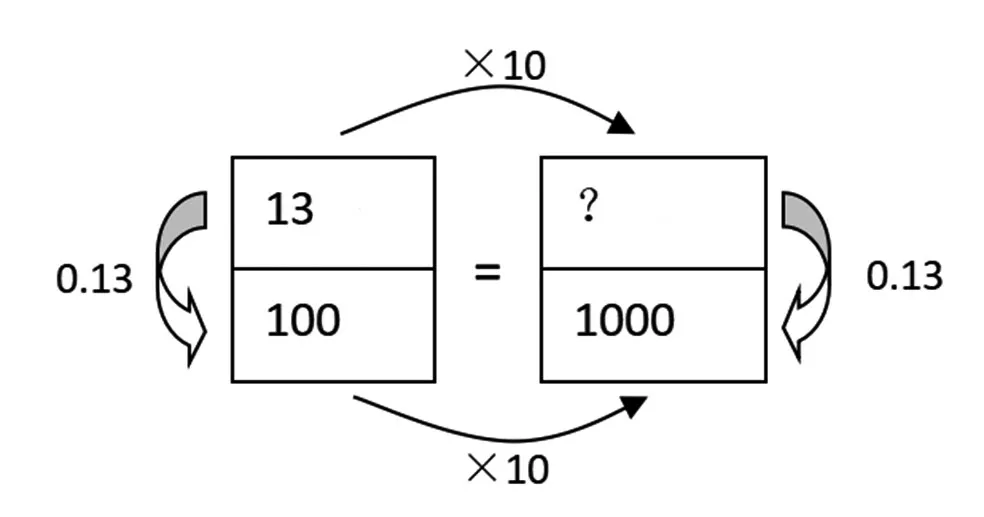
图5
如上,学生经历想、画、写、说等活动,借助文字表征、表格表征、图形表征等方式,不仅理解和掌握了数量关系,还有效地提升了建模能力和问题解决能力。
