基于分形维数特征的砂滤层适宜粒径范围
2021-12-29李景海翟国亮刘清霞蔡九茂
李景海,翟国亮,刘清霞,宋 蕾,蔡九茂
基于分形维数特征的砂滤层适宜粒径范围
李景海1,2,翟国亮1,刘清霞2※,宋 蕾1,蔡九茂1
(1. 中国农业科学院农田灌溉研究所/河南省节水农业重点实验室,新乡 453002;2. 安阳工学院土木与建筑工程学院,安阳 455000)
为了对砂滤层过滤性能进行分析,该研究以粒径范围为1.0~1.18、>1.18~1.4和>1.4~1.7 mm的3种砂滤层为研究对象,以黄河泥沙作为原水杂质颗粒,采用激光衍射粒度分析仪测量了人民胜利渠泥沙粒度分布,得到了泥沙粒度分布的密度函数,并以兰考县黄河泥沙对泥沙粒度分布规律进行了验证。采用工业CT对3种砂滤层进行扫描,利用计算机图像处理技术,采用像素点覆盖法,自编程序计算了3种砂滤层横截面特征参数,孔隙率均值分别为0.421、0.431和0.439,计盒分形维数均值分别为1.695、1.709和1.726,截面最小孔径与最大孔径比分别为1/17、1/18和1/21,拟合了孔隙率与计盒分形维数的相关关系,分析了砂滤层分形理论适用性。建立了砂滤层过滤概率分形模型,计算了3种砂滤层孔隙直径范围,分别为59.5~1 002、66.9~1 220和72.9~1 503m,计算了原水中100m以上杂质颗粒通过砂滤层的概率,对于人民胜利渠泥沙,分别为0.67%、0.81%和0.93%,对于兰考县黄河泥沙,分别为0.62%、0.80%和0.91%。从理论上证明了表层过滤的存在性,分析了表层过滤的机理及其对反冲洗频率的影响。同时,为了减轻表层过滤,粒径范围为>1.4~1.7 mm的滤层更适宜作为砂过滤器的滤料。研究可为砂滤层内部结构的研究和滤料选型提供基础理论与数据参考。
泥沙;粒径;图像处理;石英砂滤层;表层过滤;过滤性能;计盒维数
0 引 言
砂过滤器是微灌系统中普遍使用的过滤器之一[1],为了提高砂过滤器的过滤性能,不少学者进行了相关研究。20世纪90年代,董文楚[2-3]提出砂滤层主要通过机械筛滤、沉淀和接触絮凝作用去除水中的杂质,为砂滤层机理研究奠定了基础。在试验方面,翟国亮等[4-5]对自制粉煤灰水进行过滤和反冲洗试验,分析了滤后水和反冲洗水浊度和杂质颗粒质量分数的变化规律;张杰武等[6]以自制黄河水为原水,对砂滤层过滤性能进行了测试。在数值模拟方面,李景海等[7-9]对滤层反冲洗过程进行了动态模拟,通过对流场分析确定了砂滤层的合理反冲洗速度范围。在滤料形貌特性方面,刘清霞等[10-11]基于图像处理技术,计算了砂颗粒等效直径、简化延长指数和布拉斯谢克系数,采用统计分析方法对砂颗粒粗糙度参数进行了分析,为砂滤层细观结构分析提供了基础理论与方法。在过滤效果与过滤介质选型方面,Godwin等[12]对用于改善废水水质的砂滤层的最佳床层厚度和有效尺寸进行了研究。Wolff等[13]对利用下游砂过滤器去除污水中的微塑料进行了研究。Chan等[14]对活性碳法和砂过滤法的水质强化效果进行了比较。Xia等[15]利用砂壤土和砂土为介质,对含砂水进行过滤,并对过滤效果进行了分析。杜加法等[16]对矿山充填尾砂过滤脱水性能进行了研究。Ibrahim等[17]将砂滤层中混合其他介质,研究其过滤性能,并选出最佳滤料组合。Saini等[18]将植物修复与砂过滤结合进行废水处理,效果良好。Li等[19]采用砂滤法对煤气化废水中细颗粒污染进行去除,去除率95%以上,分离精度0.46m。综上可知,目前对砂过滤的研究,主要侧重于从宏观上分析过滤和反冲洗效果,而基于滤层内部结构对过滤效果的研究较少。砂滤层内部结构决定了滤层孔隙大小及其分布规律,直接关系到原水中哪些粒径的杂质能被过滤及其被滤除的比率。对砂滤层细观结构特性的研究,为从机理层面研究砂滤层过滤性能提供了前提条件。
砂滤层内部颗粒的排列与孔隙分布具有随机性,要从理论上精确描述这种不规则性和随机性,分形理论具有天然的优势。将分形理论应用于砂过滤器的研究,可以从细观层面研究砂滤层孔隙结构及其分布规律,从机理上分析砂滤层过滤性能,这方面的研究目前仅见李景海等[20]采用分形理论建立了砂滤层清洁压降的分形阻力模型,并探讨了滤层最佳过滤速度的计算方法。而在相关领域,有不少对分形理论的应用[21-23],其成果为砂过滤器的研究提供了理论和方法上的借鉴。
笔者在前期的研究中[24-25],以西北地区普遍采用的粒径范围为1.0~1.18、>1.18~1.4和>1.4~1.7 mm的3种砂滤层为研究对象,采用激光衍射粒度分析仪对黄河泥沙粒度特征进行测量,确定黄河泥沙粒度分布的密度函数。采用工业CT扫描技术对砂滤层进行扫描,利用计算机图像处理技术,采用像素点覆盖法,自编程序计算砂滤层横截面孔隙率、计盒分形维数和截面最小孔径与最大孔径比值,在此基础上,拟合孔隙率与计盒分形维数的相关关系,对砂滤层分形理论适用性进行分析。建立滤层过滤概率分形模型,对过滤效果进行分析,从理论上证明表层过滤的存在性,以期为微灌砂滤层内部结构的研究和滤料选型提供基础理论与方法参考。
1 材料与方法
1.1 砂滤层扫描与泥沙样本粒度测量
为了获得砂滤层自然堆积状态下的横截面,分别将粒径范围为1.0~1.18、>1.18~1.4和>1.4~1.7 mm石英砂滤料盛入容积为600 mL、直径为95 mm的烧杯中,采用工业CT扫描设备(C16M3201,洛阳腾达检测服务有限公司)对滤料样本进行立体扫描,从扫描结果中截取滤层横截面(示例如图1),每种滤层随机截取3个横截面。
由人民胜利渠采集黄河泥沙样本,样本数为7。由兰考县黄河段采集黄河泥沙,样本数为1。使用激光衍射粒度分析仪(Mastersizer 3000,丹东百特仪器有限公司)采用湿法对所采集的2种黄河泥沙样本粒度分布进行测量,得到不同粒度颗粒的体积占比。
1.2 砂滤层横截面计盒分形维数计算方法
维空间中,由边长为的小立方体平铺组成的坐标网立方体[26]定义为
[1,(1+1)]×…×[mδ,(m+1)] (1)
式中为坐标网立方体边长;[mδ,(m+1)]为坐标网立方体的边;m(1,2,…,)为整数。
设是中的任意一个非空有界子集,用N()表示集合与坐标网立方体相交的个数。则集合的计盒分形维数dimB为
二维计盒分形维数用格子边长为的正方形网格对分形体进行覆盖,得到与分形体相交的非空网格数N,逐步改变网格的边长,得到一系列N。二维计盒分形维数表示为
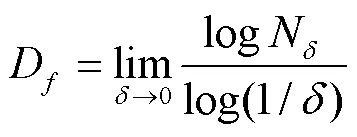
式中D为二维计盒分形维数,一般介于1~2之间,如果二维计盒分形维数不在该范围内,说明砂滤层横截面孔隙分布或砂颗粒分布不具有分形特征[27]。
根据式(3),将每次划分所得的非空格子数N与对应的网格边长在双对数直线坐标下进行直线拟合,所得拟合直线斜率的绝对值即为二维计盒分形维数,该方法为像素点覆盖法[22],计算流程见图2。
1.3 砂滤层分形理论适用性判别方法
对多孔介质,孔隙分布的概率密度函数[28]为
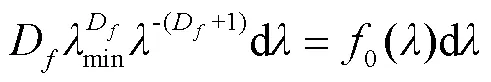
式中min为最小孔隙直径,mm;为孔隙直径,mm。
显然,概率密度函数应满足归一化条件,如下:
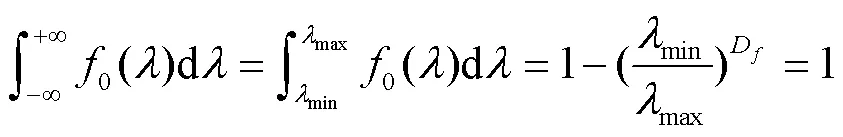
式中max为最大孔隙直径,mm。
因此,多孔介质是否适用分形理论的判断依据为
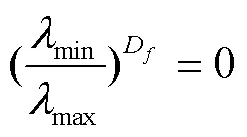
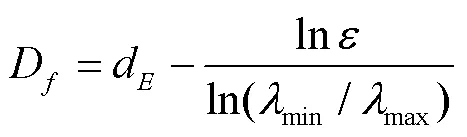
式中为截面孔隙率;d为欧式空间维数,石英砂滤层横截面为二维空间,因此d取2。
1.4 砂滤层过滤概率分形模型
由式(4)知,滤层截面孔径为的孔隙的分布密度为
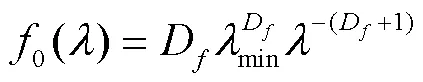
则孔径小于的孔隙的占比为
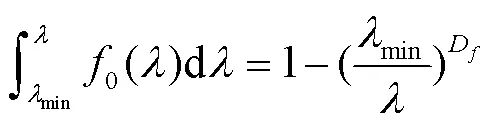
则滤层截面孔径大于的孔隙占比为
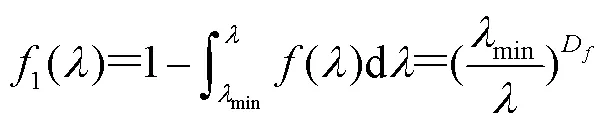
设原水中泥沙粒度分布的概率密度函数为(),则粒径为的颗粒通过滤层的概率为
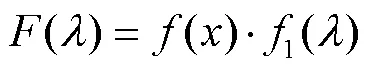
式中为泥沙粒径,m。
根据多孔介质理论,max的表达式[30]为
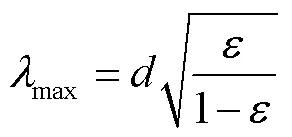
式中为砂滤层颗粒最大粒径,m。
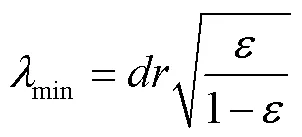
在滴灌带中,粒径小于100m的杂质颗粒不会引起滴灌带的堵塞[32]。因此,砂滤层只需要滤除原水中粒径大于100m的杂质,则粒径大于100m的杂质颗粒通过砂滤层的概率为
式(10)~式(14)联立,得到砂滤层过滤概率分形模型。
2 结果与分析
2.1 砂滤层横截面分形参数计算结果分析
从每种滤层中随机截取3个横截面,自编程序对截面图像进行处理。首先,对图像进行二值化处理,将图像中砂颗粒所包含的像素点标为0,其余像素点标为1。其次,将横截面用小网格划分,网格边长δ分别为1、2、4、8、16个像素,在图2中对应的的预设值分别为288、144、72、36、18。数出网格总数N,将横截面周长与周长上像素点个数相比,可计算单个像素边长(1.21m),对每种划分方法,计算网格边长;数出含有像素1的网格的数目N,计算结果见表1。
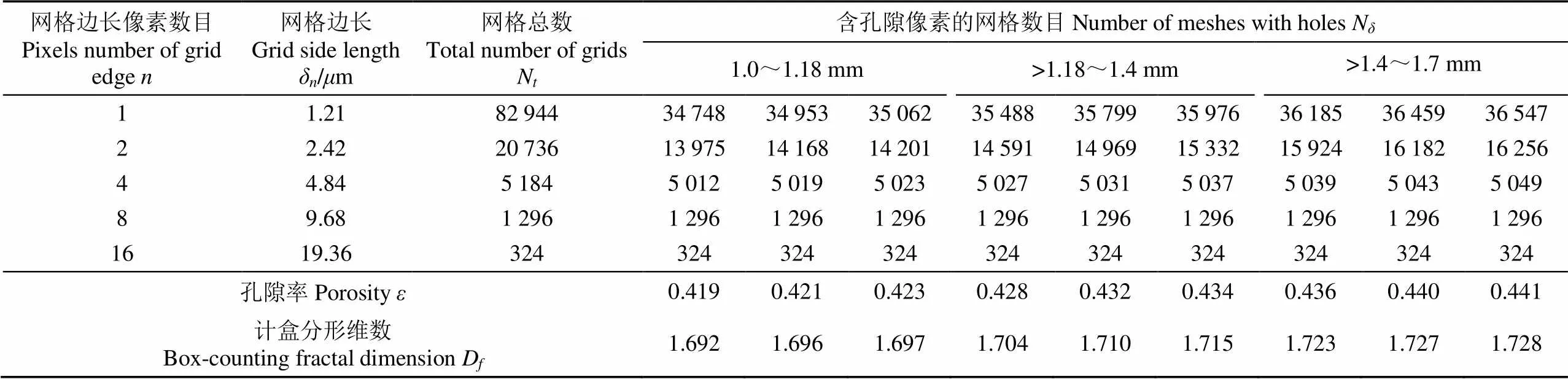
表1 滤层截面图像处理结果
滤层截面孔隙率为滤层截面孔隙处像素的数目N与截面网格总数N的比值,即
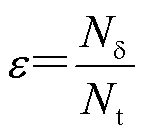
由式(15)可得滤层截面孔隙率,结果见表1。由表1知,粒径范围为1.0~1.18 mm的滤层所对应的3个截面孔隙率分别为0.419、0.421和0.423,均值为0.421;粒径范围为>1.18~1.4 mm的滤层所对应的3个截面孔隙率分别为0.428、0.432和0.434,均值为0.431;粒径范围为>1.4~1.7 mm的滤层所对应的3个截面孔隙率分别为0.436、0.440和0.441,均值为0.439。
根据图像计盒分形维数的像素点覆盖法,将(δ,N)绘入双对数坐标系,用最小二乘法拟合得到网格数目与网格边长之间的线性关系曲线,曲线斜率即为滤层截面孔隙的计盒分形维数。由表1知,粒径范围为1.0~1.18 mm的滤层所对应的3个截面的计盒分形维数分别为1.692、1.696和1.697,均值为1.695;粒径范围为>1.18~1.4 mm的滤层所对应的3个截面的计盒分形维数分别为1.704、1.710和1.715,均值为1.709;粒径范围为>1.4~1.7 mm的滤层所对应的3个截面的计盒分形维数分别为1.723、1.727和1.728,均值为1.726。
2.2 滤层横截面孔隙分布规律与分形理论适用性分析
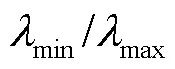
2.3 计盒分形维数与孔隙率的相关性分析
绘制滤层截面孔隙率与滤层截面孔隙计盒分形维数的倒数1/D之间的散点图(图3),拟合得到滤层截面孔隙率与截面孔隙计盒分形维数D之间的经验关系,由图3知,截面孔隙率与截面孔隙计盒分形维数D之间相关性较高,决定系数2为0.980 9。
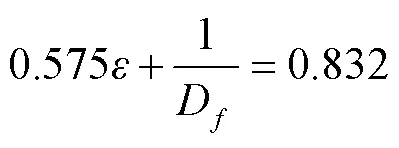
由式(16)知,截面孔隙率与滤层孔隙计盒分形维数D具有相同的变化趋势,孔隙率增加,计盒分形维数随之增加;孔隙率减小,计盒分形维数随之减小。
孔隙率可以通过注水法[25]测出。在孔隙率已知的情况下,由式(16)可计算出截面计盒分形维数,结果见表2。与像素点覆盖法相比,粒径范围为1.0~1.18、>1.18~1.4和>1.4~1.7 mm的3种砂滤层截面计盒分形维数计算误差分别为0.01%、0.21%和0.65%,最大误差仅0.65%。
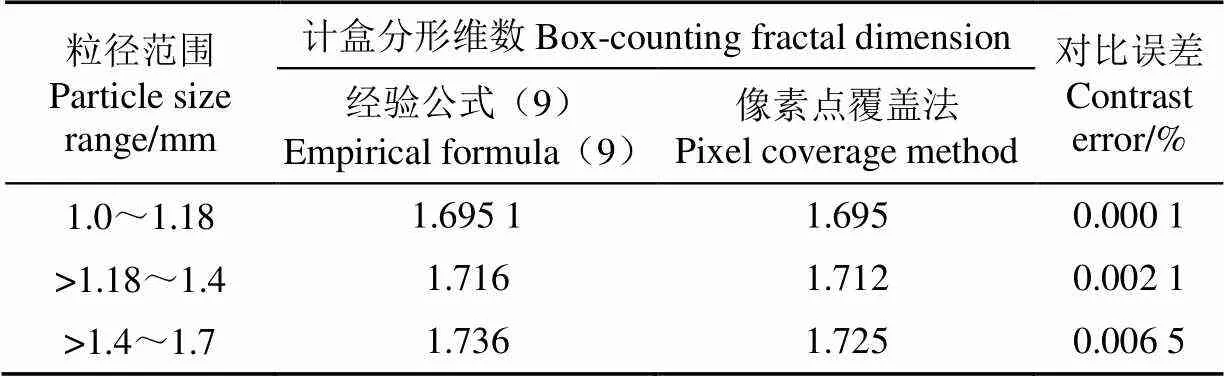
表2 计盒分形维数经验公式法与像素覆盖法计算结果对比
2.4 黄河泥沙粒度分布特征分析
根据激光衍射粒度分析仪测量结果,得到人民胜利渠与兰考县段黄河泥沙粒度频率分布图(图4,其中人民胜利渠泥沙以样本7示例),并计算样本粒度均值、标准差、偏度和峰度。其中,样本偏度为样本3阶标准矩,样本峰度为样本4阶标准矩[31]减3,黄河泥沙样本参数计算结果见表3。
正态分布的偏度和峰度均为0,将原水泥沙样本参数与正态分布对比,可以判断泥沙分布是否为正态分布。由表3知,人民胜利渠泥沙样本的偏度最大值0.27,最小值为-0.05,均值为0.12,标准差为0.14,偏度的分值为0.84;样本峰度最大值0.79,最小值为-1.01,均值为-0.01,标准差为0.56,峰度的分值为0.018。当检验水平为0.05时,分布检验的()为1.96,显然偏度与峰度的分值均小于(),泥沙样本分布为正态分布。兰考县黄河泥沙偏度为-0.11,峰度为-0.23,均接近0。由此可知,人民胜利渠与兰考县泥沙样本均来自于正态分布的总体,泥沙粒度分布的概率密度函数可表示为
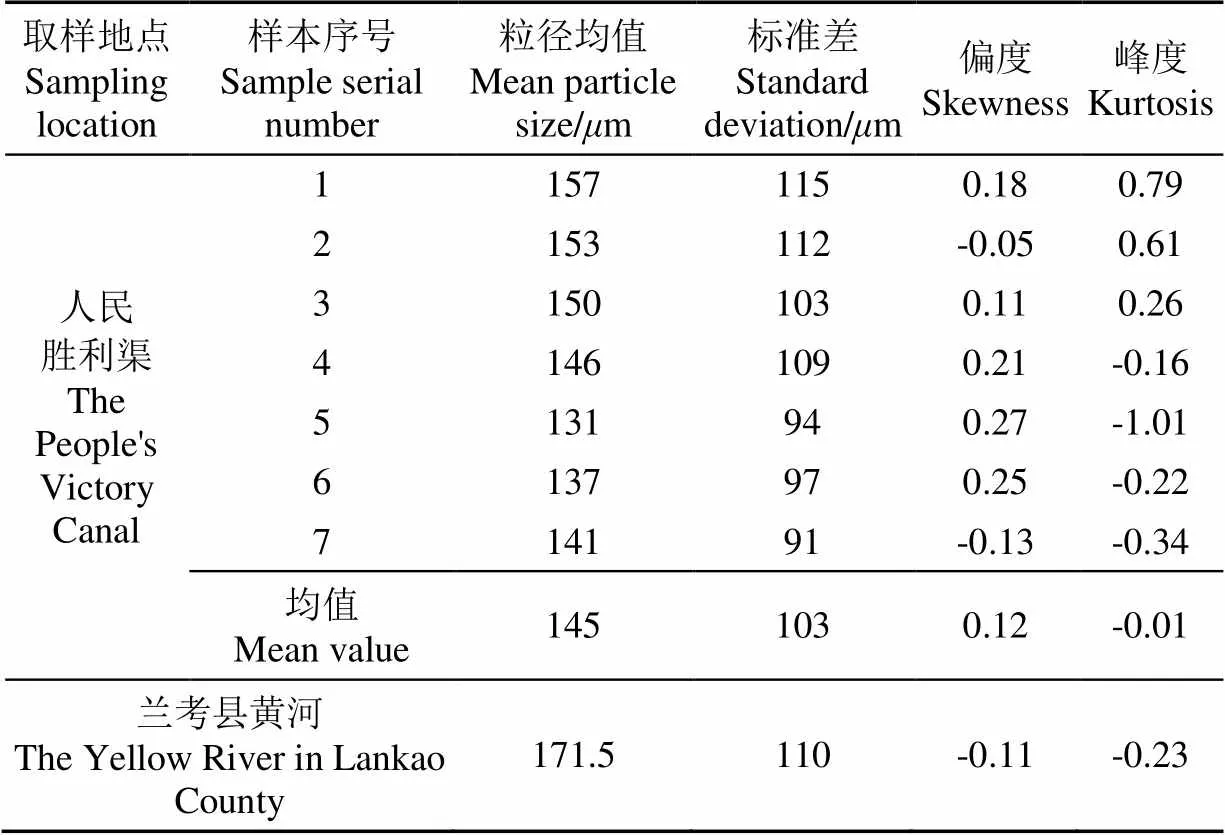
表3 黄河泥沙样本参数计算结果
由式(12)~式(14)和式(17)可计算出3种滤层最大孔径max、最小孔径min和粒径大于100m的杂质颗粒通过砂滤层的概率(),见表4。
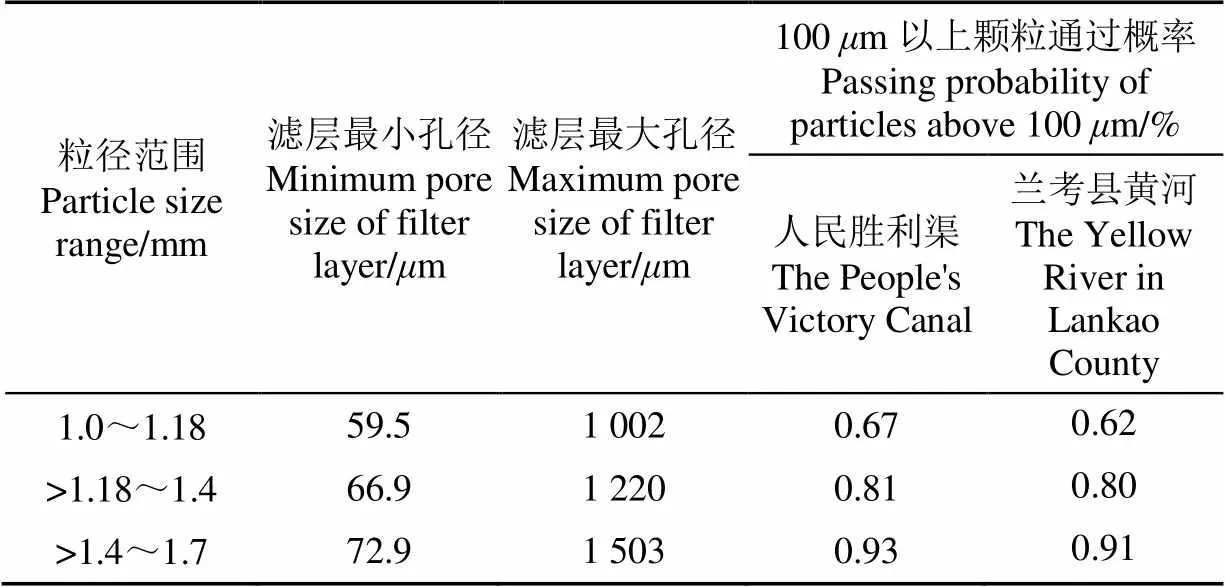
表4 滤层参数计算结果
由表4知,粒径范围为1.0~1.18、>1.18~1.4和>1.4~1.7 mm的3种砂滤层孔隙直径范围分别为59.5~1 002、66.9~1 220和72.9~1 503m,对于人民胜利渠泥沙,100m以上杂质颗粒通过砂滤层的概率分别为0.67%、0.81%和0.93%,对于兰考县黄河泥沙,100m以上杂质颗粒通过砂滤层的概率分别为0.62%、0.80%和0.91%。结果表明,砂滤层截面孔径范围比较大,但对杂质的过滤能力极强,100m以上杂质颗粒通过的概率不到1%,说明砂过滤器几乎能够将黄河泥沙中易于造成堵塞的杂质全部滤除。
由图4知,人民胜利渠泥沙和兰考县黄河泥沙中100m以上杂质颗粒占比均达到60%以上,砂滤层截面高效的过滤能力,使原水中的泥沙大部分截留到了滤层表面,当大的杂质颗粒累积到一定程度,造成滤层表面孔隙直径的进一步减小,从而使小的杂质颗粒也在滤层表面迅速累积,导致了严重的表层过滤现象。而表层过滤由于表面颗粒堆积较快,堵塞也加快,影响滤速,同时增加了反冲洗次数,造成反冲洗用水的浪费和过滤效率降低。显然,在3种滤料中,粒径范围为>1.4~1.7 mm的滤层表层过滤现象相对轻微,更适宜作为砂过滤器的滤料。
3 结 论
1)采用工业CT技术,对粒径范围为1.0~1.18、>1.18~1.4和>1.4~1.7 mm的3种砂滤层进行扫描,得到滤层横截面图像。在此基础上,采用像素点覆盖法,自编程序计算了滤层截面孔隙率和孔隙计盒分形维数,3种滤层截面孔隙率均值分别为0.421、0.431和0.439,孔隙计盒分形维数均值分别为1.695、1.709和1.726,并拟合了孔隙率与计盒分形维数的相关关系。根据截面计盒分形维数和孔隙率,计算了截面孔径比,分析了砂滤层分形理论适用性。
2)采用激光衍射粒度分析仪对人民胜利渠和兰考县黄河泥沙样本进行测量,得到黄河泥沙粒度频率分布,计算得到人民胜利渠黄河泥沙样本偏度和峰度均值分别为0.12与-0.01,兰考县黄河泥沙样本偏度和峰度分别为-0.11与-0.23,显著性水平为0.05时,泥沙样本符合正态分布,从而得到泥沙粒度分布的概率密度函数。
3)建立了砂滤层过滤概率分形模型,根据砂滤层过滤概率分形模型,得到了3种砂滤层孔隙直径范围分别为59.5~1 002、66.9~1 220和72.9~1 503m,对于人民胜利渠泥沙,100m以上杂质颗粒通过砂滤层的概率分别为0.67%、0.81%和0.93%,对于兰考县黄河泥沙,100m以上杂质颗粒通过砂滤层的概率分别为0.62%、0.80%和0.91%。结果表明,原水中的泥沙大部分截留到了滤层表面,导致表层过滤现象严重。为了减轻表层过滤现象,粒径范围为>1.4~1.7 mm的滤层更适宜作为砂过滤器的滤料。
砂滤层横截面孔隙分布具有随机性,不同滤层高度的截面,孔隙率和截面分形维数存在一定差别,本文仅研究了滤层表面的过滤性能,而没有考虑滤层截面孔隙特征随滤层高度的变化规律及过滤效果随截面位置的变化规律,因此研究结论存在一定误差,未来需进一步研究。
[1] Duranros M. Effect of filter, emitter and location on clogging when using effluents[J]. Agricultural Water Management, 2009, 96(1): 67-79.
[2] 董文楚. 微灌用过滤砂料选择与参数测定[J]. 喷灌技术,1995(2):42-46.
Dong Wenchu. The material selection and parameter determination of sand filter in micro irrigation[J]. Sprinkler Irrigation Technology, 1995(2): 42-46. (in Chinese with English abstract)
[3] 董文楚. 微灌用砂过滤器堵塞与反冲洗效果研究[J]. 武汉水利电力大学学报,1996,29(6):30-34.
Dong Wenchu. Study on the Clogging and backflushing coefficient of the sand filters for micro-irrigation[J]. Journal of Wuhan University of Hydraulic and Electric Engineering, 1996, 29(6): 30-34. (in Chinese with English abstract)
[4] 翟国亮,陈刚,赵红书,等. 微灌用均质砂滤料过滤粉煤灰水时对颗粒质量分数与浊度的影响[J]. 农业工程学报,2010,26(12):13-18.
Zhai Guoliang, Chen Gang, Zhao Hongshu, et al. Effects of filter with uniform sandy filtration medium used in micro-irrigation on mass fraction of particles and turbidity of water with fly ash[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(12): 13-18. (in Chinese with English abstract)
[5] 翟国亮,冯俊杰,邓忠,等. 微灌用砂石过滤器反冲洗参数试验[J]. 水资源与水工程学报,2007,18(1):24-28.
Zhai Guoliang, Feng Junjie, Deng Zhong, et al. Parameters experiment of backwashing on sandy filter in micro-irrigation[J]. Journal of Water Resources & Water Engineering, 2007, 18(1): 24-28. (in Chinese with English abstract)
[6] 张杰武,冯吉,徐飞鹏,等. 引黄滴灌砂石过滤器滤料过滤性能[J]. 排灌机械工程学报,2016,34(4):357-361.
Zhang Jiewu, Feng Ji, Xu Feipeng, et al. Sand filter performance on drip irrigation with the Yellow River[J]. Journal of drainage and irrigation machinery engineering, 2016, 34(4): 357-361. (in Chinese with English abstract)
[7] 李景海,翟国亮,黄修桥,等. 微灌石英砂过滤器反冲洗数值模拟与流场分析[J]. 农业工程学报,2016,32(9):74-82.
Li Jinghai, Zhai Guoliang, Huang Xiuqiao, et al. Numerical simulation and flow field analysis of backwashing of Quartz sand filter in micro irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(9): 74-82. (in Chinese with English abstract)
[8] 李景海,蔡九茂,翟国亮,等. 基于砂滤层内水体积分数瞬态模拟的反冲洗速度优选[J]. 农业工程学报,2018,34(2):83-89.
Li Jinghai, Cai Jiumao, Zhai Guoliang, et al. Optimization of backwashing speed based on transient simulation of the volume fraction of water in the sand filter layer[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(2): 83-89. (in Chinese with English abstract)
[9] 李景海,刘清霞,翟国亮,等. 基于颗粒流理论的微灌砂滤层反冲洗过程砂粒速度场模拟[J]. 农业工程学报,2018,34(22):78-83.
Li Jinghai, Liu Qingxia, Zhai Guoliang, et al. Numerical simulation of velocity field of sand grains in backwashing process of sand filter layer in micro-irrigation based on granular flows theory[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(22): 78-83. (in Chinese with English abstract)
[10] 刘清霞,李国强,李景海,等. 基于图像处理技术的微灌砂颗粒形状参数分析[J]. 节水灌溉,2019(11):66-70.
Liu Qingxia, Li Guoqiang, Li Jinghai, et al. Analysis of shape parameters of sand particles in micro-irrigation based on image processing technology[J]. Water Saving Irrigation, 2019(11): 66-70. (in Chinese with English abstract)
[11] 刘清霞,李国强,李景海,等. 微灌砂过滤器石英砂滤料颗粒粗糙度参数测算与分析[J]. 中国农村水利水电,2020(1):1-6.
Liu Qingxia, Li Guoqiang, Li Jinghai, et al. Measurement and analysis of roughness parameters of quartz sand particles for sand filters in micro-irrigation[J]. China Rural Water and Hydropower, 2020(1): 1-6. (in Chinese with English abstract)
[12] Godwin K N, Peace K A, Samuel A, et al. Optimal bed thickness and effective size for improving wastewater quality for irrigation[J]. International Journal of Energy and Environmental Engineering, 2020(11): 1-16.
[13] Wolff S, Weber F, Kerpen J, et al. Elimination of microplastics by downstream sand filters in wastewater treatment[J]. Water, 2020, 13(1): 33-39.
[14] Chan M R A A, Kasmuri N, Ahmad R, et al. Comparison between activated carbon and sand filtration method for water quality enhancement: A case study [J]. IOP Conference Series: Earth and Environmental Science, 2021, 646(1): 1-7.
[15] Xia T, Tian J C, Fei W P. Experimental study on the performance of a sand filtration method and device by using natural soils and subsurface PVC drainage pipes[J]. Journal of Irrigation and Drainage Engineering, 2021, 147(4): 1-7.
[16] 杜加法,宋泽普. 矿山充填尾砂过滤脱水性能试验研究[J]. 有色金属,2021,73(3):6-9. Du Jiafa, Song Zepu. Experimental research on filtration dewatering performance of backfilling tailings in mine[J]. Nonferrous Metals, 2021, 73(3): 6-9. (in Chinese with English abstract)
[17] Ibrahim K A I, Sabry T I M, El G A S, et al. The efficiency of the sand filtration unit mixed with different packing materials in drain water treatment in Egypt[J]. Applied Water Science, 2021, 11(6): 23-28.
[18] Saini G, Kalra S, Kaur U. The purification of wastewater on a small scale by using plants and sand filter[J]. Applied Water Science, 2021, 11(4): 45-52.
[19] Li D, Hualin W. Removal of Solid Impurities from Coal Gasification Wastewater by Sand Filtration[J]. E3S Web of Conferences, 2021, 241: 1001-1011.
[20] 李景海,刘清霞,黄修桥,等. 微灌石英砂滤层流态特性与分形阻力模型参数确定[J]. 农业工程学报,2015,31(13):113-119.
Li Jinghai, Liu Qingxia, Huang Xiuqiao, et al. Flow state characteristics and fractal model parameters determination of quartz sand filter layer used in micro-irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(13): 113-119. (in Chinese with English abstract)
[21] 崔建江,贾旭,刘晶,等. 基于计盒维数和多小波的静脉图像特征提取[J]. 东北大学学报:自然科学版,2010,31(10):1397-1400.
Cui Jianjiang, Jia Xu, Liu Jing. Vein image feature extraction based on box counting dimension and multiple wavelets[J]. Journal of Northeastern University: Natural Science, 2010, 31(10): 1397-1400. (in Chinese with English abstract)
[22] 冯志刚,周宏伟. 图像的分形维数计算方法及其应用[J]. 江苏理工大学学报,2001,22(6):92-95.
Feng Zhigang, Zhou Hongwei. Computing method of fractal dimension of image and its application[J]. Journal of Jiangsu University of Science and Technology, 2001, 22(6): 92-95. (in Chinese with English abstract)
[23] 田玉强,李新,江明喜. 后河自然保护区珍稀濒危植物种群分布格局的分形特征:计盒维数[J]. 应用生态学报,2003,14(5):681-684.
Tian Yuqiang, Li Xin, Jiang Mingxi. Fractal properties of the spatial pattern of rare and endangered plant populations in Houhe Nature Reserve in Hubei: Box-counting dimension[J]. Chinese Journal of Applied Ecology, 2003, 14(5): 681-684. (in Chinese with English abstract)
[24] 李景海. 微灌石英砂滤层清洁压降分形阻力模型与反冲洗数值模拟[D]. 北京:中国农业科学院,2016.
Li Jinghai. Fractal Resistance Model of Clean Pressure Drop and Numerical Simulation of Backwashing Process of Quartz Sand Filter Layer in Micro-Irrigation[D]. Beijing: Chinese Academy of Agricultural Sciences, 2016. (in Chinese with English abstract)
[25] 李景海,翟国亮,刘清霞,等. 基于Ergun方程的微灌砂颗粒形状系数测定方法研究[J]. 节水灌溉,2020(12):1-5.
Li Jinghai, Zhai Guoliang, Liu Qingxia, et al. Study on the method of determination of the shape coefficient of sand particle in micro-irrigation based on Ergun equation[J]. Water Saving Irrigation, 2020(12): 1-5. (in Chinese with English abstract)
[26] 法尔科内. 分形几何:数学基础及其应用(曾文曲译)[M].北京:人民邮电出版社,2007,39-41.
[27] 郁伯铭. 多孔介质输运性质的分形分析研究进展[J]. 力学进展,2003,33(3):333-346.
Yu Boming. Advances of fractal analysis of transport properties for porous media[J]. Advances in Mechanics, 2003, 33(3): 333-346. (in Chinese with English abstract)
[28] Chen Y P, Shi M H. Determintion of effective thermalconductivity for real porous media using fractal theory [J]. Thermal Science, 1999, 8(2): 102-107.
[29] Yu B M, Li J H. Some fractal characters of porous media[J]. Fractals, 2001, 9(3): 365-372.
[30] Wu J S, Yu B M. A fractal resistance model for flow through porous media[J]. International Journal Heat and Transfer, 2007, 50(6): 3925-3932.
[31] 田禹. 基于偏度和峰度的正态性检验[D]. 上海:上海交通大学,2012.
Tian Yu. Tests for Normality Based on Skewness and Kurtosis[D]. Shanghai: Shanghai Jiao Tong University, 2012. (in Chinese with English abstract)
[32] 赵红书,微灌用石英砂滤料的过滤与反冲洗性能研究[D]. 北京:中国农业科学研究院,2010.
Zhao Hongshu. Performance of Filtration and Flushing of Quartz Sand Media for Micro-Irrigation[D]. Beijing: Chinese Academy of Agricultural Sciences, 2010. (in Chinese with English abstract)
Suitable particle size range of sand filter layers based on fractal dimension characteristics
Li Jinghai1,2, Zhai Guoliang1, Liu Qingxia2※, Song Lei1, Cai Jiumao1
(1.,-,453002,; 2.,,455000,)
This study aims to evaluate the filtration performance of sand filters using fractal dimensions. Three kinds of sand filters were also selected with particle size in the range of 1.0-1.18, >1.18-1.4, and >1.4-1.7 mm. The Yellow River sediment in the people's Victory Canal was collected as impurity particles in the raw water. The distribution of particle size in the Yellow River sediment was measured using a laser diffraction particle size analyzer (Mastersizer 3000, Dandong Baite Instrument Co., Ltd). It was found that the calculated mean values of skewness and kurtosis were 0.12 and -0.01, respectively, for the samples from the Yellow River sediment, indicating an outstanding normal distribution. Additionally, the samples were also collected from the Yellow River sediment in Lankao County, thereby verifying the distribution of particle size. It was found that the skewness and kurtosis values of the sediment sample in Lankao County were -0.11 and -0.23, respectively, where the frequency distribution of particle size also conformed to the normal distribution. An industrial CT scanner (C16M3201, Luoyang Tengda Testing Service Co., Ltd) was used to map the filter layer. The image processing and pixel coverage were utilized to calculate the porosity of cross section, the box-counting fractal dimension, and the ratio of the minimum to the maximum aperture (aperture ratio) in the three kinds of sand filter layers. The results showed that the porosities were 0.421, 0.431, and 0.439, respectively, while the box-counting fractal dimensions were 1.695, 1.709 and 1.726, respectively, and the aperture ratio was 1/17, 1/18, and 1/21, respectively, for the three types of layers. Then, the applicability of fractal theory was also evaluated for the quartz sand filters. Subsequently, a fractal model of filtration probability was established for the sand filters. The ranges of pore diameter in the three kinds of sand filters were 59.5-1 002, 66.9-1 220, and 72.9-1 503m, respectively. In the sediment of the Yellow River from the people's Victory Canal, the probabilities of impurity particles above 100 um passing through the sand filter were 0.67%, 0.81%, and 0.93%, respectively. In the Yellow River Sediment from Lankao County, the probabilities of impurity particles above 100m passing through the sand filter were 0.62%, 0.80%, and 0.91%, respectively. It inferred that the presence of surface filtration was proved theoretically. A systematic investigation was also made on the influence of surface filtration on Backwash frequency. Consequently, an optimal filter layer was achieved to reduce the surface filtration, particularly with the particle size in the range of >1.4-1.7 mm suitable for sand filters. The finding can provide strong support to explore the internal structure of sand filters and the selection of filter material.
sediments; particle size; image processing; quartz sand filter; box-counting fractal dimension; surface filtration; filtration performance; image processing
李景海,翟国亮,刘清霞,等. 基于分形维数特征的砂滤层适宜粒径范围[J]. 农业工程学报,2021,37(20):162-168.doi:10.11975/j.issn.1002-6819.2021.20.018 http://www.tcsae.org
Li Jinghai, Zhai Guoliang, Liu Qingxia, et al. Suitable particle size range of sand filter layers based on fractal dimension characteristics[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(20): 162-168. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2021.20.018 http://www.tcsae.org
2021-07-09
2021-10-12
中国农业科学院农田灌溉研究所实验室开放基金项目(FIRI2021020101);安阳工学院博士科研启动基金(BSJ20190015);安阳科技计划(2020-199)
李景海,博士,正高级工程师,研究方向为微灌过滤器及水资源配置。Email:649923670@qq.com
刘清霞,讲师,研究方向为建筑材料与水处理。Email:13837246449@163.com
10.11975/j.issn.1002-6819.2021.20.018
S275.6
A
1002-6819(2021)-20-0162-07
