针对财产隐匿人特征分析的基于犹豫模糊语言K-均值聚类算法

王婷琪 张振宇 林 杰

（同济大学 经济与管理学院，上海 200092）

执行难问题严重影响着社会的和谐稳定、法律的公平公正、司法的权威性，被社会广泛关注，最高人民法院采取了一系列措施并取得一定的效果。黄松有对执行难的涵义进行阐述，分析了其主要表现形式以及形成原因，并提出一系列的解决措施。魏建文等认为法律权威性的缺失是司法执行难的本质原因，因此增强社会和公众的法律信仰才是解决问题的根本。潘溪指出，引入第三方评估来分析执行难问题的原因并提出科学的解决方案，对解决执行难问题有一定的帮助。张榕认为执行难主要是因为信用制度的缺失，完善信用惩戒制度、引入法律服务中介机构才能化解执行难问题。

现有的研究主要强调执行难的原因及解决问题的措施等，对被执行人的特征分析较少，尤其是自然人，本文研究主要针对案件执行中有财产隐匿人为自然人的情况进行讨论。财产隐匿人作为执行难问题的主体，根据财产隐匿人的特征对财产隐匿人进行聚类，对于寻找财产隐匿人的主要特征以及执行难问题的解决具有非常重要的意义。

在实际执行程序中，被执行人特征的描述主要通过法官、执行员等专业人士定性分析，通常采用模糊语言的方式对被执行人的特征进行描述。描述被执行人的特征时，考虑到是由多名法官、执行员等专业人士对某一特征评价，通常很难得出一致的意见并出现多个可能语言术语，为避免评价信息的丢失，Rodriguez等引入犹豫模糊语言术语集的概念，给解决此类问题提供了较好的思路。目前，学者们针对犹豫模糊语言术语集展开了大量的研究，提出距离测度和相似性测度、相关系数理论和集结函数，并提出犹豫模糊语言TOPSIS、TODIM、VIKOR等多属性决策方法。

聚类算法作为一种非监督模式识别方法，主要根据数据的类内相似性大和类外相似性小的原则，将一组待聚类对象聚集分成几类的过程。目前被广泛应用在模糊控制、医疗诊断、信息检索等领域。基本聚类算法主要包括基于分层的聚类、基于划分的聚类和基于密度的聚类方法等。作为一种重要的聚类方法，基于划分的聚类方法需要先输入类别个数，主要代表有K-均值算法等。K-均值算法的基本思想是，通过迭代逐次移动各类别的中心，直到得到最好的聚类结果为止。在算法构造过程中，初始类别和类中心的确定直接影响着K-均值算法的迭代效率，目前并没有通用的方法，只能假设而定。

目前，针对犹豫模糊信息的聚类算法有一定的研究。Zhang和Xu基于图论的理想特性，提出一种犹豫模糊最小生成树聚类算法；Chen和Xu提出一种新的犹豫模糊集关联测度，建立关联系数矩阵不断迭代从而得到等价矩阵，并基于-截矩阵进行分类；Chen和Xu将层次聚类的结果作为K-均值聚类的初始类别和类中心，从而使K-均值迭代效率大大提高；Zhang和Xu将凝聚式层次聚类算法拓展到犹豫模糊信息中，并将其拓展到区间犹豫模糊集上，通过实验验证算法的有效性。虽然犹豫模糊信息聚类算法的研究在国内外有一定发展，但对犹豫模糊语言信息聚类算法的研究很少。

基于此，本文将提出一种犹豫模糊语言层次K-均值聚类算法。首先对犹豫模糊语言集的表达方式、距离测度函数以及集成函数进行阐述；其次将犹豫模糊语言集拓展到K-均值聚类算法中，利用层次聚类的结果作为K-均值聚类的初始类别和类中心，提出一种犹豫模糊语言层次K-均值聚类算法；最后通过对有财产隐匿行为人的聚类实例验证了算法可行性。

1 犹豫模糊语言集基础知识

定义1设S＝｛s0，s1，K，sg｝为语言术语集，犹豫模糊语言集HS是S中连续的语言术语项所构成的有序子集。

定义2设xi∈X，且i＝1，2，K，N。S＝｛s0，s1，K，sg｝是语言术语集，则X上的一个犹豫模糊语言术语集的数学形式为

其中，hs（xi）：X→S是定义在集合X上的函数，对任意的元素xi∈X，都有唯一hs（xi）的与其对应。hs（xi）＝｛sδl（xi）｜sδl（xi）∈S，l＝1，2，K，L（xi）｝，δl∈｛0，1，K，g｝为语言术语sδl（xi）的下标，L（xi）表示hs（xi）的语言术语个数。为了方便，称hs（xi）为犹豫模糊语言数，这样犹豫模糊语言术语集HS就是所有犹豫模糊语言数的集合。hs（xi），sδl（xi）和L（xi）可简写为hiS，siδl，Li。

定义3设HSM（xi）＝｛sδjM（xi）｜sδjM（xi）∈S｝和HSN（xi）＝｛sδjN（xi）｜sδjN（xi）∈S｝是定义在属性集合X＝（x1，x2，L，xn）上的两个犹豫模糊语言集，其中xi表示第i个特征属性。设ω＝（ω1，ω2，L，ωn）T为xi的权重向量，且满足的距离测度满足下面的性质：

（1）0≤d（HSM，HSN）≤1；

（2）d（HSM，HSN）＝0，当且仅当HSM＝HSN；

（3）d（HSM，HSN）＝d（HSN，HSM）。

根据海明距离和欧氏距离，犹豫模糊语言加权海明距离和欧式距离可定义为

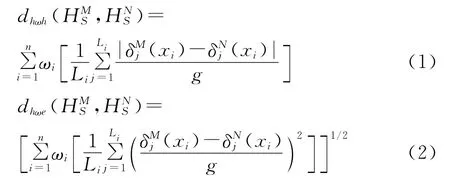
特别地，当ω＝（1／n，1／n，L，1／n）T，则公式（1）和（2）退化为犹豫模糊标准海明距离和欧式距离

其中δMj（xi）和δNj（xi）分别为犹豫模糊语言数HMS（xi）和HNS（xi）中第j大的元素的下标，LMi和LNi分别为犹豫模糊语言数HMS（xi）和HNS（xi）中所含的元素个数，Li＝max（LMi，LNi）。当元素个数不同时，可以采用在元素较少的集合中添加元素的方法，态度悲观者可在集合中添加最小元素，态度乐观者添加最大的元素。

定义4对任意三个犹豫模糊语言数H，H1和H2，λ∈［0，1］运算规则如下所示：

（1）HC＝USα∈H｛Sg－α｝；

（2）H1UH2＝USα∈H1，Sβ∈H2｛Sα∨β｝；

（3）H1IH2＝USα∈H1，Sβ∈H2｛Sα∧β｝；

（4）Hλ＝USα∈H｛（Sα）λ｝＝USα∈H｛Sαλ）；

（5）λH＝USα∈H｛λSα｝＝USα∈H｛Sλα）；

（6）H1⊕H2＝USα∈H1，Sβ∈H2｛Sα⊕Sβ｝＝USα∈H1，Sβ∈H2｛Sα＋β｝；

（7）H1⊗H2＝USα∈H1，Sβ∈H2｛Sα⊗Sβ｝＝USα∈H1，Sβ∈H2｛Sαβ｝。

性质对任意三个犹豫模糊语言数H，H1和H2，都有以下性质：

（1）H1⊕H2＝H2⊕H1；

（2）H1⊗H2＝H2⊗H1；

（3）λ（H1⊕H2）＝λH1⊕λH2，λ＞0；

（4）（H1⊗H2）λ＝Hλ1⊗Hλ2，λ＞0。

定义5设Hi（i＝1，2，L，n）为一组犹豫模糊语言集，则它们的加权平均函数可由下式给出：

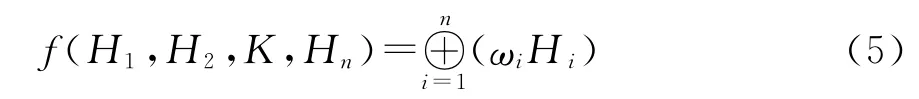
基于犹豫模糊语言集的运算法则，公式可以进一步表示为

特别地，当ω＝（1／n，1／n，L，1／n）T，则公式（5）和（6）退化为

2 基于层次分析的犹豫模糊语言K-均值聚类算法

K-均值算法作为最常见的基于划分的聚类算法之一，首先需给定聚类的类别数，并给定初始类别的划分，计算初始类别的类中心。在传统的K-均值算法中，通常采用随机选择的方式确定初始类别，并通过不断迭代寻找最优的聚类类别。显而易见，随机选择初始类别的方式将增加最终分类方案的迭代次数。针对这一问题，国内外学者对K-均值算法的初始类别确定方法做了大量研究。研究表明，层次结构在选取初始化类别过程中具有较好的效果，尤其是将层次凝聚聚类的结果作为K-均值聚类算法的初始类别，迭代效率远远大于随机选择。因此，本文将这一思想结合犹豫模糊语言环境，提出犹豫模糊语言层次K-均值聚类算法，主要步骤包括以下两部分：

第一部分 层次凝聚聚类

设X＝（x1，x2，L，xn）为属性集合，ω＝（ω1，ω2，L，ωn）T为xi的权重向量，且满足Aj（j＝1，2，K，n）是一组由m个犹豫模糊语言数构成的集合，函数定义为

层次凝聚聚类的思路是，首先将n个犹豫模糊语言集各为一类，其次计算各类之间的距离测度，参照犹豫模糊语言加权海明距离（公式（1））或犹豫模糊语言加权欧几里距离（公式（2）），并将距离最短的两类合并为一类，根据公式（8）计算新的类中心，通过不断的迭代直至将所有目标聚成一类为止。

第二部分 K-均值聚类

步骤1给定聚类的类别数。

步骤2根据类别数将第一部分层次聚类的结果作为初始类，并根据公式（8）计算初始类中心。

步骤3根据公式（1）或（2）计算犹豫模糊语言集与各类中心之间的距离，将前者并入与其距离最近的一类。

步骤4根据步骤3的聚类结果更新类中心，若类中心稳定，迭代停止；若类中心不稳定，重复步骤2和步骤3，直到类中心稳定为止。

3 算例分析

本文以财产隐匿人聚类为例，假定对于特征属性的语言标度S＝｛s0，s1，s2，s3，s4，s5，s6｝，分别表示非常差、比较差、差、一般、好、很好、非常好。现有7个被执行人，分别从收入水平（C1）、语言风格（C2）、交易行为（C3）、消费习惯（C4）进行评价，各特征属性的描述如表1所示。假定各特征属性的权重为ω＝（0.12，0.23，0.37，0.28）T，决策矩阵如表2所示。例如，被执行人A1在属性C1下犹豫模糊语言数为｛s5，s6｝，说明专家们的意见主要集中在很好和非常好之间。

表1 被执行人（自然人）特征属性

表2 犹豫模糊语言决策矩阵

第一部分 层次凝聚聚类

步骤1将每个犹豫模糊语言集Aj（j＝1，2，3，4，5）看作一个独立的类：｛A1｝，｛A2｝，｛A3｝，｛A4｝，｛A5｝。

步骤2根据公式（1）计算各类之间的犹豫模糊语言加权海明距离，距离计算过程中按态度悲观添加元素。

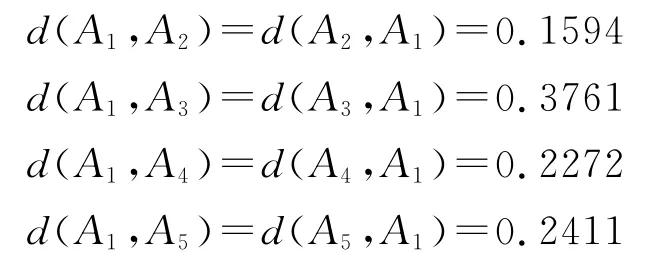
A3和A5距离最近，可将A3和A5两类合并，这样Aj（j＝1，2，3，4，5）被分为下面四类：｛A1｝，｛A2｝，｛A3｝和｛A3，A5｝。

步骤3根据公式（8）计算新的类中心：

计算每一类与其他三类的犹豫模糊语言加权海明距离：

A4和c｛A3，A5｝距离最近，则犹豫模糊语言集Aj（j＝1，2，3，4，5）被分为下面三类：｛A1｝，｛A5｝和｛A3，A4，A5｝。

步骤4根据公式（8）计算每类中心

计算每一类与其他两类的距离：

A1和A2距离最近，则犹豫模糊语言集Aj（j＝1，2，3，4，5）被分为下面两类：｛A1，A2｝和｛A3，A4，A5｝。

最后将两类合并为一类。

第二部分 K-均值聚类

为了执行K-均值聚类，这里选择层次聚类的结果作为初始类别。因为K＝1和K＝5时，结果是唯一的，所以用K＝2，3，4展示我们的算法：

（1）K＝4：用层次聚类的结果｛A1｝，｛A2｝，｛A4｝和｛A3，A5｝作为初始类，计算类中心及每类和中心之间的距离：

基于上述计算的距离可以得到分类｛A1｝，｛A2｝，｛A4｝和｛A3，A5｝。因为每类的中心不变，所以迭代停止。

（2）K＝3：将｛A1｝，｛A2｝和｛A3，A4，A5｝作为初始类，对应结果是：

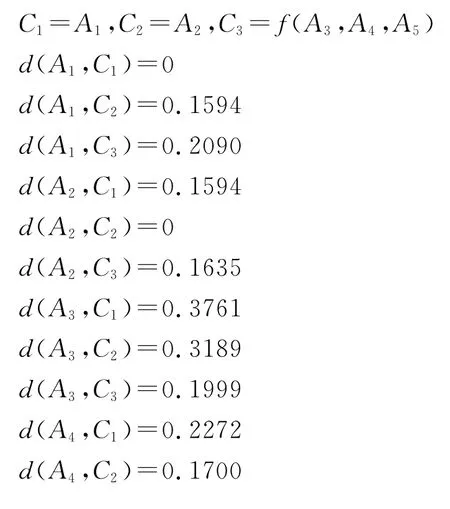
基于上述计算的距离可得到分类｛A1｝，｛A2｝，｛A4｝和｛A3，A5｝，且每类的中心不变，迭代停止。

（3）K＝2：将｛A1，A2｝和｛A3，A4，A5｝作为初始类，对应结果是：

显然，每类的中心不再改变，迭代计算停止，因此分类结果为｛A1，A2｝和｛A2，A4，A5｝。

在此例中，利用层次聚类的结果作为K-均值聚类的初始类别，相对随机选择初始类别来说，可以提高聚类效率、减少迭代次数，快速达到理想聚类结果。

4 结论

实际生活中，对于事物特征属性的评价通常采用模糊语言。犹豫模糊语言较好地贴合评价信息的不确定性和决策者的犹豫模糊性。本文基于犹豫模糊语言的信息表达优势和层次K-均值聚类算法的思想，提出一种犹豫模糊语言层次K-均值聚类算法。首先，构造犹豫模糊语言决策矩阵进行层次凝聚聚类，将每一个犹豫模糊语言集各成一类，计算各类之间的距离测度，将距离最小的两类合并为一类并更新类中心，直至所有目标聚为一类。然后将层次凝聚聚类结果作为K-均值聚类初始类别和类中心，将每个犹豫模糊语言集归入距离最小的一类，直至类中心稳定停止迭代。最后，以有财产隐匿行为人的案件为例进行分析，结果表明，将层次聚类的结果作为K-均值聚类的初始类别，相对随机选择初始类别来说，可以提高聚类效率、减少迭代次数，快速达到理想聚类结果，该聚类算法具有一定的可行性和有效性。