带趋势项ESTAR模型单位根检验的渐进分布

胡俊娟,Murtala Adam Muhammad

(浙江科技学院 理学院,杭州 310023)

近年来,由于STAR(smooth transition autoregression,平滑转换自回归)模型在对时间序列动态中机制转换非线性特征的描述上,具有一般性和灵活性的特点,被广泛应用于汇率[1]、通货膨胀率[2-3]、失业率[4]、股市[5]等金融与经济领域。在日常生活中,宏观时间序列数据通常具有明显的时间趋势特征,在建模前需对时间序列平稳性进行分析,因此对带线性趋势的时间序列进行单位根检验(检验平稳性)具有广泛的实际意义,进而带趋势项STAR模型的单位根检验受到了国内外研究者的广泛关注[6-7]。

对带确定性趋势(或者截距)的线性AR(autoregression,自回归)模型的2种表达形式而言,通过对模型化简可知二者具有相同的波动部分,因此对这2种带确定性趋势的AR模型进行单位根检验会得到一致的结论,然而对带确定性趋势项的STAR过程而言,2种形式却包含了不同的波动部分[6]。如果对这2种形式带趋势项的STAR模型的单位根检验不加以区分,会导致检验结果的不可靠,如Zhang[8]和Kaufmann等[9]针对不同形式带趋势项STAR模型进行了线性检验,所得结论不同。目前关于带趋势ESTAR(exponential smooth transition autoregression,指数平滑转换自回归)模型的单位根检验研究较侧重于去趋势的各种方法[7,10,11],鲜有文献对模型的2种不同形式加以区别研究。因此,我们对ESTAR模型2种形式的单位根检验进行研究,基于模型在不同形式下相应的辅助方程,考察KSS(Kapetanios-Shin-Snell)检验统计量的极限分布,从而对2种形式单位根检验从根本上加以区分,并且还为拓宽对带确定性趋势项STAR模型的单位根检验的研究打下一定的理论基础。

1 KSS检验

考虑以下一阶带确定性趋势项ESTAR模型:

(1)

或

(2)

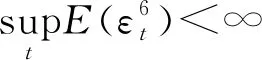
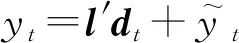
(3)

式(3)中:et为误差项。进一步,Kapetanios等[12]363提出了检验H0:δ=0的t检验(又称KSS检验),检验统计量tKSS的极限分布为

(4)

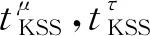
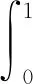
2 主要结论

KSS检验统计量的极限分布是基于OLS去趋势方法进行的,即考察的是基于式(2)模型的单位根检验。对式(1)通过泰勒展开可以得到以下辅助方程:

(5)

定理1假设Δyt=εt,则

“⟹”表示弱收敛。在备择假设下,即基于式(5)(b=0)情况下带均值ESTAR模型的检验统计量tμ具有一致性,且以速率T(样本量)收敛。

证明:根据辅助方程式(5)(b=0),在原假设H0下OLS估计量

根据定理1的假设,则在辅助方程式(5)中ut=εt。根据随机积分的弱收敛定理和εt的半鞅性质[14],则有

因此我们可以得到

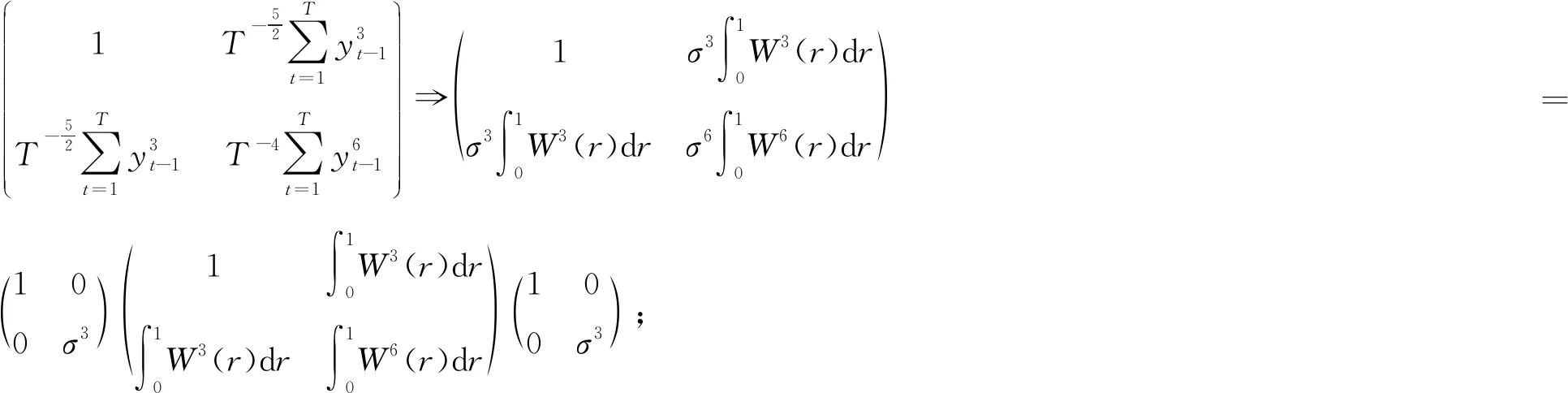
进一步有

则

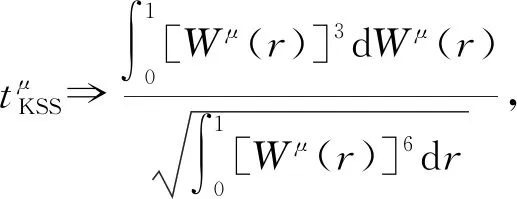
通过对上述极限分布的对比发现,对于具有均值过程的时序,基于式(1)和式(2)的模型检验统计量极限分布不一致,因此临界值不一样,对这2种形式的模型不加以区分,直接用去趋势KSS检验临界值对式(1)进行单位根检验,所得检验结果必定不可靠。

定理2假设Δyt=a+εt且y0=0,则

(6)

式(6)中:A11、A12、A21、A22和B1、B2分别为矩阵A(W(r))、B(W(r))的分块矩阵,具体形式参见以下证明。

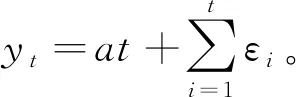
不妨记

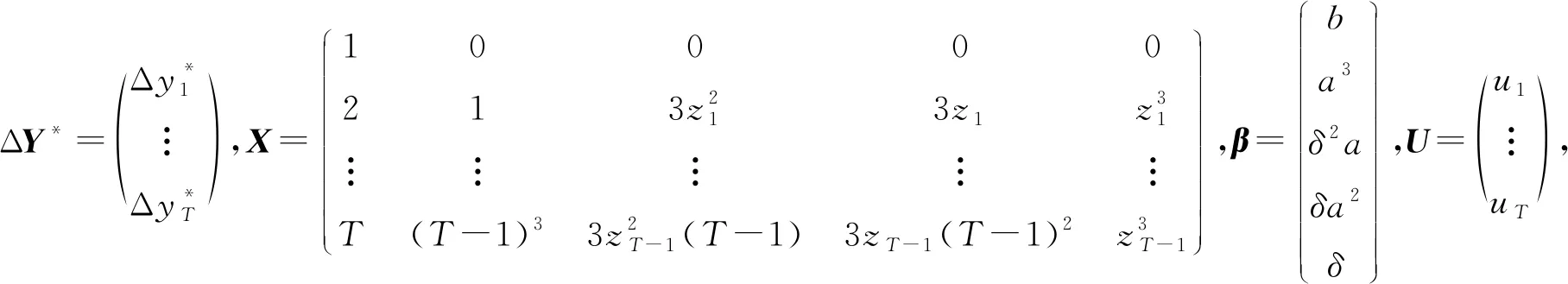
根据连续映射定理,我们可以得到[γ-1(X′X)γ-1]⟹H(W(r),σ),且[γ-1(X′ε)]⟹Q(W(r),σ),其中

因为在原假设下H0:δ=0可以写成H0:Rβ=0,其中R=(0 0 0 0 1),则通过计算可得

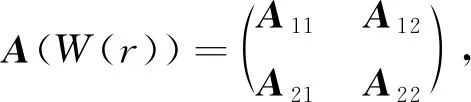
因此,则有

得证。

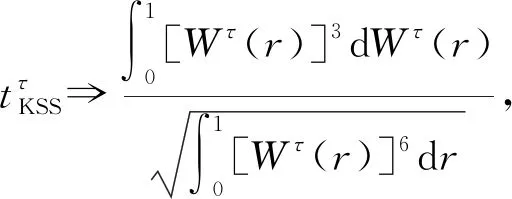
3 结 语

定理1和定理2说明了不同形式带趋势项的ESTAR模型t检验统计量的极限分布并不相同,因此在分析带趋势项过程时,单纯地使用先去趋势然后用常用的临界值表检验法并不十分科学。考虑到带趋势项的非线性ESTAR模型的2种形式导致的波动不一致,本研究从理论角度给出了证明,这一结果为带确定性趋势项ESTAR模型单位根检验的研究提供了理论参考,故建议在采用带趋势项ESTAR模型建模分析数据时,应对采用式(1)还是式(2)加以区分。本研究侧重考虑的是带趋势项ESTAR模型的2种不同形式的极限理论,考察的是常用的线性趋势部分,接下来我们将会把研究进一步扩展到傅里叶趋势[16]情景中去,以进一步拓宽带趋势项ESTAR模型单位根检验的研究思路。