基于步降应力加速试验的联轴器寿命估计
2021-12-28王录祁涛
王录,祁涛
(200093 上海市 上海理工大学 机械工程学院)
0 引言
评估产品可靠性的加速实验方法基本可以分为加速寿命试验(ALT)与加速退化试验(ADT)。根据试验过程中施加应力方式的不同,加速寿命试验主要分为恒定应力试验、步进应力试验和序进应力试验3 种基本的加速寿命类型[1-3]。除此之外,文献[4]提出了步降应力试验,文献[5]提出了循环序进应力试验,文献[6]提出了随机应力试验,文献[7]提出了双应力加速寿命试验等加速寿命试验方法。其中,恒定应力试验的理论方法最成熟,而且评估结果的精度也相对较高,其缺点是在试验过程中需要花费较长时间和较多样本量。与恒定应力试验相比,序进应力试验具有样本消耗少、花费时间短等优点,但是其缺是对设备的要求较高,施加的负载不好控制而且目前评估方法也不成熟,目前的技术难以满足其要求,所以还只是停留在理论层面的研究[8]。
长期以来,高可靠长寿命的量化估计一直是可靠性工程领域的一个技术难题。联轴器作为动力传输结构,在工作中会由于疲劳造成联轴器的性能退化,进而损坏机械传动系统,为了防患于未然,研究联轴器的寿命可靠性对机器的安全运转、维护维修具有重要意义。步降应力试验相比步进应力试验和恒定应力,可以大大减少试验样本,减少试验花费的时间,并且目前研究的理论方法也较为成熟。综合以上,本文采用步降应力加速试验方法,对绕线联轴器的使用寿命进行评估,并与恒定应力下的试验结果进行比较,验证步降应力加速寿命试验方法的有效性。
1 加速退化试验的方案
1.1 基本假设
当产品的寿命分布为Weibull 分布时,对试验数据进行统计分析和模型推导做出了以下4 个基本假定[9]:
(1)正常存储和加速应力条件下,产品所受步降应力,S1>S2>S3>…>Sk产品的寿命服从两参数weibull 分布(mi,ηi),其分布函数为
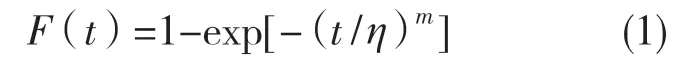
其密度函数为

可靠度函数为

其失效率函数为
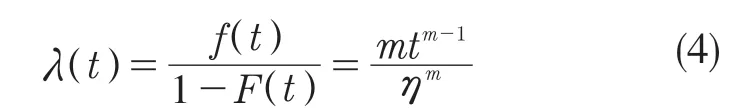
式中:t——故障时间;m——形状参数;η——特征寿命。
(2)产品在应力S1,S2,S3,……Sk下的失效机理与正常应力下的失效机理相同,也就是在各应力下的产品寿命分布的形状参数保持不变:

(3)产品的特征寿命和所见应力的关系为

加速模型采用逆幂律模型

式中:ξ——某寿命特征;A,n——常数;S——应力水平。因为服从Weibull 分布,对式(6)两边取对数,可得线性化的逆幂律模型

(4)Nelson 累积失效模型的假设
Nelson 累积损伤模型表述了样本的残余寿命只依赖于已经累积的失效和当前的应力,与累积的方式无关。根据Nelson 模型可以得到在不同的应力水平下寿命时间可以相互折算。
综上,本文步降应力试验的四大假设为:Weibull 分布假设、失效机理不变假设、加速模型假设和Nelson 累积失效模型假设。
1.2 试验统计概率模型
步降应力试验累积失效的基本过程为:在k阶步降应力加速试验中,其步降应力大小分别为Sk,Sk-1,…,S1,对应的加载时间ti+1-ti,ti-ti-1,…,t2-t1,且对应的失效分布函数分别为Fi(t),Fi-1(t),…,F1(t),产品在整个步降退化试验中的总体累积失效概率为F0(t)[10]:
(1)产品在第k 阶的总体累积失效概率函数为

(2)产品在第k-1 阶的总体累积失效概率函数为

(3)一般而言,产品的总体累积失效概率函数为

由上述可知,除了最高应力水平Sk以外,步降应力加速试验在其他加速应力水平(Sk-1,Sk-2,…,S1)得到的失效数据均不是完整的失效样本,累积试验时间须通过应力水平之间的数据转换来估计。如图1 所示,将所有应力水平S1之前的试验时间转换至S1,以这样的方式得到的试验时间是该试件的完整失效时间。图1 中应力从S3步降到S1,假设绕线联轴器在应力S1下经t1时间后失效,那么联轴器失效的累计时间不仅仅是t1,t2,t3的累积,还要包括应力S2和S3作用时间在S1上的折算,如图1 所示.总试验时间为
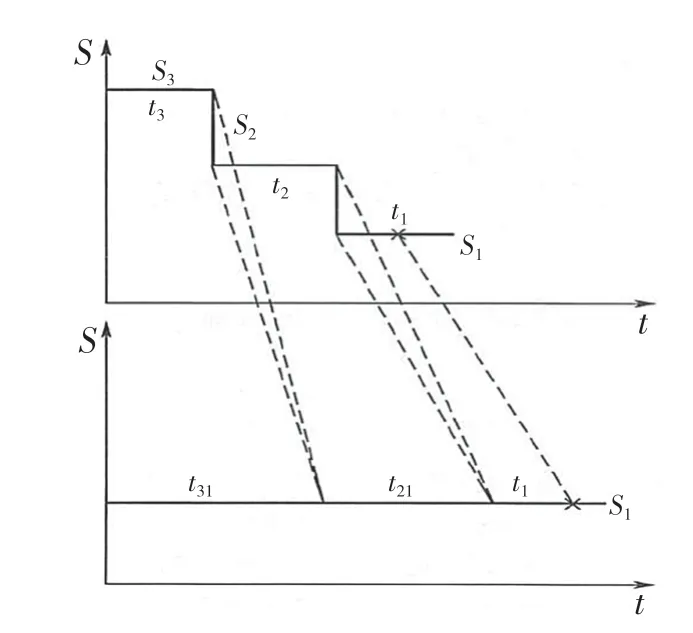
图1 步降应力试验累积时间折算Fig.1 Step-down stress test cumulative time conversion

1.3 加速因子
绕线联轴寿命分布器满足Weibull 分布时,其加速因子为kij=ηj/ηi,不同应力水平失效数据的折算公式为

1.4 基于加速模型的数据折算
为了估计模型参数,首先需要进行应力数据折算,数据折算时依据Nelson 模型,试件在应力水平Si下工作ti时间内累积失效概率Fi(ti),相当于在应力水平Sj下工作tj时间内累积失效概率Fj(tj),则

根据失效机理不变假设,可得mi=mj,因而有

结合式(6)可得

式(15)表达了不同应力下等效时间的换算关系。假设步降应力试验中采用k 个应力,其中S1>S2>S3>…>Sk,样本数量为n 个。在应力Si下有ri个数据失效(失效时间分别为)。本文数据折算过程中,所有数据都换算到最大应力处,也就是将所有的应力Si下的数据都折算成S1下的数据。折算后的数据为
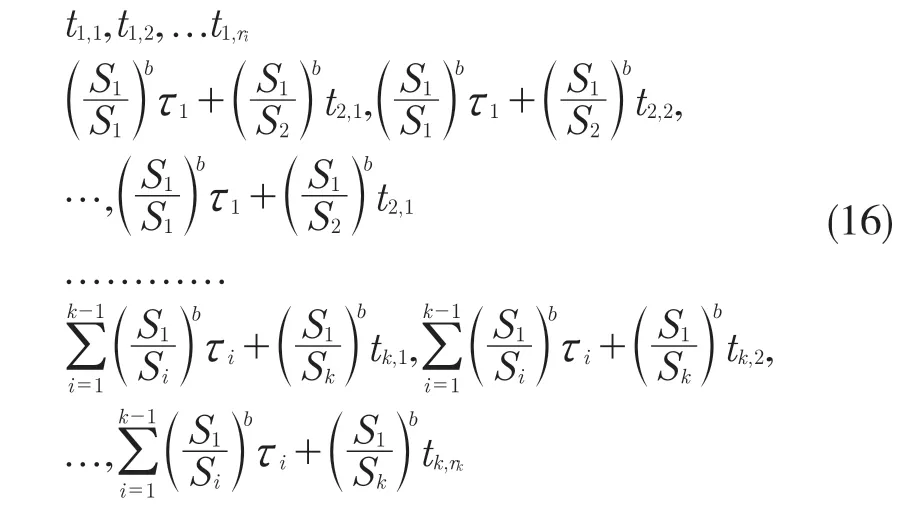
式中:τi=ti,ri。将折算后的数据记为ti(b)。

式中:r=r1+r2+…+rk。
1.5 Weibull 分布函数的参数估计
Weibull 分布函数的参数估计目前常用的方法有极大似然估计法[11-12]和逆矩估计法[13]。本文采用了逆距估计法。

式中:ti(b)——折算后的数据。
通过式(18),建立逆距估计公式如下:
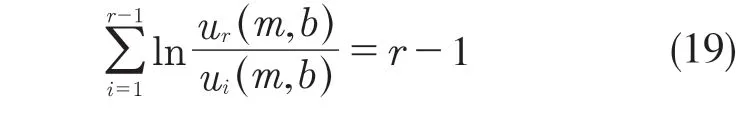
使用m 的最佳无偏估计,可得

其中,C(n,r,i),nkn,r可在“可靠性试验用表”中查找,可获得b 的参数估计。在应力S1下的特征寿命即为
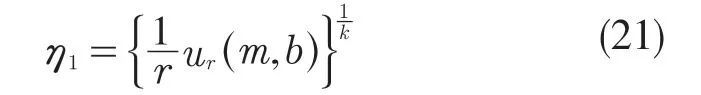
2 试验研究
2.1 加速应力水平的选择
加速应力作为加速退化试验中最关键的参数,在确定其具体参数时有严格的标准,必须能够满足研究的要求,具体包括:选择的加速应力必须在不改变产品失效机理的前提下工作,以此大大缩短试验周期;选择的加速应力必须具有实用性和易用性,同时能最大限度地加快试验进程。
结合绕线联轴器实际工况和失效机理,本文的加速应力选择为扭矩,以扭转刚度作为绕线联轴器可靠性的评判依据。扭矩选择考虑到数据统计和分析的需要应遵循以下基本原则[14-15]:(1)考虑到数理统计和分析的要求,应力不能少于3 个;(2)施加的最大扭矩不得大于该样品结构材料、制造工艺等所能承受的极限,避免带来新的失效机理;(3)一个应力水平应接近或等于该样品标准中所规定的额定值,且最大应力和最小应力之间有较大的间隔。
绕线联轴器正常工作扭矩值为0.75 N·m,当载荷值大于3 N·m 时,绕线联轴器的实际扭转刚度将超过许用扭转刚度要求,影响绕线联轴器的实际失效机理。最低应力水平应高于正常工况,最高应力水平应该在允许范围内尽可能大,所以选取 1.5 N·m 和 3 N·m 作为载荷的最低和最高水平。载荷属于机械应力,根据逆幂律模型的原理,应力往往以对数形式存在,所以加载载荷采用对数等间隔形式,加载应力分别为1.5,2.2,3 N·m;
2.2 退化量的选择
对绕线联轴器而言,扭转刚度是反映其传动性能的重要指标。联轴器工作时,要求输入轴与输出轴转角尽可能一致,结合绕线联轴器失效机理分析,及绕线联轴器本身实际工作情况,确定以扭转刚度作为绕线联轴器可靠性的评判依据。根据实际工况得知,当联轴器扭矩滞后量参数达到40°时工件失效,所以本文将失效阈值设定为当绕线联轴器的扭矩滞后量参数降低到 40°。
2.3 试验设计方案
(1)本文每个应力下对5 个绕线联轴器进行步降应力试验。
(2)将样品在扭矩为3 N·m 下进行试验,到达时间后对样品进行检测,根据上述阈值去掉失效样品,其余继续试验。
(3)将应力降低到2.2 N·m 继续试验重复步骤(2)。
(4)将应力降低到1.5 N·m 重复步骤(2)到达规定的截尾点为止,试验结束。
为了减小离心力的影响,将电机的转速设为100 sin(1πt)r/min,试验所需测试系统整体结构如图2 所示。

图2 测试系统整体结构图Fig.2 Overall structure of test system
2.4 截尾方式的选取
截尾方式采用了定数结尾,考虑到数据转换时,统计分析的精度定数截尾试验应保证50%以上的样品失效,因此步降应力加速寿命试验应采用不对称定数截尾设计[16],即

加载载荷为3,2.2,1.5 N·m 时,试验数据采集次数分别为[9,4,4]。
2.5 试验数据处理及初步分析
3.0 ,2.2,1.5 N·m 三个应力,每个应力下5个样本。

表1 各检测时刻绕线联轴器性能退化Tab.1 Performance degradation of winding coupling at each detection time
将3 N·m 和2.2 N·m 下的试验时间依次折算为恒定应力下的试验时间,将转换后的试验时间和性能下降数据组成数据对,采用基于样本伪失效寿命的方法进行分析,利用最小二乘法原理对各样本的退化模型参数进行估计,得到各样本的退化轨迹模型,将失效阈值Df=40 分别代入15 个退化轨迹方程,得到试样的拟失效寿命,如表2 所示。
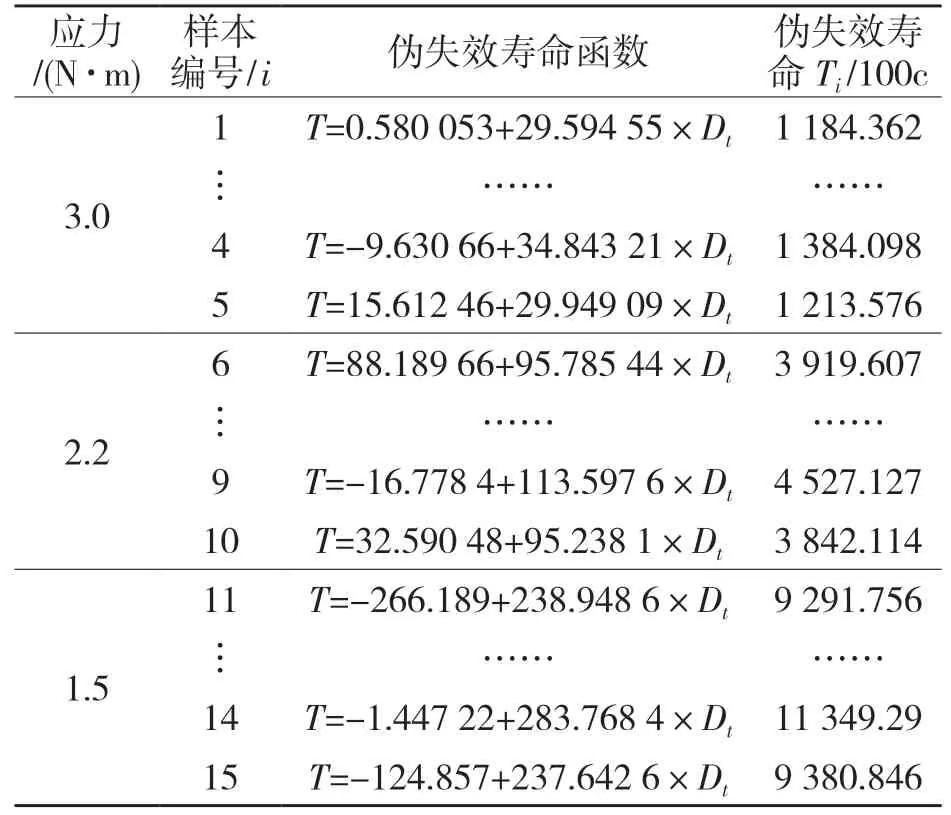
表2 性能退化轨迹方程及伪失效寿命Tab.1 Performance degradation trajectory equation and pseudo failure life
2.6 模型参数估计
在步降应力试验中,共计得到了5 个样本的失效时间数据,采用逆距估计法计算其参数值,本文中r=5<25 。由“可靠性试验用表”[17]得到其线性无偏估计系数,由式(20)可得到在正常使用应力作用下的形状参数

以及其特征寿命
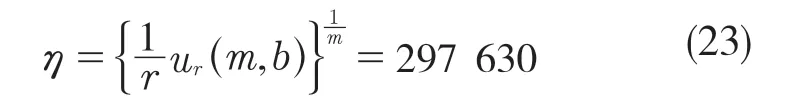
试验对绕线联轴器的使用寿命进行了评估。由式(3)可以得到,在可靠度为0.95 时,寿命值为2.2×107转。正常工况下,绕线联轴器转速为1 000 r/min,可以推算出,在正常工况下,绕线联轴器可以连续工作370 h。
前期,笔者曾采用恒定应力进行试验分析,结果表明,在可靠度为0.95 时,绕线联轴器的寿命值为2.4×107转。也就是可以连续工作400 h。两种试验结果比较可得,采用步降应力和恒应力的评估结果相差不大,但是步降应力试验大大减少了试验周期。
3 结论
基于Weibull 分布和逆幂律模型,采用步降应力的加速退化试验,得到了D25L30 绕线联轴器在加速应力为扭矩下的使用寿命评估方法,利用逆距估计对各样本的退化模型参数进行估计,最终得到了当可靠度为0.95 时的使用寿命。并且与恒应力下的试验结果进行比较,结果显示相差并不大。
