下肢康复外骨骼设计与平地行走轨迹规划

黄玉琳

（200093 上海市 上海理工大学）

0 引言

社会老龄化趋势不断加剧[1]，偏瘫中风等神经疾病以及意外事故造成运动功能障碍的人群数量不断增长，严重影响了他们生活，他们的运动功能康复是目前需要解决的一道难题[2]。下肢助康复骨骼机器人作为一款可穿戴式的智能机械设备，能够帮助老年人以及运动障碍的人进行康复训练，逐渐恢复正常行走[3]，为他们能够独立外出提供了可能性。与国外相比，我国在下肢外骨骼研究方向起步比较晚[4]，研究还处于初级阶段，但是国内也在大力发展。目前国内许多机构高度重视下肢外骨骼的研究，尤其是在康复与助行方面。国内具有代表性的下肢外骨骼机器人有上海傅利叶的Fourier X1[5]，智能傲鲨科技的HEMSGS，迈步科技的BEAR-A1 和杭州程天的UGO 等。

为了对下肢运动障碍患者进行康复训练，本文设计了一款下肢康复外骨骼机器人，利用SolidWorks 软件建立下肢康复外骨骼机器人的三维模型，采用D-H 法建立运动学模型[6]。为达到稳定行走的要求，采用五次多项轨迹规划法，分别对起步、中步和止步状态的髋关节与踝关节进行轨迹规划[7]，在ADAMS 建立虚拟样机环境，利用ADAMS-MATLAB 联合仿真，验证轨迹规划的正确性。

1 机械结构设计

1.1 外骨骼尺寸设计

不同的人下肢尺寸各不相同，为了适应绝大部分人群的穿戴要求，大腿与小腿以及髋关节尺寸需要设计成具有一定长度调节功能的形式[8]，参照GB 10000-1988《中国成年人人体尺寸》[9]，确定各部位的尺寸参数如表1 所示。

表1 人体尺寸参数Tab.1 Body size parameters

1.2 结构设计

人体下肢骨骼主要包括大腿杆骨骼和小腿杆骨骼以及足部骨骼3 个部分[10]。由图1 分析可知：髋关节处有 3 个自由度，即旋内/旋外、伸展/弯曲、外展/内敛；膝关节处有 1 个自由度，即伸展/弯曲；踝关节处有 3 个自由度，即伸展/弯曲、外展/内敛、旋内/旋外。

图1 人体下肢自由度Fig.1 Degrees of freedom of human lower limbs

为满足人体穿戴舒适性和拟人化，下肢外骨骼的自由度应与人体下肢自由度相同。在保证稳定性的情况下，确定外骨骼机器人的总体自由度为四自由度。如图2 所示，分别为髋关节伸展/弯曲与外展/内敛2 个自由度，膝关节伸展/弯曲1 个自由度，踝关节伸展/弯曲1 个自由度。

图2 下肢外骨骼自由度Fig.2 Degrees of freedom of lower extremity exoskeleton

行走时，髋关节与膝关节提供力矩比较大，选择将髋关节与膝关节作为主动驱动，踝关节和髋关节外展/内敛自由度设计为被动驱动。采用超薄电机与谐波减速器作为驱动方案。

2 运动学建模

2.1 D-H 模型建立

下肢外骨骼左右腿是对称的，只需要建立一条腿的模型即可，简化为连杆模型，如图3 所示。建立如图单腿D-H 坐标系。图3 中：l1——大腿长度；l2——小腿长度；L3——踝关节到脚长度；θ1——髋关节角度；θ2——膝关节角度；θ3——踝关节角度。D-H 参数见表2。

图3 连杆模型Fig.3 Connecting rod model

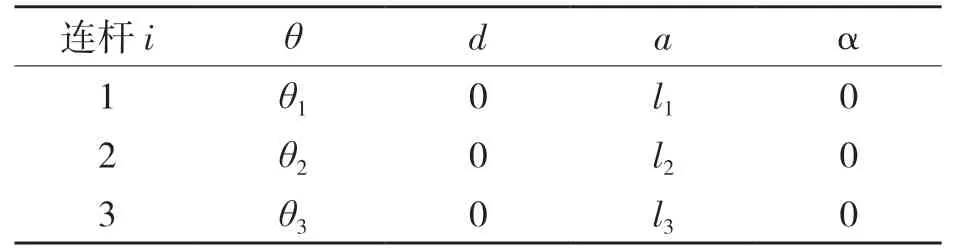
表2 D-H 参数Tab.2 D-H parameters

其中A1，A2，A3为连杆1—连杆3 的变换矩阵，0T3为足端到髋关节的变换矩阵，ci=cosθi，si=sinθi。

2.2 运动学逆解

运动学逆解就是在给定下肢外骨骼机器人踝关节位置与姿态后，即已知大腿与小腿长度的情况下，可求得髋关节与膝关节的转动角度角。在逆运动学求解中，为降低求解难度，利用最简单的几何法求出关节角度逆解。参见图4。

图4 运动学逆解Fig.4 Inverse kinematics solution

以O 点为原点，a 为公共边，根据足端坐标（x，y），有a2=x2+y2。

根据余弦定理可得

3 步态规划

根据人行走特征，将平地行走过程分成3 个阶段，分别是起步、中步和止步。

3.1 起步阶段

下肢外骨骼机器人从双足垂直于地面状态到正常行走状态这一阶段称为起步。在此阶段，其中一条腿作为支撑腿，另一条腿进行迈步，迈步的距离为正常行走迈步的一半。

列出迈步腿踝关节轨迹与髋关节轨迹约束方程，设x 方向为水平方向，y 为竖直方向，髋关节点坐标为（x1，y1），踝关节点坐标为（x3，y3）位移、速度和加速度的约束方程如下：

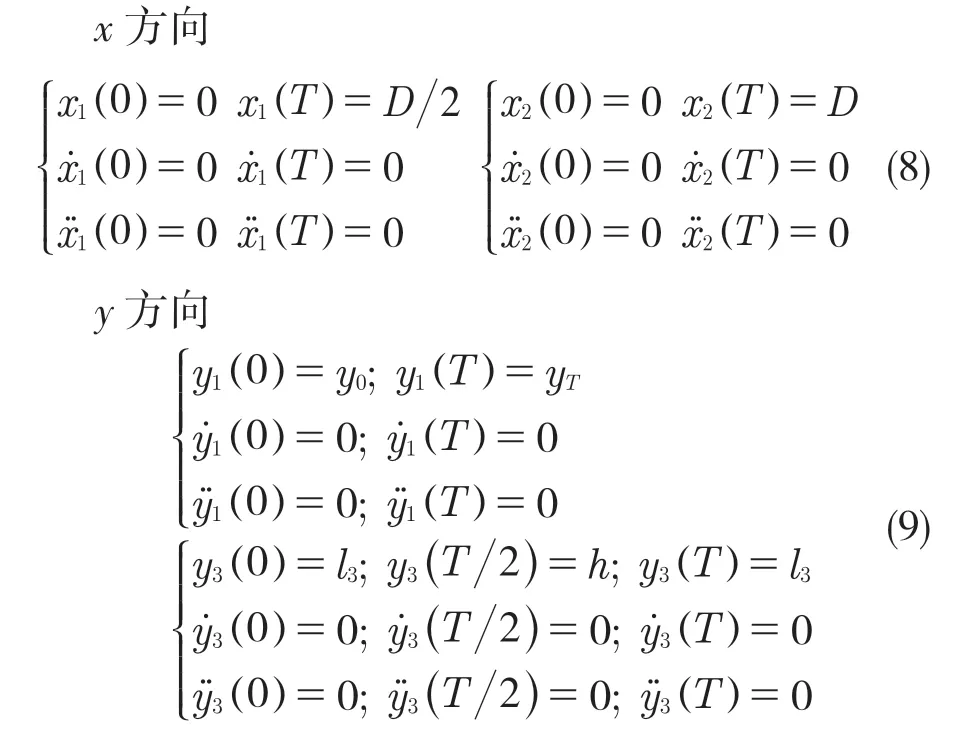
为了保证下肢外骨骼起步与落脚时的稳定性，减少与地面的冲击，故初始与摆动腿落地时，x，y 方向加速度与速度都为0。

最后，采用5 次多项式插值法进行髋关节与踝关节的轨迹规划。x，y 方向的运动轨迹方程可以写为

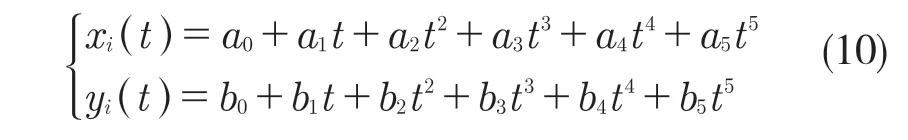
其中i=1，2；a0，…，a5和b0，…，b5为待定系数。将约束公式代入式（10），求解待定系数，得到需要的轨迹。

根据人实际步行要求，设置起步需要总的时间T=1 s，迈步腿步长D=360 mm，踝关节最高点为h=100 mm，踝关节到脚底的距离为l1=40 mm。确定这些参数后，可以得出如图5所示的髋关节与踝关节轨迹图。

图5 起步棍状图Fig.5 Starting stick chart

棍状图5 显示了起步状态各个关节的运动变化。其中，实线、虚线和点画线分别表示髋关节轨迹，摆动腿膝关节轨迹和踝关节轨迹。根据已知的每个时刻踝关节与髋关节的位置，利用运动学逆解可以得到髋关节与膝关节的关节角度变换轨迹，如图6 所示。

图6 起步关节角度变化Fig.6 Change of starting joint angle

3.2 中步阶段

中步状态时，迈步腿从抬起到落地，同样使用时间为T=1 s，迈步的距离为2D。另外一条腿作为支撑腿。同样给定约束条件：

同样得到中步状态关节轨迹棍状图，见图7。根据运动学逆解得到髋关节与膝关节的关节角度变换轨迹，见图8。

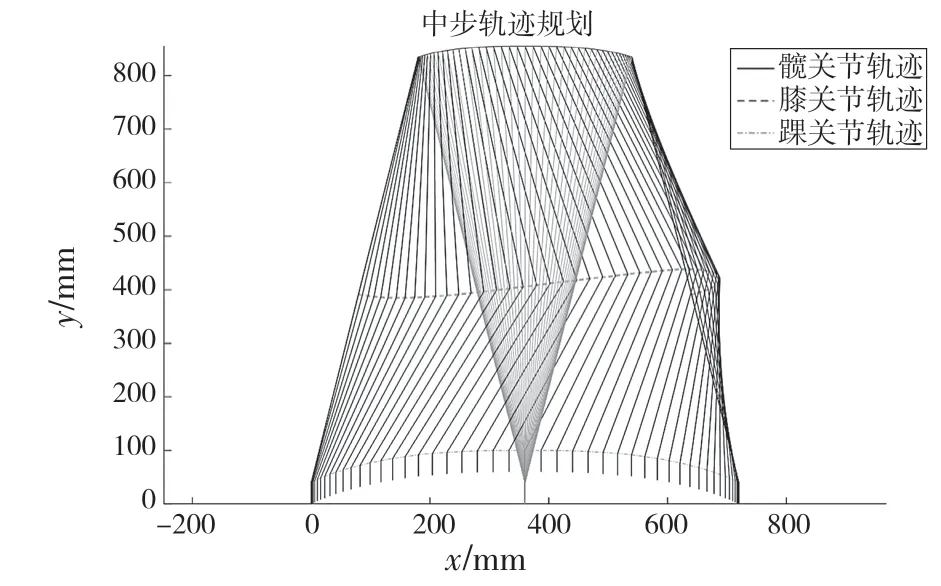
图7 中步棍状图Fig.7 Middle step stick chart

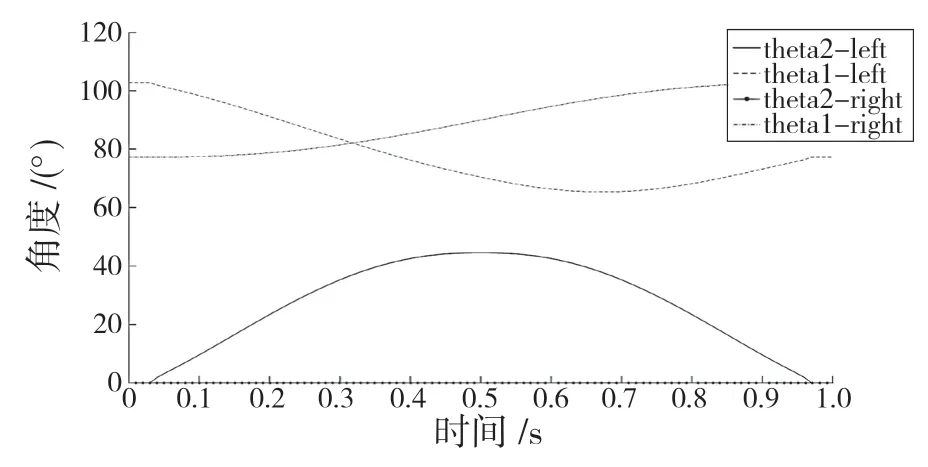
图8 中步关节角度变化Fig.8 Changes of joint angle in middle step

3.3 止步阶段

止步和起步类似，给定约束条件后代入五次多项式，求出待定系数。棍状图如图9 所示。髋关节与膝关节的关节角度变换轨迹，如图10 所示。

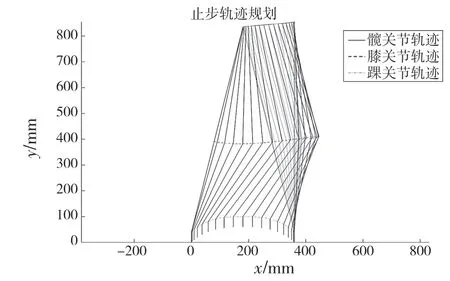
图9 止步棍状图Fig.9 Stick figure of ending gait

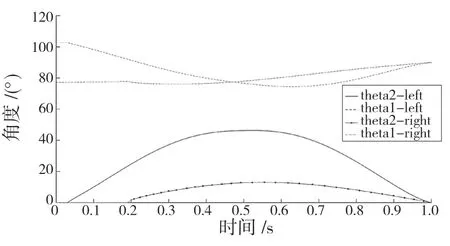
图10 止步角度变化Fig.10 Stop gait angle change

4 联合仿真

4.1 ADAMS 虚拟机建立

将模型从SolidWorks 导出为x_t 格式，导入到ADAMS 中。定义转动副与驱动。下肢外骨骼与环境的关系通过脚与地面实现，在脚与地面设置接触力。参见图11。

图11 ADAMS 虚拟机建立Fig.11 Establishment of ADAMS virtual machine

下肢外骨骼采用电机驱动关节，总共4 个驱动关节，定义为输入变量。

4.2 联合仿真平台搭建

为了验证轨迹规划的正确性，需要将ADAMS 中的模型作为控制对象，从MATLAB 里输出数据。图12 是ADAMS 中导出的机械系统，图13 是整个控制程序。

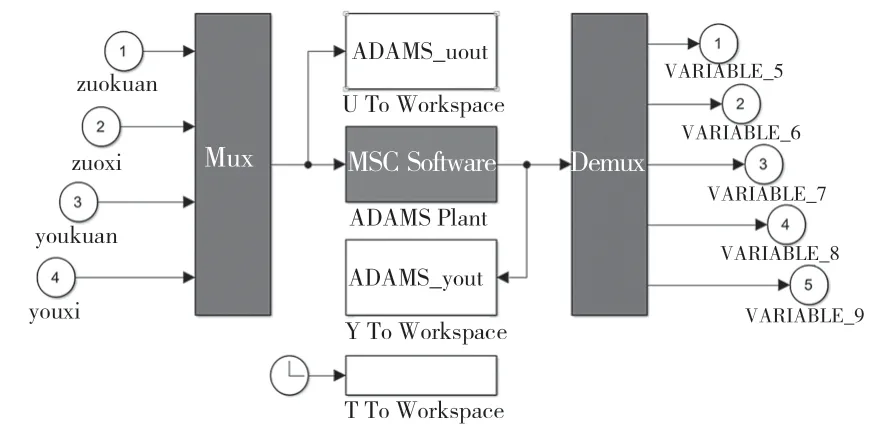
图12 ADAMS 机械系统Fig.12 ADAMS mechanical system

图13 Simulink 控制系统Fig.13 Simulink control system

从仿真结果动画中可以看出，下肢外骨骼机器人能够实现稳定行走。图14、图15 分别是上半身质心在前进与竖直方向的位移。

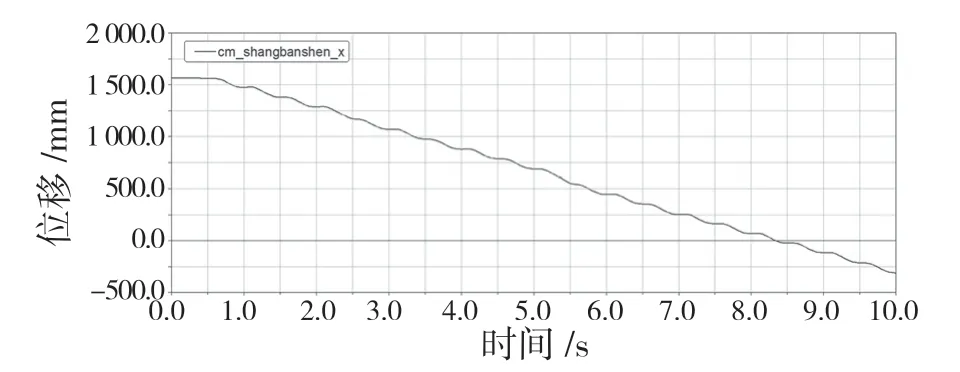
图14 质心行走方向位移Fig.14 Moving direction displacement of centroid

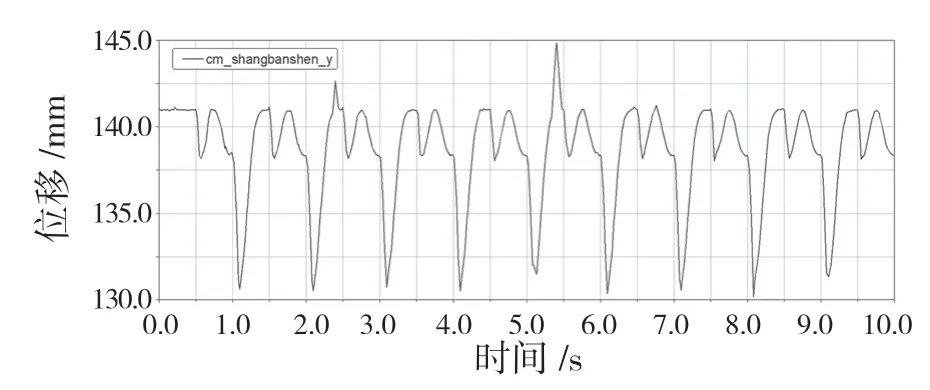
图15 质心垂直位移Fig.15 Vertical displacement of centroid

5 结语

本文设计了一款下肢康复外骨骼机器人，采用SolidWorks 建模，通过五次多项式轨迹规划法对起步、中步和止步进行髋关节和踝关节轨迹规划，并通过ADAMS 和MATLAB 进行了联合仿真，下肢康复外骨骼机器人能够稳定行走，验证了平地行走轨迹规划的正确性。