基于变论域模糊控制的运载火箭姿态控制设计
2021-12-28陈亚军
陈亚军
(200093 上海市 上海理工大学)
0 引言
运载火箭的姿态运动在飞行过程中会受到各种内外不确定性的影响,而模糊控制是一种不依靠控制对象的设计的控制方法,对内外扰动具有较好的鲁棒性。模糊控制在姿态控制的应用基本上与其他控制方法结合在一起。相关研究中,石志华[1]提出一种模糊滑模控制方法,利用模糊控制削弱滑模抖振,该方法对内外干扰表现出较好的鲁棒性;周锐[2]则是把模糊控制和H ∞鲁棒控制结合起来,建立了一种模糊参数化的增益调参飞控系统鲁棒设计方法;于凤仙[3]利用BP 神经网络表达模糊控制系统的知识规则、模糊推理和学习算法,应用于导弹的姿态控制。而目前单一的模糊控制应用于火箭姿态控制仅有文献[4],在文献预置校正网络的基础上,提出了一种基于比例因子和调整因子自调整的自适应模糊控制方法。该方法对参数的适应性强,但是模糊控制器的设计需要根据经验反复调试。
目前模糊控制在运载火箭姿态控制之中应用较少的原因主要有两点:(1)模糊控制精度不高,控制效果粗糙;(2)模糊控制器设计很大一部分依靠设计者的经验,调试麻烦,很难量化设计。
本文提出的简易变论域模糊控制动态性能好,控制精度高,而且控制器的设计只需要调整量化因子、比例因子和伸缩因子即可。
1 运载火箭俯仰通道动力学模型
考虑到箭体的弹性振动和推进剂晃动,箭体质心动力学方程、绕质心动力学方程、弹性振动运动方程以及推进剂晃动运动方程如下:
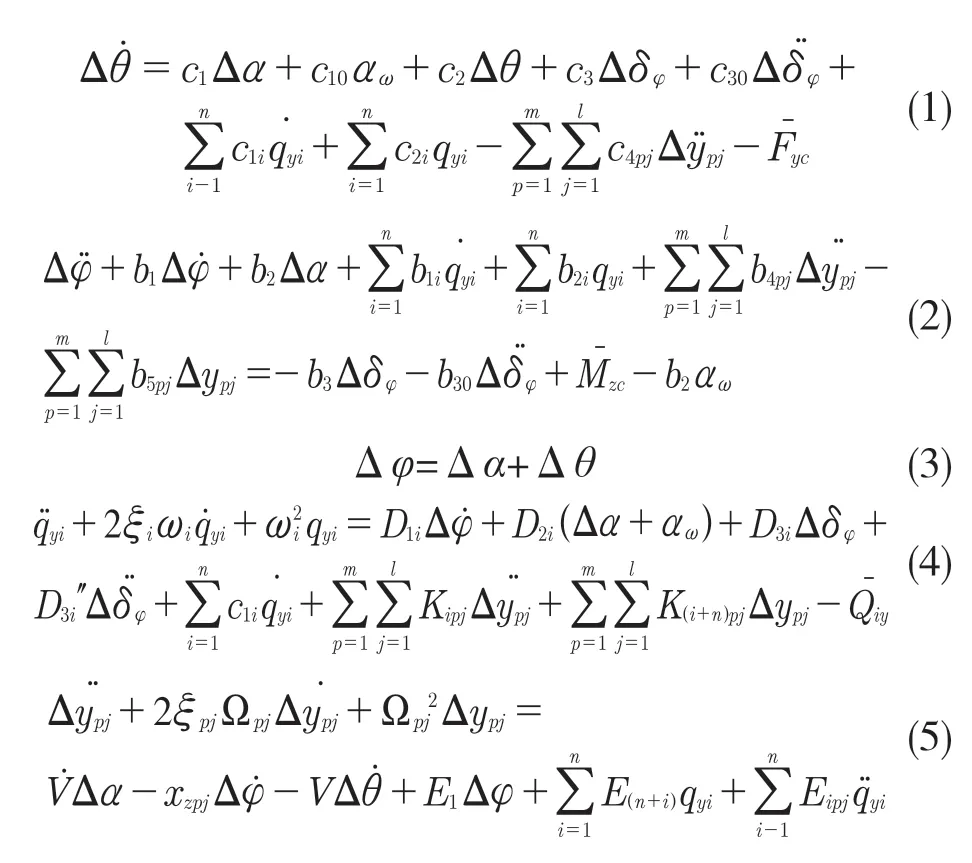
式中:Δθ,Δφ,Δα,αω——弹道倾角、俯仰角、攻角偏差和风扰动引起的附加攻角;Δδφ——俯仰通道的发动机摆角;V,——弹道切向速度和切向加速度;Δypj,ζpj,Ωpj——贮箱等效晃动质量位移、阻尼系数和圆频率;ωi,qi,ζi——第i阶横向振动圆频率、广义坐标和阻尼系数。,——干扰力、干扰力矩系数和广义干扰力矩系数。其他系数参考文献[5]。
测量方程
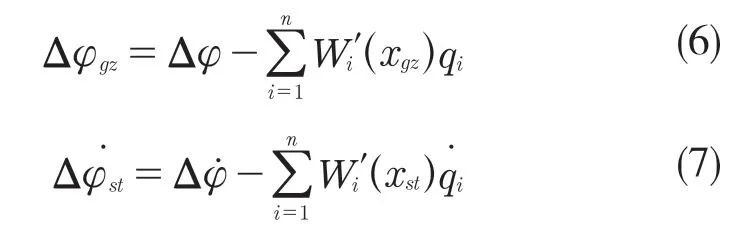
2 变论域模糊控制器设计
传统的模糊控制器隶属度和模糊规则的设计需要专家知识的参与,而且由于控制精度和模糊集数量有关,模糊集数量越多,控制效果越精细,但是模糊规则也会随之大幅增加,一方面影响模糊系统的实时性,另一方面对于规则的设计也造成困难,很难利用经验设计,所设计的规则不具有客观性,不能解释规则设计的原因,可解释性较差,而变论域模糊控制很好地改善了这一点。变论域模糊控制器在模糊规则不变的前提下,论域随着误差变小而收缩,或随着误差增大而增大,使控制器在期望控制点的控制规则大幅增加,从而达到提高控制精度的目的。因此论域是否等距划分,隶属度函数取什么形状,模糊集的多少都对控制器的性能影响不大[6]。基于上述理由,本文选择一种简易变论域模糊控制器。
2.1 变论域模糊控制器结构
如图1 所示,变论域模糊控制器的输入x1为测量俯仰角偏差与指令控制信号的差Δφc,输入x2为测量姿态角速度。

图1 基于变论域模糊控制的姿态控制系统结构图Fig.1 Structure diagram of attitude control system based on variable universe fuzzy control
设Xi=[-E,E](i=1,2,…,n)为输入变量xi(i=1,2,…,n)的论域,Y=[-U,U]为输出变量y 的论域。Φ={Aij}(l≤j≤m)为Xi(i=1,2,…,n)上的模糊划分[7],Θ={Bj}(l≤j ≤m)为Y 上的模糊划分,其中Φ,Θ 为语言变量,那么相对应的模糊规则为

设xij分别为Aij的峰点,yj分别为Bj的峰点(i=1,2,…,m)。则式(8)可以用一个插值函数代替
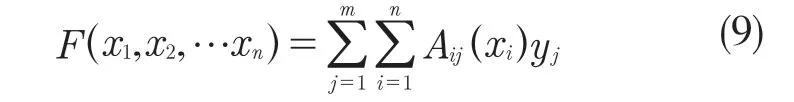
论域Xi(xi)=[-αi(xi)Ei,αi(xi)Ei],Y(y)=[-β(y)U,β(y)U]。其中,αi(xi)(i=1,2,…,n)与β(y)分别为输入和输出论域的伸缩因子。
2.2 隶属度函数和数量
为了方便模糊规则的设计具有可解释性,每个输入变量的隶属度函数数量都取3 个,如图2所示。这种只有NE,ZO,PO 的划分十分客观,不依靠人的主观经验,而且这种形式简单,实时性较好。

图2 变论域模糊控制输入隶属度函数Fig.2 Membership function of variable universe fuzzy control input
考虑到控制器要有普遍适用性,对论域进行归一化处理,实际输入论域由量化因子控制,输入实际论域分别为[-1/Ke,1/Ke]和[-1/Kec,1/Kec]。同理,输出论域由比例因子控制,输出实际论域为[-1/Ku,1/Ku]。
在计算模糊系统的输出时,由于推理后件的模糊集只出现它们的峰点,而与隶属函数的形状无关,因此根据上述系统的9 种运动状态,经过归一化处理,得到需要考虑的9 个峰点所对应的值,分别为0,±0.25,±0.50,±0.75,±1.00。
2.3 模糊规则
传统的模糊规则往往模棱两可,不同的控制对象模糊规则可能会不同,影响模糊控制的应用,因此我们需要一种具有普遍适用性的模糊规则。当模糊集数量为3 个时,可以利用阶跃响应来获得模糊规则[7]。
在典型控制系统的阶跃响应中,y(t)是输出响应,r(t)是输入参考值,则误差e(t)=r(t)-y(t)。控制系统的参考输入为1。如图3 中间实横线所示,稳态误差带设定为±10%,即中间横线上下两条虚线之间的范围,由于误差在此范围内绝对值不大,这个范围称为零带,用[-e0,e0]表示。同理,误差变化的零带可用[-ec0,ec0]表示。当输出响应曲线在零带下,我们称误差为正;当输出响应曲线在零带中,称误差为零;当输出响应曲线在零带上,称误差为负。以此类推,误差变化同样也有这3 种情况,那么控制系统的响应情况可以分为9 种情况,这9 种情况如图3 所示。

图3 阶跃响应示意图Fig.3 Diagram of step response
(1)在AB 段,误差为负且有增大的趋势,误差变化为负,即e<-e0,ec<-ec0。为尽快消除已有的负大误差并抑制误差变大,控制量在负方向取最大。
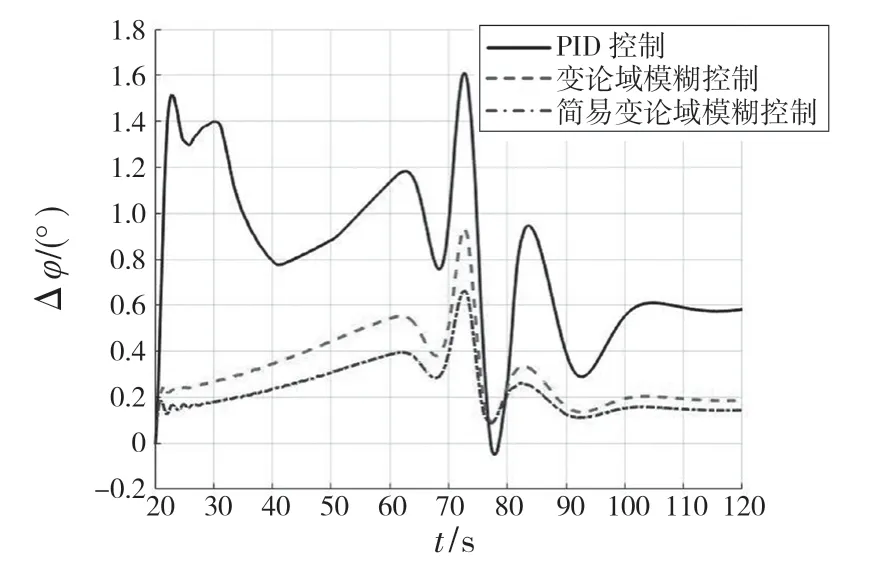
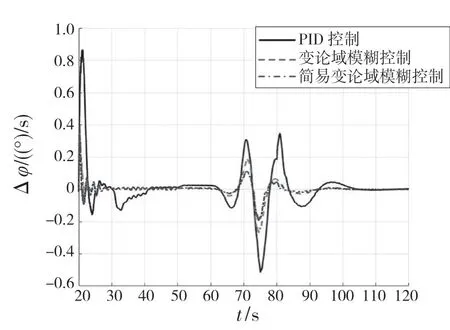
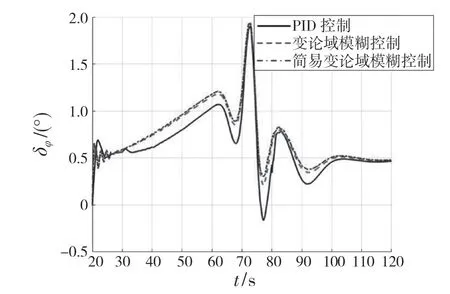
(2)在BC 段,误差为负且变化不大,误差变化处于零带,即e<-e0,ec (3)在CD 段,误差为负且有趋向零带的趋势,误差变化为正,即e<-e0,ec>ec0。此时控制量取在负方向比BC 段更小的量。 (4)在DE 段,误差在零带内且有向正向变大的趋势,误差变化为正,e (5)在EF 段,误差为正且有增大的趋势,误差变化为正,即e>e0,ec>ec0。此时应该在正方向取最大的控制量来抑制这个趋势。 (6)在FG 段,误差为正且变化不大,误差变化处于零带,即e>e0,ec (7)在GH 段,误差为正且有趋向零带的趋势,误差变化为负,即e>e0,ec<-ec0。此时控制量在正方向取比FG 段更小的量。 (8)在HI 段,误差在零带且有负向变大的趋势,误差变化为负,即e (9)在IJ 段,误差在零带且变化不大,误差变化也处在零带,即e 基于以上分析,可以得到客观、简单、完善且具有解释性的模糊规则,如表1 所示。 表1 变论域模糊控制规则Tab.1 Variable universe fuzzy control rules 文献[4]仿真结果表明,模糊控制对弹性振动的干扰没有较好的鲁棒性,因此需要设计校正网络。传统的校正网络设计工作量大,而且需要一定的设计经验。目前频域设计校正网络除了利用经验设计之外,还有渐近法[8]和粒子群算法[9]。渐进法是根据统计数据,根据几个优化原则,对参数进行多次修正,该方法应用导弹获得较好的效果,但对于运载火箭刚体、晃动、弹性体严重耦合的情况,该方法并不适合。而在文献[9]中,利用粒子群算法对抑制弹性振动的陷波器参数进行优化设计,并未考虑贮箱晃动,因此需要一种粒子群优化算法来同时实现对贮箱晃动和弹性振动的抑制。 以主动飞行段第60 s 特征秒为例,主动段的未校正开环传递函数伯德图曲线基本上与图4 的未校正传递函数伯德图曲线相似,可以设计同一种形式的校正网络,只需要调整校正网络参数即可,因此校正网络的设计问题转化为参数优化问题。校正网络设计的目标是保证运载火箭刚体、晃动、振动稳定且具有一定的稳定鲁棒性。这也就是要求刚体高频幅值、刚体相位,晃动幅值以及弹性振动幅值具有一定稳定裕度[10]。校正网络传递函数形式为 图4 运载火箭姿态控制系统裕度综合图Fig.4 Margin synthesis diagram of attitude control system of launch vehicle 式中:第1 分式和第2 分式构成的陷波器能够对晃动进行幅值稳定,第3 分式对1 阶弹性振动进行相位稳定以及对2 阶以上的弹性振动进行幅值稳定,第4 分式对2 阶弹性振动进行幅值稳定。 (1)设计目标:刚体高频幅值裕度为8 dB,刚体相位裕度为35°,晃动幅值裕度为6 dB,2阶及2 阶以上的弹性振动幅值裕度都为8 dB。刚体截止频率的大小影响系统的响应速度,因此要尽可能保证校正后的截止频率接近校正前的截止频率。 (2)约束条件: ①为了减少优化时间,校正网络参数也应该限制搜索范围。根据设计经验,ω11应该略小于ωh1,一是可以避免滤波器对刚体截止频率的影响,二是可以尽可能衰减频率为ωh1的幅值; ②ω21应略大于ωh2,以确保频率为ωh2和ωh3的幅值都能小于幅值裕度; ③ω31应介于10 Hz 和一阶振动频率之间,一来可以保证一阶弹性振动的相位低于180°,二来可以对4 阶弹性振动幅值造成足够的衰减; ④ω41则确保在二阶弹性振动频率附近; ⑤至于ζi1和ζi2(i=1,2,4),ζi1一般在0.1和1 之间,ζi2在0.01 和0.1 之间; ⑥由于校正后的稳定裕度并不一定会完全等于目标裕度,可能会小于目标,因此需要要求校正后的各个目标频率的幅值要大于幅值裕度,相位也要大于相位裕度。 式中:ωc——校正后刚体截止频率;ωc0——校正前刚体截止频率;ωN——刚体第2 次穿越频率;ωh1,ωh2,ωh3——晃动幅值最大的3 个频率;ω2——2 阶弹性频率;ω4——4 阶弹性频率。 最终得到该特征秒的滤波器参数: 如图4 所示,此时刚体截止频率ωc=2.146 1 Hz,而ωc0=2.231 0 Hz,M(ωc)=38.153 4°,GM(ωh1)=-12.3 dB,GM(ωh2)=-14.9 dB,GM(ωh3)=-7.37 dB,GM(ωh3)=-7.06 dB,GM(ωN)=16.197 3 dB,PM(ω1)<180°,GM(ω2)=-16.3 dB,GM(ω4)=-15.3 dB,符合设计要求。 基于此方法,可以对主动段各特征秒的校正网络参数进行快速优化设计。 PD 控制、变论域模糊控制和简易变论域模糊控制在额定状态下的仿真结果如图5—图7 所示。简易变论域模糊控制参数:ke=32,kec=20,ku=0.17,α1(x1)=│x1/32│0.01,α2(x2)=│x2/20│0.01,β(u)=│u/0.17│0.01。 从图5、图6 可以看出,简易变论域模糊控制的动态性能要好于变论域模糊控制和PD 控制。简易变论域模糊控制、变论域模糊控制和PD 控制在大风区的最大姿态角偏差分别为0.662 0°,0.930 1°,1.610 3°。其中简易变论域模糊控制的姿态角偏差比PD 控制的姿态角偏差小58.89%,比变论域模糊控制姿态角偏差小28.82°,一方面说明简易变论域模糊控制在控制精度上有明显优势,另一方面基于客观模糊规则的控制性能上要优于基于主观经验模糊规则的控制性能。 图5 俯仰角偏差变化Fig.5 Change of pitch angle deviation 图6 俯仰角速度变化Fig.6 Change of pitching angular velocity 从图7 可以看出,简易变论域模糊控制、变论域模糊控制和PD 控制在大风区的最大发动机摆角分别为1.940 7°,1.931 8°,1.899 0°。这3种控制方法的发动机摆角最大相差2.2%,也就是在说发动机提供的控制力矩相差不大的前提下,但是基于简易变论域模糊的姿态角偏差却比基于PD 控制的姿态角偏差小58.89%,这说明简易变论域模糊控制对外扰动的鲁棒性较好。 图7 发动机摆角变化Fig.7 Change of engine swing angle 本文研究了基于简易变论域模糊控制的运载火箭姿态控制设计,改进了变论域模糊规则的设计。对校正网络的设计进行了改进,利用粒子群算法优化设计校正网络参数,实现对贮箱晃动和弹性振动信号的过滤。仿真结果表明:简易变论域模糊控制对外部干扰具有较好的鲁棒性,并且控制精度比PD 控制要高。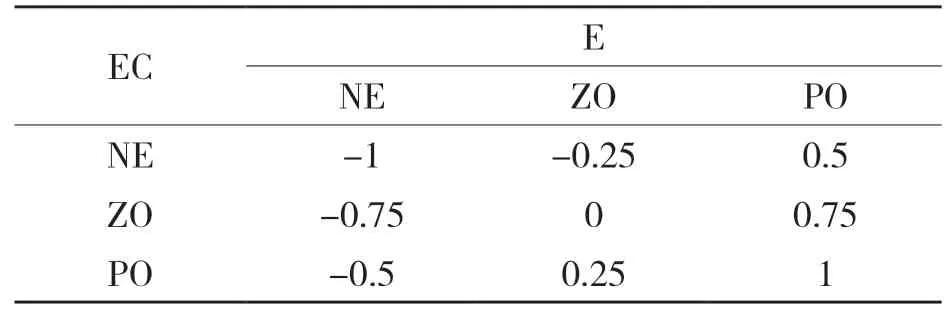
3 校正网络设计
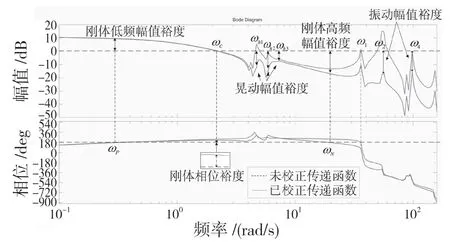



4 仿真结果与分析
4.1 仿真结果
4.2 结果分析
5 结语
