分布式主/被动成像探测系统目标空间协同定位方法研究
2021-12-28顾一凡赵文龙唐善军杨擎宇
顾一凡,赵文龙,唐善军,杨擎宇,郑 鑫
(1.上海机电工程研究所,上海 201109;2.上海航天技术研究院,上海 201109)
0 引 言
随着图像处理技术的发展以及数据通信能力的提升,分布式成像探测系统逐渐成为精确制导武器系统中的重要组成部分[1]。分布式成像探测系统能够从跨场景、跨平台、多视角、多粒度地提取目标信息,包括目标图像信息(纹理、形状、灰度等)、目标运动信息以及目标方位位置信息等[2]。
分布式成像探测系统为了保证系统在复杂战场环境下的可用性及鲁棒性,常使用多种体制的成像探测器构成分布式成像探测系统,包括可见光、红外及合成孔径雷达(synthetic aperture radar,SAR)成像探测器,从成像源特性可以分为可见光、红外被动成像探测器和SAR 主动成像探测器。分布式主/被动成像探测系统是指各平台仅搭载主动或被动一种成像探测器所组成的分布式系统,其主要任务是通过不同平台上的不同成像探测器对目标空间位置进行融合解算。不同特性的成像探测器由于其成像模型不同,在已知目标像素位置的前提下对其三维信息进行求解,其三维信息量与解算方式都各不相同。因此,在对分布式主/被动成像探测系统探测到的目标进行空间协同定位时,需要通过构建统一的空间协同定位解算模型,并用统一的算法解算出目标三维空间位置。
针对上述问题,本文在可见光、红外、SAR 主/被动成像探测器的应用背景下,构建一种结合了共线方程与距离-多普勒方程的目标协同空间定位数学模型,该模型为分布式主/被动成像探测系统提供了统一的目标空间位置解算框架;并采用线性加权-遗传算法来对统一的数学模型进行解算,解决了主/被动成像探测器带有不同定位误差时的目标空间协同定位问题。
1 主/被动成像系统目标空间定位数学模型
分布式主/被动成像探测系统首先需要完成对不同体制成像系统目标空间定位模型的搭建,本文主要研究可见光/红外被动成像系统以及SAR主动探测系统。由于其成像机理不同,主/被动成像探测系统所常用的成像模型也大不相同。本文对于可见光/红外被动成像系统采用相机针孔模型,对于SAR主动成像系统采用线性距离-多普勒模型,在此基础上搭建主/被动成像探测系统的目标空间定位数学模型,从而分别完成目标像素信息到空间信息的转化[3-5]。
1.1 基于共线方程的被动成像目标空间定位数学模型
可见光/红外被动成像探测系统通过相机针孔模型[6]对目标进行成像,但单个探测器无法获得目标的径向距离信息,即被动成像探测系统只能获得与目标之间的相对方位、俯仰角信息。
因此,本文通过共线方程法[6],即根据“目标物点-目标像点-探测器点”三点共线,构建被动成像探测系统的目标空间定位数学模型,即线性共线方程组。共线方程法流程如图1所示。
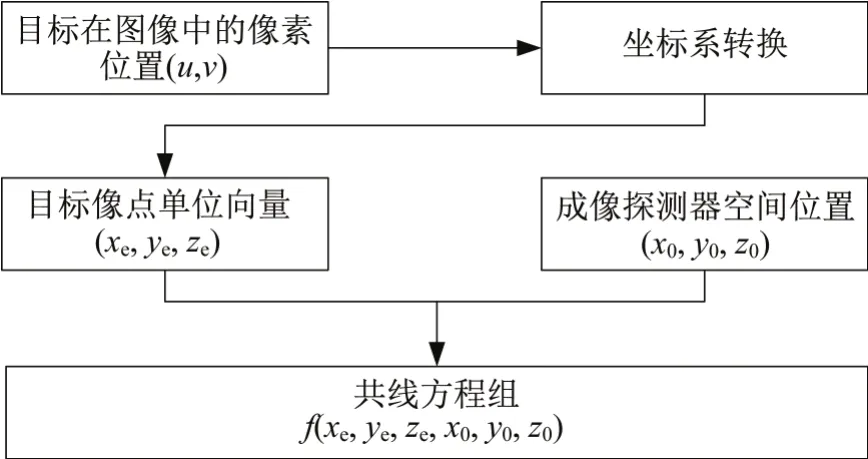
图1 共线方程法流程Fig.1 Collinear equation method process
根据图1 所示,基于共线方程法的目标定位数学模型主要通过如下步骤构建:
1)由于缺少目标径距信息,只能从目标的图像像素信息中提取目标像点单位向量坐标,通过一系列坐标系转换[7-12],将目标的像素位置(u,v)从图像像素坐标系转换到世界坐标系下的目标像点单位向量位置(xe,ye,ze)。
目标像点单位向量在被动成像探测器成像模型中的定义如图2所示。
图中:Ot为光心;OtXtYtZt构成相机坐标系;左平面为被动成像探测器的成像平面;成像平面中心Ou与光心Ot之间的距离称为焦距fc;成像平面上的点T0为目标成像点。假设存在一个虚拟成像平面,即图2 中的右平面,T为目标在三维世界坐标系中的位置,T、T′、光心Ot以及目标成像点T04 点共线。因此,可以根据共线与坐标系转换关系,得到目标像点单位向量(xe,ye,ze)在世界坐标系下的位置为
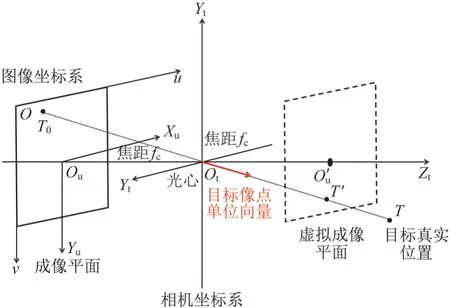
图2 目标像点单位向量示意图Fig.2 Schematic diagram of target image spot unit vector
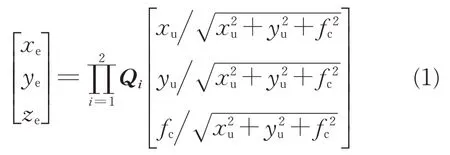
式中:(xu,yu)为目标像点在图像物理坐标系下OuXuYuZu的Xu轴、Yu轴坐标;fc为相机焦距。(xu,yu)的计算方式如下:

式中:(u,v)为目标在图像中的像素位置;(u0,v0)为图像上的(0,0)点在图像像素坐标系下的位置坐标;dx和dy表示横向以及纵向的像元尺寸。
式(1)中的Qi(i=1,2)为相机坐标系到世界坐标系的转换阵[7-12],主要通过成像姿态角、平台姿态角计算得到,主要计算方式如图3所示。
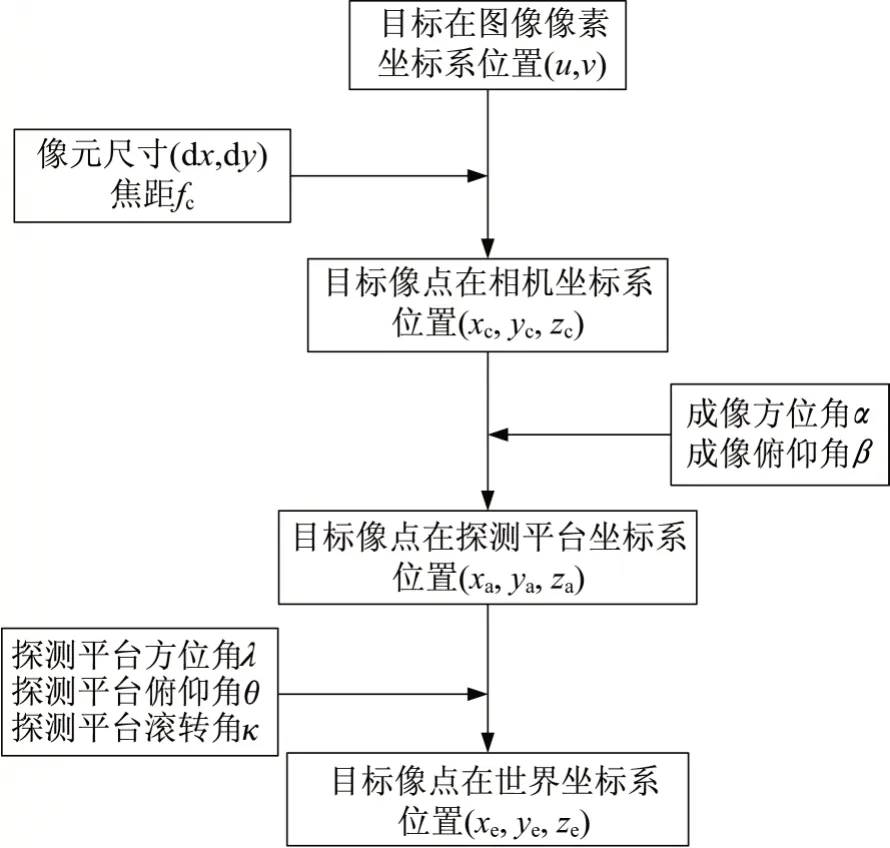
图3 坐标系转换过程Fig.3 Coordinate system transformation process
其中,各坐标系之间的转换矩阵Qi(i=1,2)定义如下:
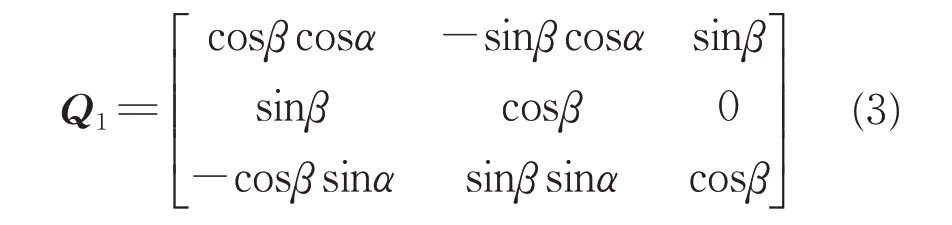

式中:(α,β)为成像探测器的成像方位角及俯仰角;(λ,θ,κ)为探测平台的方位、俯仰及滚转角。
2)已知目标像点、成像探测器在地理坐标系下的空间位置,根据空间中两点确定一条直线原理,可以得到目标视线方程为
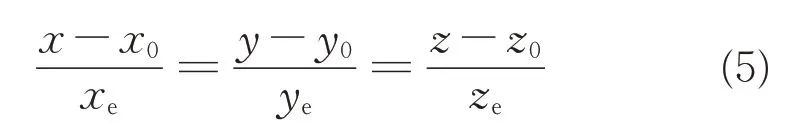
式中:(x0,y0,z0)为成像探测器在世界坐标系下的空间位置;(xe,ye,ze)为目标像点单位向量在世界坐标系下的空间位置。
将式(5)直线方程转化为参数方程

式中:t为空间直线参数方程中的参数。
根据上述两个步骤可以获得被动成像传感器的共线方程(组),该方程组由4 个未知数构成,因此只有当2 个以上的被动成像传感器构成的共线方程(组),才能解算出目标在世界坐标系下的空间位置。
1.2 基于距离-多普勒(RD)算法的主动成像目标空间定位数学模型
本文主要研究合成孔径雷达(synthetic aperture radar,SAR)主动成像探测系统[13-14]。对于该类型成像探测系统,采用聚束式SAR成像模式能够在较小的范围内进行目标探测,且该成像模式成像分辨率较高[15]。通过聚束式SAR 成像模式可以将原始雷达数据进行方位和距离向成像,形成SAR 图像,获得目标的多普勒及距离信息,以便后续对目标空间位置进行解算。
SAR 主动成像探测系统常使用距离-多普勒(range-Doppler,RD)算法构建目标空间定位数学模型,即非线性RD方程组,其流程如图4所示。
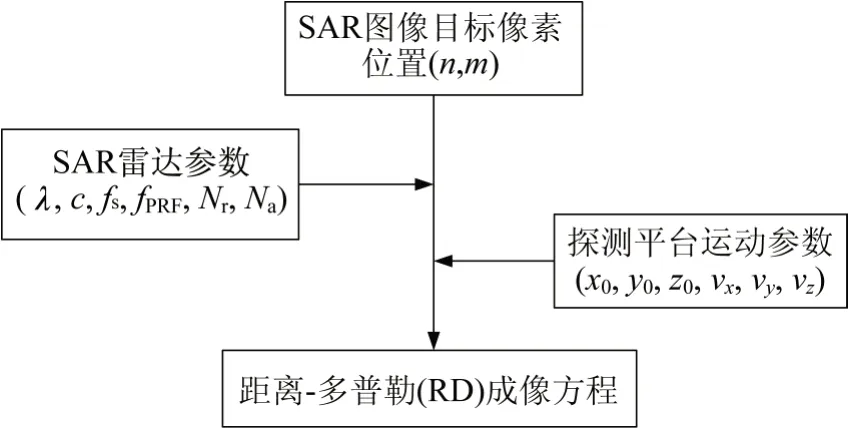
图4 RD算法流程Fig.4 RD algorithm process
根据图4 所示,基于RD 算法的目标定位数学模型[13]主要通过如下步骤构建。
1)由于原始雷达数据已知,可以根据SAR 图像上的目标像素位置、方位及距离向采样点数等图像物理信息以及雷达波速、采样频、脉冲频率等雷达辅助信息,构建目标的径距与多普勒量测方程
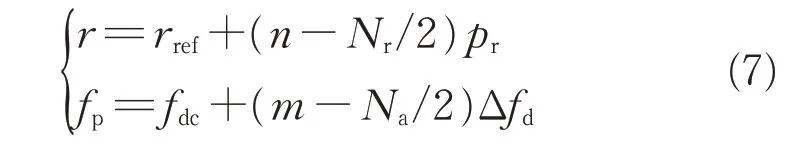
式中:rref为成像参考点到飞行平台在成像时刻空间位置之间的距离;(n,m)为目标点P 在SAR 图像上的距离向像素坐标、方位向像素坐标,其单位为像素(pixel);Nr为距离向SAR 图像采样点数;Na为方位向SAR图像采样点数;pr为SAR图像中距离向坐标中每个像素所代表的实际径距量测;fdc为成像参考点的多普勒频率,其计算方式为
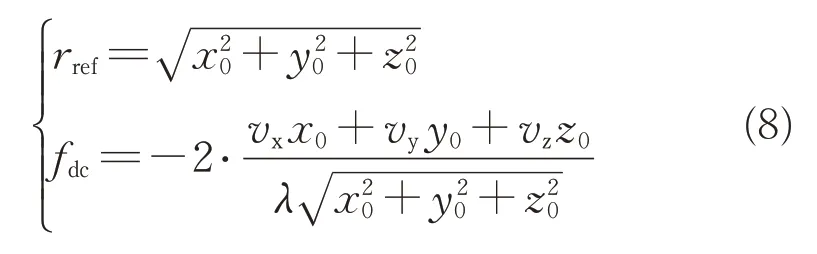
Δfd为SAR 图像的方位向坐标中每个像素所代表的实际多普勒频率量测,其计算方式为[13]
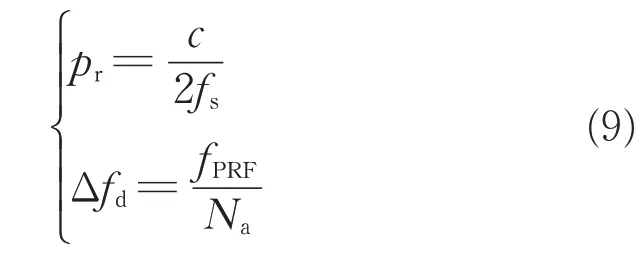
式中:c为SAR 雷达波速;fs为SAR 雷达信号采样频率;fPRF为SAR 雷达脉冲频率;Na为方位向SAR 图像采样点数。上述雷达辅助参数都是由SAR 传感器提供。
2)结合SAR 主动成像探测系统空间位置及运动速度,联立多普勒频率计算公式,构建目标径距与多普勒量测方程
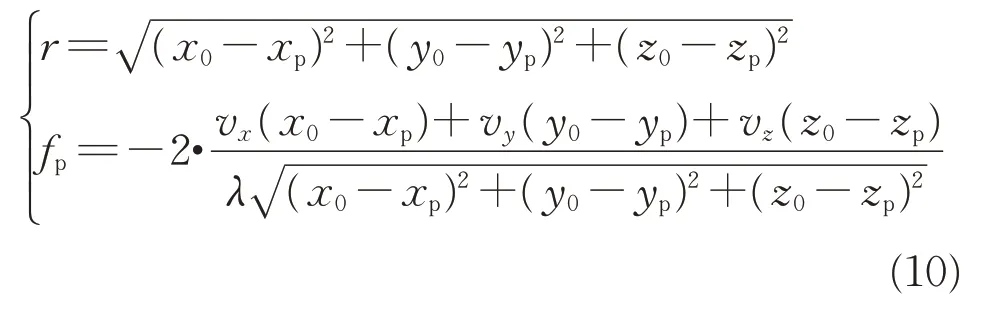
式中:(r,fp)为式(7)中求得的目标径距及多普勒量测;(x0,y0,z0)为SAR 主动成像探测系统在成像孔径中心时刻的位置;(vx,vy,vz)为探测系统在世界坐标系下运动的各轴速度分量;λ为雷达波长。
根据以上两个步骤,可以获得主动成像传感器的距离-多普勒(R-D)方程(组),该方程组由3 个未知数构成,且为非线性方程组,因此只有当2个以上的主动成像传感器构成的R-D 方程(组),才能解算出目标在世界坐标系下的空间位置。
2 分布式主/被动成像探测系统目标空间协同定位方法
根据1.1 节及1.2 节对主动及被动成像探测系统的目标空间定位数学模型的构建,可以发现:对于单个被动成像探测器,其目标空间定位的实质是求解由共线方程算法构建的线性方程组;对于单个主动成像探测器,其目标空间定位的实质是求解由距离-多普勒(R-D)算法构建的非线性方程组。
由于单个主/被动成像探测器无法求解线性/非线性方程组的唯一解,因此使用分布式主/被动成像探测器构成的成像探测系统能够对线性及非线性方程组进行综合求解,得到唯一的目标空间协同定位结果。本文提出一种分布式主/被动成像探测系统目标空间协同定位数学模型,并采用线性加权-遗传算法来对该数学模型进行解算,解决两个以上分布式主/被动成像探测器的目标空间协同定位问题。
2.1 分布式主/被动成像探测系统目标空间协同定位数学模型
分布式主被动成像探测系统目标空间协同定位数学模型是由1.1 节及1.2 节中基于共线方程的被动成像目标空间定位数学模型与基于距离-多普勒(RD)方程的主动成像目标空间定位数学模型所联立构成的非线性方程组,其形式如下:

式中:fdetectori(·)(i=1,2,…,N)代表探测器detectori的成像方程;N为图像传感器总数;fdetectori(·)中的(x,y,z)为目标的空间位置;(ui,vi)为目标在图像上的像素位置;parameteri为辅助解算空间位置的探测器及雷达相关参数。若detectori为被动成像探测器,则fdetectori(·)为3 个线性方程构成的共线方程组,若detectori为主动图像传感器,则fdetectori(·)为两个非线性方程构成的R-D方程组。
分布式主/被动成像探测系统(可见光/红外/SAR)的空间目标协同问题可以转化为线性与非线性混合方程组的求解问题。而由于各探测器噪声的存在,上述方程组会转化为

式中:Δεi(i=1,2,…,N)为成像探测器的定位误差。
在求解上述带有噪声项方程组的过程中,会出现求解算法收敛缓慢或者失效的现象。因此本文针对带有噪声的图像传感器的空间协同目标定位问题,将该方程组的求解问题转化为最优化问题来求解。
本文提出的分布式主/被动成像探测系统的目标空间协同定位模型的最优化目标函数如下:
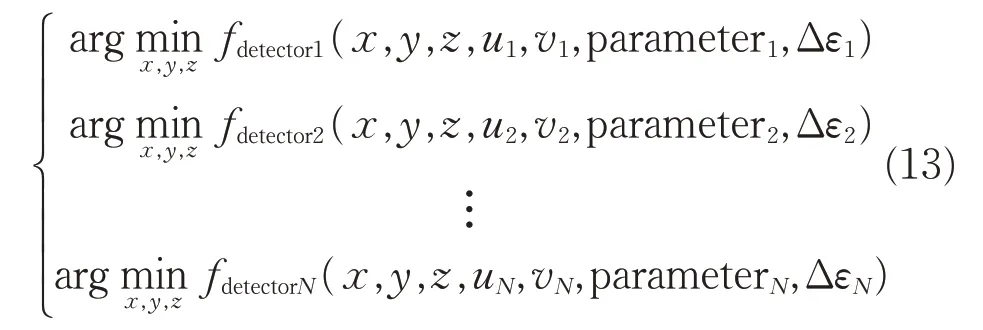
最优化问题目的是求取使式(13)达到最小值情况下的(x,y,z),以此作为分布式主/被动成像探测系统最终的目标空间协同定位结果。由式(13)不难发现,上述问题是一个多目标优化问题,即需要同时保证上述每个目标函数在(x,y,z)点取到最小值,才能获得全局最优的估计。
本文构建的目标空间协同定位模型是面向分布式平台、多源主/被动成像探测器的目标空间定位系统,不同于交叉定位系统或雷达定位系统,其对两者进行了综合,本质是综合了线性方程组定位模型与非线性方程组定位模型的数学模型架构。
2.2 基于线性加权-遗传算法的目标空间协同定位求解方法
遗传算法(genetic algorithm,GA)是一种启发式的优化搜索算法,针对最优化问题,通过编码、初始化种群、评估适应度、选择、交叉及变异步骤[16],其算法优势在于能够不受优化函数的连续性限制,可以在全局范围能进行目标函数的优化搜索,同时也可以自动地调整优化和搜索的方向,算法速度较快。其步骤流程如图5所示。

图5 遗传算法流程示意图Fig.5 Schematic diagram of genetic algorithm
1)编码:编码方式有二进制编码法、符号编码法以及浮点编码法。
2)参数设定:遗传算法需要对各步骤的参数进行预先设定。
3)初始种群:遗传算法在运行前需要先对初始种群进行设定,主要确定其规模和个体数量。
4)构建适应度函数:遗传算法的重点在于适应度函数的构建,本文通过上节分布式主/被动成像探测系统的目标空间协同定位的目标函数数学模型来构建适应度函数。
5)选择:选择的目的是将种群中能够达到适应度的个体选取出来,将其作为后代种群,选择规则需要结合个体在种群中的分布情况,未被选择的种群个体需要被该种群淘汰。
6)交叉:交叉的目的是在种群中的个体之间利用染色体运算规则,使得该种群能够向目标函数的优化方向遗传进化。
7)变异:变异的目的是多样化种群中的个体,防止种群在遗传进化过程中陷入局部最优。
由于在实际应用过程中,各主/被动成像探测器都带有定位误差,因此,将根据主/被动成像探测器的定位误差来源,对各个探测器对应的目标函数进行权重选取,即对带有不同定位误差的主/被动成像探测器赋予不同的权重,利用线性加权法,将多目标函数优化问题转换为带权重的单目标函数优化问题。本文基于线性加权的目标函数形式如下:

式中:wi为各主/被动成像探测器对应的权重因子,可根据不同定位误差设定不同权重构建优化模型对目标空间位置进行求解。
在线性加权目标函数的基础上,利用遗传算法求解该单目标优化问题,完成分布式主/被动成像探测系统的目标空间协同定位任务。
3 实验结果及分析
本文需解决的分布式主/被动成像探测系统的目标空间协同定位问题在2.1 节转化为对非线性方程组的求解问题。最小二乘求解方法、交叉定位求解方法等方法只能解决被动成像探测系统的线性协同定位问题,无法应用到主/被动成像探测系统。遗传算法能够通过启发式方法解算非线性数学模型,从而解决主动成像探测器的非线性定位求解问题。此外,本文设定分布式主/被动成像探测系统的仿真环境,验证线性加权-遗传算法相较于传统遗传算法在带有不同定位误差的探测系统下的协同定位精度。
仿真实验设定4个主/被动成像探测器构成的探测系统。4个成像探测器的具体情况为:在世界坐标系下,探测器1的空间位置为(15 000 m,15 000 m,4 000 m),探测器2的空间位置为(9 876.4 m,-27 175 m,8 000 m),探测器3的空间位置为(14 000 m,1 000 m,3 000 m),探测器4的空间位置为(-25 856 m,-12 941 m,8 000 m)。目标的真实空间位置为(-300 m,-300 m,0 m)。在上述平台位置、目标位置的条件下,仿真环境如图6所示。
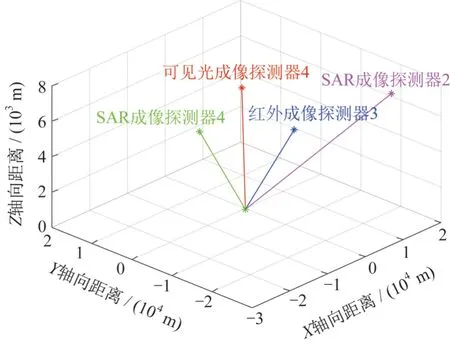
图6 分布式主/被动成像探测系统仿真环境示意图Fig.6 Simulation diagram of distributed active/passive imaging detection system
探测器1 为可见光被动成像探测器,其带有均值为0、方差为20的像素噪声;探测器2为SAR主动成像探测器,其带有均值为0、方差为2的像素噪声;探测器3 为红外被动成像探测器,其带有均值为0、方差为20的像素噪声;探测器4 为SAR 主动成像探测器,其带有均值为0、方差为2的像素噪声。
根据上述成像探测器的误差来源,计算在该水平误差来源下的定位误差,根据成像探测器引起的定位误差的倒数进行线性加权并归一化处理,即该分布式主/被动成像探测系统目标空间协同目标定位模型更加信任定位误差较小的成像探测器,定位误差越小,探测器权重越大。各成像探测器定位误差、来源及探测器权重如表1所示。

表1 各成像探测器定位误差、来源及探测器权重Tab.1 Positioning error,source and detector weight of each imaging detector
仿真实验进行500 次Monte Carlo 仿真,得到线性加权遗传算法与传统遗传算法下的x、y、z轴定位误差的比较结果,如图7(a)~(c)所示。

图7 线性加权与传统遗传算法各轴协同定位误差比较Fig.7 Comparison between linear-weighted genetic algorithm and conventional genetic algorithm
从上述x、y、z轴的定位误差比较结果可知,带权重的目标函数结合遗传算法求解的分布式主/被动成像探测系统的目标空间协同定位结果,其定位误差相较于传统遗传算法较小,两者定位误差的均值与方差如表2所示。
由表2 结果发现,采用线性加权-遗传算法对本文提出的分布式主/被动成像探测系统目标空间协同定位模型进行解算,能够更好地降低带不同等级噪声的主/被动成像探测器在目标空间协同定位时的定位误差,在一定程度上提高了分布式主/被动成像探测系统在目标空间协同定位时的精度。

表2 线性加权-遗传算法与传统遗传算法定位误差比较Tab.2 Comparison of positioning error between linearweighted genetic algorithm and conventional genetic algorithm
4 结束语
分布式成像探测系统在精确制导领域逐渐向体系化、多源化方向发展。本文在多源成像体制下,提出一种分布式主/被动成像探测系统目标空间协同定位模型,解决了成像探测系统在已知目标像素位置的前提下协同解算目标三维空间位置的问题,同时,采用线性加权-遗传算法对本文构建的目标空间协同定位模型进行解算,并与传统遗传算法求解结果进行了比较。仿真试验结果表明,本文所采用的线性加权-遗传算法的目标空间协同定位解算方法能够解决分布式成像探测系统中不同成像探测器带有不同定位误差所带来的定位精度下降的问题,一定程度上提高了该系统整体的目标空间协同定位精度。该技术能够应用于分布式无人机集群、分布式巡航导弹群以及分布式战斗机集群对重要目标的探测任务,提高系统对重要目标的精确探测、打击、拦截能力[17-18]。
