基于Dropout方法的高精度畸变标定方法

金光瑞，王爱华，李 聪，孙吉福

（1.天津津航技术物理研究所，天津 300000；2.上海机电工程研究所，上海 201109）

0 引 言

星敏感器是目前测姿精度最高的探测器，在飞行器和空间飞行器上都有应用［1］。星敏感器光学畸变误差标定的精度直接影响了星敏感器的精度，需要在使用之前对星敏感器光学畸变进行高精度的校正［2-4］。

在工程应用中，星敏感器需要借助二维高精度转台和星模拟器来实现室内标定试验：通过二维转台控制星敏感器在不同俯仰角、不同航向角下对星模拟器成像，采集大量的标定点数据，然后利用基表标定算法进行标定，以实现对星敏感器的高精度标定［5-8］。实际应用中，采集标定点数量不会较多，一般采集的标定点数量为49 个，采用其中25 个标定点用于畸变校正，剩余24个标定点用于测试。而星敏感器模型有20个参数，采用25 个标定点对20 个参数进行拟合，存在过拟合现象，会造成畸变标定结果误差较大。

针对该问题，本文提出一种基于Dropout方法［9-12］的星敏感器畸变模型标定方法。该方法首先对星敏感器高阶曲面畸变模型进行网络化，然后构建隐藏部分卷积层的星敏感器畸变模型，最后进行监督学习，完成星敏感器畸变模型标定，以提高畸变模型的标定精度，提高星敏感器输出的姿态精度。

2 星敏感器畸变模型及标定方法

2.1 星敏感器高阶曲面畸变模型

理想的星敏感器物理成像模型为小孔成像模型，其成像原理如图1所示。

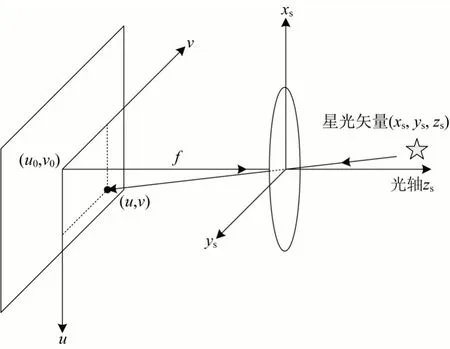
图1 星敏感器小孔成像原理图Fig.1 Schematic diagram of small hole imaging of star sensor

根据其物理模型，可以得到星点坐标（u，v）和星光矢量在星敏感器坐标系中的坐标（x，y，z）之间的关系为

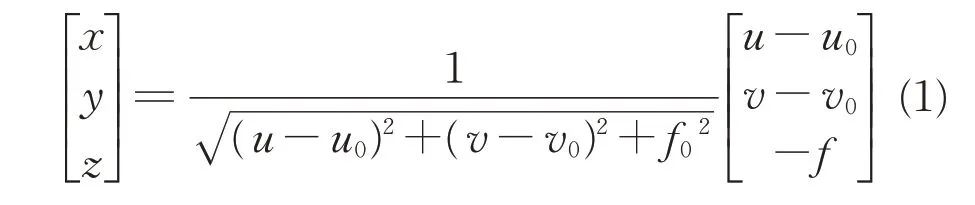
式中：f为星敏感器焦距；（u0，v0）为星敏感器的主点位置。

由于星敏感器光学系统像差、装配误差及焦距误差等因素的存在，星敏感器理论模型与实际情况存在差异，主要包括：CCD 平面上星点的中心位置（u0′，v0′）与理想的星点中心坐标（u0，v0）存在主点误差△d，真实焦距f′和焦距f之间的焦距误差△f，CCD 面阵与理想位置之间存在旋转角β和倾斜角α，此外，还包括光学系统畸变等误差，如图2所示。

图2 星敏感器实际模型Fig.2 Physical model of star sensor

根据星敏感器实际模型还包含许多参数，但这些参数对畸变的影响小于0.1″，可以舍去。因此工程上常用的模型中仅包含主点位置（u0，v0）、焦距f、旋转角β和倾斜角α。这样的模型复杂度较高，可以将模型表示为

式中：主点位置（u0，v0）、焦距f、旋转角β和倾斜角α为常数。

在工程上，式（2）可以表示真实的星敏感器镜头畸变模型。但是其较为复杂，拟合过程难度较大，因此我们采用高阶曲面来描述Fx和Fy函数，将上述模型简化为

式中：（x，y，z）为星敏感器坐标系矢量；（u，v）为星点坐标；N为畸变模型阶数为畸变模型系数。

式（3）即为星敏感器高阶曲面畸变模型。该模型通过20个系数来描述主点位置（u0，v0）、焦距f、旋转角β和倾斜角α等5 个常数，保证了畸变模型的精度；同时采用高阶曲面代替复杂的物理模型，大大简化了标定流程。该方法已在工程上进行了应用，取得了良好的效果。

2.2 星敏感器高阶曲面畸变模型标定方法

星敏感器高阶曲面畸变模型可采用室内标定和外场标定两种方法，由于外场标定受大气影响较大，因此高精度星敏感器一般均采用室内标定。

室内标定需要使用“高精度二维转台＋单星模拟器”。进行室内标定时，利用高精度二维转台控制单星模拟器和星敏感器之间的位置关系，让星敏感器在不同俯仰角、不同航向角条件下采集多个标定点数据，利用这些数据对高阶曲面模型进行拟合，具体过程如下：

1）将星敏感器安装于转台内框架上，调整转台和单星模拟器相对位置，使星敏感器采集的星点处于星敏感器像面中心附近；

2）在视场内设置标定点（一般不少于49 个），由星敏感器测出各标定点的星像数据，并用星点质心算法计算出星像中心（ui，vi），同时记录下转台系统中的俯仰角和偏航角；

3）构建星敏感器畸变标定损失函数，可采用真实星光矢量与畸变模型计算出的星光矢量之间的坐标点误差作为评价标准，据此构建损失函数L为

式中：n为标定网格点总数；（ui，vi）为第i个标定网格点的坐标；（ui′，vi′）为第i个标定网格点的拟合坐标。

采用拟合方法对星敏感器畸变模型进行标定时，存在拟合效果不佳的情况。拟合效果不佳可以分为欠拟合和过拟合。欠拟合是指模型过于简单时，由于训练数据误差大，在无先验知识的情况下，拟合结果不理想，造成欠拟合。过拟合是指模型过于复杂时，因为训练数据不足，导致在训练数据外的测试数据上效果不理想，产生过拟合。拟合效果如图3所示。

图3 拟合效果不佳示意图Fig.3 Indication of poor fitting effect

星敏感器畸变标定过程中，一般采用5 阶以上的高阶曲面模型。但在实际标定过程中，采集的训练数据数量较少，且由于转台误差等因素，训练数据存在一定的误差。因此，对星敏感器畸变模型进行拟合时，存在一种欠拟合与过拟合耦合存在的情况，即训练样本与测试样本误差较大。解决办法主要有优化模型、增加训练数据、训练数据进行筛选、模型集成4种。这4种方法在星敏感器畸变标定过程中均存在一定局限性：优化模型方法、增加训练数据方法针对过拟合有效，但需要牺牲精度、增加工作量，同时无法避免数据误差引起的欠拟合；训练数据筛选方法可在一定程度上解决欠拟合和过拟合的问题，但需要大量的数据和高精度的转台；模型集成方法通过对多个不同模型进行训练，采用加权求和的方法进行拟合，虽然可以抑制欠拟合和过拟合问题，但会引起计算量急剧增加，不适用于对系统实时性要求比较高的系统。

因此，需要研究一种星敏感器畸变标定方法，在满足弹载/星载系统实时性要求的前提下，提高畸变标定精度。

3 基于Dropout 方法的星敏感器标定方法

3.1 Dropout方法

目前，机器学习领域较多采用的是Dropout 方法，可以有效地缓解拟合不佳现象的产生。

Dropout 方法基本原理为：首先在每一次训练过程中，随机地将隐层中的某些节点置零；再对这样的模型进行训练得到结果；然后将多次训练的结果进行整合，得到最终的拟合结果，如图4所示。

电商(商务秘书)场景实验室以培养学生电子商务实务实践应用能力和创新创业能力为目标，由学校提供场地和管理、企业提供工作项目、技术和师资，行业协会提供平台支持，采取校企双制、产教融合、工学一体的培养模式。

图4 Dropout方法示意图Fig.4 Schematic diagram of the Dropout method

由于网络中节点之间存在强相互作用关系，Dropout方法通过减少网络中隐层节点之间的相互作用，使模型鲁棒性更强，减少过拟合现象对精度的影响。

3.2 星敏感器畸变模型网络化

使用Dropout 方法解决星敏感器畸变模型过拟合问题，首先需要将星敏感器高阶曲面模型构建成类似于神经网络的传输网络。

根据2.1 节描述的星敏感器畸变模型，可以将其分为输入层、池化层、卷积层、输出层共4 层网络。输入层包括输入变量i0和i1；池化层为基于输入提取的特征f0、f1、f2…，池化层参数数量由曲面模型阶数确定；卷积层为最简单的乘法加权网络，加权系数为k0、k1、k2…；输出层为加法网络，输出结果o。具体网络结构如图5所示。

图5 星敏感器标定网络模型示意图Fig.5 Network model of star sensor calibration

输入层为数据：包含两个节点，为星点坐标位置信息（u，v）。

池化层为函数：根据输入层的数据计算出相应的输出，以三阶高阶曲面模型为例，星敏感器畸变模型池化层包含10 个节点函数，这10 个节点函数分别为f0（u，v）＝1、f1（u，v）＝u、f2（u，v）＝v、f3（u，v）＝u2、f4（u，v）＝uv、f5（u，v）＝v2、f6（u，v）＝u3、f7（u，v）＝u2v、f8（u，v）＝uv2、f9（u，v）＝v3。

卷积层为数据：以三阶高阶曲面模型为例，该层包含10 个节点，其结构为简单的乘法网络，这10 个节点数据分别为k0、u·k1、v·k2、u2·k3、uv·k4、v2·k5、u3·k6、u2v·k7、uv2·k8、v3·k9。

输出层o为数据：仅包含1 个节点，为星点坐标x或星点坐标y，根据网络，可表示为

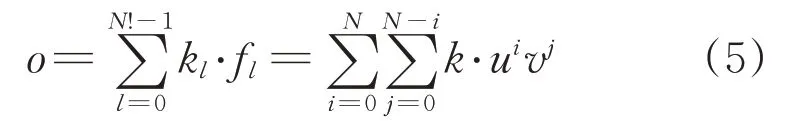
3.3 基于Dropout 方法的星敏感器畸变模型标定方法

利用Dropout 方法对上一节建立的星敏感器畸变网络模型进行拟合，首先要实现对星敏感器模型中的部分卷积层进行隐藏，获得隐藏卷积层的星敏感器畸变模型；然后利用拟合方法对隐藏部分卷积层的星敏感器畸变模型进行监督训练；最后，对训练得到的模型进行整合，获得最终的星敏感器畸变模型。

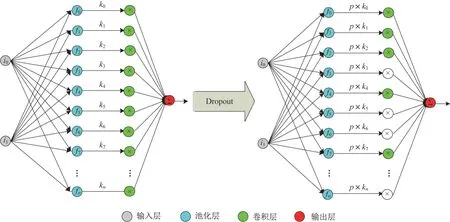
图6 星敏感器标定网络Dropout示意图Fig.6 Dropout model of star sensor calibration network

对星敏感器模型中的部分卷积层进行部分隐藏，可采用调整加权系数的方法。具体方法为将加权系数ki乘以p，p的计算方法为

式中：rand 为［0，1］之间的随机数；thrd 为阈值，一般取0.5。

这样，p的结果为0 或者1 的随机数，可实现对卷积层的随机隐藏，具体隐藏概率可通过阈值thrd 进行调整。需要注意，由于星敏感器模型的特点，一般不对k0、k1、k（2畸变模型中0阶、1阶系数）进行隐藏处理。至此，获得了“隐藏部分卷积层的星敏感器畸变模型”，可用于下一步监督学习。

采用随机的方法生成多个“隐藏部分卷积层的星敏感器畸变模型”，并对每个模型进行训练，统计损失函数Li和模型系数ki。根据式（4）可令损失函数Li为

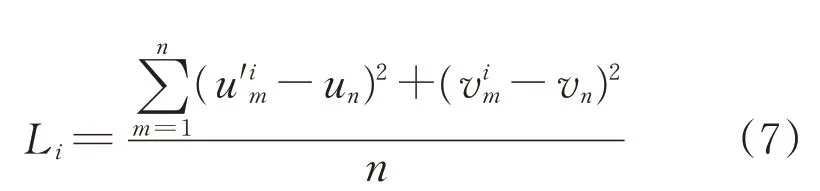
式中：n为标定网格点总数；（um，vm）为第m个标定网格点的坐标为第i个模型中第m个标定网格点的拟合坐标；。

采用式（7）得到的损失函数Li对训练的模型系数ki进行加权，获得最终的模型系数K为

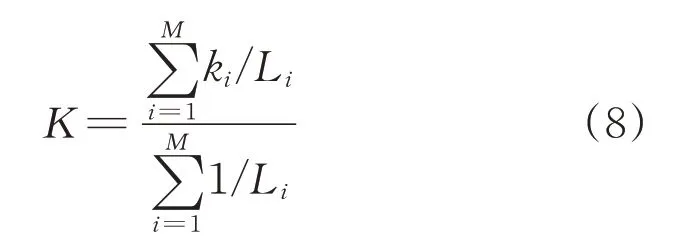
至此，使用Dropout 方法完成对星敏感器畸变模型的标定。

4 试验数据及分析

4.1 真实图像校正试验

采用“转台＋单星模拟器”的方法，进行星敏感器畸变模型校正试验。星敏感器视场为10°×10°，焦距为60 mm，分辨率为2 048×2 048，转台精度3″。

根据星敏感器视场，在视场内按7×7网格采集49个采样点，其中采集25 组数据作为训练数据，24 组数据作为测试数据，具体如图7所示。

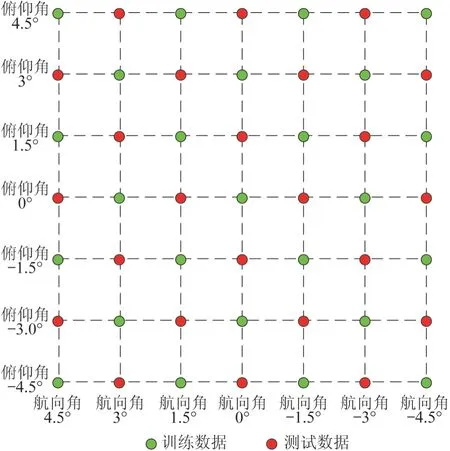
图7 星敏感器标定点网络示意图Fig.7 Point grid of star sensor calibration

畸变模型采用5阶高阶曲面模型，如下所示：

根据模型所示，需要对21×2（x、y每个点21 个系数）共42 个参数进行标定，用于标定的有效数据个数为25×2（25 个点，每个点2 个坐标）共50 个。使用50个数据标定42个系数，存在拟合结果较差的问题。

采用最小二乘修正方法进行曲面拟合，得到训练数据误差、测试数据误差如图8 所示。训练结果最大误差为207.91″、误差均方差为50.78″；测试结果最大误差为167.98″、误差均方差为51.64″。

图8 最小二乘拟合方法训练数据、测试数据误差Fig.8 Training data and test data error using least squares fitting method

采用Matlab 曲面拟合工具箱进行曲面拟合，得到训练数据误差、测试数据误差如图9 所示。训练结果最大误差为8.81″，误差均方差为2.37″；测试结果最大误差为8.13″，误差均方差为2.03″。

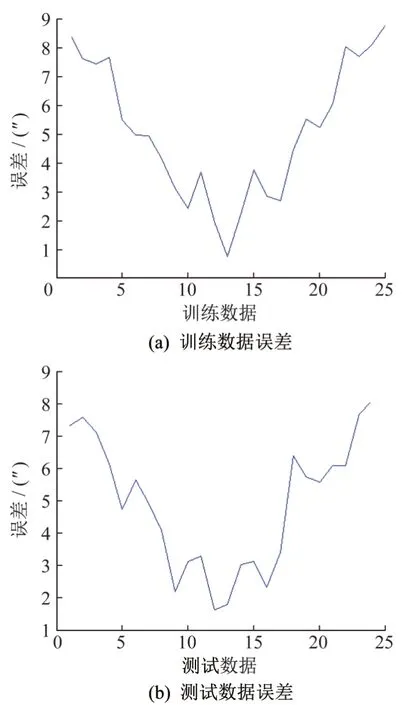
图9 高精度工具箱拟合方法训练数据、测试数据误差Fig.9 Training data and test data error using MATLAb fitting toolbox

采用Dropout 方法进行曲面拟合，得到训练数据误差、测试数据误差如图10所示。训练结果最大误差为0.63″、误差均方差为0.17″；测试结果最大误差为3.65″、误差均方差为1.12″。

图10 Dropout方法训练数据、测试数据误差Fig.10 Training data and test data error using Dropout method

3种拟合方法的误差对比、耗时对比如表1～2所示。

表1 3种拟合方法误差对比Tab.1 Error comparison of three fitting methods

4.2 试验数据分析

从上述图表结果中可以看出：

1）实际采集中，转台误差等因素会造成个别点出现较大误差，而最小二乘法拟合方法对噪声敏感，用该方法进行拟合效果较差。

2）采用拟合工具箱对星敏感器误差进行拟合，可有效降低噪声对拟合结果的影响，提高拟合精度；

3）采用本文提出的基于Dropout方法的高精度拟合方法，相对于工具箱拟合方法，Dropout 方法最大误差精度提高298.4%、平均误差精度提高294.1%，测试数据最大误差精度提高122.7%、平均误差精度提高80.4%，但运算耗时仅增加0.34 ms。

表2 三种拟合方法耗时对比Tab.2 Time-consuming comparison of three fitting methods

5 结束语

本文借鉴神经网络拟合的Dropout思想，提出一种基于Dropout方法的高精度畸变标定方法，构建隐藏部分卷积层的星敏感器畸变模型，完成星敏感器畸变模型标定。试验结果表明，采用基于Dropout方法的星敏感器标定方法可有效提高星敏感器训练精度，相比于高精度工具箱的拟合结果，本文所提出模型的精度提高了80%。