某高速铁路高陡边坡破坏机理及稳定性研究
2021-12-27王衍汇
王衍汇
(中国铁路设计集团有限公司,天津 300308)
在山区进行高铁建设易产生大量高陡边坡,特别是土-岩混合边坡受力机制复杂,对传统的稳定性计算方法提出更高要求[1-2]。王旭结合MP和Sarma法计算混合边坡的稳定性[3];邵帅通过有限元和离散元法对土-岩混合边坡稳定性进行数值计算[4];金磊等基于离散模型试验,开发混合边坡三维细观结构评价模型[5]。该类边坡破坏模式较为复杂,既有土质边坡因土体强度降低、剪应力升高,产生蠕变滑移,导致整体剪切破坏的趋势,又有节理裂隙切割岩体,使其具有不连续性、多变性及各向异性等特点,易导致内部块体沿不利结构面产生平面滑动[6-7]。
鉴于土-岩边坡失稳模式的特殊性,以宣绩高铁某高陡边坡为例,根据其工程地质条件,利用工程地质分析法定性探讨边坡潜在破坏模式,同时结合极限平衡法、块体理论,全面系统分析该边坡的稳定性,为边坡设计提供理论基础。
1 研究区现场调查
1.1 工程地质概况
该高陡边坡位于丘陵地貌,地势总体西北高、东南低,长约130 m,宽约100 m,最大高差约70 m,边坡倾向127°,坡度约40°,线路以半填半挖形式通过山谷冲沟,高陡边坡位于线路右侧,如图1所示。
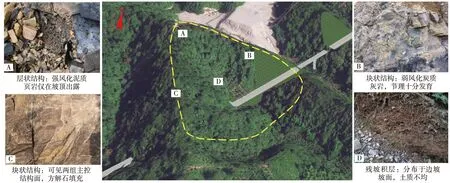
图1 高陡边坡全景
研究区地层主要为第四系残坡积粉质黏土,寒武系中统杨柳岗组强风化泥质页岩,强、弱风化炭质灰岩。其中,粉质黏土土质不均,全风化岩体、角砾土含量约20%;薄层状强风化泥质页岩岩质较软,手掰可断,岩层产状130°∠47°,仅在坡顶出露;强风化炭质灰岩,呈碎块状,层厚1~2.5 m,弱风化炭质灰岩,节理十分发育,岩芯呈短柱状,岩层产状170°∠60°。地下水主要为潜水与基岩裂隙水,赋存于土岩接触面及岩层的层间裂隙、风化裂隙中,地下水稍发育。
1.2 边坡岩体结构调查
通过6个观测点的调查,共获取21组结构面,节理玫瑰见图2。调查区主要发育4组结构面,其中近直立卸荷裂隙(J1)、构造节理(J2)和岩层面(J3)为主控结构面,3组节理裂隙特征见表1[8-9]。
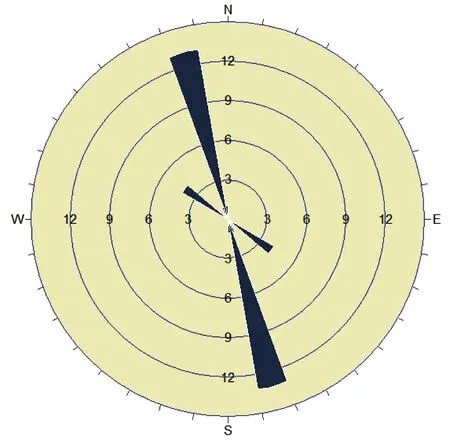
图2 结构面节理玫瑰(走向)

表1 节理裂隙特征
2 边坡潜在破坏模式判别
该边坡由上覆残坡积层与下伏炭质灰岩组成岩体“二元结构”,下伏炭质灰岩具有不透水性,在降雨作用下,易沿土-岩接触面发生整体性圆弧型滑动破坏,如图3。下伏基岩倾向与坡向相同且节理裂隙发育,由赤平投影可知(如图4):①岩层与结构面J1交点C1与边坡投影弧在同一侧,交割线产状为146°∠51.6°,与坡面倾向一致,倾角大于天然坡角,属于稳定结构;②两结构面J1、J2交点C2及岩层与结构面J2交点C3与均边坡投影弧在同一侧,交割线产状分别为169°∠27.8°、91°∠18.9°,与坡面倾向一致,倾角小于天然坡角,属于较不稳定结构,易沿交割线方向发生滑动。由上述分析可知,若上部松散堆积层滑动,则边坡应力重分布,岩体存在平面剪切型、楔型滑动破坏的可能[10-12]。

图3 高边坡潜在破坏模式
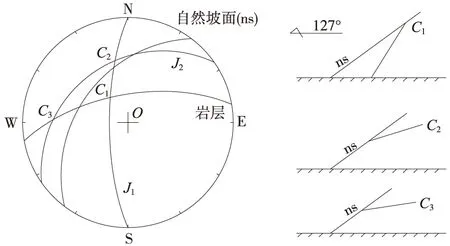
图4 边坡赤平投影及剖面示意
3 边坡稳定性极限平衡分析
3.1 稳定性计算方法
极限平衡法是边坡稳定性分析的传统方法,通过安全系数定量评价边坡的稳定性,该法基于刚塑性理论,注重岩土体破坏瞬间的变形机制,只要求满足力和力矩的平衡、Mohr-Coulomb准则。Morgenstern-Price(M-P)法同时考虑力平衡和矩平衡的变形协调问题,适合任意形状滑动面,计算精度高、实用性好,故采用M-P法建立极限状态方程,如图5[13]。
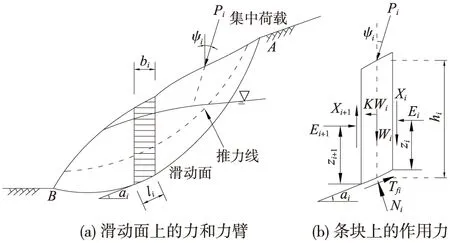
图5 Morgenstern-Price法计算示意
状态函数为
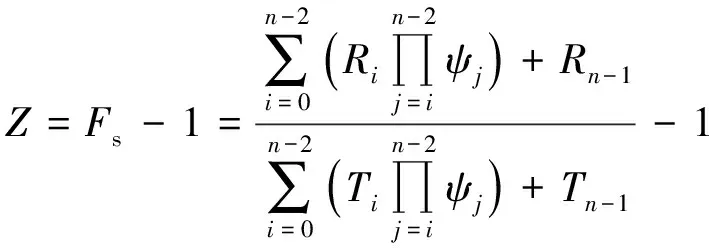
(1)
其中,Ti=Wisinθi+KWicosθi;Ri=(Wicosθi-KWsinθi-Ui)tanφi+cili;ψj=-λf(xj)cosθj-1tanφj-1+sinθj-1tanφj-1/φj+λf(xj)sinθj-1Fs+cosθj-1Fs/φj;
式中,xA、xB分别为滑裂面左右边界坐标,tanαA、tanαB分别为最左端与最右端条块顶面斜率,Fs值可以通过迭代求得,从而得到状态函数表达式。
3.2 稳定性计算
(1)计算剖面
选择具有代表性的剖面为研究对象,边坡地层从上至下依次为:粉质黏土,层厚3~7 m;寒武系中统杨柳岗组强风化泥质页岩,层厚1~5 m;强风化炭质灰岩,层厚2~4 m;弱风化炭质灰岩,未揭穿,剖面如图6所示。
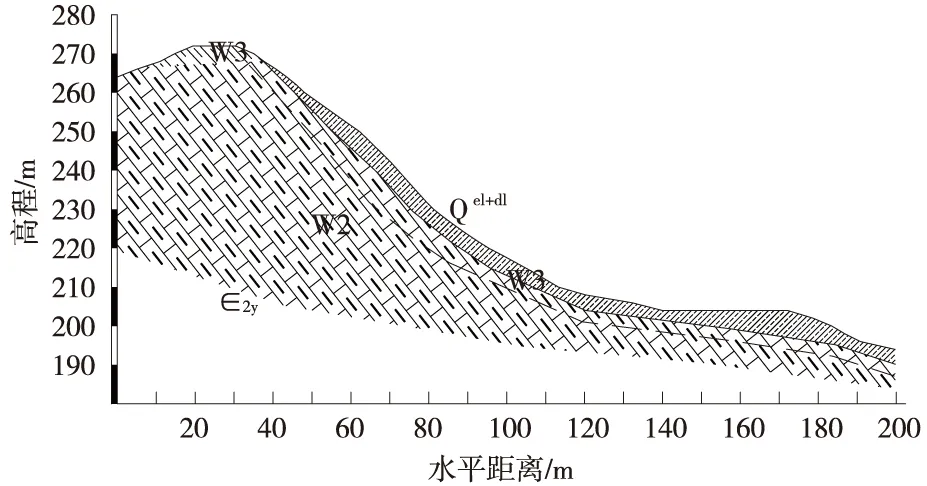
图6 工程地质剖面
(2)计算工况
本地区地震基本烈度为Ⅵ度,根据GB 50330—2013《建筑边坡工程技术规范》5.2.5条:“边坡稳定性计算时,对基本烈度为7度及以上地区的永久性边坡应进行地震工况下边坡稳定性校核”,故不考虑地震作用的影响,仅基于天然工况、暴雨工况进行计算[14]。
(3)计算参数
本次岩土体稳定性计算参数主要依据室内试验,参考GB 50330—2013《建筑边坡工程技术规范》、GB/T 50218—2014《工程岩体分级标准》,并结合现场实际情况、当地经验和类似工程的经验教训综合分析获得[15-16]。岩土体稳定性计算参数建议值见表2。本次取值未考虑岩体节理裂隙的影响,重点分析上部松散堆积物的整体稳定性。
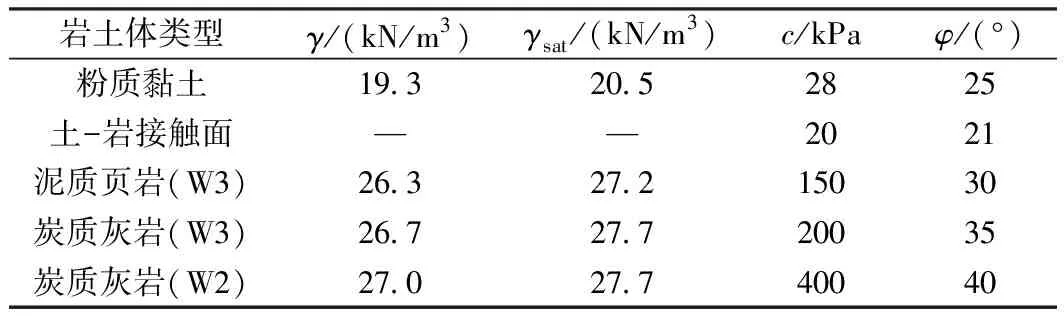
表2 边坡岩土体物理力学参数
3.3 计算结果及稳定性分析
高陡边坡在天然工况、暴雨工况下造成的潜在滑面(M-P法)如图7所示,根据计算边坡在天然工况下稳定系数为1.1,整体处于稳定状态,暴雨工况下稳定系数为1.046,处于极限平衡状态,在降雨作用下残坡积土易沿土-岩接触面发生滑动。
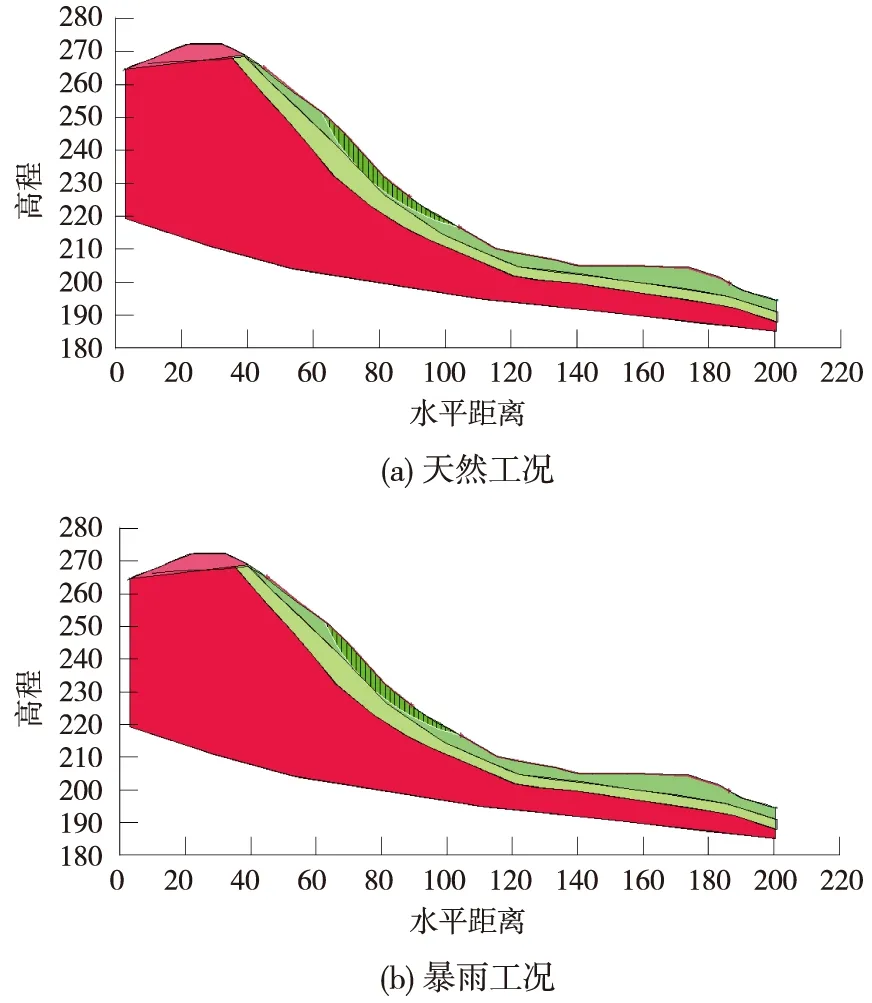
图7 边坡潜在滑面示意(单位:m)
4 基于块体理论的边坡稳定性分析
4.1 块体理论基本原理
块体理论是以岩体完全被节理裂隙切割为前提,包含两个基本定理:块体有界性定理和可移动性定理,这两个定理已经给出了严密的数学推导[17]。
(1)块体有界性定理
设某凸块体由n个半空间的交集构成,将其平移使之通过坐标原点形成棱锥。若棱锥为空,则相应的凸块体有限;棱锥为非空,则相应的凸块体为无限。简明表达式为
JP∩EP=∅或JP⊂SP
(2)
式中,JP为裂隙锥;EP为开挖锥;SP为空间锥。
(2)块体可移动性定理
若由结构面和临空面共同构成的原生块体以及仅由结构面构成的裂隙块体均为有限,则为倒楔块体,即不可动块体;若由结构面和临空面共同构成的原生块体有限,而由结构面构成的裂隙块体无限,则该块体为可动块体,根据稳定状态,可细分为稳定块体、可能失稳块体和关键块体,如图8所示。
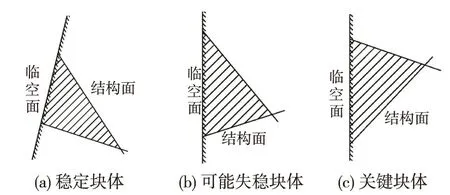
图8 可移动块体分类
利用集合论方法可给出简明表达式,有
JP∩EP=∅且JP≠∅
(3)
基于上述定理,设结构面和临空面为空间平面,结构体为凸块体,用空间向量表达荷载作用,利用几何拓扑学方法分析块体的类型以及块体失稳模式,进而计算块体的稳定性,可得以下两种形式:
(1)平面剪切型滑动,即块体沿单面接触滑动,其安全系数为
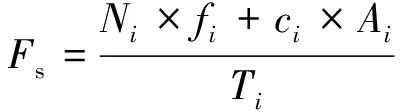
(4)
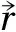
(2)楔型滑动,即块体沿双面接触滑动,其安全系数为
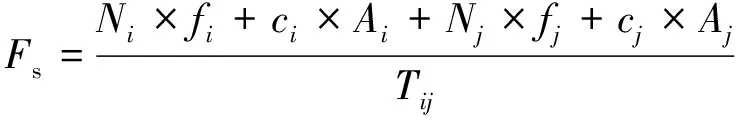
(5)
式中,fi、fj为滑动面i、j的摩擦系数;ci、cj为滑动面i、j的黏聚力;Ai、Aj为滑动面i、j的面积;Ni、Nj为主动力合力在滑动面i、j上沿法向的分量;Ti、Tj为主动力合力在滑动面i、j上沿切向方向的分量。
其中Ni、Nj和Ti、Tj按照下式计算,有
(6)
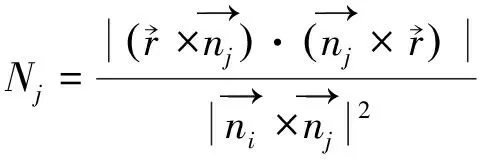
(7)
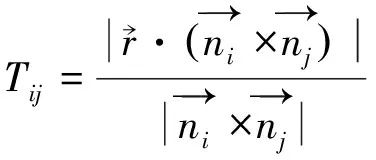
(8)
由前文分析可知,高陡边坡在暴雨工况下处于极限平衡状态,且岩体节理裂隙发育,若上部松散堆积层滑动,则岩体存在平面剪切型滑动破坏、楔型滑动破坏的可能。因此,决定采用块体理论对边坡内部的重点块体进行研究。
4.2 结构面参数确定
室内试验求得的结构面强度未考虑其特性,无法反映裂隙对岩体稳定性的影响,安全系数偏大。而通过现场调查并利用经验公式估算结构面强度参数得到了广泛的应用,其中Barton模型被普遍采用,结构面抗剪强度的经验公式为

(9)
式中,JRC为结构面粗糙度系数;JCS为结构面壁面抗压强度;φb为结构面基本摩擦角;σn为结构面上的有效正应力。
因此,根据结构面现场调查数据,基于Barton模型即可得到结构面与坡面产状及强度指标(见表3)。

表3 结构面与坡面产状及强度指标
4.3 可动块体判断
选取半径R=1的参考圆,圆心为赤平投影直角坐标系的原点,设东向(E)为x轴正值,北向(N)为y轴正值。那么可得半径为r、圆心坐标为(Cx,Cy)的投影圆Pi(见表4)。

表4 投影圆Pi的几何信息
根据各结构面的产状信息绘制投影圆形成如图9所示的边坡各平面投影。由图9可知,在平面投影图中裂隙锥(SP)属于P4投影圆的内域。根据块体理论可得边坡可动块体为JP000。
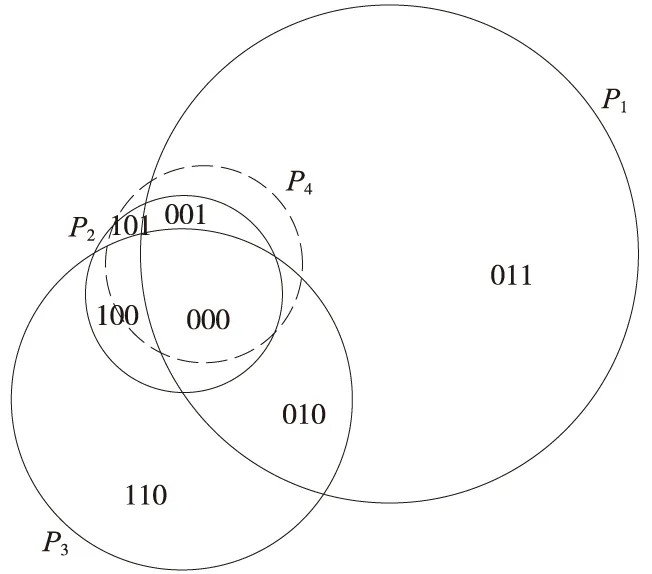
图9 边坡各平面投影
4.4 可移动块体稳定性计算
(1)结构面法向矢量
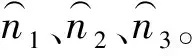
(2)块体移动方向
经过前文分析,裂隙块体仅可能发生平面剪切和楔型滑动破坏,即沿单平面或双平面发生滑动,且边坡无任何防护措施,块体将在重力作用下发生自由滑动。
若块体沿单面滑动,则有
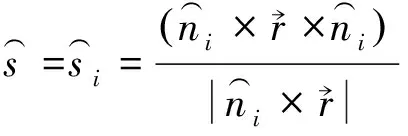
(10)
若块体沿双面滑动,则有
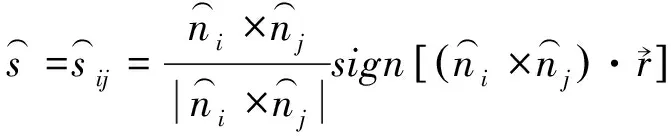
(11)
(3)可动块体的运动形式
①单面滑动
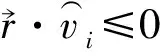
故满足的运动学条件可转化为
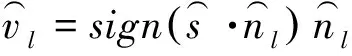
(12)
式中,l为可动块体的各结构面,且l≠i。
当块体沿P1结构面滑动时,有
可得沿P1结构面单面滑动的块体为U1∩L2∩L3。
同理得到,沿P2结构面单面滑动的块体为U1∩U2∩U3,沿P3结构面单面滑动的块体为L1∩L2∩U3。
②双面滑动
故满足的运动学条件可转化为
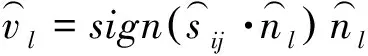
(13)
当块体沿P1、P2结构面滑动时,有
可得沿P1、P2双结构面滑动的块体为L1∩U2∩U3。
同理得到,沿P1、P3双结构面滑动的块体为U1∩L2∩U3,沿P2、P3双结构面滑动的块体为U1∩U2∩L3。
可以看出,高边坡可移动块体为JP000(U1∩U2∩U3)沿P2结构面单面滑动,与前文所述“岩体存在平面剪切型滑动破坏”结论相吻合。
(4)可动块体的稳定系数
由于结构面的黏聚力受几何形态、填充物、含水量等多因素控制变异性较大,且块体一旦滑动,其所贡献的抗滑力将大打折扣,故在可动块体的稳定性计算中,宜采用Barton模型确定的基本内摩擦角进行计算。
可移动块体为JP000(U1∩U2∩U3)沿P2结构面单面滑动,其稳定系数为
综上所述,高陡边坡上部松散堆积层滑动后,岩体应力重分布,稳定系数为1.04,基本上处于极限平衡状态,易发生平面剪切型滑动破坏,应加以防护。
5 结论
通过对宣绩高铁某高陡边坡现场调查,结合室内试验和Barton模型取值分析,通过极限平衡法、块体
理论等多种手段,对其稳定性进行了定性分析及定量计算,得到以下主要结论。
(1)通过对边坡地层结构的分析可知,上部残坡积土易沿土-岩接触面发生整体性圆弧型滑动破坏,受节理裂隙控制的关键岩体易发生平面剪切型、楔型滑动破坏。
(2)运用极限平衡法对土-岩接触面滑动破坏模式进行分析,可得边坡在天然工况下稳定系数为1.1,整体处于稳定状态,暴雨工况下稳定系数为1.046,处于极限平衡状态,在降雨作用下残坡积土易沿土岩接触面发生滑动。
(3)应用块体理论对边坡内部的重点块体进行研究,判断可移动块体为JP000(U1∩U2∩U3)沿P2结构面单面滑动,其稳定系数为1.04。
(4)鉴于土-岩混合边坡失稳形式的特殊性,分析时应针对不同的潜在破坏模式,采取多种方式综合评价,相互印证。
