复合MLINEX 对称损失下Pareto 分布参数的稳健Bayes 估计
2021-12-27周巧娟王慧丽
周巧娟,王慧丽
(1.南京审计大学金审学院 基础部,江苏 南京 210023;2.西安财经大学 统计学院,陕西 西安 710100)
0 引言
Pareto分布是一种重要的统计分布,是由意大利学者Pareto作为收入分布于1897年提出的,最初是用于分配理论中,后来被广泛地运用在很多领域,如:金融、保险、可靠性统计分析等,因此对此分布的研究具有重要的理论和应用价值. 目前,已有很多学者对Pareto分布的统计性质进行了研究. 王晓红在定时截尾数据下,研究了熵损失下Pareto分布参数的Bayes估计及可容许性[1];韩明在均方损失及熵损失下给出了Pareto分布形状参数的E-Bayes估计和多层Bayes估计,研究其可容许性[2];李秀敏等采用极大似然估计及其渐近正态性、轮廓似然估计和矩估计法对Pareto分布形状参数进行了估计[3];龙兵在双边定时截尾下对Pareto分布的参数进行了估计[4]. Ming Han在不同损失函数下研究了Pareto分布的E-Bayes估计,并引入期望均方误差来度量估计误差[5].
Podder.CK提出MLINEX函数以来[6],越来越多的学者关注MLINEX函数. 金秀岩在MLINEX损失函数的基础上,提出了复合MLINEX对称损失函数,并在该损失下得到了对数伽玛分布尺度参数的Bayes估计、E-Bayes估计和多层Bayes估计[7]. 朱宁等在尺度参数已知的情况下研究了复合MLINEX对称损失函数下Pareto分布参数的Bayes估计、E-Bayes估计以及多层Bayes估计,并证明其可容许性[8].
对于Bayes统计推断来说,参数估计的稳健性是一个重要的问题[9],上述各种损失下关于Pareto分布参数的讨论中均未涉及Bayes估计的稳健性的问题. 本文给出了复合MLINEX对称损失函数的一种特例,并在这种特殊的损失下研究了Pareto分布参数的一种稳健Bayes估计PRGM(Posterior regret gamma minimax)估计. 最后利用Monte Carlo方法对PRGM估计和极大似然估计进行了比较,说明了PRGM估计的优良性.
1 Pareto分布形状参数的极大似然估计
设随机变量X服从Pareto分布,且其分布函数及密度函数分别为
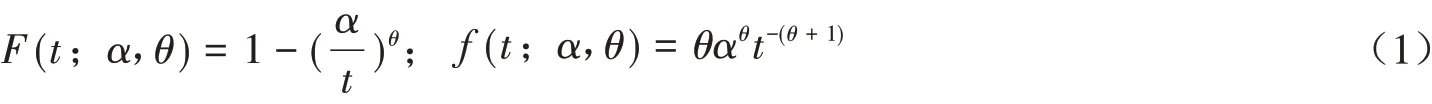
其中α是尺度参数,θ是形状参数,且0 <α≤t,θ> 0.
现有一批寿命服从Pareto分布的产品共有n个,进行定数截尾试验,直到有r个失效为止,记失效时刻为t1≤t2≤…≤tr,则(t1,…,tr)的联合分布密度为
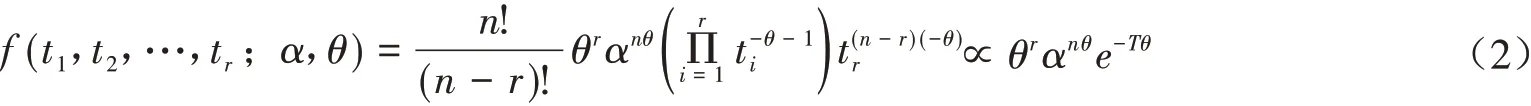
其中总的寿命试验时间

当(t1,…,tr)已知时,似然函数为,取对数得
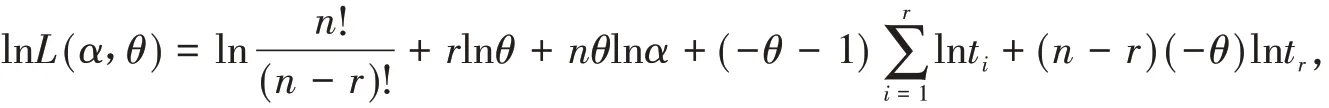

其中T如(3)式所示.
2 Pareto分布形状参数的PRGM估计
2.1 复合MLINEX 对称损失函数及其特例
MLINEX非对称损失函数的定义[10]:

复合MLINEX对称损失函数的定义[7]为:
其中δ为参数θ的估计.
为了利于求解参数的稳健Bayes估计,我们考虑如下特例:当ω= 1,c= 1时,损失函数为

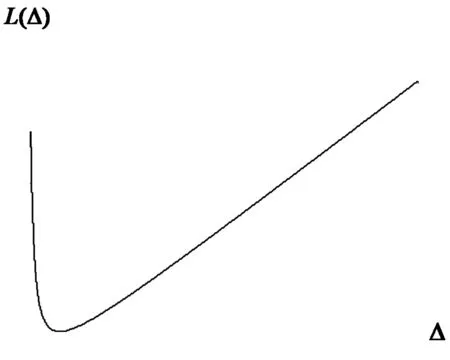
图1 损失函数(5)的图像
由图像可知该损失对Δ及δ均是向下凸的,相对于均衡损失而言,在损失函数(5)下过低估计比过高的估计有更重的惩罚.
2.2 α 已知时参数θ 的PRGM 估计
设Bayes统计推断中所采取的决策为δ=δ(x),损失函数为L(θ,δ(x)),x为子样,f(θ|x)为在子样x之下θ的后验概率密度,ρ(f(θ|x),δ)为采取决策δ的后验期望损失,则

假设α已知,那么当样本(t1,…,tr)已知时,T为常量,所以(2)式中参数仅为θ,取其共轭先验伽玛分布
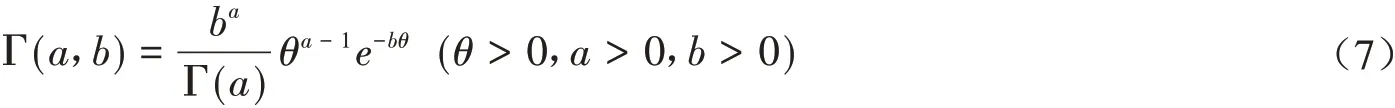
由(2)式和(7)式可得θ的后验密度函数为
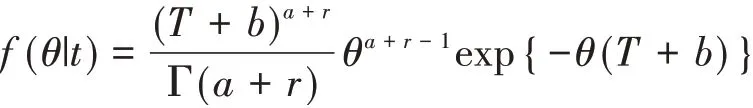
它仍为伽玛分布Ga(a+r,T+b).
那么,在损失函数(5)式的情况下,由(6)式可算得选取决策δ的后验期望损失为
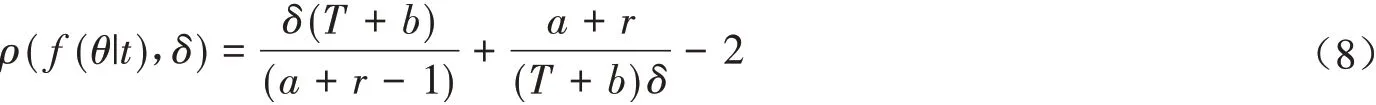
记δπ表示使后验期望损失达到最小的决策,即Bayes决策. 那么选取决策δ而不是δπ所构成的损失为定义1[9,11]如果有δ*∈D,满足


成立,则称δ*是θ的PRGM估计,记为δPRGM.
(i)令Γ1= {π(θ;a,b) = Γ(a,b),a=a0,b1≤b≤b2,θ> 0 },当π∈Γ1时,
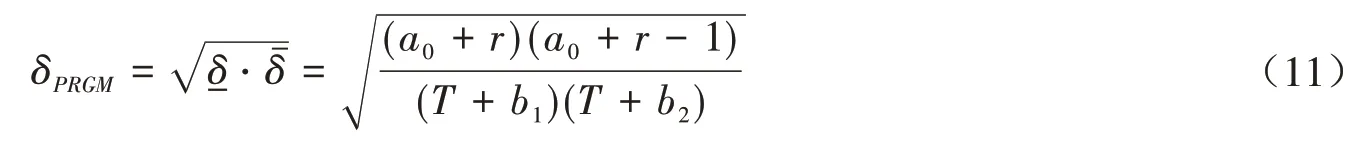
(ii)令Γ2= {π(θ;a,b) = Γ(a,b),b=b0,a1≤a≤a2,θ> 0 },当π∈Γ2时,
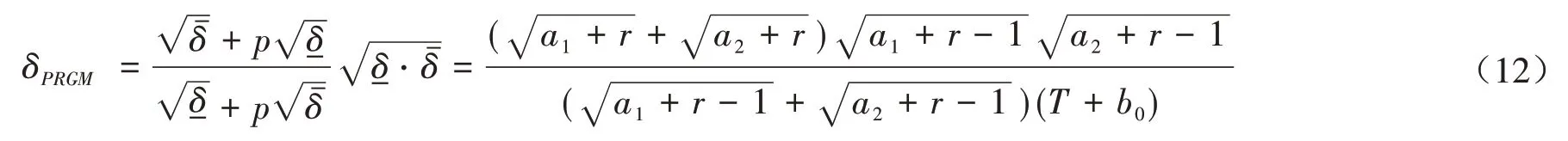
(iii)令Γ3= {π(θ;a,b) = Γ(a,b),a1≤a≤a2,b1≤b≤b2,θ> 0 },则当π∈Γ3时,
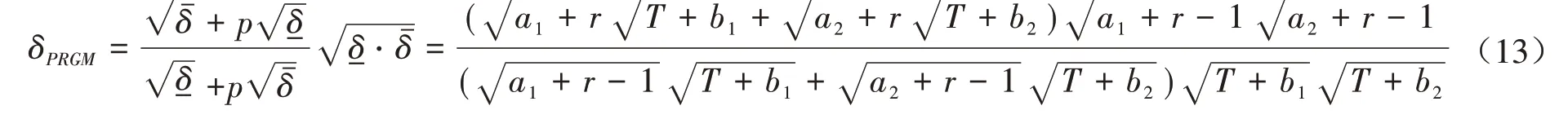
证明:(i)当π∈Γ1时,a=a0为常数,则由(9)式可知

对δπ求一阶、二阶偏导数得显然于是d(δ,δπ)对δπ是向下凸的函数,那么从以下三个方面寻找δ*,使δ*满足(10)式:
①当δ≤-δ时,
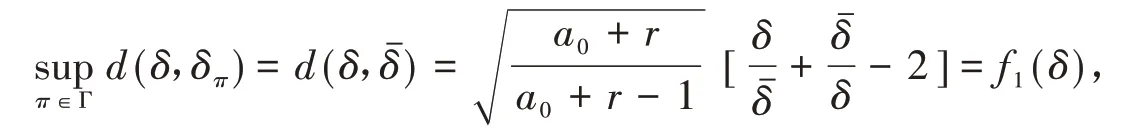
②当δ≥δˉ时,
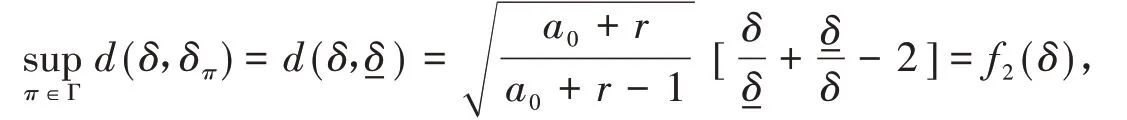
③当-δ<δ<时,
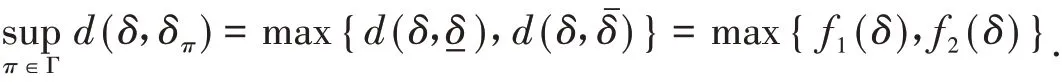

故g(δ)单调递减,且g(-δ) > 0,g() < 0,因此有且仅有一点δ*∈(-δ,)使g(δ*) = 0,即d(δ*,) =d(δ*,) .
当δ<δ*时,g(δ) > 0,即f1(δ) >f2(δ) 故,且f1(δ) 单调递减,因此δ*处达最小,即
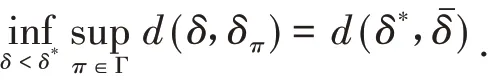
当δ>δ*时,g(δ) < 0,即f1(δ) 当π在Γ1中变化时,易得及,代入上式可得 (ii)当π∈Γ2时,由可知是a的函数,那么由可将d(δ,δπ)化为 其中B= 2(T+b0) > 0,d(δ,δπ)分别对δπ求一阶、二阶偏导数得 当π在Γ2中变化时,易得及,代入上式可得 由此解得δ*,即为δ的PRGM估计: 将-δ及δˉ,代入(14)式得 (iii)由(i)(ii)的讨论可知当超参数a或b变化时d(δ,δπ)对δπ均是向下凸的,因此当π∈Γ3时将及代入(14)式,即可得到结论. 关于PRGM估计稳健性评价,仍沿用参考文献[9]中运用的风险分析作为估计量的稳健性分析的基本方法. 若ρ(π,δ(x))表示决策δ(x)下的后验期望损失,那么决策δ(x)的稳健性指标为 由(15)式可知,若对任意取的值ε有 成立,则称该估计是ε稳健的. 因此,我们可以根据以上评价稳健性的指标来评价PRGM估计稳健性的好坏. 当Pareto分布中α已知时,取α= 5,待估参数θ的真值为0.5,n= 20,r= 15,通过Monte-Carlo方法产生服从U(0,1)的随机数U1,U2,…,U15,再由ti= 5 (1 -Ui)2产生15个服从Pareto分布的随机数t1~t15分别为:6.1825 6.6456 6.6809 10.2715 10.4686 11.3679 13.6512 15.4489 17.2681 17.3454 22.0955 25.4090 36.6815 42.3017 87.5335,那么经(3)式算得T= 32.0980. 取θ的先验分布族分别为: 分别在Γ1,Γ2,Γ3下,由计算公式(4)(11)(12)(13)(15)算得如下模拟结果: 表1 各分布族下α已知时θ的估计及损失(α = 5,θ = 0.5) 由上表可以看出,PRGM估计明显优于极大似然估计,且由后验稳健性可以看出,当先验分布π在分布族Γ1、Γ2及Γ3上变化时,PRGM估计的后验风险变化非常小,若取ε= 0.05,则PRGM估计都是ε稳健的,因此这种估计均具有较好的稳健性. 本文在复合MLINEX对称损失的一种特例下,给出了定数截尾模型下Pareto分布形状参数θ的一种稳健Bayes估计:PRGM估计,并通过Monte-Carlo方法对这种估计和极大似然估计进行了比较. 随机模拟结果表明PRGM估计明显优于极大似然估计且具有较好的稳健性.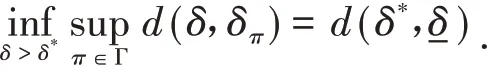




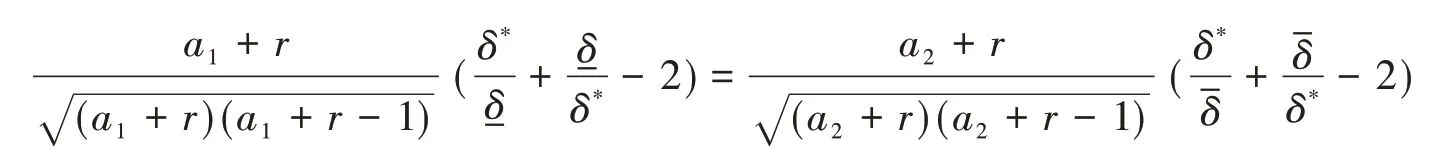

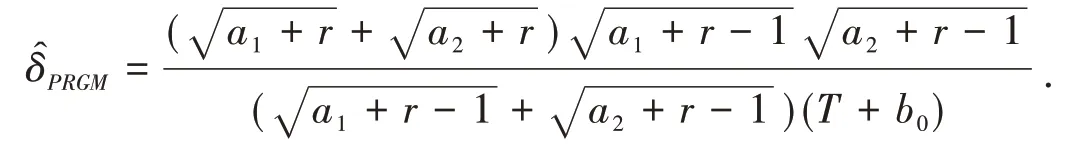
3 估计的稳健性评价
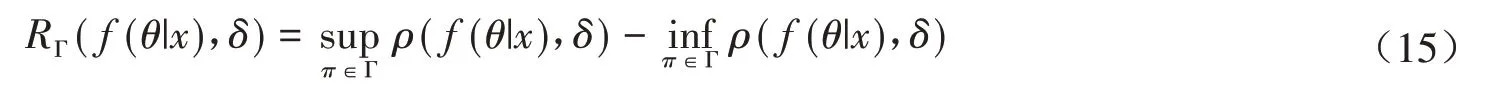
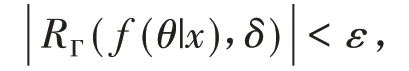
4 随机模拟例子
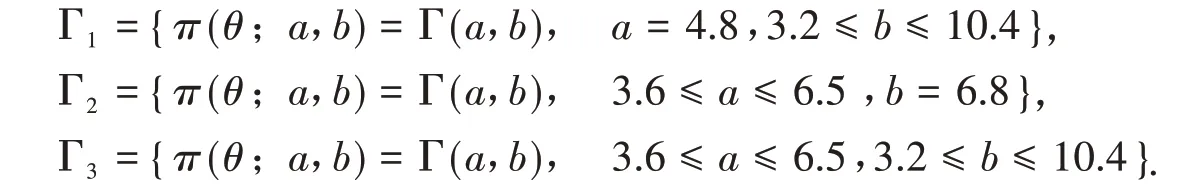

5 结束语
