考虑分布式储能功率四象限输出的主动配电网鲁棒优化调度模型

吴科成，高志华，刘瑞宽，高崇，张俊潇，梁咏秋，王凯亮

(1. 广东电网有限责任公司，广州510080；2. 广东电网有限责任公司电网规划研究中心，广州510080；3. 广东电网有限责任公司东莞供电局，广东 东莞523008)

0 引言

大量分布式电源接入可能会导致配电网出现电压波动、网络损耗增加等问题[1]，储能系统具有高能量密度和快速充放电能力，可为解决上述问题提供思路[2]。因此，研究应用储能系统提升配电网电压调整能力，提升配电网运行经济性具有重要意义。

近年来，学者们广泛研究了含储能系统的配电网优化调度问题。文献[3]提出了一种基于模型预测控制的主动配电网电压协调控制方法，其中储能系统作为一种参与电压调整的主动管理元素。文献[4]研究了如何利用用户侧储能系统解决含高比例光伏电源的配电网电压波动问题。文献[5]考虑了储能和柔性负荷的时空联系，以可再生能源利用率最大化、网损最小和用户满意度最高为目标函数构建了主动配电网多目标优化调度模型。文献[6]提出了一种改善配电网电压质量的分布式储能经济优化配置方法。文献[7]研究了应用储能系统平抑由于分布式电源接入引起的节点电压、负荷波动问题。建立了配电网中储能系统选址定容多目标优化模型，并采用改进的粒子群算法进行求解。文献[8]建立配电网风光储联合经济调度模型，对风电、光伏出力的随机性与储能充放电的有限时序性的协调配合问题进行了研究，并采用协同进化遗传算法的多种群进化机制对模型进行求解。文献[9]提出了考虑电压稳定的配电网分布式储能双层控制策略，上层稳定电压，确定各节点电压满足安全运行条件和电压偏差最小时储能群总的有功功率，下层对各储能系统进行功率分配。分布式储能系统包含电池储能(battery energy storage, BES)和功率转换装置功率转换系统(power conversion system, PCS)，以上研究中仅仅考虑了PCS的有功功率输出，而忽略了其无功功率输出能力[10]。

同时，大量具有随机特性的分布式电源会逐渐接入配电网中，其中风力发电是一种典型的可再生能源。因此，如何有效处理风电机组出力、负荷需求的不确定性成为了研究配电网优化调度问题的关键。针对此问题，学者们常采用随机规划和场景分析法对配电网中的不确定因素进行建模，模拟不确定性对配电网优化调度的影响。文献[11]建立了配电网风-光-储随机规划模型，采用ARMA模型对风-光的不确定性运行工况进行了场景抽取。文献[12]通过引入数据驱动的建模方法建立了主动配电网随机无功优化调度模型，基于第二阶段得到的最恶劣概率分布结果，第一阶段通过优化手段找到离散无功补偿设备的最优运行策略；第二阶段为寻找变量的不确定概率分布，用于校验第一阶段的结果。文献[13]研究了基于场景法的配电网有功-无功协调优化模型，主要考虑了风-光-荷的不确定性、风速与光照强度预测误差的相关性，采用拉丁超立方抽样法对风-光-荷的运行场景进行抽取。然而在上述研究中，无论是随机规划还是场景法都需要确定性的概率曲线生成场景，可能导致模型不能反映真实的运行情况。鲁棒优化通过不确定集对不确定变量进行描述，克服了随机规划方法和场景法中需要知道确切的概率分布的缺陷，通过优化手段得到“最恶劣”场景下的优化决策方案，更加符合实际的运行工况。

基于上述分析，为了解决大量分布式电源接入引起的配电网电压偏移和网损增加等问题，本文提出了一种考虑分布式储能功率四象限输出的配电网鲁棒优化调度模型，为利用分布式储能改善配电网电压调整能力、提高运行经济性等问题提供了思路。采用二阶锥松弛(second-order cone relaxation, SOC)技术对配电网最优潮流进行凸优化松弛，并采用Big-M法处理目标函数含绝对值的非线性项，将整个优化调度模型转换为一个混合整数规划问题。同时，应用区间鲁棒优化来表征配电网中风电出力和负荷需求不确定性。调用成熟的商业求解器CPLEX求解该模型。最后，在IEEE 33节点系统中仿真验证了应用分布式储能提升配电网电压调整能力、运行经济性的有效性。

1 整合分布式储能的配电网结构

传统配电网不存在反向潮流，主要负责从上级电网购电并可靠地供给终端用户。配电网管理系统(distribution management system, DMS)主要依靠SCADA系统从馈线终端和远控开关处收集有限的数据进行远程控制。随着配电网中大量分布式电源的，以及高级量测设备(advanced metering infrastructure, AMI)和信息通信技术(information and communication technologies, ICT)的发展，传统配电网正在向有源配电网发展。可以在配电网中布局不同种类的远程终端单元(remote terminal unit，RTU)收集各种运行数据(如运行状态信息)，控制主动管理对象(如分布式储能等)。因此，DMS可以通过收集信息，制定有效的日前调度计划，改善配电网的电压偏差等问题和实现整个系统的经济运行。图1为典型的含分布式储能系统的主动配电网结构，包括变电站RTU(substation RTU, SUB-RTU)、储能系统RTU(energy storage system RTU, ESS-RTU)、风电机组RTU(wind turbine generator RTU, WTG-RTU)和负荷RTU(load-RTU)。

图1 含分布式储能的配电网结构Fig.1 Structure of distribution network with distribute energy storage

DESS的接入配电网的电路图如图1所示，通过与功率转换系统(power conversion system, PCS)与配电网进行功率传输。电池储能BES释放或吸收电能，PCS为一个自换相的三相全桥逆变器[10]，通过控制电力电子器件的导通和开断，对输出电压大小和相位的改变，可以实现有功和无功功率的独立、快速调节，DESS控制器一般分为外环控制器和内环控制器[10]，具体的控制原理不是本文的研究重点，可以见文献[10]，此处不再赘述。DESS的功率四象限输出范围如图2所示。

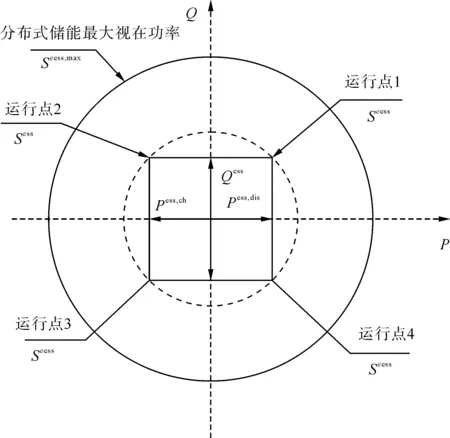
图2 分布式储能的运行原理图Fig.2 Operation schematic diagram of distributed energy storage

图2中Sess为储能的视在功率，Pch和Pdis分别为储能的充放电功率，Qess为储能的无功功率。当PCS外环控制器检测到配网需求有功功率和无功功率时，内环控制器控制DESS有功和无功功率输出大于0，电池处于放电状态，对外进行无功补偿，对应DESS工作模式处于第1象限；当外环控制器检测到配电网中有功和无功功率富余时，内环控制器控制有功、无功出力小于0，此时配电网向DESS输送有功和无功功率，电池处于充电状态，电容从外界吸收无功功率，对应DESS工作模式处于第3象限；同理，DESS也可工作于第2、4象限或是坐标轴上，根据实际需求灵活控制其充放电状态。具体DESS的详细运行约束见第2.2节。

2 分布式储能优化调度模型

在实际配电网运行过程中，DMS通过收集各种RTU的数据、电网电价信息、风电出力和负荷功率等信息，以最小化运行成本为目标，决策主动管理对象(本文主要研究分布式储能)未来24 h的调度计划。在运行过程中需满足支路潮流、网络安全、分布式储能安全运行等约束。在制定运行计划时需考虑风力出力和负荷需求的不确定性影响，本文采用区间鲁棒优化方法对风电出力和负荷功率的不确定性进行处理。

2.1 两阶段区间鲁棒优化数学模型

鲁棒优化模型是当前配电网日前优化决策中广泛应用的处理源-荷不确定性问题的方法。鲁棒优化决策模型能够保证配电网系统在给定的不确定性集合内安全运行。在两阶段鲁棒优化方法中，日前优化决策量被分为第一阶段决策变量和第二阶段决策变量。配电网的基本两阶段鲁棒优化决策模型可以表示为：

(1)

鲁棒优化模型的物理意义是寻找到最坏工况下的优化决策方案，以应对各种不确定场景，保证不确定集范围内任何取值，整个模型均可行。第一阶段变量{x}是包括配电网向上级电网购电量和购电状态的决策量。它们是在不确定参数实现之前确定的。第二阶段决策变量{y}被视为“wait-and-see”，可在风电出力和负荷需求场景改变之后进行灵活调整。第二阶段的决策变量包括可控负荷调整量、分布式储能系统的充放电行为等。

鲁棒优化的关键是如何应用不确定集刻画源-荷的不确定性，我们用ξ来分别表示配电网系统中风电机组出力和负荷用电的不确定性集，并采用以下盒式不确定集来刻画风电机组出力和负荷用电的不确定性。

(2)

(3)

以上两阶段鲁棒优化数学模型仅采用盒式不确定集对风电机组出力和负荷需求的不确定性进行了描述。当考虑光伏机组出力、冷热电负荷等其他因素的不确定性影响时，可采用类似的建模方式研究。

2.2 配电网鲁棒优化调度模型

2.2.1 目标函数

本文的配电网调度模型目标函数包含主网购电成本、网络损耗以及节点电压偏差惩罚费用，具体计算过程分别对应式(4)和式(5)。本文忽略了分布式储能等主动管理设备的运行维护成本。

(4)

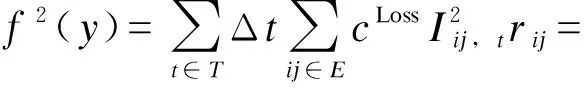
(5)

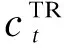
本文所提考虑电压偏差的配电网分布式储能优化调度模型包含以下几类约束：支路潮流约束、变电站约束、可控负荷运行约束、分布式储能运行约束以及线路、电压、风电机组限值约束。

2.2.2 配电网支路潮流约束

(6)

(7)

(8)

(9)

2.2.3 配电网络安全约束

(10)

(11)

2.2.4 变电站运行约束

(12)

2.2.5 可控负荷运行约束

(13)

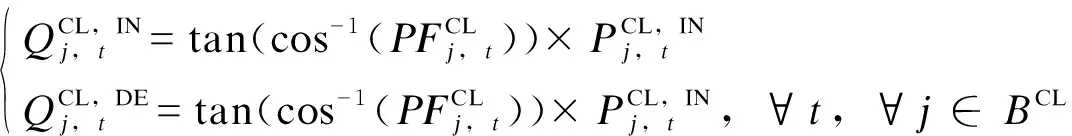
(14)

(15)

2.2.6 分布式储能运行约束

通常情况下，分布式储能系统需要考虑多时段的约束限制，包含充放电状态限制、充放电功率以及储能容量限制。

1)储能充放电状态限制

同一储能系统在某一运行时段不能同时充放电，通常通过引入0-1变量描述储能的充放电状态。

(16)

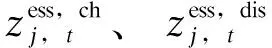
2)储能充放电功率限制

储能系统每个时段的充放电功率要受其自身的容量限制，考虑储能系统无功功率后的运行约束可表示如下[14]：

(17)

3)储能容量限制

储能系统各时段的容量都应保持在限制范围内。

(18)

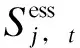
2.2.7 风电机组出力约束

(19)

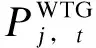
3 求解方法

本文第2节中构建的考虑分布式储能功率四象限输出的主动配电网优化调度模型中目标函数式(5)中包含绝对值，同时配电网支路潮流式(9)中也包含非线性项，导致优化调度模型为非凸非线性问题，难以求解，下面将对以上非线性项进行处理。同时采用CCG将主动配电网鲁棒优化调度模型分解为主问题和子问题进行迭代求解。

3.1 调度模型线性化转换

3.1.1 目标函数的线性化转换

首先对于目标函数中的绝对值项，通过引入0-1辅助变量μj,t去掉绝对值符号。

|Vj,t-1|=(2μj,t-1)(Vj,t-1)

(20)

当μj,t=1，(Vj,t-1)为非负；当μj,t=0，(Vj,t-1)为负。上述关系可采用Big-M法线性表达为：

(21)

式中：ψj,t为连续型辅助变量，用于替代μj,t(Vj,t-1)， 当μj,t=0时，式(21)约束下ψj,t也为0，(Vj,t-1)为非负；当μj,t=1时，式(21)约束下ψj,t=(Vj,t-1)， 为非负值；其中M为一个恒大于(Vj,t-1)的常数。

3.1.2 运行约束凸松弛

原配电网支路最优潮流模型为非线性规划模型，对原平方项进行替换，如式(22)所示。

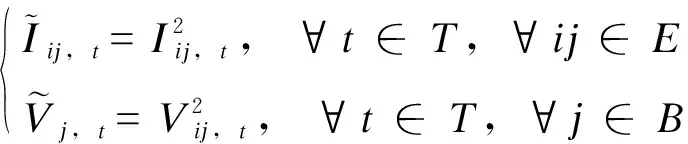
(22)

对式(9)进行二阶锥松弛转化[15]，得到如下基于支路潮流模型的松弛最优潮流。

(23)

通过对目标函数和约束条件进行线性化转化后，第2节中建立的主动配电网优化调度模型便转化为一个混合整数二阶锥规划问题，可以直接采用成熟的商业求解软件进行求解。

3.2 基于CCG算法的两阶段鲁棒优化求解

为了方便后面的描述，下面采用矩阵形式描述前面构建的配电网优化调度模型。

(24)

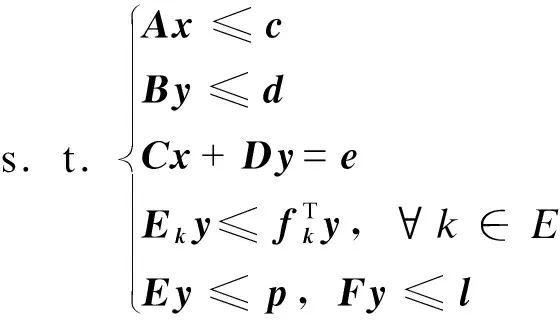
(25)

本文所提出的配电网两阶段鲁棒优化调度模型为三层min-max-min问题，需将原文题分解为主问题(master problem, MP)和子问题(sub-problem, SP)进行迭代求解。由于CCG算法相比其他算法具有更好的收敛性[15]，本文采用CCG算法对配电网的优化调度模型进行求解。

3.2.1 CCG算法主问题

(26)

(27)

第s次迭代后，子问题寻找到了新的worst-case场景并添加到主问题中，主问题求得最优解(x*,δ,ys)， 此时主问题为原模型提供了1个下界值。

3.2.2 CCG算法子问题

根据主问题得到的第一阶段变量决策结果{x*}， 子问题对内层max-min模型进行优化求解，子问题实质上是重新寻找使目标值更大的不确定性恶劣场景，其为原模型提供了1个上界值。

(28)

(29)

子问题式(28)双层max-min规划模型可通过对偶原理求解转换为如下单层max优化决策模型。

(30)

(31)

式中：χ1、χ2、χ3、χ4、χ5、χ6分别对应模型式(29)中决策变量{y}的对偶变量。可以看出，式(28)中max-min形式通过对偶转化为模型(30)中的max形式后，目标函数中包含非线性项lTχ5和pTχ6， max决策模型为非凸规划问题。

本文采用盒式不确定集来表征光伏出力和负荷功率的不确定性，由文献[16]知max模型最优解在极值点处获得，这些不确定集可以用二进制变量和一系列线性约束表述并对上述双线性项进行转换，从而可以快速求解。

3.2.3 鲁棒优化调度模型求解流程

综上所述，配电网两阶段鲁棒优化调度模型的具体求解步骤如下。

步骤1：初始化：设定下界值LB=1×10-8和上界值UB=1×108，设置迭代次数s=1和算法迭代收敛条件ε；

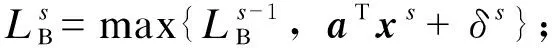
步骤5：更新s=s+1，然后转到步骤2。

4 算例分析

我们采用IEEE 33节点电网系统[16]验证本文所提模型和求解方法的有效性。本章所有程序在MATLAB R2016a环境下基于CPLEX12.6.0算法包进行计算，个人电脑硬件环境为Intel(R) Core(TM) i7- 10710U CPU @1.1 GHz 1.61 GHz，16 GB内存，操作系统为Windows 10 64 bit。

4.1 算例参数配置

测试系统的网络参数见文献[16]，主要在系统中配置两种类型的储能系统，其详细参数如表1所示。同时系统内某些节点的负荷为可控负荷，可控负荷的详细参数见表2。为了对比分布式储能的不同配置方式对配电网电压偏差和网络损耗的影响，设置不同的验证场景，不同场景的系统配置信息见表3，其中括号内表示配置的类型，括号外数字表示安装节点位置。系统总有功负荷需求和风电出力曲线见图3。主网购电价格见图4。主网出力上下限为5 MW和0.5 MW。额定电压为12.66 kV，节点电压范围为[0.94, 1.06] p.u.。支路电流上限为400 A。

表1 分布式储能参数Tab.1 Parameters of energy storage system

表2 可控负荷参数Tab.2 Parameters of controllable load

表3 不同场景下系统配置Tab.3 System configuration for some new elements in different cases

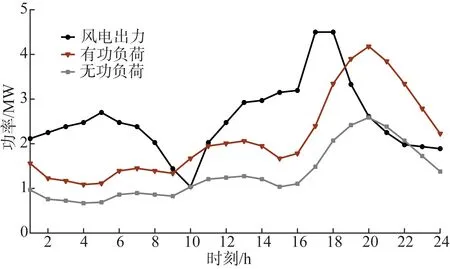
图3 有功无功负荷需求和风电机组出力Fig.3 Total active/reactive load demand and total wind power output

图4 主网购电价格Fig.4 Electricity purchasing price of main-grid

4.2 储能不同配置方式的影响分析

为了对比分析分布式储能参与电压调整的有效性，本文根据储能的不同配置方式设置了4种算例场景。

Case1: 系统未配置储能系统；

Case2: 系统某一节点配置一个容量较大的储能系统(容量为2 MW)；

Case3: 配置总容量大小相同、分布相对分散的小容量储能系统(单个容量为0.4 MW)；

Case4: 系统配置储能系统的节点和位置和Case3相同，同时考虑储能系统的功率四象限输出。

本小节分析中，风电和负荷的波动范围刻画系数αW和αL都取0.05。图5为Case2—Case4中储能系统的充放电功率。负荷高峰时期为减少从主网的购电量以及满足高峰负荷需求，储能处于放电状态。

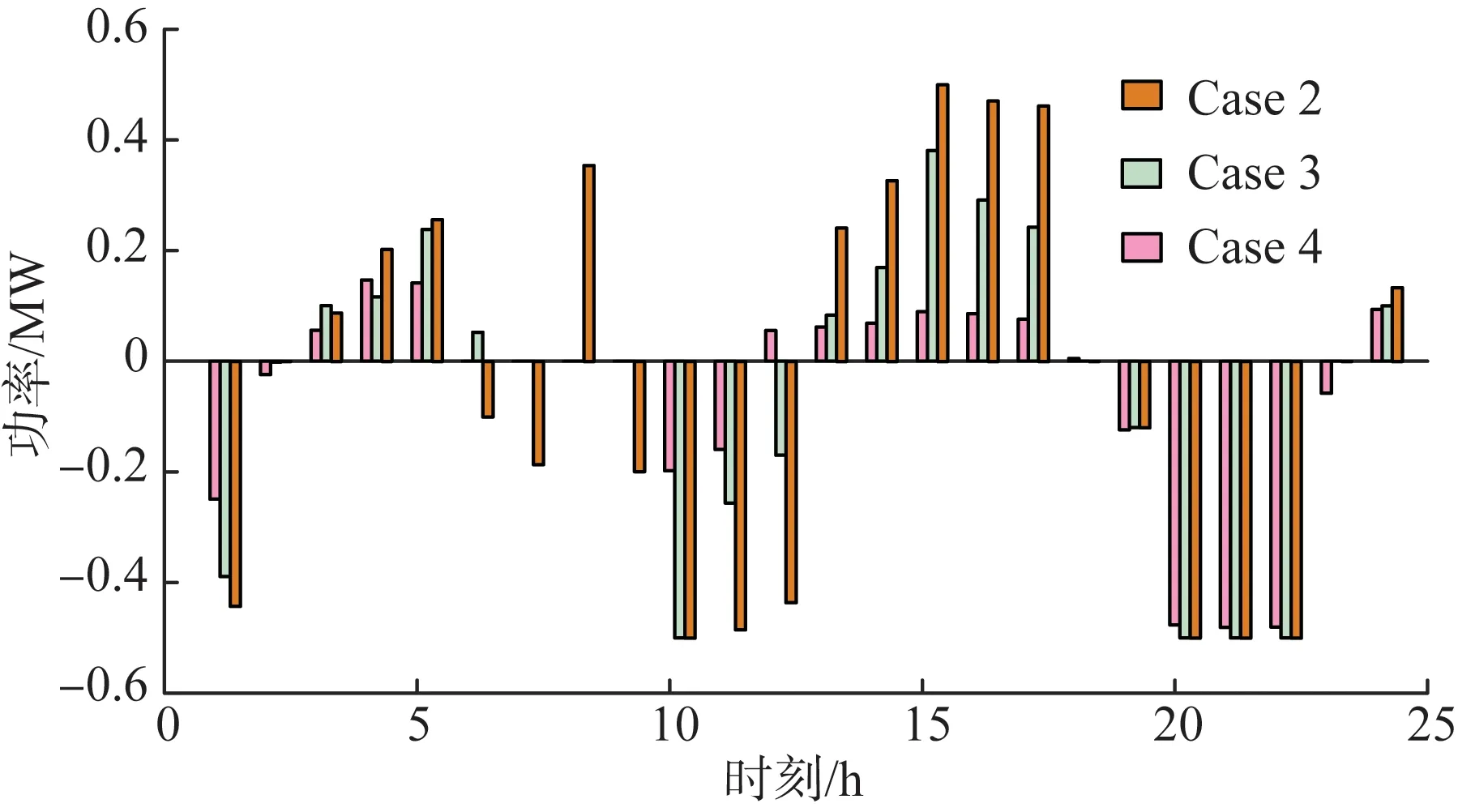
图5 不同场景下的储能充放电功率Fig.5 Charge/discharge power of energy storage system in different cases

为了清晰展示储能系统参与配电网电压调整的有效性，选取不同场景下典型时段(t=12)各节点的电压进行对比分析，对比结果图如图6所示。

图6 不同场景下t=12时各节点电压值Fig.6 Node voltage value in different cases when t=12

在Case1和Case2中，大部分节点的电压明显偏离基准值，节点25、28、29、30的电压值甚至接近0.97 p.u.。而在Case3中各节点的电压值偏移幅度相对减小，在制定配电网的运行时，考虑了分布式储能系统的功率四象限输出时(Case4)，各节点的电压值基本保持在0.99～1.00 p.u.之间，各节点电压偏差很小。可以看出分布式储能可有效提升系统的调压能力，减少各节点的电压偏差。分布式储能系统进行无功出力可同时提升系统的调压能力，将电压偏差惩罚费用由1 024.9 美元降低为775.8 美元。

为了更加全面的展示分布式储能对系统的电压调节效果，图7和图8给出了Case3和Case4场景下各运行时段各节点的电压分布结果，总体来看，Case4中电压偏差比Case3中各时段各节点的电压偏差要小。结果表明，若允许储能系统进行无功出力，则系统的调压能力将显著提升。

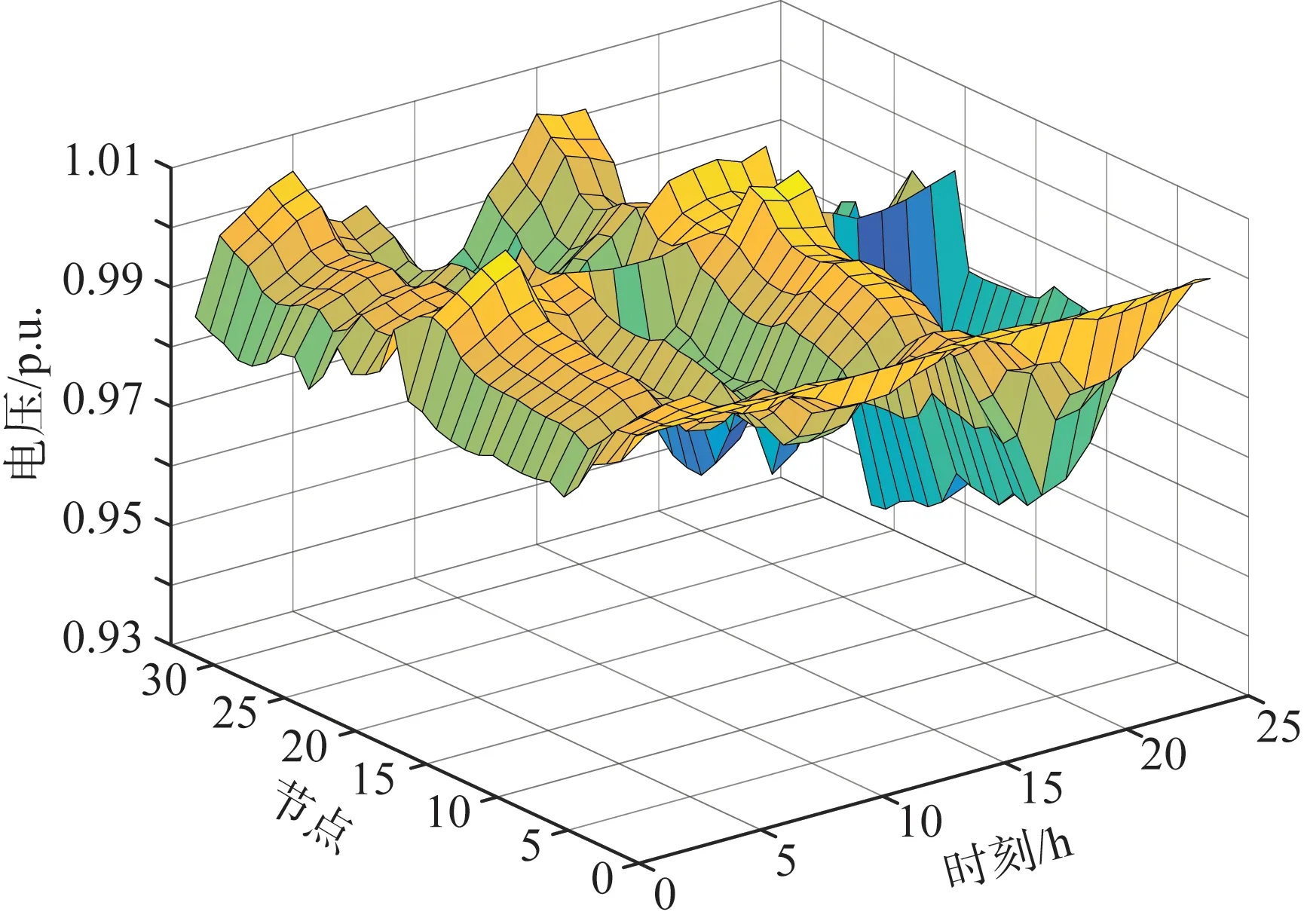
图7 Case3中电压分布图Fig.7 Voltage distribution in Case3

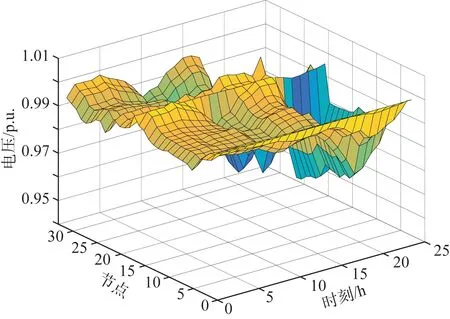
图8 Case4中电压分布图Fig.8 Voltage distribution in Case4

表4对上述4个场景下的电压调节综合效果及其经济性进行了详细阐述。

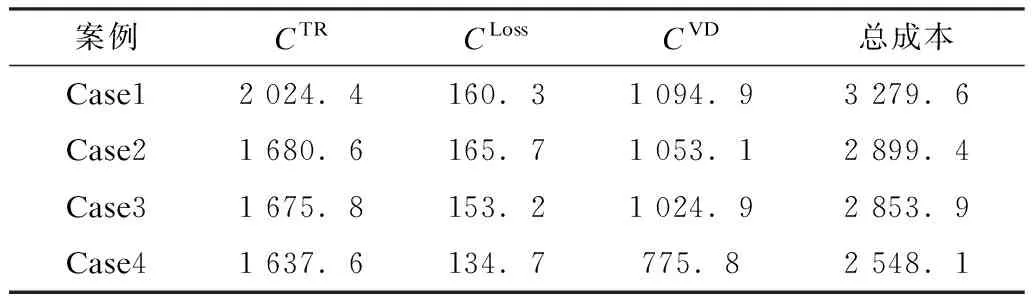
表4 不同场景下的运行成本Tab.4 Operation cost in different cases美元

Case1—Case4中系统的总运行成本分别为3 279.6美元、2 899.4美元、2 853.9美元和2 548.1美元。相比于Case1，Case2、Case3和Case4中系统的总运行成本分别减少了11.6%，12.9%，22.3%。可以看出，安装储能装置可以明显减低系统的运行成本，而分散储能的配置方式对降低系统的运行成本效果更佳。其中主要原因是减少了各节点的电压偏差，减小了系统损耗。若允许储能系统进行无功出力，可显著提升配电网系统运行的经济性。

4.3 鲁棒优化与确定性方法对比分析

配电网系统中风电机组出力和负荷功率的波动会对含分布式储能的配电网调度运行结果产生影响，文中第2.1节给定了不确定集来描述风电出力和负荷功率的波动，其中αW和αL为波动范围的刻画系数。下面我们通过对比不同波动范围下配电网在鲁棒优化模型下和确定性优化方法下的运行结果进一步分析鲁棒优化方法在处理配电网系统中不确定性的优势。采用蒙特卡洛(Monte Carlo simulation, MCS)随机模拟生成100 000个场景，并筛选出导致运行成本最大的恶劣场景。表5为不同波动范围下配电网的运行成本，可以看出随着αW的增大，鲁棒优化方法和确定性优化方法下最恶劣场景的运行成本都随着增加。

表5 不同波动范围下的最恶劣场景运行成本Tab.5 The worst-case operation cost under different αW

为了清晰展示鲁棒优化方法下和确定性优化方法下配电网调度运行结果，我们定义如下配电网总运行成本相对差指标：

(32)

式中：CRO为鲁棒优化方法下配电网的运行成本；CDA为配电网最恶劣场景下确定性优化运行成本；光伏出力和负荷功率不同波动范围下区域多微电网的总运行成本相对差结果如图9所示。

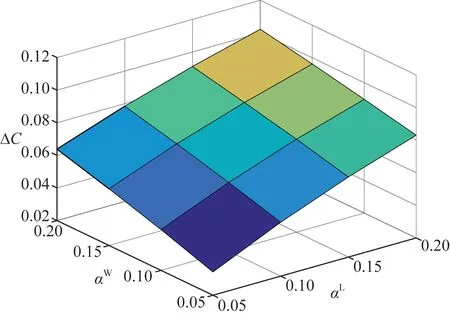
图9 不同波动范围下总成本相对差Fig.9 ΔC under different charge/discharge power of DESS

从图中可以看出，随着波动范围系数αW和αL的增大，鲁棒优化模型和确定性优化模型下配电网总运行成本相对差在增大，显然，鲁棒优化方法更具经济性。并且随着波动范围增大，鲁棒优化方法更能抵抗配电网系统中的不确定性，鲁棒优化决策模型在最恶劣工况下的表现更佳。因此，DMS在决策运行交易计划时有必要利用鲁棒优化模型处理系统内部的源-荷不确定性，特别当风电出力和负荷功率波动较大时。

4.4 配电网二阶锥松弛准确性分析

为了验证基于支路潮流模型的松弛最优潮流的准确性，下面定义二阶锥松弛相对误差指标。

(33)

图10为各运行时段的误差散点图。显然，松弛后的偏差结果满足运行要求，为10-4量级。结果表明，采用二阶锥松弛技术处理配电网交流最优潮流是有效的。

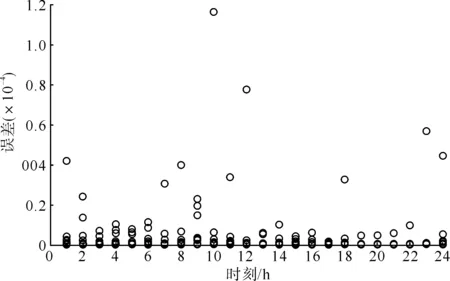
图10 各时段的误差散点图Fig.10 Error scatters under different periods

5 结论

本文提出了考虑分布式储能功率四象限输出的配电网优化调度方法，并应用盒式不确定集来表征风电出力和负荷功率的不确定性。在分析分布式储能功率四象限输出原理的基础上，通过引入0-1变量和对配电网交流潮流进行松弛处理，解决了潮流双向流动的电力网络中难以考虑电压的问题。并在IEEE 33节点系统中验证了本文所提模型的有效性，具体结论总结如下。

1)通过采用Big-M方法对目标函数中含有绝对值项进行处理和配电网交流潮流含有非线性项进行二阶锥松弛处理，从而将原分布式储能优化调度模型转换为混合整数二阶锥规划问题，可以采用成熟商业软件进行快速求解。

2)相比于集中式储能，储能分布式配置的方式更有利于改善系统的电压质量。若允许分布式储能进行无功出力，则系统的调压能力将显著提升，降低了系统的网络损耗，减少了配电网的电能损失。

3)应用区间鲁棒优化来表征配电网中的风电出力和负荷需求不确定性，从而对分布式储能、可控负荷、变电站等的日前运行计划进行决策，制定出鲁棒调度方案。算例仿真研究表明区间鲁棒优化调度模型相比于确定性方法在恶劣工况下表现更佳。

综合能源系统的协调优化运行是未来发展的趋势，如何有效考虑冷热电负荷的不确定性影响是下一步需要重点研究问题。