GreenLab模型20余年研究回顾与展望

康孟珍 王秀娟 华 净 胡包钢 王飞跃 De Reffye Philippe

（1.中国科学院自动化研究所复杂系统管理与控制国家重点实验室，北京 100190；2.中国科学院大学人工智能学院，北京 100049；3.北京市智能化技术与系统工程技术研究中心，北京 100190；4.中国科学院自动化研究所模式识别国家重点实验室，北京 100190；5.法国农业发展研究中心，植物学与植物构造模型联合实验室，蒙彼利埃 F-34398）

1 引言

20世纪90年代起，随着计算机技术的迅猛发展，为了更好地表达作物内在的生长发育规律及在不同环境条件下的植物可塑性，模拟植物的生长和发育这两个基本过程的植物功能结构模型（Functional-Structural Plant Model,FSPM）[1]应运而生。在过去的20 多年间，产生了ALMIS[2]，LIGNUM[3]，L-Peach[4]等多种FSPM，以及一些开放模拟平台，如OpenAlea[5]，GroIMP[6]等。作为FSPM中的一员，GreenLab模型起源于法国AMAP 模型，后者可追溯到20 世纪70 年代对咖啡树的模拟[7]。之后成功用于植物形态的构建[8]，并形成了包含数百种植物的商用虚拟植物库。与着重于计算机图形学的其他虚拟植物库如Speedtree和OnyxTree等相比，AMAP植物库的特色是基于植物学家对植物结构的分类即构造模型（Architectural Model）[9]而设计，使得虚拟植物的发育过程忠于植物学原理[8]。这一特点为模型在农学中的应用奠定了基础。

由于对生长过程模型的需求，AMAP模型在结构模拟基础上引入了对植物物质产生和分配过程的模拟，提出了以水作为生长驱动因子的AMAPHydro[10]。1998 年起，随着中法联合实验室成立，在AMAP 系列模型基础上发展了器官尺度的GreenLab功能结构模型，建模对象涵盖从草本作物到复杂树木的几十种植物类型。历经20 多年发表了200 多篇论文，联合培养了数十名研究生。本文总结GreenLab模型的基本概念、主要理论及特色内容，并对Green-Lab模型的未来发展进行展望。

2 GreenLab模型概述

GreenLab 模型与基于过程的作物模型类似，采用离散动态系统的形式来描述植物的生长和发育过程[11]，如式（1）：

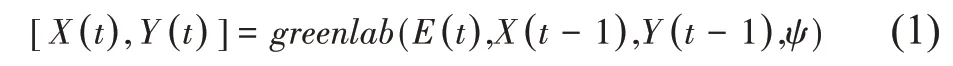
其中，ψ为模型参数集；t为生长年龄；X(t)为描述植物结构的变量，包括各种器官（叶子、节间、果等）的数量，由发育子模型计算；Y(t)为描述植物生长的变量，包括产生的生物量、器官总重以及单个器官重等，由生长子模型计算；E(t)为环境因子，包括各个周期的光强、温度、CO2浓度等。其中，发育子模型与生长子模型相互作用：前者为后者提供参与光合和物质分配的各类器官的数量，而后者为前者提供器官大小，从而可计算植物的三维形态。

GreenLab模型具有如下特点：

（一）模型具有通用性，涵盖的植物类型包括草本作物和复杂的树木。原因在于：（1）其中的发育模型涵盖了植物学家提炼出的各种构造模型，（2）其中的生长模型采用了作物生长和发育的基本生态生理机理和假设，例如积温（Thermal time）、资源利用效率（Resource use efficiency）、公共生物量池（Common biomass pool）等。最终得以通过一组数量相对较少的参数描述植物的生长和发育过程。

（二）模型求参方法具有通用性。对于不同类型的植物，不论是确定性还是随机性生长的植物，均可基于通用的拟合数据进行模型参数的逆向估计。由于部分模型参数难以直接测量（如器官库强参数），尤其是对于随机生长的植物，需要解决如何对植物的结构进行采样从而获取拟合数据的问题。在面向不同植物应用的过程中，形成了一套可以面向不同类型植物的拟合目标数据标准和参数反求方法。

（三）理论计算与模拟软件并重。对于随机模型，固然可以通过蒙特卡洛方法模拟不同的随机植物个体，但更重要的且非常具有挑战性的是模型统计量的理论计算，例如平均意义上的植物结构、平均生物量、平均器官大小等。GreenLab 模型统计量的理论计算一方面用于检查模拟软件正确与否，一方面用于参数逆向估计时的迭代计算。

此外，GreenLab 模型还提出了颇具特色的树木年轮生长子模型[12]，以及草本植物花序生长子模型[13,14]。子模型的选择往往取决于模拟对象是否具有代表性，涵盖了一类植物的共性特征。

3 结构模型

结构模型（Structural model），或发育模型（Development model），指基于植物学，采用计算机语言对植物结构进行抽象表达，动态地模拟植物的结构形成和器官发生过程的模型。

3.1 基本概念

GreenLab 模型沿用了AMAP 模型中的植物学概念，包括叶元（Phytomer）、生长单元（Growth unit）、生长轴（Bearing axis）和分枝系统（Branching system）等[15]。

叶元包括一个节间、节以及附生的器官（叶子、果和腋生分生组织等）[16]。

生长单元由连续的叶元产生，常见于树木。

生长轴由连续生长的叶元（作物）或生长单元（树木）形成。

分枝系统由生长轴及其附着的分枝构成。

植物学家Francis Hallé 等对自然界的植物的结构和发育类型进行了定性描述，从而归纳出了23 种构造模型[9]，每种构造模型代表着一类植物的发育特点。因此，通过对这23 种构造模型进行模拟，可以测试所提出的结构模型的通用性。

基于上述归纳的23 种构造模型，GreenLab 模型提出了生理年龄（Physiological Age,PA）和生长年龄（Chronological Age,CA）的概念，可以对植物结构和发育进行空间和时间离散化。

生理年龄用于表征不同的分枝类别。例如咖啡树中，主茎直立生长，而分枝斜向生长。模型用整数(p=1,…,maxp)表示生理年龄：主茎的生理年龄为1，分枝的生理年龄可能与主茎相同（重复生长的情况，可产生分形结构），或者大于主茎（普通分枝的情况）。一般植物的最大生理年龄maxp不超过5。对于作物，生理年龄一般与分枝级别对应：一级分枝的生理年龄为2，二级分枝的为3。对于树木，附着于同一生长单元的同一级别的分枝可对应不同的生理年龄，例如生长旺盛的长枝具有较小生理年龄，而短小的果枝则具有较大的生理年龄。

生长年龄用于表征植物或器官产生以来的发育周期，对应于离散化的时间。模型中，植物主茎末端产生一个新叶元所需的平均持续时间（积温）称为发育周期（Development Cycle，DC），以度日(Degree day)表示。对于节律性生长的树木，还存在另一种对应于生长单元的时间周期，称为生长周期(Growth Cycle,GC)[17]，可以由多个DC 构成。植物的生长年龄用发育周期t表示。基于发育周期划分的生长年龄建立了植物的发育和生长之间的时空联系，便于在同一时间尺度下模拟植物的器官建成和器官扩展。

3.2 双尺度自动机发育模型

GreenLab采用双尺度自动机（Dual-scale automaton）[16]模拟植物的发育过程，其中不同状态跳转关系可以通过图直观表示[18]。如图1 所示，每个微状态（Micro-state）对应于叶元，多个微状态跳转形成宏状态（Macro-state），对应于生长单元。多个宏状态的跳转即可模拟生长轴的发育，不同状态的跳转用箭头表示。侧芽的生理年龄用不同的颜色区分。随着轴的发育，侧芽同步发育，形成分枝系统。由于侧枝的生理年龄大于或等于母枝，因此参数可以用上三角矩阵形式表示，设置生长单元中叶元的种类、个数、侧枝的生理年龄和个数等[19]。该自动机与植物结构模拟领域的另一种常用方法L系统可以相互转换，不同之处在于L系统需要基于观察对象写出字符串替换规则，而自动机的重点在于如何区分分枝的类别和数量，据此设置自动机参数。自动机的结构可以是单尺度或双尺度，取决于分生组织为连续性或节律性的发育，前者主要面向作物，后者主要是面向以年为周期产生一个或多个生长单元的树木。

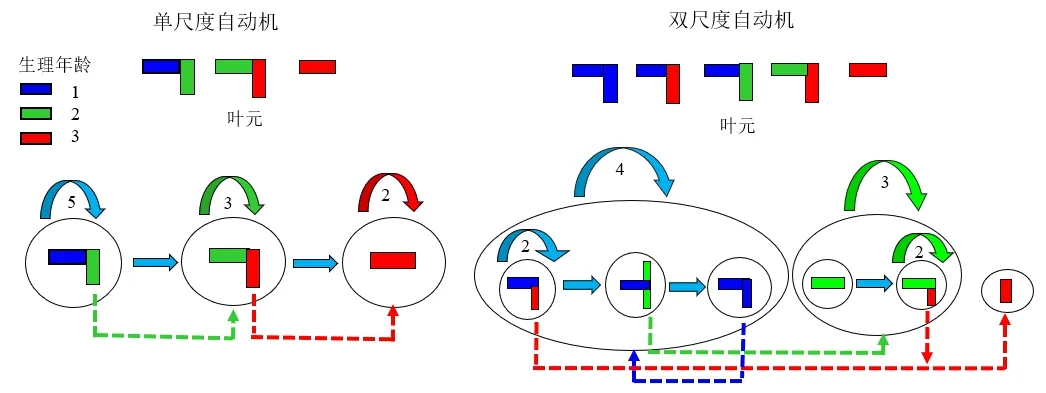
图1 基于自动机的植物发育模型Fig.1 Plant development model based on automaton

3.3 植物发育中的随机性模拟

大多数植物的发育受到影响分生组织活动的复杂因素的影响，导致植物个体结构之间存在差异，例如小麦植株的分蘖个数以及分蘖中的叶元数各不相同。为描述这些现象，GreenLab 在自动机中引入了影响发育的主要事件的概率，包括分生组织的发育概率（Development probability）、存活概率（Ⅴiability probability）和分枝概率（Branching probability）[17]。这些概率值可随时间变化。

发育概率bp用于描述在相同时间内同类生长轴产生的生长单元个数不同的现象，表示生理年龄为p的生长轴在每个生长周期的生长单元实际产生的概率。t个生长周期内产生的生长单元数服从二项分布B(t,bp)。

存活概率cp用于描述由于营养、病虫害等原因，生长轴顶端分生组织停止活动即死亡的现象，表示生理年龄为p的生长轴在每个生长周期能够继续产生生长单元的概率。分生组织存活的时间服从几何分布G(cp)。存活概率对植物结构的影响较为明显。

分枝概率ap用于描述腋生分生组织（芽）有的产生分枝，有的休眠的现象，表示生理年龄为p的芽能够发育成子结构的概率。

3.4 潜在结构

由于各种概率的存在，使得每个生长单元具有一个存在（发生）概率，由三种概率之积计算得到，表示该生长单元实际产生的数学期望，可以与模拟的结果进行比较，从而验证模拟结果的正确性。如通过颜色梯度表示潜在结构，可看出生长单元的存在概率随着植物的发育逐渐降低。

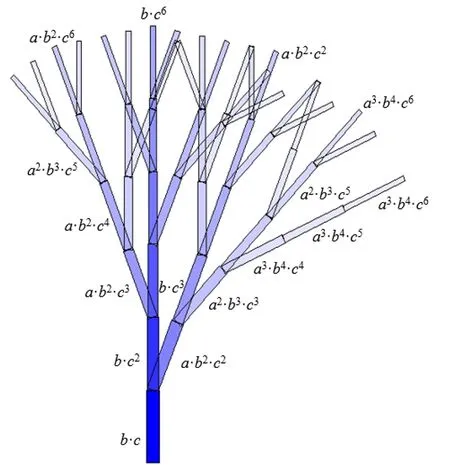
图2 随机发育情况下的潜在结构Fig.2 Potential structures in the case of stochastic development

3.5 植物器官数量的计算

根据生理年龄及其跳转关系，GreenLab 模型可以递归地用子结构（sub-structure）算法计算给定的周期内产生的叶元的数量，而无需逐个遍历[20]。基于结构分解，可以通过矩阵运算快速地计算和模拟植物的结构，包括随机结构[21]。此特征对于包含大量器官的树木模型非常重要。下文以双尺度自动机为例进行计算方式的说明，单尺度的情况在此基础上简化。

首先约定模型参数的命名：

np,q:生理年龄为p的叶元上包含的生理年龄为q的侧芽个数（p≤q）。

Np:生理年龄为p的生长轴中包含的最大生长单元数。

Jp:生理年龄为p的生长轴达到最大生长单元数后新的生长单元的生理年龄。

其次约定子结构中叶元个数的变量名：

Sp(t):在生长年龄t时出现的、生理年龄为p的子结构（分枝系统）中包含的叶元个数。

在生长年龄t时出现的、生理年龄为p的子结构（分枝系统）中包含的器官o的个数。

Up(t):在生长年龄t时出现的、生理年龄为p的子结构的生长轴中包含的叶元个数。

在生长年龄t时出现的、生理年龄为p的子结构的生长轴中包含的器官o的个数。

由于生理年龄为p的子结构中包含生理年龄不小于p的叶元，因此，Sp(t)可以表示为包含maxp的元素的行矩阵，每个元素为sp,q(t)(q=1,2,…,maxp)，表示其中所包含的生理年龄为q的叶元的个数。对于q＜p的情况，sp,q(t)=0。同理将Up(t)表示为行矩阵，其中仅第p个为非零元素。基于结构分解的计算公式如下。

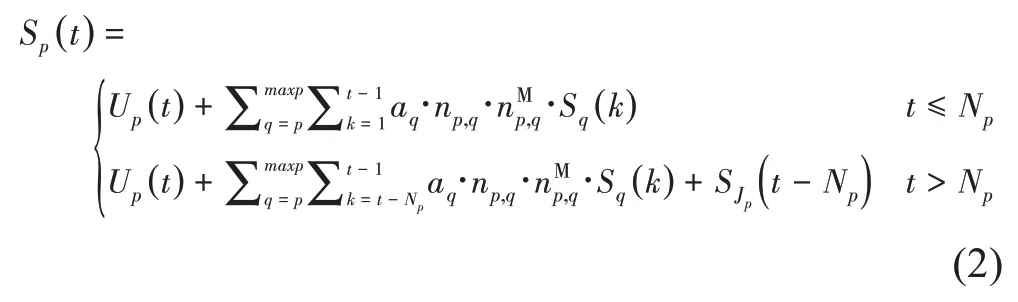
其中，在生长年龄t出现的、生理年龄为p的子结构的生长轴中包含的叶元个数为：

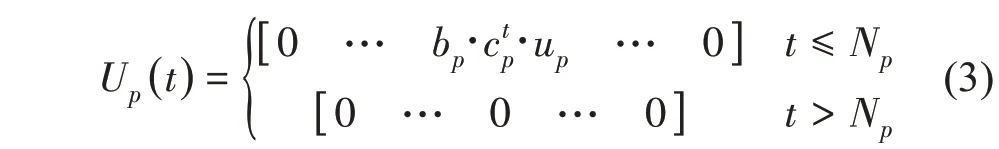
如将上述公式中的up换成则得到了各个周期产生的器官数量。生理年龄为1 的结构即植株本身：为了简化，下文记为对于面向作物的单尺度自动机的情况，则up=1。对于一年多次抽条发育的树木，如中杨树、枫树，则up本身就是一个随机变量，其期望另行计算。以杨树为例，单个生长单元内的叶元个数包含两部分：预先完成发育（preformation）直接扩展的叶元，以及在生长单元中新形成的（neoformation）叶元，需分别定义对应概率进行描述，限于篇幅不详述。

4 功能模型

功能模型（Functional model），或生长模型（Growth model），用于计算生物量的产生及其在植物内各器官间的分配，以及器官的大小。GreenLab 模型基于叶面积计算生物量的生产，并按生长周期进行迭代计算。模型框架与基于过程的作物模型（Process-Based Model）例如TomSim[22]具有共性，共用一些模型概念。差别主要在于模型的时空尺度和细节。

4.1 基本概念

与基于过程的作物模型相同，GreenLab 也使用公共生物量池的假设[23]，即认为光合作用产生的生物量存储在公共池中，并分配到各类器官。这个假设隐含了物质传输与路径无关的假设，这对建模是非常重要的简化。生长模型的初始生物量来源于种子，而后由叶子作为源器官提供后期所需的生物量。参与生物量分配的器官包括叶子、节间、果、根等。叶既是源器官又是库器官。植物从公共池中根据每个器官的库强按比例分配生物量。

传统的基于过程的作物模型将公共池中的生物量按器官类别进行分配，例如叶子、节间、果等。大多数功能结构模型中生物量则按单个器官进行分配，因此计算复杂度高。GreenLab 模型中生物量根据器官的生长年龄、生理年龄和器官类别进行分配。同类器官簇中的器官分配相同的生物量，是一种介于完全按单个器官分配和按器官类别分配的中间方式，是计算效率和精细度之间的平衡。

4.2 植物需求

模型中植物的总需求是所有单个库器官的需求总和。不同生长年龄的需求与自动机产生的叶元及器官个数有关，由此可以建立生长模型与结构模型之间的联系。植物在年龄为t时的总需求D(t)通过式（4）计算。

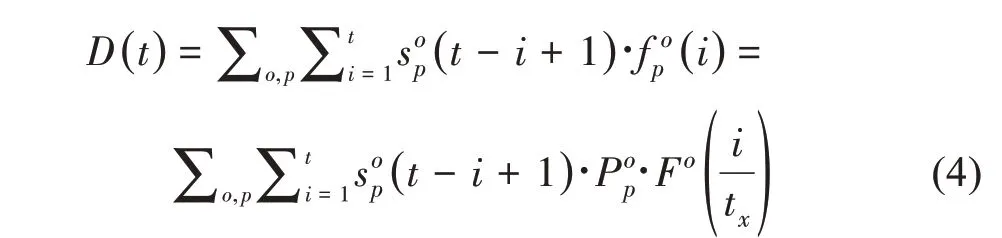
4.3 光合产量

GreenLab 模型认为生物量的生产与所截获的光成正比。与很多作物模型类似，作物的光截获采用比尔-罗伯特定律(Beer Lambert's law)进行计算。而其中的叶面积指数（LAI）进一步根据单株植物的叶面积S(t)以及植株的投影面积SP计算，如式（5）：

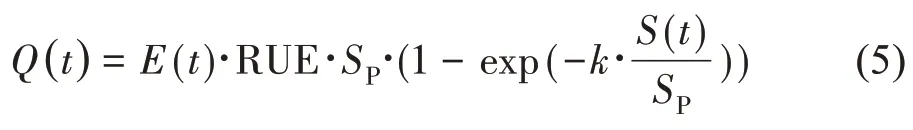
其中，E(t)为环境因子，RUE 为资源利用效率。为了突出反映主要环境因素的作用，可选择主要胁迫因子。例如对于温室作物，光为主要的胁迫因子，E(t)可选择为冠层上方的有效光合辐射，对应的RUE 为“光利用效率（Light Use Efficiency，LUE）”。对于大田作物，水为主要的胁迫因子，E(t)可选择为潜在蒸散，对应的RUE 为“水分利用效率（Water Use Efficiency，WUE）”。Q(t)为植物在周期t时产生的生物量，S(t)为植物的总叶面积，可由式（9）计算获得。在高种植密度时，SP与种植密度的倒数，即单株植物的平均面积接近。但是在低种植密度或者冠层尚未闭合时，SP表示的是植物占有的特征面积。在Green-Lab模型中，SP可作为模型的隐含参数计算得到。

4.4 器官生长

器官簇中生长年龄为i、生理年龄为p、类别为o的器官的生长取决于其自身的库强当前植物的需求D(t)以及上个周期供给的生物量Q(t-1)，如式（6）：

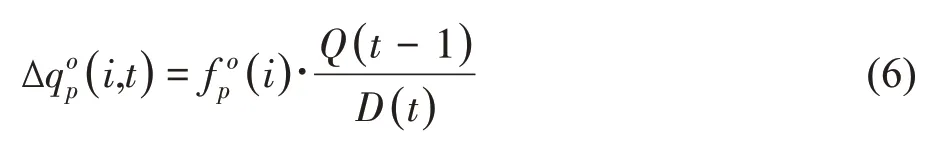
其中，Q/D常简称为源库比。但由于D无量纲，因此Q/D是有量纲的值，可理解为单位需求下的可用生物量。

将这类器官从出现以来的增量进行累加，即得到植物年龄t时生理年龄为p的器官o的（平均）总重可用列矩阵表示并通过矩阵形式计算，如式（7）：

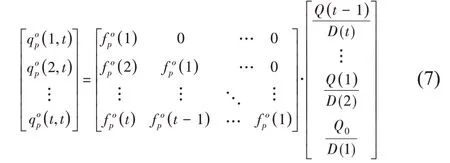
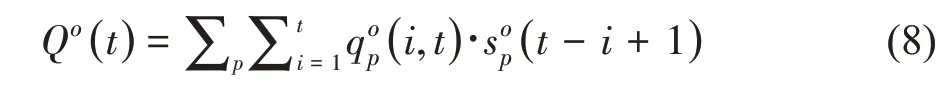
因此，GreenLab 模型可以根据需求输出单个器官的重或某类器官的总重，而后者是大多数基于过程的作物模型的输出结果。在拟合时，一般会同时拟合器官序列和器官总重。

植物的各个器官的大小可以基于各个器官的重，通过异速生长关系进行计算。特别地，对于叶子，通过引入比叶重（e,单位面积的叶片重），可建立叶子的重和其面积的关系。对所有功能叶面积（叶子年龄小于最大功能时间tb）求和得到植物的总叶面积，如式（9）：

4.5 递归计算

通过将叶面积的计算（式（9））表示为植物的生物量生产（Q）和需求（D）的函数，可得到GreenLab 模型的生物量的递归计算。由此可见，植物当前周期的产量取决于历史的产量和需求，如式（10）：

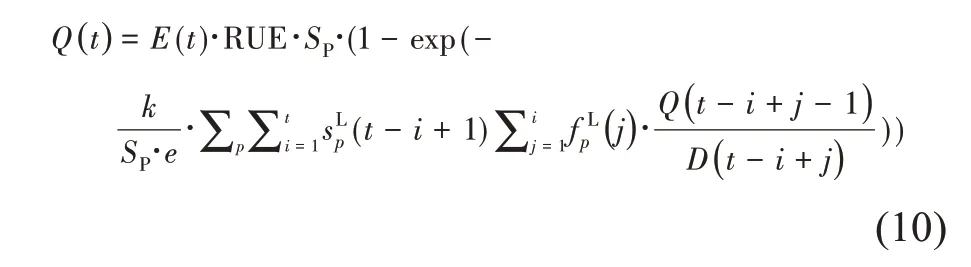
植物生长过程最终以离散的递归的动力学系统的形式表示，可以应用各种优化和控制方法，从而为GreenLab模型在农学上的应用提供了数学基础。

5 参数反求

模型中的部分参数如式（5）中的SP和RUE，以及器官的库强参数Po等，不易通过直接测量得到，因此通过拟合模型输出与直接可测的结果进行逆向反求。通常作物模型拟合的目标数据为器官总重。而作为器官水平的模型，GreenLab 还拟合单个器官水平的数据（器官序列），以反求器官的库强参数。

器官序列（Organ series）[17]定义为“在轴发育过程中，由同一初级分生组织产生的具有相同形态性质的所有器官（叶子、节间、果）”[24]。测量实际植物时，指将同类（相同生理年龄和生理年龄）的生长轴顶端或底端对齐后，取相同节位器官生物量的平均值即可得到拟合的目标数据。由于发育的随机性，同类生长轴往往包含不同的叶元个数。当拟合实际植物的数据时，通过最小化所采样植物的平均器官序列（观测值）以及根据潜在结构计算的平均器官序列（理论值）的差异来反求模型参数。

需要注意的是，式（7）所计算的为不同生长年龄的潜在器官序列。由于随机发育，有的生长单元未出现。如一个仍存活的生长轴的最大生长单元数为10，实际观测到8个生长单元，则位于轴顶部第3个生长单元的可能年龄为3到10之间的值。因此，在计算平均器官序列的理论值时，需结合潜在结构中的概率值进行计算[17]。假定实际测量的生长轴为顶端对齐求平均，由于每个生长单元的出现概率为b，则位于第K个位置的生长单元的生长年龄为i的概率PrK(i)服从截尾负二项分布NB(K,b)，可由式（11）计算：

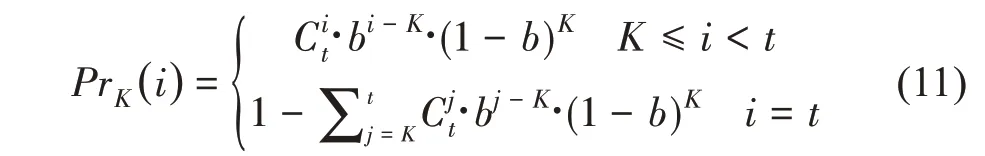
自上而下第K个位置的生长单元的年龄取值范围为[K,t]，基于此，自上而下第K个位置的生长单元的器官生物量的期望为：

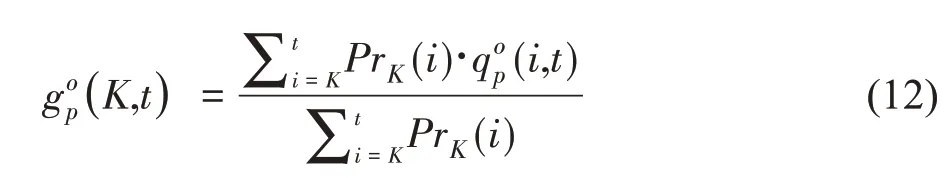
器官序列中包含了比植物总重更丰富的器官发育的信息。基于公共生物量池的假设，GreenLab 模型假设不同位置上的具有相同的生理年龄和生长年龄的器官具有相同的生物量，因此在构建实测的器官序列时，无需详细记录植物的拓扑结构信息。可测量的器官序列的重量中包含了历史的生长发育信息，因此模型能够基于单次测量的数据反求模型参数，即单阶段拟合（Single-fitting），重现植物的生长过程。在拟合时，通常按生理年龄、器官类别将植物分解为器官序列。不论植物分枝多少，器官序列的个数是有限的。以最大生理年龄为2、仅包含叶和节的咖啡树为例，拟合数据为四个序列：

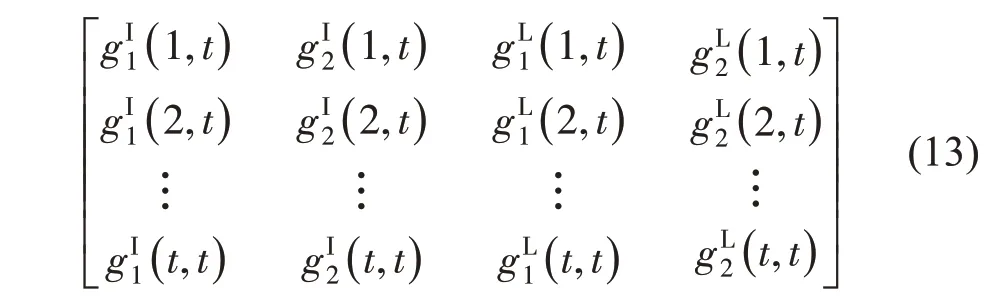
图3 所示为对14 棵同龄（2 年）的咖啡树的拟合结果。主茎的生理年龄为p=1，分枝的生理年龄为p=2。基于测量的数据反求了12 个模型的源库参数，基于这些参数模拟的咖啡树的结构如图3e。

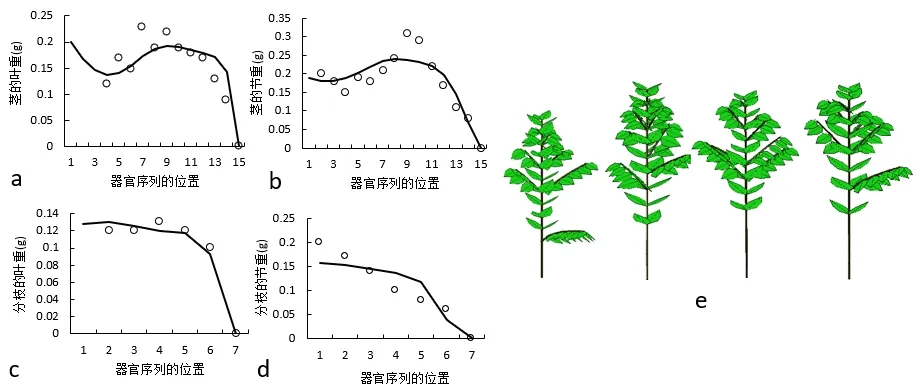
图3 通过GreenLab模型拟合的发育周期为16时的咖啡树的单阶段拟合（Gloups 软件）。‘○’代表观测值，‘─’代表理论值。a：茎的叶重；b：茎的节重；c：分枝的叶重；d：分枝的节重；e：咖啡树的三维形态展示Fig.3 Single-fitting of coffee tree with 16 DCs using GreenLab.‘○’represents observed values,‘-’represents computed values.a:leaf weight of stem;b:internode weight of stem;c:leaf weight of branch;d:internode weight of branch;e:3D structure of coffee tree(Digiplante software)

为提高参数的拟合精度，可以汇总多个生长阶段的数据进行拟合，即多阶段拟合（Multi-fitting）。图4为4 个发育阶段的拟南芥的多阶段拟合结果，基于测量的数据反求了6 个模型的源库参数。此例子中只有一种器官（叶子）但包含4 个器官序列，对应4 个阶段。可发现参数的变异系数减小。基于这些参数模拟的拟南芥的结构如图4c。

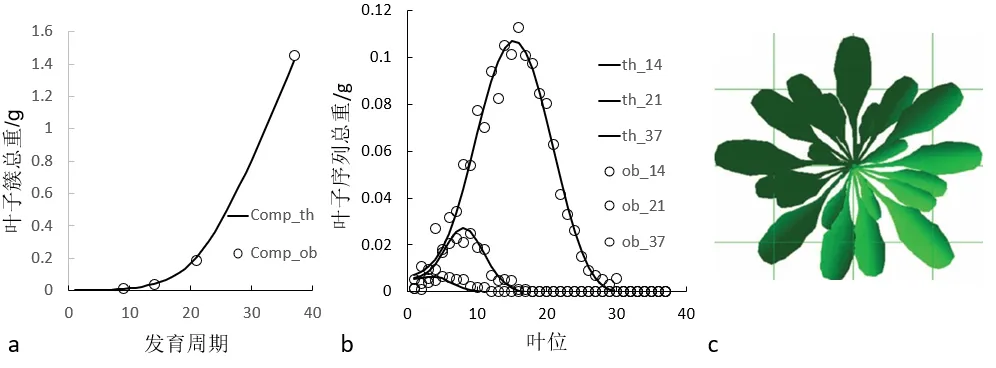
图4 通过GreenLab模型拟合的四个发育阶段（生长年龄9、14、21、37）的拟南芥的多阶段拟合（Gloups 软件）。‘○’代表观测值，‘─’代表理论值。a：叶子簇总重；b：叶子序列总重；c：拟南芥莲座的三维形态展示（Digiplante 软件）Fig.4 Multi-fitting(9,14,21,37 DCs)of Arabidopsis thaliana using GreenLab.‘○’represents observed values,‘-’represents computed values.a:weight of leaf cohort;b:weight of leaf organic series;c:3D structure of Arabidopsis thaliana(Digiplante software)

6 总结与展望

本文回顾了GreenLab 模型的关键概念，特别是近年来提出的通用拟合目标器官序列。GreenLab 模型一直以来所追求的目标，是能够基于植物观测和测量的数据进行参数反求和模型校准。模型的逻辑和结果建立于相关的概念和假设的基础之上，这些基本概念决定了如何对植物进行观察和采样，从而避免了无效数据的采集，节省人力和时间。对随机结构的植物进行采样测量，并通过最小二乘法获取模型的源库参数的方法，是一个非常具有挑战性的工作。器官序列提供了一种对于随机的植物结构进行采样、数据处理和拟合的方式，使得结构差异很大的植物都可采用共性的、与分枝数量无关的拟合数据来计算模型的参数。这点对于单株植物模型的应用是个突破。

随机模型的校准，第一步，通过冠顶分析方法，计算控制植物发育的概率（发育概率、存活概率、分枝概率），本文未作介绍。第二步，拟合基于潜在结构计算的理论器官序列值与基于植物枝条采样的实测器官序列值，从而通过优化方法计算控制植物生长的源库参数值。与之相对应的模拟软件也进行了迭代发展，包括Digiplante，GreenScilab，Qingyuan 等。最新的Gloups 软件可采用数组和遍历两种方式对各种植物进行模拟和校准[25]。其中，涉及不同植物结构的模拟、模拟结果和理论结果的对比、理论结果与实测数据的比较等，从模型理论和工程实现的角度都是很大的挑战，经历了长期的测试和研究。

基于器官序列的通用的参数反求方法为Green-Lab 模型在农学上的应用打下了基础。由于单株植物可能包含几十个或上百个器官，早期的模型应用需要进行大量的植物器官的大小和生物量的破坏性测量，费时费力。器官序列这个概念的提出为多分枝植物的采样提供了简化的方法。然而目前，虽然面向不同植物构建了模型，但仍限于给定环境下的作物生长，植物库的种类也比较有限。

植物表型技术[26]的迅猛发展，使得非破坏性地乃至自动地获取植物的结构和器官大小信息成为可能。同时物联网和传感器技术的发展，环境数据的获取也更便捷。通过数据和知识共同驱动的方式，可以更好地利用温光等环境数据和模型本身所包含的生态生理知识，深入理解植物与环境的关系，从而更好地预测植物的生长和产量[27,28]。植物的重建将不限于三维，还能加上时间维度，延伸到过去和未来。通过在线的植物本体和环境的监测、实际和虚拟植物的相互反馈，可以构建植物乃至生产系统的平行系统[29]，服务于精细的生产规划[30]以及植物工厂环境的自主控制[31]，空间生态保障系统模拟[32]以及未来气候变化的研究[33]等。