窄缝共振对波能装置-防波堤混合系统的影响
2021-12-26周斌珍李佳慧张恒铭臧军
周斌珍, 李佳慧, 张恒铭, 臧军
(1.华南理工大学 土木与交通学院,广东 广州 510000; 2.哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001; 3.巴斯大学 建筑与土木工程系,英国 巴斯 BA27AY)
高昂的发电成本严重制约了波浪能装置(wave energy converter, WEC)商业化规模的发展[1]。将WEC与其他海洋结构物结合是解决这一问题的有效途径[2-3]。可以实现发电功能与消波功能集成[4],有效地降低成本,促进WEC和防波堤的发展。
将振荡水柱式(oscillating water column,OWC)波浪能转换装置用于与防波堤结合是一种常见的集成方式[5]。现有WEC中,振荡浮子式WEC的转换效率较高[6],因此将振荡浮子式WEC与防波堤结合是另外一种常见的集成方式,但目前相关研究较少。根据浮体个数不同,可分为单浮体型WEC-浮式防波堤集成系统和双浮体型WEC-浮式防波堤混合系统。单浮体型集成系统由一个兼作WEC的浮式防波堤与功率输出装置(power take-off, PTO)连接组成。Chen 等[7]和Ning等[8]分别采用数值法和实验法对方箱型波浪能转换装置与防波堤集成系统的水动力性能进行了研究。Madhi等[9]的研究发现由非对称型的Berkeley-Wedge形集成装置的能量捕获效率在共振频率处达到了96.34%。可见浮子形状对单浮子集成系统的性能有显著影响。因此,Zhang等[10]选择了4个不同底部形状的单浮子型WEC-浮式防波堤集成系统,研究其浮子形状对集成系统水动力性能的影响。双浮体型混合系统由振荡浮子式WEC和浮式防波堤2个浮体组成。Ning等[11]应用解析法研究了双浮筒型WEC与浮式防波堤集成系统的性能,发现其波能转换性能和有效频率范围与单浮筒型集成装置相比有很大提高。Reabroy等[12]采用粘性计算流体动力学(computational fluid dynamics,CFD)软件模拟与实验相结合的方法,对一种海豚型波能装换装置与浮式防波堤混合装置的波能捕获效率进行了研究,结果表明最大发电效率为37.6%。Zhao等[13]通过实验研究了一种单浮体浮式防波堤型WEC与固定浮筒组成的新型系统,结果表明新型双浮筒系统的波浪能转换性能明显优于单浮体集成系统。
双浮体型混合系统与单浮体型集成系统最大的不同之处是2个浮体间存在窄缝共振现象。窄缝共振会改变2个浮体的受力,从而影响双浮体型混合系统的发电性能和防波性能,因此需要进一步研究。然而,目前关于窄缝共振的研究主要集中在2个固定浮体、没有PTO系统的固定浮体和运动浮体间以及没有PTO系统的运动浮体间的窄缝共振问题。如Li 等[14]利用完全非线性势流模型研究了2个并排驳船间的窄缝共振问题。为了精确模拟窄缝共振问题,一些研究人员还采用了一些粘性流体数值模型,如Jiang等[15]、Gao等[16]都应用OpenFOAM建立数值模型,研究了2个并排方箱之间的窄缝共振问题。此外,Zhao等[17]通过实验研究了2个固定的相同驳船之间的流体响应。
根据之前的研究无法确定窄缝共振对双浮体型振荡浮子式WEC和浮式防波堤混合系统发电性能和防波性能的影响。因此,本文应用粘性CFD软件Star-CCM+建立二维数值模型,对窄缝共振对双浮体型WEC-防波堤混合系统性能的影响开展研究,与单浮体型集成系统进行对比,并分析浮子运动和浮子间距对混合系统发电性能、防波性能以及窄缝间波高的影响。
1 数值模型建立
1.1 数值波浪水槽设置
为了模拟波浪与双浮体型WEC-防波堤混合系统的相互作用,本文使用Star-CCM+软件建立了一个二维数值波浪水槽,如图1所示,其x方向的长度为波长的6倍,z方向为水深的2倍。水槽分为造波区、工作区和消波区,造波区和消波区的长度均为波长L的1.5倍。因为Star-CCM+软件不能模拟纯二维平面模型,所以水槽y方向的宽度设为0.01 m,并且水槽的前后2个侧面采用对称面边界条件,保证水槽模型的二维性。
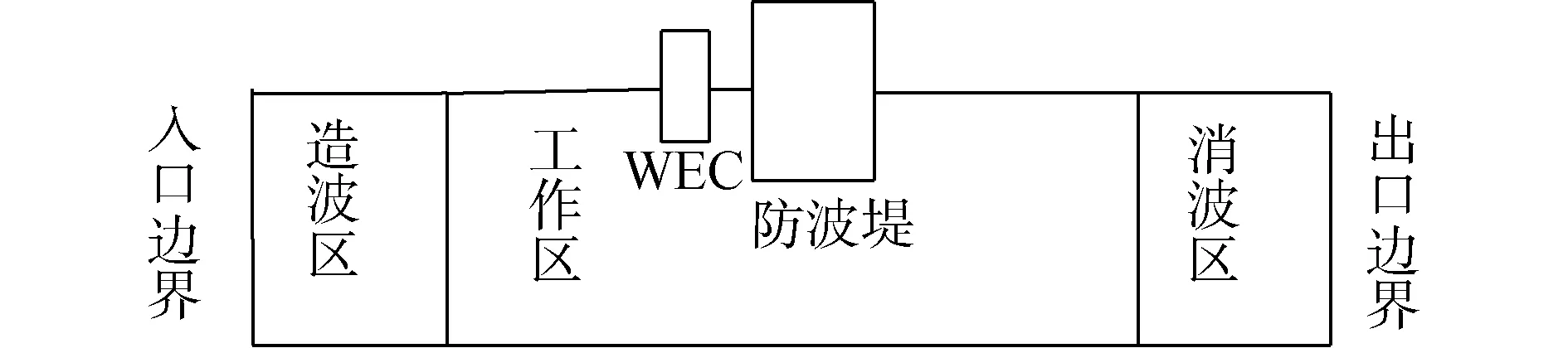
图1 二维波浪水槽模型Fig.1 Schematic diagram of 2-D wave flume model
由于防波堤的运动比WEC浮子的运动小很多,所以假设防波堤是固定的。WEC浮子做垂荡运动,与防波堤之间存在水动力耦合。水槽模型的入口和出口边界均设置为速度入口,顶部边界设置为压力出口。底部边界条件设置为壁面。为了消除反射波的影响,本文在入口和出口边界采用了力消波的方法,在浮子宽度较大的情况下,计算模型可以选用层流模型[10]。波浪水槽模型的网格划分方式设置为自动网格,选用切割体网格单元生成器来对液面加密区、液面过渡区、运动加密区和“Subtracted”区进行网格划分,生成的网格如图2所示。
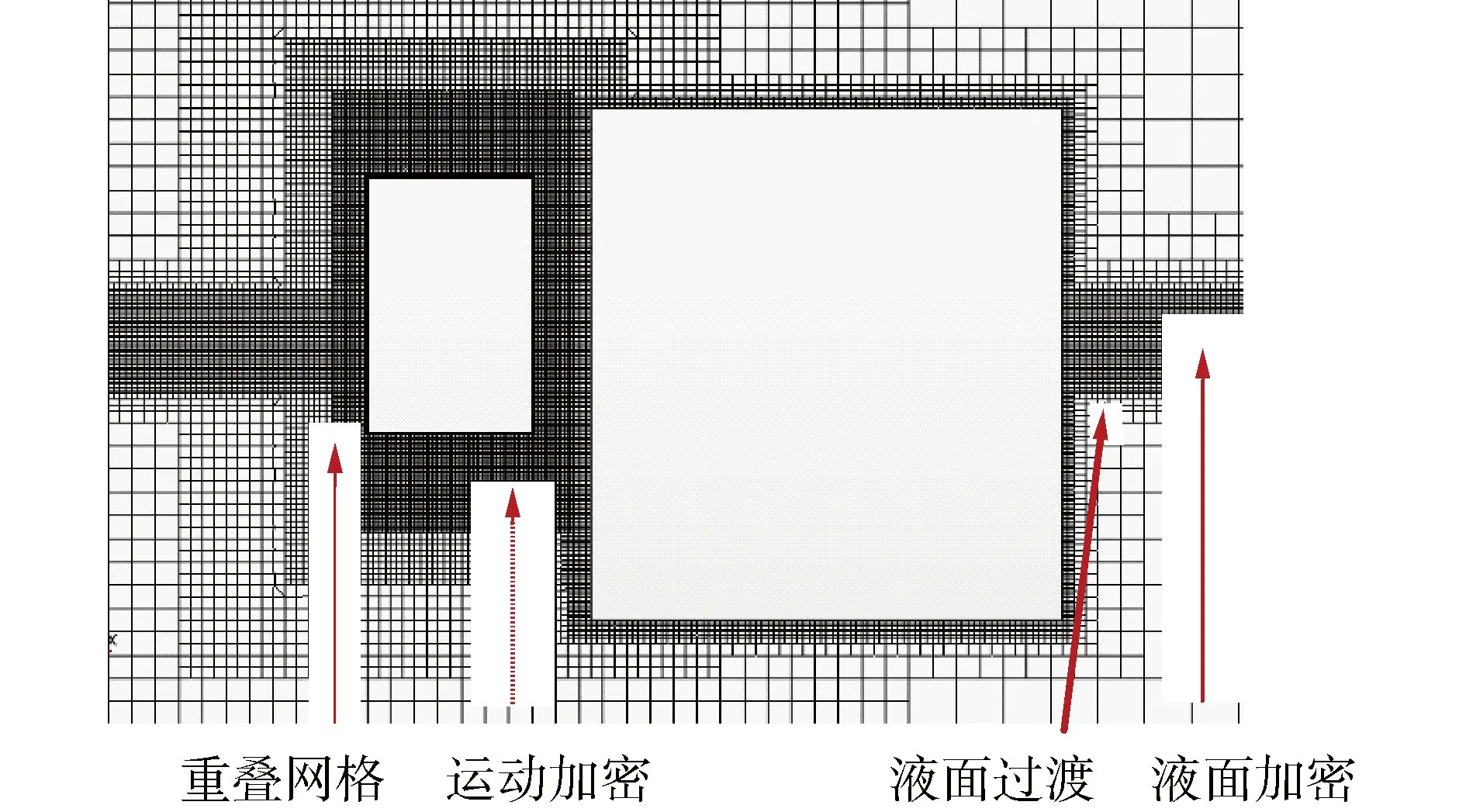
图2 模型网格布置Fig.2 Layout of model mesh
1.2 浮子运动方程与波能转换效率
假设波浪能转换装置为刚体,仅作垂荡运动。波浪能转换装置与防波堤之间无耦合运动,且不考虑系泊系统,则波浪能转换装置的运动方程可写为:
(1)
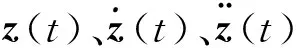
波能转换装置的发电性能通过转换效率ηe衡量,表达式为:
ηe=Ep/Ew
(2)
当波浪能转换装置只做垂荡运动时,平均波浪能转换速率Ep的表达式为[18]:
(3)
式中:n为波浪周期个数;T为波浪周期;t为时间;F为浮子所受PTO力;V为浮子的运动速度。
线性波的平均能量流动速率Ew[8]的表示式为:
(4)
式中:ρ为水密度,本文取1 023 kg/m3;g为重力加速度,本文取9.807 m/s2;Hi为入射波高;h为水深;Dy为波浪能装置y方向宽度;k为波数。
单个浮子单自由度运动的最优阻尼系数BOPT的表达式为[18]:
(5)
式中:az和bz分别为浮子垂荡方向附加质量和辐射阻尼;cz=ρgAw为恢复力系数;Aw为吃水面积;ω为波浪频率;当浮子后面存在防波堤时,az和bz分别为考虑了防波堤影响的浮子的附加质量和辐射阻尼。
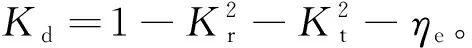
2 数值模型验证
在以往的研究[10]中,本文所采用的CFD模型的造波能力、水槽尺寸和网格收敛性已经得到验证,其中网格为Δz=H/20,Δx=2Δz,时间步长为Δt=T/1 000。
为了验证所采用的数值模型的准确性,本文应用所建立的数值模型对Jiang等[15]论文中的模型进行了模拟并进行对比。Jiang等[15]提出的由2个固定方箱组成的模型的宽度分别为B1=B2=0.5 m,吃水深度d1=0.103 m,d2=0.205 m,2个箱间距Bg=0.05 m,入射波高Hi和水深h分别为0.012 m和0.5 m。图3给出了本文数值模型结果与Jiang等[15]的结果的对比。
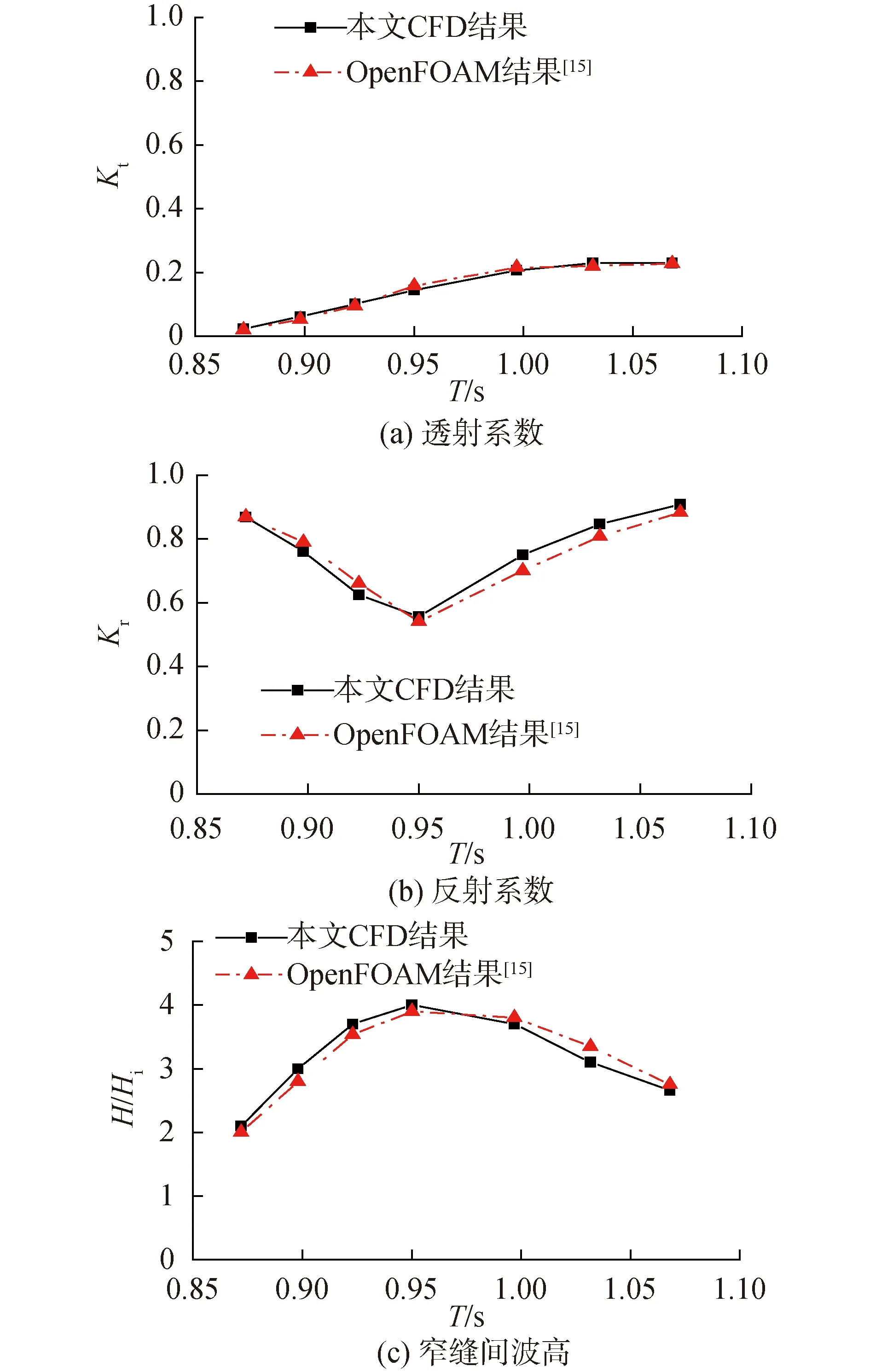
图3 本文CFD结果和OpenFOAM结果比较Fig.3 Comparison of CFD and OpenFOAM results
由图3可以看出,本文数值模拟计算得到的透射系数、反射系数和窄缝间波高与Jiang等[15]的结果吻合良好,验证了本文模型的正确性。
3 数值结果分析
3.1 不同模型性能对比
本节建立了单个防波堤、单个WEC和双浮体型WEC-防波堤混合系统3个模型进行对比研究。波浪水槽水深为h=3.0 m,入射波高为Hi/h=0.1。波浪能转换装置与防波堤之间的距离为Bd/h=0.083。波浪能转换装置的宽度为B1=0.7 m,吃水深度为d1=0.393 2 m,防波堤的吃水深度和宽度分别为D2=1.2 m和B2=2.0 m。
由图4(a)可知,双浮体型WEC-防波堤混合系统的透射系数远低于单个波浪能转换装置,在B1/L=0.085时最大降低82.9%。这是因为防波堤的吃水较大,使得双浮体型WEC-防波堤混合系统的防波性能得到了极大的提高。单个防波堤与双浮体型WEC-防波堤混合系统的透射系数基本一样,且都要比单个WEC的透射系数大。
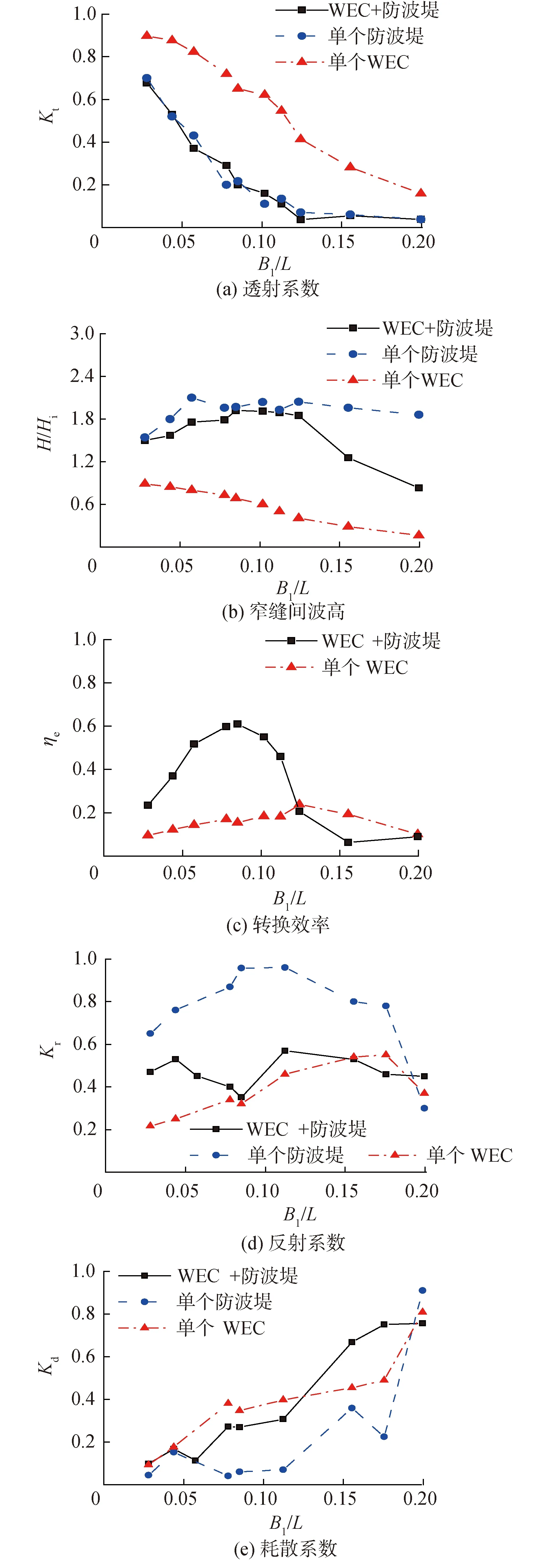
图4 最优PTO阻尼时不同模型的Kt、 Hg/Hi、 ηe、Kr和Kd随WEC宽度与波长比值B1/L的变化关系Fig.4 Variation of Kt, Hg/Hi , ηe and Kr with the ratio of WEC breadth to wave length B1/L of different models under optimal PTO damping
如图4(b)所示,双浮体型WEC-防波堤混合系统窄缝中的波浪共振发生在B1/L=0.085处,此时窄缝间波高达到最大值。图4(b)中单个WEC和单个防波堤时的窄缝波高是指原窄缝位置处的波面升高。在整个B1/L范围内,双浮体型WEC-防波堤混合系统窄缝间波高比单个防波堤相应位置处的波高小,但比单个WEC相应位置处的波高大得多。这是因为一部分入射波能量到达防波堤前被双浮体型WEC-防波堤混合系统的波浪能转换装置吸收了,导致双浮体型WEC-防波堤混合系统窄缝间的波高降低。此外,一部分通过波浪能转换装置的波浪被后面的防波堤反射,与通过波能转换装置的波浪叠加,增大了波能转换装置后的波高。
由图4(c)可知,由于双浮体型WEC-防波堤混合系统中防波堤反射的波浪能量会再次被波浪能转换装置吸收,因此双浮体型WEC-防波堤混合系统的转换效率要高于单个WEC。在B1/L=0.124时,单个WEC最大的转换效率为ηe=23.7%,而双浮体型WEC-防波堤混合系统的转换效率在B1/L=0.085时达到最大值,最大值为ηe=61%,比单个WEC提高了2.95倍,且高于对称型浮子50%的最大理论转换效率。由此可见,双浮体型WEC-防波堤混合系统的转换效率显著提高。双浮体型WEC-防波堤混合系统的共振周期大于单个WEC的共振周期,这是由于波共振导致最大转换效率对应的周期变大。
如图4(d)和图4(e)所示,单个防波堤时,由于防波堤吃水较大,本身的防波效果就很好,表现为大部分入射波的能量被反射回来,反射系数增大,一部分被耗散掉,仅有少部分波浪透射过防波堤;而对于双浮体型WEC-防波堤混合系统,有一部分入射波的波浪能被WEC浮子吸收,透射过WEC浮子的入射波的能量也同样因为防波堤吃水较大而大部分被反射回来,仅有一小部分透射过去,由于浮子的运动使得WEC-防波堤系统的耗散系数大于单个防波堤的耗散系数。同时,被防波堤反射回来的波浪能又再次被WEC浮子吸收,此时反射系数明显减小。
3.2 波能浮子运动的影响
浮子运动是影响双浮体型WEC-防波堤混合系统的重要因素之一。为了研究浮子的运动对装置产生的影响,本节设置了2个模型,2个模型中都包含WEC和防波堤,防波堤均固定不动,其中一个模型中WEC固定,另一个模型中WEC可运动。其他参数设置与3.1节相同。
图5给出了在最优PTO阻尼下,双浮体型WEC-防波堤混合系统和2个固定浮子模型的透射系数Kt和窄缝间波高Hg/Hi随WEC宽度与波长比值B1/L的变化关系图。如图5(a)所示,在浮子运动情况改变的条件下,其透射系数变化很小,这是因为透射系数与防波堤吃水密切相关,而这2个模型的吃水相同。

图5 最优PTO阻尼时不同混合系统模型的Kt和Hg/Hi随WEC宽度与波长比值B1/L的变化关系Fig.5 Variation of Kt and Hg/Hi with the ratio of WEC breadth to wave length B1/L for different hybrid system models under optimal PTO damping
由图5(b)可知,窄缝间波高随着B1/L的减小而先增大后减小,2个固定浮子的窄缝间波高比一个前端运动浮子和一个后端固定浮子的大,但2个固定浮子的窄缝间共振周期比一个前端运动浮子和一个后端固定浮子的小。
3.3 浮子间距的影响
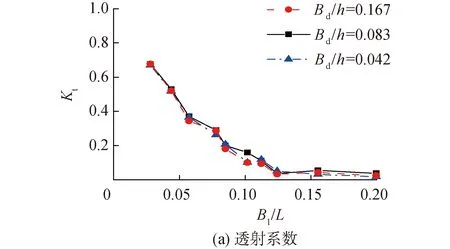
与单个WEC相比,浮子间距是双浮体型WEC-防波堤混合系统特有的参数。为了研究浮子间距对双浮体型WEC-防波堤混合系统性能的影响,本节研究了最优PTO阻尼下浮子间距为Bd/d=0.042,0.083和0.167的双浮体型WEC-防波堤混合系统的透射系数Kt、窄缝间波高Hg/Hi、转换效率ηe、反射系数Kr和耗散系数Kd随B1/L的变化,如图6所示。该系统的其他参数与3.1节中模型的参数相同。
如图6(a)所示,不同浮子间距的双浮体型WEC-防波堤混合系统的透射系数十分接近,这是因为双浮体型WEC-防波堤混合系统的浮子和防波堤吃水保持不变,只改变了浮子间距。
如图6(c)和(e)所示,在0.573 1)与单个WEC相比,双浮体型WEC-防波堤混合系统转换效率在大部分B1/L的范围内显著增加,最大转换效率发生在窄缝间波浪共振时。 2)WEC的运动导致双浮体型WEC-防波堤混合系统窄缝间的波高减小、共振周期增大,对透射系数影响很小。 3)双浮体型WEC-防波堤混合系统窄缝中的波浪共振周期和最大波高随窄缝间距的减小而减小,最大能量转换效率随间隙距离的减小而增大。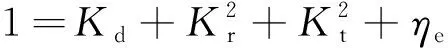
4 结论
