仿生尾缘对导管桨推进性能的影响

尚志强， 刘鹏， 王思琦， 刘然然， 刘福顺， 王许洁

(1.中国海洋大学 山东省海洋工程重点实验室，山东 青岛 266100； 2.河口黄河河务局，山东 东营 257231)

导管螺旋桨又称套筒螺旋桨，与普通螺旋桨不同的是外部多了一个套筒，导管的剖面分为折线型和机翼型。导管桨相比螺旋桨来说，能够改善船尾伴流场，提高额外推力和推进效率。因此，导管桨在船舶上广泛应用。

国内外对导管桨水动力性能方面做了大量的研究。吕晓军等[1]研究了不同网格模型和湍流模型下导管桨的正车敞水性能曲线。胡健等[2-3]研究了导管桨内部流场数值特征，并探究了不同导管长度、叶稍间距和斜流对导管桨水动力性能的影响。谢永和等[4-5]研究了导管的长径比、伸张系数和收缩系数以及导管型号对导管桨水动力性能的影响。Sanchez-Caja等[6]用计算流体力学方法分析了导管桨的水动力性能。Feiten等[7]等采用实验的方法对导管桨进行了充分的研究。宋科等[8]探究了多导管螺旋桨的水动力性能。高慧等[9]探究了导管桨加上毂帽鳍后的节能性能。Caldas等[10]计算了不同舵分布下导管桨的操纵性以及其水动力性能。张正骞等[11]、孙瑜[12]等依据仿生学原理，研究了仿生导管桨的水动力性能。

本文以Ka4-5508+JD75导管桨为研究对象，利用Fluent对其水动力性能进行分析计算，将计算值与文献[13]的实验值对比，验证这种复杂结构混合型网格划分方法的可靠性。然后依据仿生学原理，以该桨为母型，利用三维建模软件UG在导管后半段增加锯齿突起，结合复杂结构混合型网格划分方法在Gambit完成网格划分，在Fluent软件中实现对该仿生尾缘导管桨的水动力性能模拟，结合控制变量方法研究尾缘突起个数、尾缘长度和尾缘倾斜角度对仿生尾缘导管桨水动力性能的影响，并探究其水动力性能提升的机理。

1 数值方法与计算模型

1.1 数值计算方法

假设流体是不可压缩的，本文采用RANS方程(雷诺平均方程)作为求解旋转域的控制方程[14-15]，流场的连续性方程和动量方程可分别表示为：

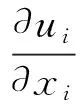
(1)

i,j=1,2,3

(2)

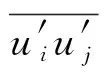
本文使用的SSTk-ω[16-17]模型，综合了k-ω模型在近壁区计算的优点和k-ε模型在远场计算的优点。与标准k-ω模型相比，SSTk-ω模型中增加了横向耗散导数项，同时在湍流黏度定义中考虑了湍流剪切应力的输运过程，模型中使用的湍流常数也有所不同。这些特点使得SSTk-ω模型的适用范围更广。

1.2 模型建立与网格划分

本文研究采用的计算模型由JD75导管和Ka4-5508螺旋桨组成。螺旋桨直径D=0.25 m，叶稍间隙1 mm，桨叶数4，盘面比为0.55，螺距P=0.2 m，相应螺距比P/D=0.8。图1给出了Ka4-5508螺旋桨和JD75导管的模型以及改进后的仿生尾缘导管桨模型。借用三维建模软件UG对JD75导管后半段进行改进，以导管后半段母线为基准线，改变仿生尾缘伸出距离为α，仿生尾缘倾斜角度为β，仿生尾缘突起个数为γ。

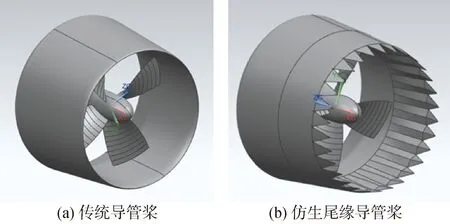
图1 改进前后的导管桨模型Fig.1 Before and after improved of ducted propeller model

对于图1(a)中的传统导管桨，将导管桨的数据点导入Gambit中建模。由于导管内壁和螺旋桨叶稍间距很小，为了提高计算效率和保持相对较高的计算精度，并且基于复杂结构混合网格划分方法,需对求解域进行更加细致地划分。将求解域划分为导管前、包含导管和桨的中部区域、导管后3个部分，然后又将包含导管和桨的中部区域划分为含螺旋桨的单独网格部分、含导管的网格部分和其余部分。为了后续划分网格的需要，除螺旋桨所在域以外的部分分割成对称结构体。如图2所示，整个流场域大小一共61个体积，共220万网格。计算域入口与桨盘面的距离为3D，计算域出口与桨盘面的距离为4D，计算域直径为3D[18]。

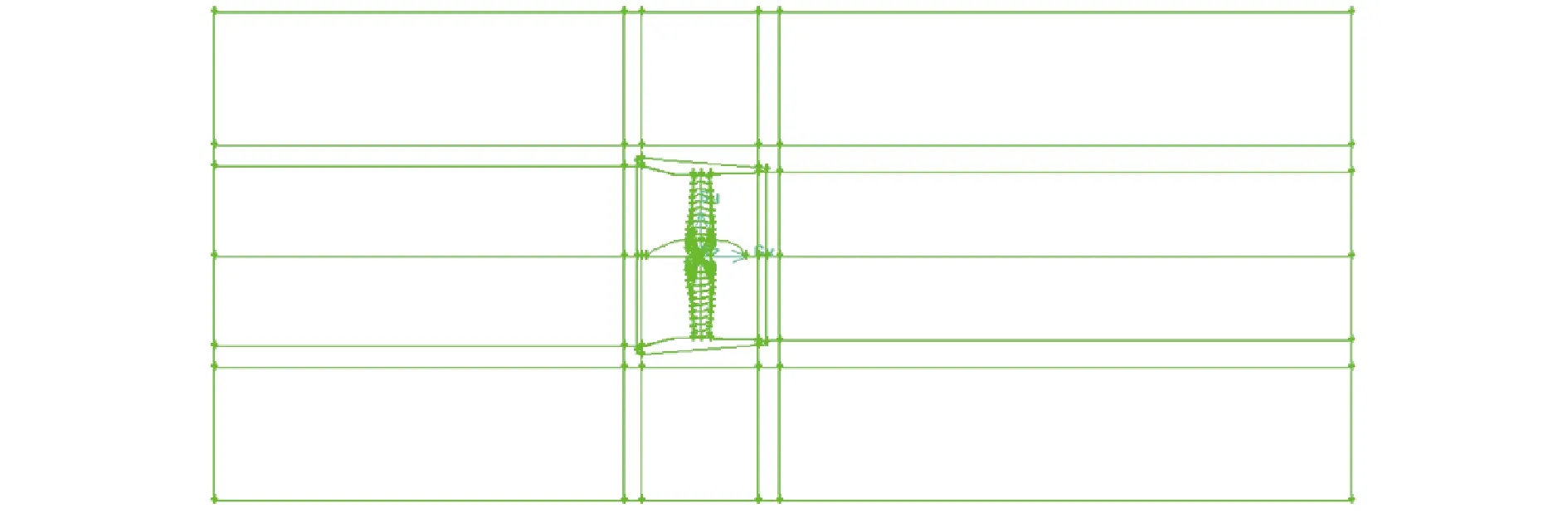
图2 网格分块划分示意Fig.2 Schematic diagram of grid division

包含螺旋桨的域为动域，其余部分为静域。动域的网格为非结构性四面体网格，如图3(a)所示；对桨叶叶梢部分进行网格加密，导管前后缘采用Cooper的方式划分体网格，由于导管内壁和螺旋桨叶稍间距很小，该部分采用结构网格并进行加密，其余部分均采用结构性网格，进流段和出流段适当降低网格数，如图3(b)、(c)所示。这样，在网格模型总节点数一定的情况下可以提高计算精度，还可以避免流场变化平缓区域计算资源的浪费。

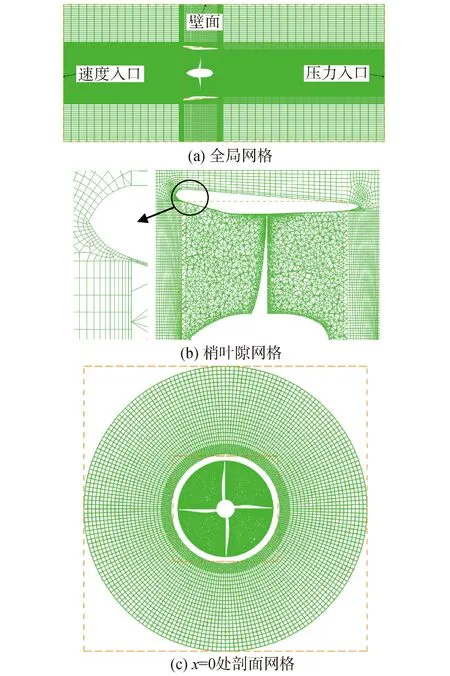
图3 计算域的全局网格、梢叶隙网格及x=0处剖面网格Fig.3 The meshing of all domain, blade tip and section x=0

1.3 边界条件及求解参数的设定

在螺旋桨敞水计算中，大域的入口边界设置为速度入口；出口边界设置为压力出口；圆筒表面边界设置为壁面；导管和螺旋桨表面设为无滑移、固壁边界条件，如图3(a)所示。螺旋桨所在的动域采用MRF (moving reference frame)方法，并绕x轴以600 r/min的速度旋转，通过改变来流速度改变进速系数。使用Fluent软件基于有限体积法求解RANS方程，湍流模型为SSTk-ω，采用三维单精度基于压力隐式求解器，耦合方式采用SIMPLER算法，压力项采用PRESTO方式，离散格式采用二阶迎风格式，对导管桨的定常水动力性能进行计算，计算结果收敛后停止迭代。

2 数值验证

分别取进速系数为0.1～0.7，螺旋桨转速为600 r/min。通过Fluent软件模拟其水动力性能，各系数定义表示为：

(3)

(4)

(5)

KT=KTp+KTd

(6)

螺旋桨推进性能为：

(7)

式中：KTp和KTd分别为螺旋桨和导管的推力系数；KQ为螺旋桨的转矩系数；KT为导管桨的推力系数，Tp和Td分别为螺旋桨和导管的推力，N；Q为螺旋桨的转矩，N·m；η为导管桨效率；J为进速系数；VA为来流速度，m/s；n为转速，r/min；D为螺旋桨直径，m；ρ为水的密度，kg/m3。

将计算值与实验值相比较，结果如图4所示。由图4可知，计算值和实验值曲线走向一致，呈现相同的变化规律，随着进速系数的增加，推力系数和扭矩系数均减小，两者误差的绝对值也增大，效率误差最大不超过3%，所对应的进速系数J=0.5。推力系数和扭矩系数的误差较高的计算结果均出现在高进速系数情况下(J≥0.5)，而在低进速系数时，计算结果的误差均低于8%。

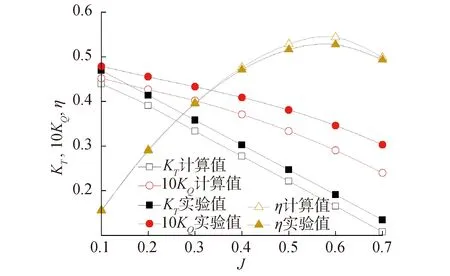
图4 Ka4-5508+JD75导管桨敞水性能Fig.4 Open water performance of Ka4-5508+JD75 ducted propeller

存在误差的原因主要由2个部分构成：一是数值模型和实验模型存在出入，在Gambit中建模时，生成的桨叶和桨毂较为简单粗糙，这也就导致了与实验模型存在一定误差。同时数值计算过程中离散方程的截断误差以及舍入误差也是不容忽略的，实验设备以及实验条件的设置也能够引起误差。二是利用Fluent软件模拟螺旋桨的敞水性能是在理想状态下进行的，这在现实中是不可能达到的，实验中的水面兴波以及水池壁面等因素的影响并没有考虑到。

总的来说，利用以上提出的数值模拟方法模拟导管桨的水动力性能是可行的，满足模拟精度要求。

3 仿生尾缘导管桨水动力特性及影响因素分析

采用上文提出的基于复杂结构混合型网格划分方法，选取α=0.2L(L为导管长度)，β=6°，γ=30作为仿生尾缘导管桨的初始参数，采用控制变量的方法来探究参数对仿生尾缘导管桨水动力性能的影响。

3.1 尾缘突起个数

改变尾缘突起个数γ分别为20、24、30、36，固定α=0.2L，β=6°，探究尾缘突起个数的改变对导管桨推力系数、扭矩系数和效率的影响，如图5所示，图中“Duct”表示尾缘未改进导管桨的相应性能曲线。

从图5(a)中可以看出改变仿生尾缘突起个数后的推力系数较传统导管桨有较大提升，随着进速系数提高，推力系数增长速度增大，最大值出现在γ=20、J=0.7时为25%。尾缘突起个数的改变对推进系数的影响很小，整体上看随着尾缘突起个数的增加，推力系数略微减小。

从图5(b)中可以看出改变仿生尾缘突起个数后的扭矩系数较传统导管桨同样有较大提升，随着进速系数提高，扭矩系数增长速度增大，但增长的幅度较推力系数小，最大值出现在γ=20、J=0.7时为19%。从整体上看，随着尾缘突起个数的增加，扭矩减小，低进速系数下扭矩减小的幅度相比较于高进速系数更大。

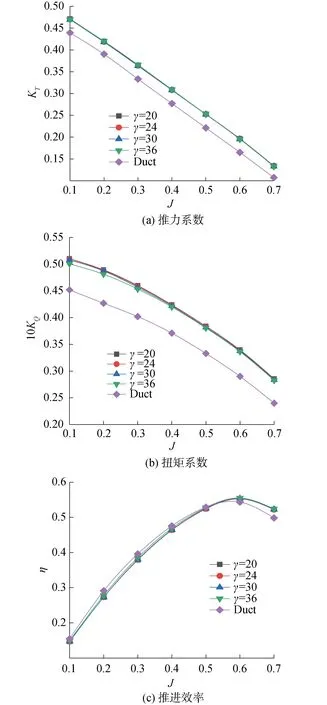
图5 不同尾缘突起个数的敞水性能曲线Fig.5 Open water performance of different number of trailing edge protuberances

从图5(c)中可以看出低于J=0.5时，传统导管桨的效率高于仿生尾缘导管桨的效率，随着进速系数增加，仿生尾缘导管桨与传统导管桨效率的差值减小。大于J=0.5情况下，仿生尾缘导管桨效率高于传统导管桨，最大值为5.16%出现在γ=36、J=0.7时。当进速系数J>0.5时，效率随着突起个数的增加而增加。

由此得出结论：突起个数的变化对推力系数和扭矩系数影响不大，当J>0.5时仿生尾缘导管桨的效率高于普通导管桨的效率，J<0.5时，反而低于普通导管桨的效率，起到不利的影响。

3.2 尾缘长度

改变尾缘长度α分别为0.1L、0.15L、0.2L、0.25L、0.3L，固定β=6°，γ=30，探究尾缘长度的改变对导管桨推力系数、扭矩系数和效率的影响，如图6。

从图6(a)中可以看出改变仿生尾缘长度后的推力系数较传统导管桨有较大提升，随着进速系数提高，推力系数增长速度增大，最大值出在α=0.3L、J=0.7时为25.57%。尾缘长度的改变对推进系数的影响很小，整体上看随着尾缘长度的增加，推力系数增加的幅度很小。

从图6(b)中可以看出改变仿生尾缘长度后的扭矩系数较传统导管桨同样有较大提升，随着进速系数提高，扭矩系数增长速度增大，不过增加的幅度较推力系数小，最大值出在α=0.3L、J=0.7时为18.9%。从整体上看，随着尾缘长度的增加，扭矩增加幅度很小。

从图6(c)中可以看出低于J=0.5时，传统导管桨的效率高于仿生尾缘导管桨的效率，随着进速系数增加，仿生尾缘导管桨与传统导管桨效率的差值减小。大于J=0.5情况下，仿生尾缘导管桨效率高于传统导管桨，最大值为5.6%出现在α=0.3L、J=0.7时。在进速系数J>0.5情况下，随着尾缘长度的增加，效率也小幅度增加。

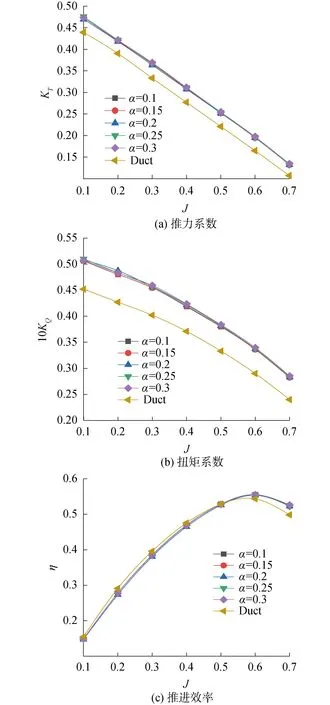
图6 不同尾缘长度的敞水性能曲线Fig.6 Open water performance of different trailing edge lengths

由此得出结论：尾缘长度的变化对推力系数和扭矩系数影响不大，在J>0.5时，能够提高效率，J<0.5时，低于普通导管桨的效率。

3.3 尾缘倾斜角度

改变尾缘倾斜角度β分别为2°、4°、6°、8°、10°，固定α=0.2L，γ=30，探究尾缘倾斜角度对导管桨推力系数、扭矩系数和效率的影响，如图7所示。

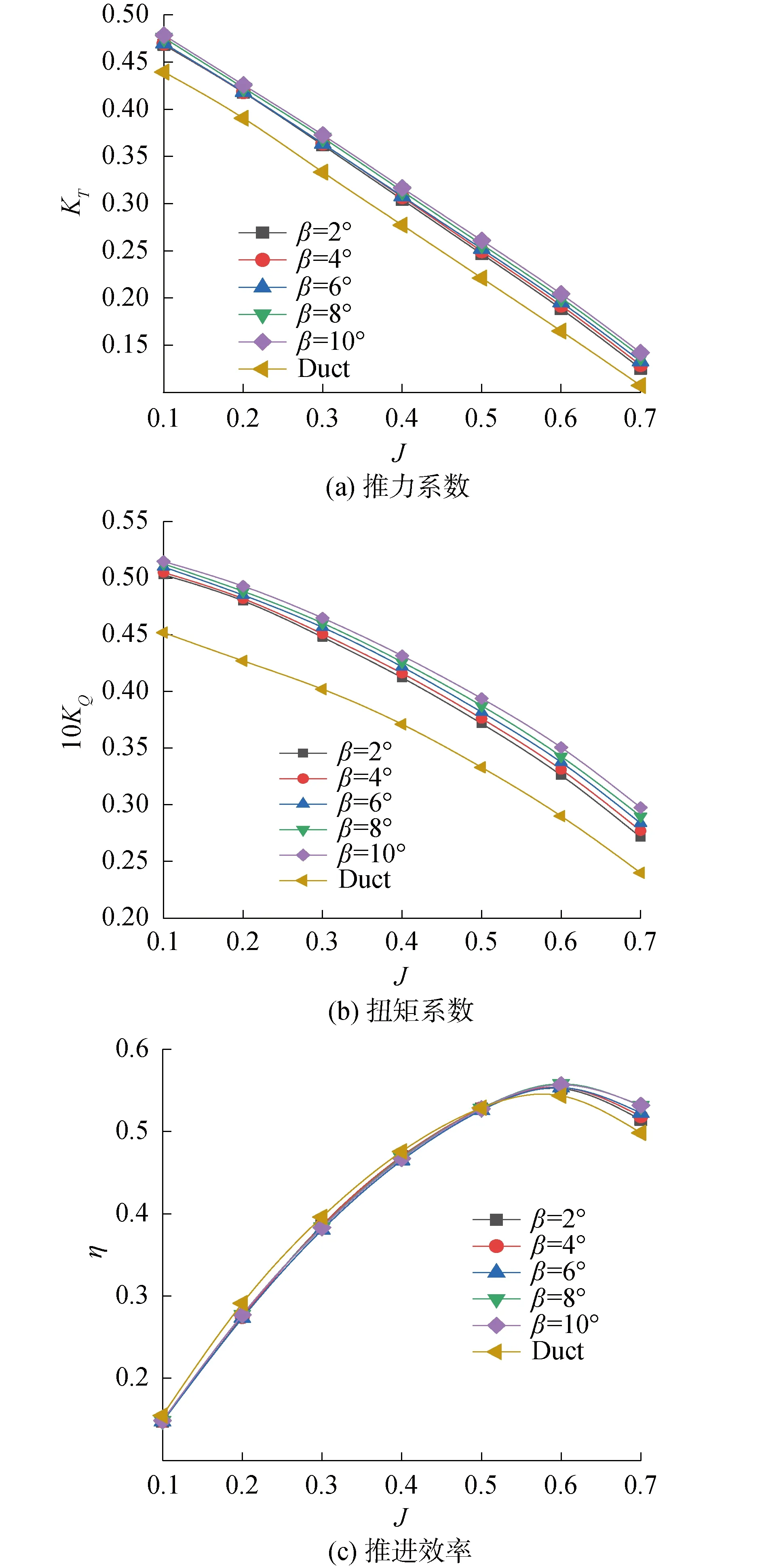
图7 不同尾缘倾斜角度的敞水性能曲线Fig.7 Open water performance of different trailing edge inclination angles

如图7(a)所示，改变仿生尾缘倾斜角度后的导管桨的推力系数较传统导管桨有较大提升，随着进速系数的增加，推力系数增长速度增大，最大值出在β=10°、J=0.7时为32.4%。随着尾缘倾斜角度的增加，推力系数增加，增加的幅度比图5(a)和图6(a)中的幅度大。

如图7(b)所示，改变仿生尾缘倾斜角度后的扭矩系数较传统导管桨同样有较大提升，随着进速系数提高，扭矩系数增长速度在增大，最大值出在β=10°、J=0.7时为24%。随着尾缘倾斜角度的增加，可以明显地看出扭矩系数在增加，增加的幅度较图5(b)和图6(b)中更明显。

如图7(c)所示，低于J=0.5时，传统导管桨的效率高于仿生尾缘导管桨的效率，随着进速系数增加，仿生尾缘导管桨与传统导管桨效率的差值在减小。大于J=0.5情况下，仿生尾缘导管桨效率高于传统导管桨，最大值为6.7%出现在β=10°、J=0.7时。在进速系数J>0.5情况下，随着尾缘长度的增加，效率在增加。

由此得出结论：尾缘倾斜角度的变化对推力系数和扭矩系数的影响比较明显，随着倾斜角度增加，推力系数和扭矩系数也在增加，对效率的影响与3.1节和3.2节中相同，不过效率增加速度较前2种工况更快。当角度继续增加时，水流冲击仿生尾缘的载荷增大，相应齿根应力的增加可能导致螺旋桨的损坏，同时高流速下易产生空泡影响仿生尾缘水动力性能。因此，目前只在尾缘倾斜角度的有限范围内进行计算。后续研究中，将把推进性能、结构强度以及空泡性能综合考虑进行分析。

3.4 桨叶压力分布对比

图8是J=0.7、来流速度1.75 m/s、螺旋桨转速600 r/min时的桨叶压力图。对比分析改进前后的桨叶压力分布图，得到推力增加的机理，图8是改进前和改进后(α=0.2L、β=10°、γ=30个)的桨叶压力分布图。

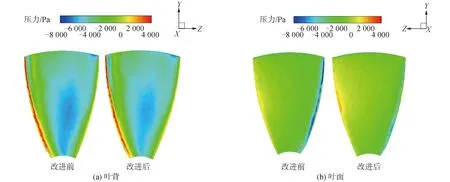
图8 J=0.7 时导管改进前后桨叶压力分布对比Fig.8 Comparison of blade pressure distribution before and after duct improvement at J=0.7

观察图8可以看到导管改进后对叶背压力分布影响较小，仔细对比观察后发现导管改进后的叶背压力分布更均匀，中心处的低压区明显减小。相比之下，导管改进后的叶面随边的高压区扩大，导边的低压区减小，桨叶上的压力分布变化导致推力增大。另外通过压力分布对比，导管改造后低压区减少，最低压力值提升，这样有利于减缓空泡的发生和螺旋桨运行的噪声。

3.5 流场x轴方向速度分布

图9是J=0.4、来流速度1.0 m/s、螺旋桨转速600 r/min时的桨叶压力图。

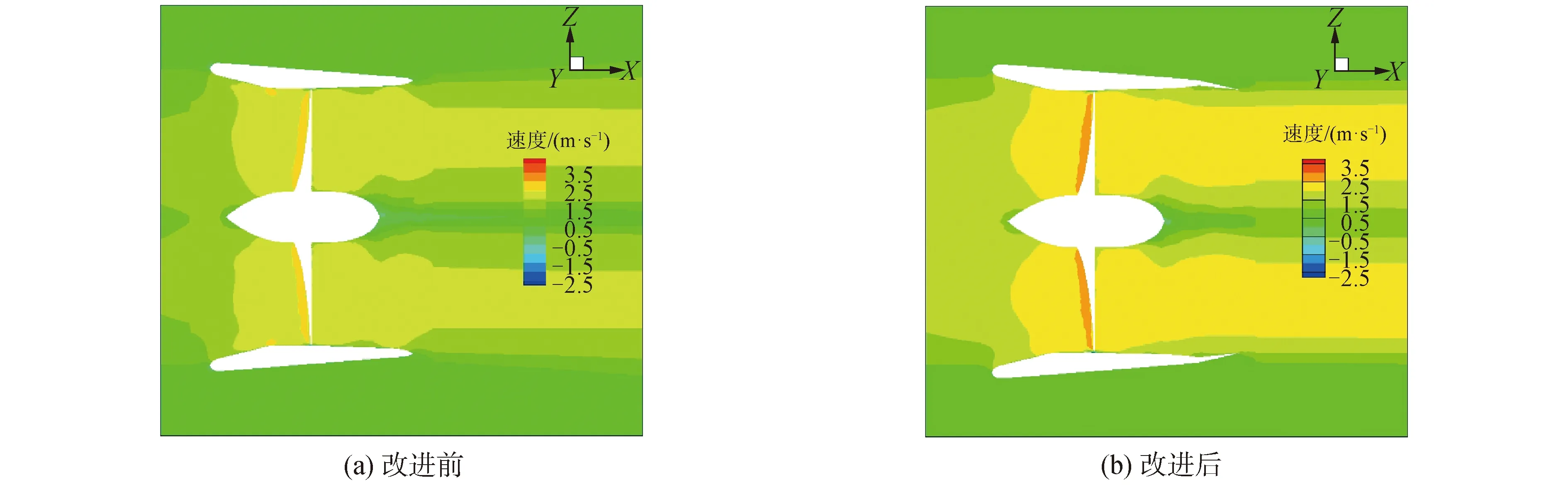
图9 J=0.4时导管改进前后X轴速度分布对比图Fig.9 Comparison of X-axis velocity distribution before and after improvement of duct at J=0.4

对比改进前后x轴速度分布对比图发现：导管改进前，x轴方向的速度分布数值绝大多数在2.0～2.5 m/s；而导管改进后，x轴方向的速度分布数值绝大多数在2.5～3.0 m/s且速度分布面积扩大。因此，导管改进后，流场得到改善，导管桨的推力相应增加。

4 结论

1)通过应用计算流体力学中的SSTk-ω模型和旋转坐标系方法，基于复杂结构混合型网格划分方法，在Fluent软件中实现对导管桨的数值模拟，对比计算值和实验值，验证这种混合型网格划分方法的可靠性。

2)通过分析导管桨改进前后的水动力性能曲线和压力、速度分布图，发现：该仿生尾缘导管桨相比传统导管桨来说，推力系数和扭矩系数均有较大提升，效率在高进速系数有提升；改进后的叶背压力分布更加均匀，导管改造后低压区减少，最低压力值提高，有利于减缓空泡的发生和螺旋桨运行的噪声；导管改进后，x轴方向的速度增加，流场得到改善，导管桨的推力得到增加。

3)该仿生尾缘导管桨更适用于高进速系数的船舶，能够提高效率起到有利影响，符合绿色船舶的发展趋势，低进速的船舶不建议采用此改进方式。

在接下来的研究中，可以选择最优模型开展敞水实验，以及针对噪声和不同导管桨模型开展研究。