废石-尾砂胶结膏体料浆触变性试验研究与分析
2021-12-25杨天雨乔登攀
杨天雨,乔登攀,王 俊,张 希
(1.昆明理工大学 国土资源工程学院,昆明 650093;2.玉溪矿业有限公司,云南 玉溪 653100)
触变性亦称摇变,是指物体(如油漆、涂料)受到剪切时稠度变小,停止剪切时稠度又增加或受到剪切时稠度变大,停止剪切时稠度又变小的一“触”即“变”的性质。触变性是一种可逆的溶胶现象,代表流体黏度对时间的依赖性[1]。杨美卿[2]通过高倍电子显微镜研究了细颗粒浆体,发现细颗粒浆体中确实存在着絮团絮网结构。而且这些结构具有多种层次,联系脆弱,在外力作用下结构很易破坏,在卸掉外力时又很易搭接。膏体料浆是不同粒级的尾砂、水泥和水的混合物,有时还包含一些添加剂(絮凝剂)等材料。因此,浆体中含有大量细颗粒,颗粒表面的物理化学作用导致浆体内部存在一定强度的絮网结构[3],具有明显的触变性质。膏体触变性的研究对其制备、输送以及地表堆存等工艺具有十分重要的意义。王庆伟等[4]研究了赤泥浆体的触变行为,探讨了触变性对干式排放过程中的影响及应用。何哲祥等[5]通过研究认为细颗粒骨料与水泥等固体材料组成的混合物料是一种触变流体,提出了充填料浆的活化搅拌技术。应力松弛及剪切稀化效应是触变性的两种表现形式,即随着剪切强度及剪切时间的增加,浆体内部结构破坏加剧,浆体的剪应力及表观黏度会随着剪切时间的增长而持续递减,最后趋近于平衡状态。NGUYEN等[6]在对高浓度赤泥流变性质的研究中发现,浆体表观黏度随剪切时间逐渐减小,最终趋于稳定值。PORNILLOS[7]对不同搅拌时间尾矿膏体的屈服应力进行了测试,结果表明:屈服应力值随搅拌时间逐渐减小,最终趋于平衡状态。韩文亮[8]在对细颗粒浆体的研究中,发现了明显的应力松弛现象。陈琴瑞[9]对羊拉铜矿全尾膏体的研究发现,表观黏度及屈服应力随时间逐渐减小,最终趋于一恒定值。
但是目前研究仅是在发现现象的基础上进行了简单的定性分析,没有建立起定量的数学模型对其进行描述。本文通过对膏体料浆进行应力松弛试验,分析膏体料浆屈服应力的触变规律,并构建膏体料浆屈服应力的触变模型来定量描述膏体料浆的触变性。
1 充填膏体的应力松弛试验
1.1 试验材料
本次试验的试验材料选用某矿山废石尾砂,尾砂松散堆积密度1.328 t/m3,表观密度2.841 t/m3,堆积密实度为0.468,空隙率为0.532,加权平均粒径dp为57.78 μm,尾砂化学成分见表1。本次试验所用废石采用该矿山露天采场矿体下盘剥离废石,废石以白云岩为主,平均密度为2.754 t/m3,松散堆积密度1.75 t/m3,堆积密实度为0.635 5,空隙率0.364 5;水泥采用普通硅酸盐425#水泥。

表1 尾砂化学成分表
1.2 试验方案
试验设计膏体料浆浓度为75%、76%、77%、78%、79%,废石尾砂比为5∶5和4∶6,剪切速率设定为30、60、90、120 s-1,共计40组试验。
首先,编写流变仪加载程序,流变仪设定为恒剪切速率的模式,试验时配置1 000 mL料浆,为消除水泥水化反应对试验结果的影响,每进行完一次剪切试验,需重新配制料浆。其次,为使料浆与实际情况更加接近,在剪切开始之前,需进行10 s的预剪切,并静置10 s,随后按照程序设定的30、60、90、120 s-1进行剪切试验,剪切时间为1 200 s,试验加载程序如图1所示。
1.3 试验结果与分析
应力松弛法流变试验结果如图2和图3所示,并对四个剪切速率条件下触变前后的剪切应力值进行宾汉回归,求得触变前后的屈服应力和塑性黏度。由于篇幅限制,仅列出废石尾砂5∶5、质量浓度79%和废石尾砂4∶6、质量浓度79%的膏体料浆的试验结果曲线。
从图2和图3可以看出,膏体料浆的剪切应力随着剪切时间的增加呈现出减小的趋势,根据触变性原理,未受剪切前料浆内部颗粒处于相互嵌锁的稳定絮团结构状态,当受到剪切作用时,这种稳定结构被打破,并形成有序流态化,剪切时间越久,稳定结构被破坏得越完全,当达到完全有序流态化时,剪切应力趋于稳定。
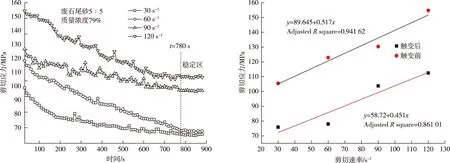
图2 废石尾砂5∶5膏体料浆应力松弛曲线与触变前后参数回归Fig.2 Regression of stress relaxation curves and thixotropic parameters of waste tailings 5∶5 paste slurry
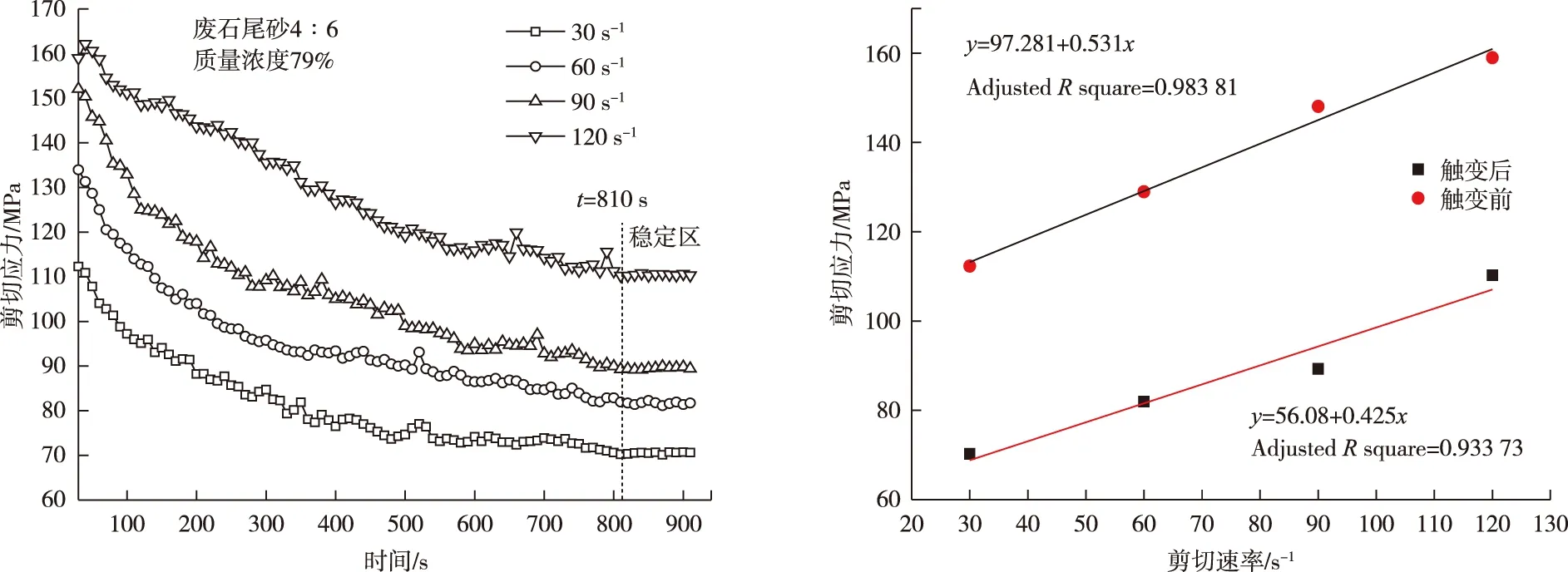
图3 废石尾砂4∶6膏体料浆应力松弛曲线与触变前后参数回归Fig.3 Regression of stress relaxation curves and thixotropic parameters of 4∶6 paste slurry of waste tailings
2 流变参数触变模型的构建
2.1 屈服应力触变规律
在应力松弛曲线平衡时间之前每间隔30 s取一个时间节点,进行回归分析,得到该时刻的屈服应力值,屈服应力随时间的变化曲线如图4所示。
从图4可以看出屈服应力随着触变时间的增加而减小,呈现出负指数函数的增长趋势,减小速率由快到慢,最终趋于稳定,因此,要构建函数关系来表征屈服应力随着时间的变化规律,需满足以下两个条件:
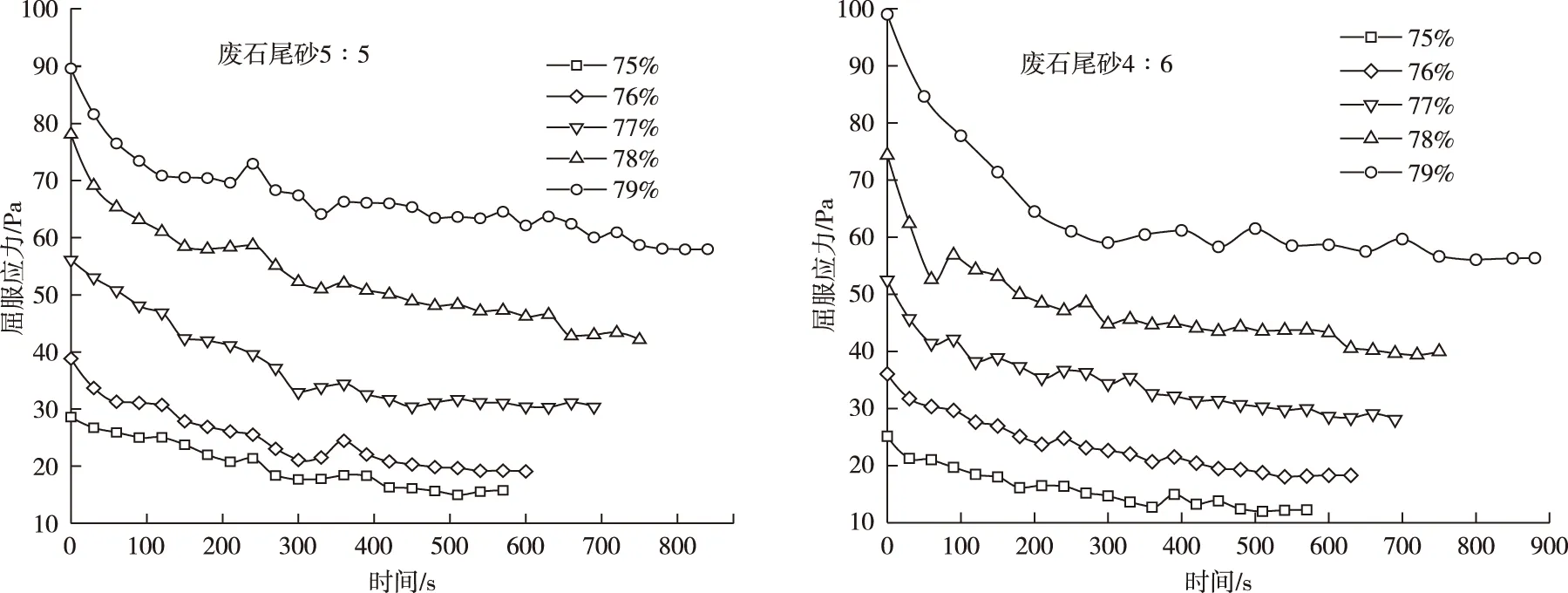
图4 屈服应力随时间变化曲线Fig.4 Yield stress versus time curves
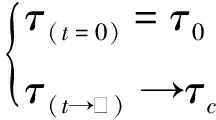
(1)
式中:τ0为触变前屈服用力,Pa;τc为触变后屈服应力,Pa。因此可以构建屈服应力随着时间的变化函数为:
τt=(τ0-τc)·exp(-mt)+τc
(2)
式中:m—时间参数,回归得出;t—触变时间,s。
用式(2)对触变试验结果进行回归分析,求得时间参数m,回归结果如表2所示。

表2 屈服应力-触变时间回归分析结果表
回归曲线如图5所示。
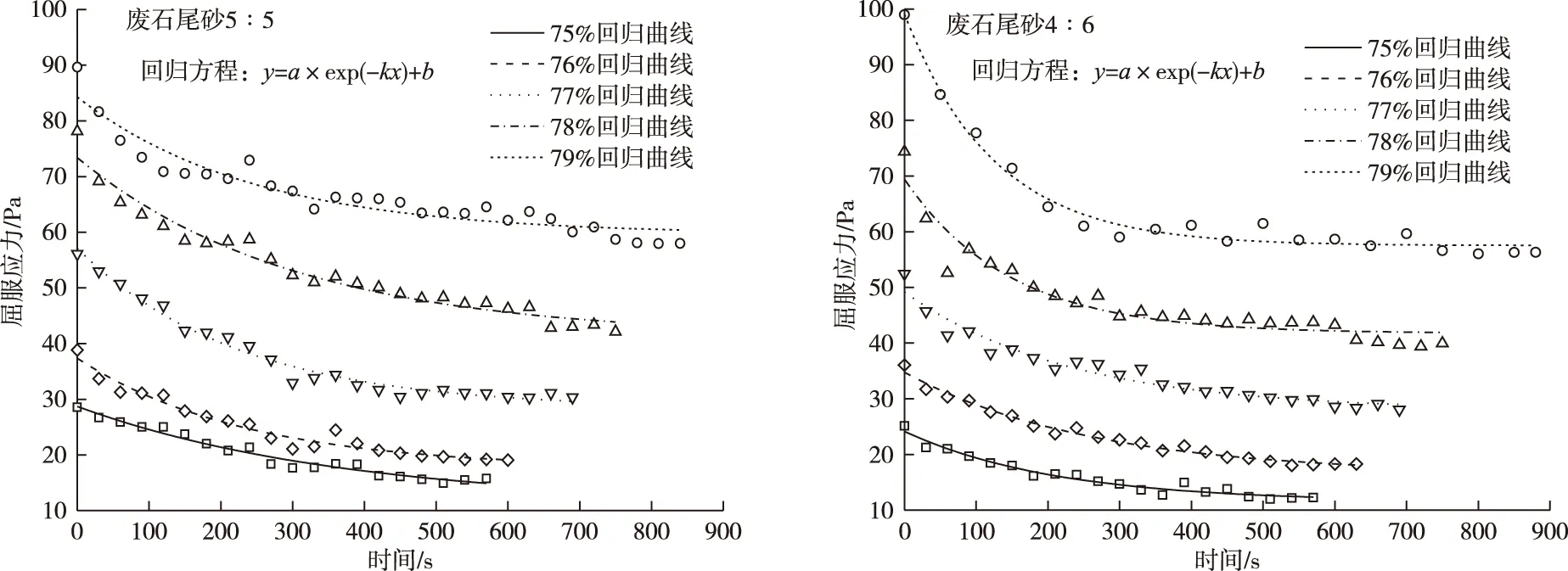
图5 屈服应力-触变时间回归曲线Fig.5 Yield stress thixotropic time regression curves
回归方程如表3所示。

质量浓度/%骨料比(废石∶尾砂)回归参数a回归参数b回归参数m回归方程755∶517.64311.0590.002 98y=17.643exp(-0.002 98x)+11.059765∶519.81117.5540.004 27y=19.811exp(-0.004 27x)+17.554775∶528.79528.2670.004 43y=28.795exp(-0.004 43x)+28.267785∶532.18541.2000.003 32y=32.185exp(-0.004 32x)+41.200795∶524.68759.5670.005 06y=24.687exp(-0.005 06x)+59.567754∶612.69111.4460.004 70y=12.691exp(-0.004 70x)+11.446764∶618.29216.4630.003 85y=18.292exp(-0.004 85x)+16.463774∶621.20627.9190.005 33y=21.206exp(-0.005 33x)+27.919784∶627.68641.7230.006 83y=27.686exp(-0.006 83x)+41.723794∶641.57557.4980.008 02y=41.575exp(-0.008 02x)+57.498
回归参数a的意义为触变前后屈服应力的差值,回归参数b为触变后屈服应力,m为时间参数,其值越大,触变平衡时间越短,屈服应力越容易趋于平衡,m值的大小取决于膏体料浆的配比情况,膏体料浆的配比主要体现在体积浓度与骨料堆积密实度两个方面,因此,可以用膏体料浆的固体填充率Cv/φ来表征时间参数m值的大小,固体填充率与时间参数m的关系如图6所示。
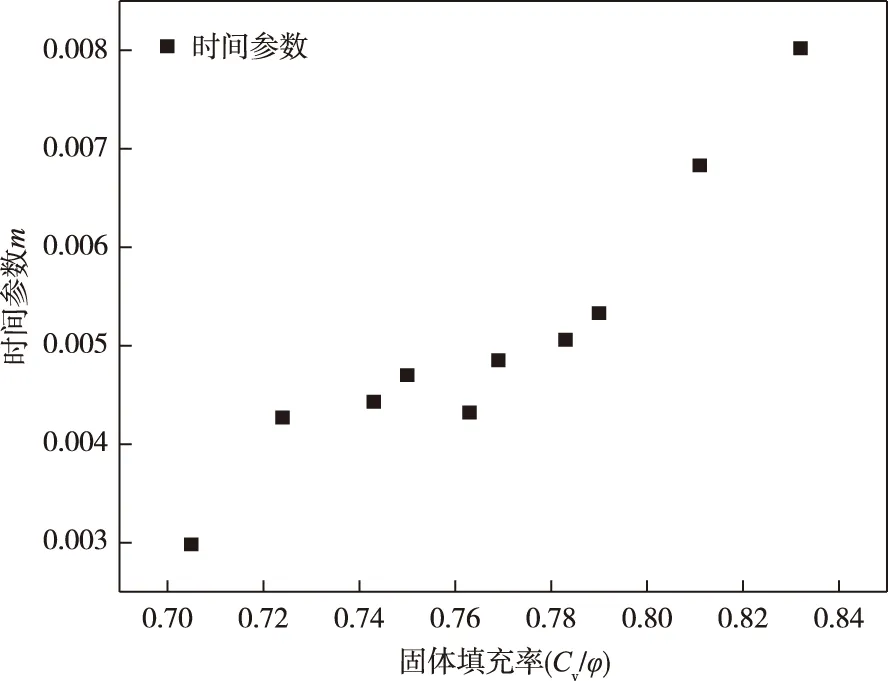
图6 时间参数-固体填充率关系散点图Fig.6 Scatter plot of the relationship between time parameters and solid filling rate
从图6可以看出,时间参数m和固体填充率之间满足线性关系,因此可以构建时间参数与膏体料浆固体填充率的关系函数,见式(3)。
(3)
拟合曲线如图7所示。

图7 时间参数-固体填充率拟合曲线Fig.7 Fitting curve of time parameter and solid filling rate
回归方差分析见表4。

表4 时间参数-固体填充率回归方差分析
方差分析显示:F=505.265 66>F0.995(3,27)=5.36>F0.99(3,27)=4.6,属高度显著。
2.2 屈服应力触变平衡时间
为了估算屈服应力触变平衡时间,可以通过近似斜率法来实现对屈服应力触变平衡时间的估算,对式(2)进行求导,得出屈服应力-时间曲线斜率的表达式见式(4)。
(4)
求式(4)的反函数,得式(5)。
(5)
式中:τ0—触变前屈服应力,Pa;τc—触变后屈服应力,Pa;m—时间参数;t—触变时间,s。
由于屈服应力-时间的曲线是无限趋近于水平的曲线,因此定义不同精度的斜率值,求得的屈服应力触变平衡时间也不同,所得触变平衡时间表达式见式(6)。
(6)
式中:tk—不同精度的触变时间,s。
令k=-10-2时,求得屈服应力触变平衡时间如表5所示。
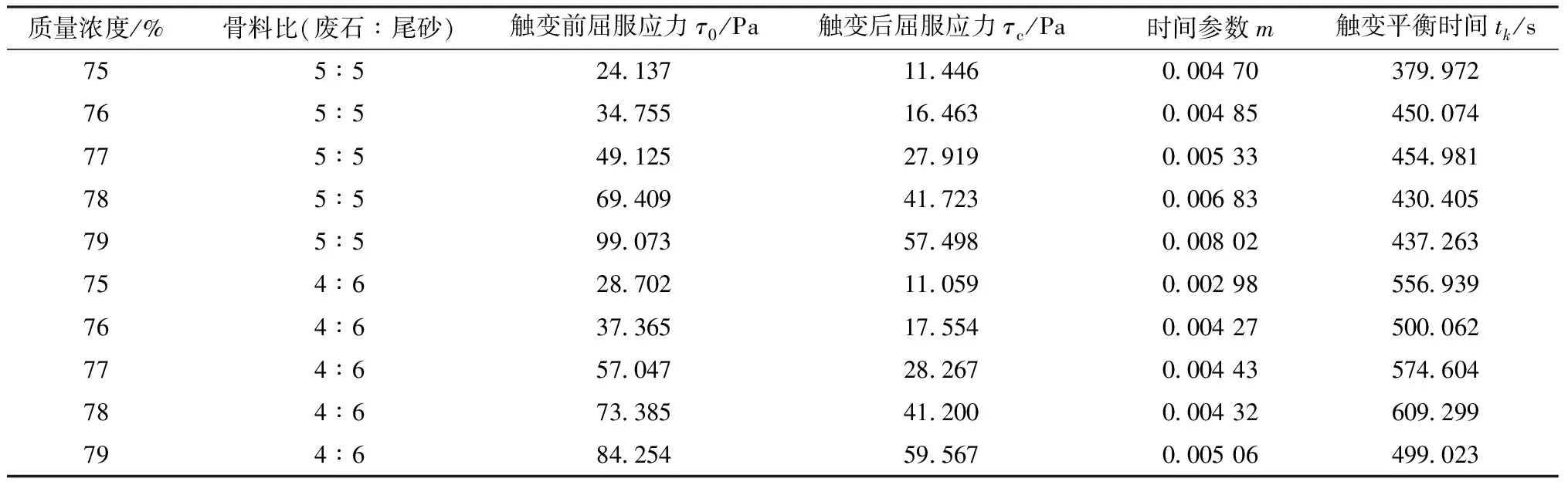
表5 屈服应力触变平衡时间计算结果
3 结论
1)通过膏体料浆的应力松弛试验可知,膏体料浆的剪切应力随着剪切时间的增加呈现出减小的趋势,当剪切时间足够大时,剪切应力趋于稳定。
2)膏体料浆屈服应力随着触变时间的增加而减小,呈现出负指数函数的增长趋势,减小速率由快到慢,最终趋于稳定,并构建了膏体料浆屈服应力触变模型。
3)构建了膏体料浆屈服应力触变平衡时间估算公式。
