路基高边坡稳定性分析及防护措施研究

摘要：边坡稳定性是影响公路工程建设、运营安全的关键因素，尤其是路基高边坡，受力变形机制复杂，施工难度大，需要对其稳定性及防护措施格外重视。文章以某山区高速公路为研究对象，采用有限元软件Midas/GTS建立三维模型，分析强降雨前后路基边坡稳定性，得出结论为：破坏机制复杂的边坡宜采用简化Bishop和数值分析法综合评估其稳定性;边坡安全系数会随着降雨历时和降雨强度的增加而不断降低;预应力锚索的锚固力可将滑坡推力传递到更深的稳定地层中;高边坡安全系数会随着锚杆长度的增加而提高，但超过某一临界值，稳定性增加幅度不大。

关键词：路基边坡;稳定性;降雨入渗;防护措施;有限元模型

文献标识码：U416.1+4-A-03-008-4

0 引言

随着我国交通网络地不断完善，公路工程作为推动当地经济发展的重要设施，其建设规模日益扩大。而边坡稳定性是影响公路工程建设、运营安全的关键因素，如果边坡防护措施选择不当，有可能引起严重的经济损失和人员伤亡[1]，尤其是路基高边坡，受力变形机制复杂，施工难度大，需要对其稳定性及防护措施格外重视。目前国内学者及工程技术人员也针对公路高边坡展开了部分研究，如贾鹏云[2]以顺层岩质高边坡为研究对象，分别利用有限元软件GEO-SLOPE、ANSYS对其安全系数进行计算，并得到潜在滑动面的发展趋势;罗元斌[3]依托某岩质边坡，利用三维计算方法，研究了粘聚力、内摩擦角、降雨强度等参数对边坡稳定性的影响，并计算出边坡最大水平位移、应力等参数;张韬[4]运用岩体质量分类法对10 d高速沿线高陡岩质边坡破坏特征进行了调查，提出了相应的防护措施，利用离散元软件UDEC计算出降雨对高边坡安全系数的影响规律。因此，对路基高边坡稳定性的分析及防护措施研究具有十分重要的工程意义。

1 公路高边坡稳定性计算方法

对于公路高边坡安全系数计算，《公路路基设计规范》（JTG D30-2015）的3.7.5条要求规模较大的碎裂结构岩体边坡或土质边坡宜采用简化Bishop，如边坡破坏机制复杂，宜结合数值分析法进行分析，以合理评估高边坡的稳定性。

1.1 简化Bishop法

1.1.1 均质土边坡

简化Bishop法模型简单，计算精度高，是均质土边坡稳定性计算中最常用的一种刚体极限平衡法[5]。该方法是将滑坡体划分成n个宽度相同的垂直条块（图1），假设各条块间只存在水平条间力，竖向条间力等于0且滑体力矩平衡，同时，以滑动圆弧的圆心为力矩中心点，计算得到抗滑力矩与下滑力矩的比值即为边坡安全系数，计算公式如下：

Ti=∑ni=1[（Wi-uibi）tanφi+cibi]/mαi∑ni=1Wisinαi （1）

式中：Wi——第i条条块的重力（kPa）;

bi——第i条条块的宽度（m）;

ci——滑面粘聚力（kPa）;

φi——滑面内摩擦角（°）;

αi——圆弧底面倾角（°）;

ui——孔隙水压力（kPa）。

1.1.2 岩质边坡和非均质土边坡

岩质边坡和非均质土边坡的滑动面一般不是圆弧形，计算其安全系数时不宜直接采用简化Bishop法。笔者在简化Bishop法基本假设的基础上，利用积分中值定理、摩尔库伦理论等推导出了能计算各种形式滑动面的扩展Bishop法。该方法能与传统的简化Bishop法兼容，且无须计算力矩，简化了边坡安全系数分析难度，计算公式如下：

Fs=∫lτfdl∫lτdl=∑Nitanφi+ciliWisinαi （2）

式中：Ni——第i条条块底部法向力（kPa）;

Ni——第i条条块底部长度（m）。

1.2 数值分析法

随着计算机技术的飞速发展，数值计算法在岩土计算领域的应用日益普遍，一般包括有限元法、有限差分法、离散元法等，其中有限元法的应用最广泛。有限元法用于分析边坡稳定性时，能将其安全系数与滑动面位移、应力、塑性区等联系起来，能更好地分析路基高边坡失稳变形机制。其关键是判断边坡临界破坏状态，主要判据有两种[6]：（1）邊坡模型节点最大水平位移达到某值;（2）迭代计算不收敛。

2 公路高边坡稳定性计算模型的建立

2.1 工程实例

以某山区高速公路为研究对象，采用有限元软件Midas/GTS建立三维模型来分析强降雨前后路基边坡稳定性。该高速公路全长28.6 km，起讫桩号为K10+285～K38+885，地质条件较复杂，地下水位低，沿线出现了大量高边坡。边坡计算断面选择桩号为K15+686，边坡最大高度为34.6 m，分四级进行开挖，每级边坡控制坡高为10 m，第一级和第二级边坡坡比为1∶1.1，第三级和第四级边坡坡比为1∶1.25，各平台宽均为2 m，如图2所示。

根据区域地质资料，场区处于相对较稳定的地质环境，未发现活动性深大断裂，地震基本烈度为Ⅵ度。同时，场区内地层分布较连续，无地震作用下的可液化地层，场地土属中硬土，场地类别为Ⅱ类。根据设计资料及相关岩土试验可知，该高边坡岩土体分为两层，从上至下分别为强风化板岩和中风化板岩，岩体的物理力学指标建议值如表1所示。

2.2 路基高边坡有限元模型

2.2.1 软件介绍

Midas/GTS是由韩国开发的一款通用岩土有限元分析软件，操作界面简单，内置多种本构模型，能计算边坡稳定性、流固耦合、动力响应等，并输出滑动面的位移、应力、应变等。Midas/GTS计算边坡安全系数步骤如下：CAD建立模型→Midas导入DWG文件→交叉分割模型→定义材料及属性→2D网格划分→添加约束条件→初始地应力平衡→强度折减法计算边坡稳定性→结果后处理。

2.2.2 模型基本假设

在利用Midas/GTS计算公路边坡安全系数时采用的本构关系是摩尔-库伦屈服准则，并作以下假设[7]：（1）根据对称性原则，模型取半幅路基边坡;（2）高边坡底部对X方向、Y方向、Z方向完全约束，坡面和坡顶为自由边界;（3）地下水位较低，忽略其影响;（4）锚索和土体之间的接触面选择Interface Element接触单元来模拟。

2.2.3 网格划分及边界条件

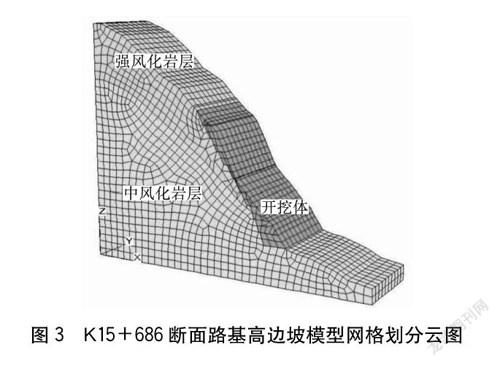
根据相关研究成果，网格尺寸、网格数量对模型计算结果和计算效率影响较大。在综合考虑边坡安全系数计算精度和计算机运算速度的基础上，利用Midas/GTS的二维实体单位（六节点四面体）对边坡坡体进行网格划分。其中边坡坡面2 m范围内网格进行加密处理，网格控制尺寸取1 m，其他部位网格尺寸取2 m，共划分出4 251个单元，6 342个节点。边坡网格划分情况如图3所示。

3 公路高边坡安全系数计算结果

在确定计算参数、建模、划分网格、设置边界条件等工作完成之后，对路基边坡稳定性开展验算。边坡稳定性计算考虑了正常工况和非正常工况，其中前者是边坡处于天然状态，后者是边坡处于暴雨或连续降雨状态。

3.1 正常工况

路基边坡在未采取防护措施的工况下，Midas/GTS软件计算出的边坡安全系数为1.12，最大水平位移发生在坡脚附近，达到了22.8 mm。同时，边坡坡体出现了贯通的连续滑动面，存在坡体沿软弱结构面向下滑移的可能性。

3.2 非正常工况

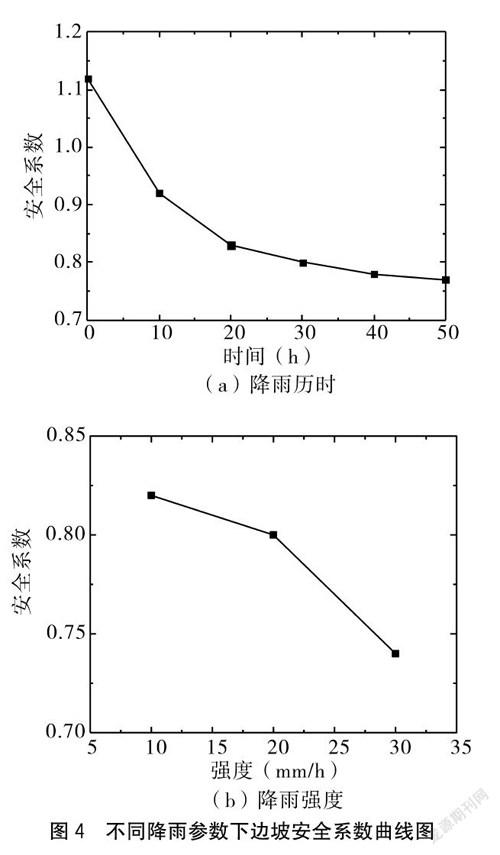
降雨入渗会引起边坡土体的含水率提高，而含水率的增加又会改变土体的孔隙压力、抗剪强度、重度等参数，进而降低边坡的稳定性。为了深入研究降雨对路基高边坡稳定性的影响规律，笔者利用Midas/GTS的渗流模块进行了多次的迭代计算，得到了不同降雨历时和降雨强度下边坡安全系数（见图4）。

由图4可知，随着降雨历时的增加，边坡安全系数不断减小，边坡稳定性不断降低。在降雨初期，边坡的安全系数为1.12。当降雨历时达到20 h，其安全系数陡降了19.6%，此时边坡已经处于不稳定状态。当降雨历时超过20 h，边坡安全系数的降低速率逐渐减缓，直到失稳破坏。

在相同的降雨时间下，边坡的安全系数随着降雨强度的增加而减小，且降雨强度越大，其安全系数的降低速率越快。出现这种现象的主要原因在于：当降雨强度较大时，渗入边坡内部的雨水量越多，使得坡体的负孔隙水压力减小较快，从而导致边坡安全系数降低较快。

4 公路高边坡安全系数防护措施及效果评价

高边坡正常工况和非正常工况下安全系数均小于《公路路基设计规范》（JTG D30-2015）的规定值1.2，且边坡危险滑动面位于边坡表层，拟采用预应力錨索对其加固处理。

4.1 边坡锚固机理

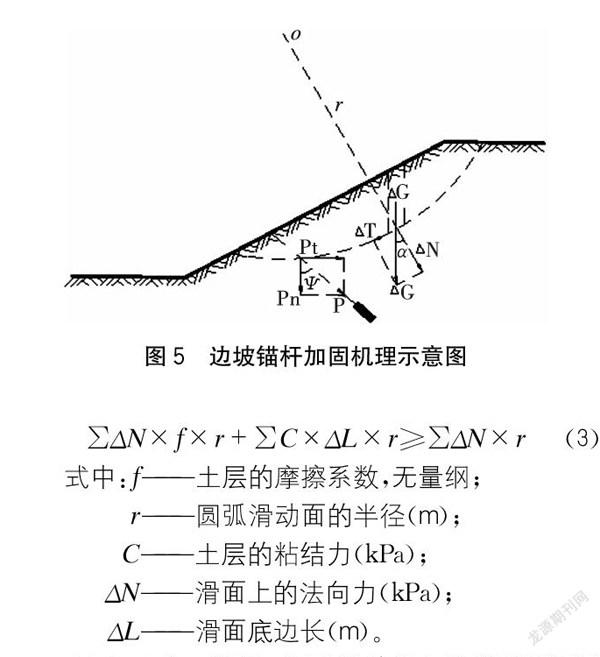
预应力锚杆索加固技术可以充分发挥岩土体本身强度和潜力，控制工程变形，几乎是解决公路高边坡失稳破坏最经济有效的措施之一。路基边坡往往受到潜在滑动面以上岩土体切向力、渗透水及其他荷载的作用导致失稳，而其稳定性主要是由边坡可能滑动面岩土体的抗剪强度参数来维持。为了避免边坡失稳破坏，预应力锚索的锚固力（视为作用在滑面的集中力）必须能使作用在滑动面上的所有力系保持平衡，即抗滑力矩大于下滑力矩，加固原理如图5所示。

∑ΔN×f×r+∑C×ΔL×r≥∑ΔN×r （3）

式中：f——土层的摩擦系数，无量纲;

r——圆弧滑动面的半径（m）;

C——土层的粘结力（kPa）;

ΔN——滑面上的法向力（kPa）;

ΔL——滑面底边长（m）。

由图5可知，锚索可以将滑坡推力传递到更深的稳定地层中，利用稳定地层的锚固作用和被动抗力，使得边坡保持稳定状态。锚索阻止滑坡体下滑的作用主要源于潜在滑动面上锚索与岩土体的相互作用，此时锚索可视作一个约束点，每个约束点均可提供正压力和上提力，前者可以阻止滑坡体与稳定岩土体分离，后者可以阻止滑坡体的下滑。当这些约束点的数目、位置和强度布置合理时，才能够充分发挥锚索的锚固作用，使边坡保持稳定状态[8]。

4.2 锚索长度对边坡稳定性的影响

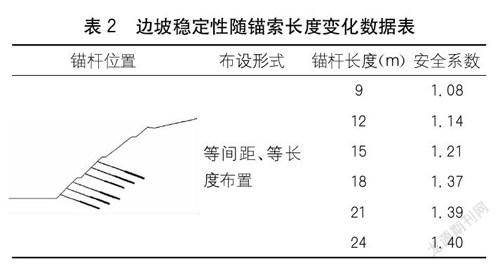
遵循“强脚固腰”的原则，选择预应力锚索对一级和二级边坡加固，锚索的竖向间距为3 m，锚索倾角为20°，锚固段长度取8 m。取不同锚杆长度进行多次试算，得到了不同锚索长度下边坡的安全系数如表2所示。

计算结果表明，高边坡安全系数随着锚杆长度的增加不断提高，但增长速率逐渐变缓。即当预应力锚索长度<15 m时，边坡安全系数与锚索长度基本呈线性正相关，提高速率较快;当预应力锚索长度>15 m时，边坡稳定性增长幅度不大。锚索加固长度24 m相对于18 m而言，防护工程造价大幅增加，但边坡的安全系数仅仅提高了2.2%，可以忽略不计。因此锚索最佳设计长度为18 m，此时高边坡的安全系数达到了1.37，满足路基设计规范要求。

4.3 边坡锚索前后水平位移变化

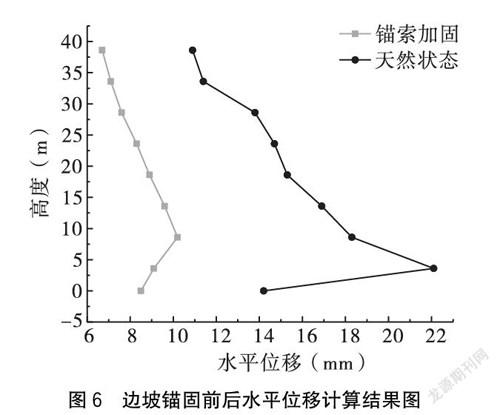
预应力锚索最佳锚固长度确定后，Midas/GTS计算出的高边坡锚固前后水平位移如图6所示。

由图6可知，边坡在未加固时，其水平位移发生在坡脚，最大值达到22.8 mm。边坡采取预应力锚索加固后，其水平位移最大值仅为9.1 mm，水平位移降低率达到60.1%，且整个坡面的变形比较连续，潜在滑动面向内扩展，基本不存在坡体沿软弱结构面向下滑移的可能性。

5 结语

本文根据公路高边坡的稳定性分析方法特点，并利用Midas/GTS软件分析了边坡降雨和锚索加固前后的安全系数变化规律，得到以下几个方面的结论：

（1）破坏机制复杂的边坡宜采用简化Bishop和数值分析法综合评估其稳定性，并选择合适判据确定边坡临界破坏状态。

（2）雨水会使边坡内部负孔隙水压力和抗剪强度减小，容重增加，导致边坡安全系数会随着降雨历时和降雨强度的增加而不断降低。

（3）预应力锚索的锚固力可视为作用在滑面的集中力，给边坡滑体提供正压力和上提力，并将滑坡推力传递到更深的稳定地层中。

（4）高边坡安全系数会随着锚杆长度的增加而提高，但超过某一临界值，稳定性增加幅度不大。同时，边坡锚固后使坡面变形连续，降低坡体水平位移。

参考文献

[1]格桑顿珠.公路边坡稳定性分析及处治技术优化设计研究[D].重庆：重庆交通大学，2012.

[2]贾鹏云.顺层岩质高边坡稳定性分析及处治方案研究[J].山西交通科技，2017（4）：29-32.

[3]罗元斌.边坡工程稳定性分析及处治技术研究[D].长沙：中南大学，2006.

[4]张 韬.十天高速典型千枚岩高边坡稳定性分析与支护设计优化[D].西安：长安大学，2013.

[5]乔 翔.基于极限平衡法的高边坡稳定性分析及处治措施[J].铁道建筑，2017，57（8）：89-93.

[6]黄生文，何 韬，冯 宇.岩土质混合高边坡稳定性分析与处治建议[J].长沙理工大学学报（自然科学版），2012，9（1）：46-53.

[7]郭秋根.不同处治方法的边坡稳定性数值模拟[D].赣州：江西理工大学，2012.

[8]王 亮，郭 昕，冯小丽，等.永龙高速公路ZK56+860～ZK56+940边坡稳定性分析及处治效果评价[J].公路工程，2016，41（2）：166-168，177.

收稿日期：2021-03-18

作者简介：农明科（1989—），工程师，主要从事路桥施工工作。