内压条件下轴向内表面裂纹管道蠕变断裂参量C*的工程估算方法

刘长军，蔡 君，孙春燕，谈建平，邵雪娇

(1.华东理工大学机械与动力工程学院，承压系统与安全教育部重点实验室，上海 200237；2.中国核动力研究设计院，核反应堆系统设计技术重点实验室，成都 610213)

0 引 言

为描述含缺陷构件的蠕变裂纹扩展性能，学者们提出了多种蠕变断裂参量，其中参量C*与蠕变裂纹扩展速率的关联效果最好，使用最广泛[1]，并且已被多种标准和规范采纳[2]。目前，计算C*参量的方法主要包括有限元法、实验室半经验法，以及工程上应用的参考应力法和类比美国电力研究协会(EPRI)J积分工程估算法的C*估算法。其中：有限元法的计算准确度较好，但标准化难度大，对使用人员要求高，耗时长，因此其工程应用受限；实验室半经验法在计算C*参量时需要测定加载位移(或裂纹张开位移)，而工程构件获取该参数的难度大，因此其工程应用受限；参考应力法虽然是工程上普遍采用的计算方法，但是其计算精度与极限载荷的确定相关，通常计算结果比有限元结果高2～3倍及以上，有时也会出现低估的情况[3-5]。鉴于材料的稳态蠕变本构与塑性本构关系具有类比性，LANDES等[6]将弹塑性断裂参量J积分类比至大范围蠕变条件下的蠕变断裂参量C*来表征稳态蠕变裂纹扩展行为。因此，同样可类比推导EPRI-J积分估算方法得到C*估算法[7-11]。该C*估算法并非由EPRI直接提出，但为了便于文中讨论，将其简称为EPRI-C*估算法。EPRI-C*估算法一般根据裂纹尺寸a/t、a/c，管道尺寸Ri/t(a，c，t分别为裂纹深度、裂纹半长和管道壁厚，2Ri为管道内径)和蠕变指数n，查询EPRI手册得到对应的J积分全塑性解h1(简称塑性解h1)，将h1值代入方程计算得到C*值；这种方式简化了工程人员的操作，其核心在于塑性解h1值的确定[3]。但是该数值与材料、几何结构、裂纹尺寸等参数相关，按照这些相关参数编写的塑性解表格复杂，查询不便。

综上，现有C*参量的工程估算法无法兼顾结果准确度与操作简便性。为此，作者基于EPRI-C*工程估算法中Zahoor的C*估算方法[10]，通过引入x0系数与塑性解h1构成与蠕变指数n无关的函数，建立了一种改进的C*参量计算方法；应用该方法计算得到不同蠕变指数(n=3，5，7，9)、不同裂纹尺寸(a/c为1/3，a/t分别为0.2，0.4，0.6)的轴向内表面裂纹管道(Ri/t=10)在内压下的蠕变断裂参量C*值，并与有限元方法、参考应力法中的R6整体解和Kim优化解计算的C*值进行对比，用以验证改进方法计算结果的准确度。

1 蠕变断裂参量C*的工程估算方法

1.1 现有EPRI-C*工程估算法

对于内压条件下内表面含轴向裂纹的管道，Kumar等最先给出了相应的塑性J积分的估算公式[12]，以此为理论基础发展出了相应的C*估算公式，目前常见的有Kumar-Yoon估算公式[8]、Kumar-EPRI估算公式[7]、Zahoor估算公式[10]和Yagawa估算公式[11]。表1总结了上述4种形式的EPRI-C*工程估算法计算管道裂纹C*值的适用对象、范围、优缺点与结果准确度排序。采用EPRI-C*工程估算法计算蠕变断裂参量不需要工程人员掌握太多理论知识，只需查询EPRI手册获取塑性解h1的值，代入估算公式计算C*值即可。但是塑性解h1的影响因素较多，包括Ri/t，a/c，a/t和n，并且利用不可压缩性有限元计算推导此类h1的过程比较繁琐。通常由此类h1值计算得到的C*值远高于实际值[12]，保守性较高。

表1 现有EPRI-C*工程估算法的对比Table 1 Comparison of current EPRI-C* engineering estimation methods

1.2 方法改进

利用EPRI-C*工程估算法计算内压条件下轴向裂纹管道C*值时，Zahoor估算公式所得解的准确度优于其他EPRI-C*工程估算法所得解的准确度[3]。因此，作者基于Zahoor估算公式的理论进行估算方法改进。

Zahoor塑性J积分计算公式[10]如下：

Jp=ασ0ε0t·h1(a/t,a/c,n,Ri/t)·(σ/σ0)n+1

(1)

式中：Jp为塑性J积分；α为与材料相关的常数；σ0为屈服强度；ε0为与σ0对应的应变；σ为任意时刻垂直于裂纹方向的应力。

基于此塑性J积分将EPRI-J积分推广到C*的估算，C*的计算公式为

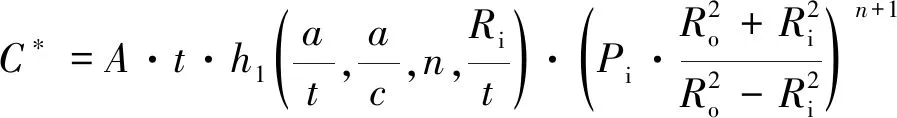
(2)

式中：A为Norton方程系数；Pi为管道内压；2Ro为管道外径。

(3)

对式(3)两边取对数，得

lnh1=nlnσ0+(lnC+lnσ0)

(4)

式(4)中lnC+lnσ0和lnσ0仍为常数，可分别记作A1与B，则式(4)可改写为

lnh1=A1+Bn

(5)

由式(5)可以看出，lnh1与n成线性关系，其中B为直线的斜率；孙亮等[13]在其研究中已经证明了该关系的准确性。h1与n相关，因此作者尝试寻找一个系数x，使得h1(n)·xn+1成为一个与n无关的函数。对该函数取对数，并代入式(5)，简单计算后得到的公式如下：

ln[h1(n)·xn+1]=(B+lnx)n+A1+lnx

(6)

(7)

2 有限元计算方法

选取内压条件下含内表面半椭圆形轴向裂纹的管道为研究对象，通过ABAQUS有限元软件建立模型，计算蠕变指数分别为3，5，7，9，a/c为1/3，a/t分别为0.2，0.4，0.6时对应的蠕变断裂参量C*值，用于检验改进的EPRI工程估算法的准确性。

2.1 材料模型

有限元材料模型使用的是弹性-幂率蠕变模型，蠕变本构方程为

(8)

材料参数选自文献[14]，如表2所示；表中ν为泊松比。

表2 管道模型相关的材料参数Table 2 Material parameters for pipe model

2.2 几何模型

选择较常见的管道进行研究，其内半径Ri为380 mm，外半径Ro为418 mm，壁厚t为38 mm，长度L为1 140 mm，管道内表面裂纹为半椭圆形，如图1所示。裂纹尺寸以a/t和a/c表示，a/c均取1/3，a/t分别取0.2，0.4，0.6。考虑到管道模型的对称性，采用管道的1/4进行有限元建模，模型如图2所示。该有限元模型使用C3D8单元进行网格划分，并且通过了网格无关性验证与正确性验证。裂纹尖端积分路径一共设置8条，其中C*取后6条积分路径的平均值。

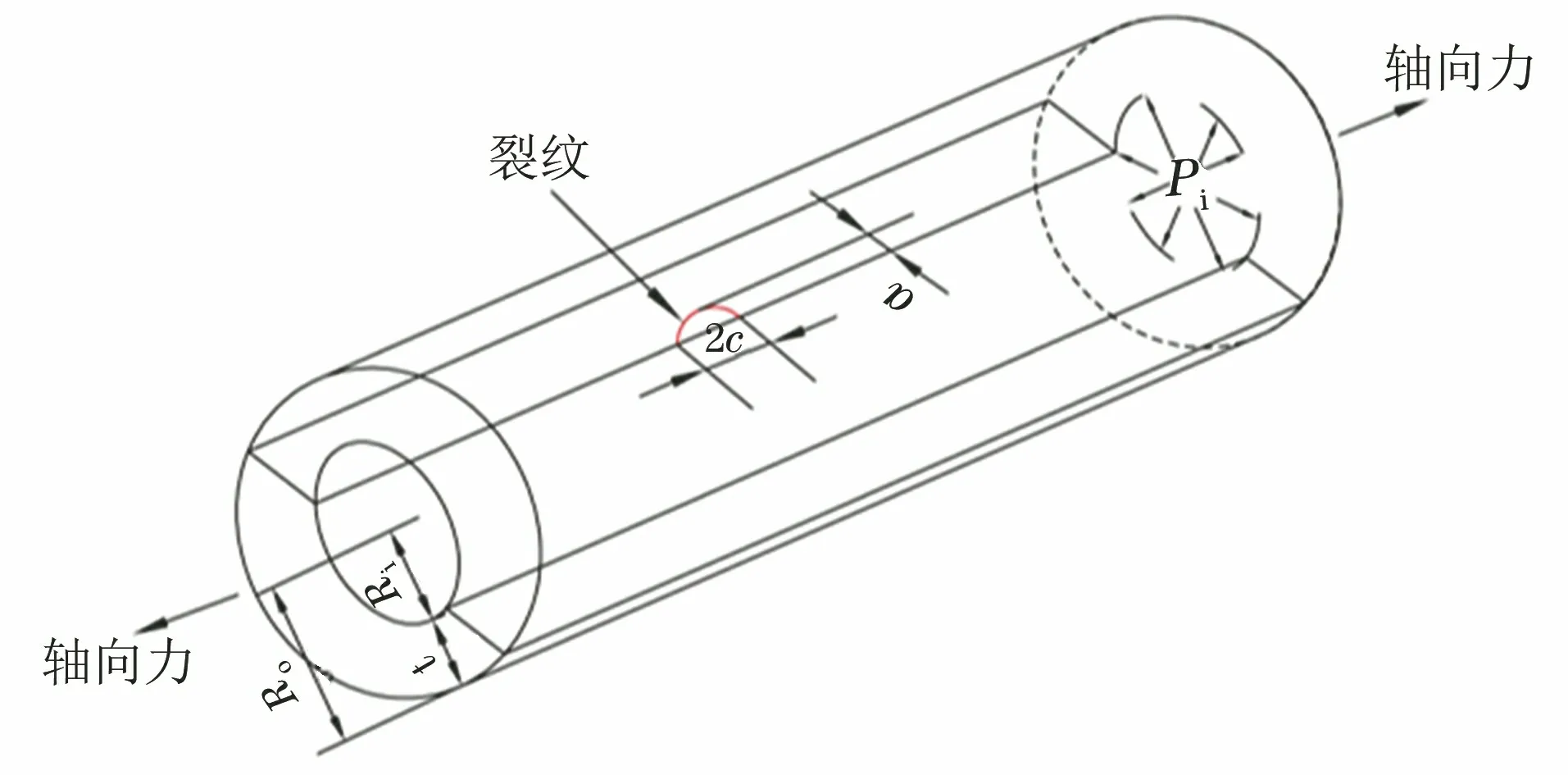
图1 内表面半椭圆轴向裂纹示意Fig.1 Diagram of semi-elliptical axial crack on inner surface

图2 轴向裂纹管道有限元模型Fig.2 Finite element model for pipeline with axial crack:(a)whole model and (b)enlargement at crack tip

2.3 载荷及边界条件

为模拟管道实际情况，需对模型施加对应的载荷与边界条件。在管道内表面及裂纹面上施加大小为6.2 MPa的内压，在远离裂纹的管道横截面上施加内压对应的轴向力，经圆筒轴向力公式[15]计算得到的轴向应力为31 MPa。在管道轴向面上施加周向对称约束，在裂纹端的横截面上施加轴向对称约束。

3 改进方法计算结果的准确度验证

在EPRI-C*工程估算法中，Zahoor估算公式的准确度优于其他估算公式的准确度，因此仅将改进方法与Zahoor估算公式进行比对。而在参考应力法中，R6整体解与Kim优化解准确度较高[12]，R6局部解在不同裂纹尺寸a/t下的差异较大[3,12]，因此仅将改进方法与R6整体解和Kim优化解进行对比。

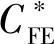
表3 不同裂纹尺寸下的和x0Table and x0 of different crack size

图3 不同裂纹尺寸和不同n值下改进方法、Zahoor估算公式、R6整体解、Kim优化解与有限元法所得C*值的比值Fig.3 Ratios of C* results obtained by improved solution,Zahoor solution,R6 global solution and Kim solution to those obtained by finite element solution under different crack size and different n values

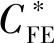
4 结 论

(2)参考应力法中的R6整体解与Kim优化解所得的C*值比有限元方法所得C*值高2～8倍，且随着裂纹尺寸a/t和蠕变指数n增大，参考应力法的计算误差增大。

(3)改进方法所得C*值与有限元法方法所得C*值的比值始终保持在1左右，计算结果准确度高；相比于Zahoor估算公式，改进方法在蠕变指数n为3时的计算准确度略有改进，但随着n增大2种方法的计算准确度趋于相同。