计入配合精度影响的风电主轴轴承特性与寿命

任 禄，王建梅，宁文钢，杨 晋，侯定邦

(1.太原科技大学 重型机械教育部工程研究中心，山西 太原 030024；2.太原重工股份有限公司技术中心，山西 太原 030024)

0 前言

全球气候变化是21世纪人类面临的重大挑战。可再生能源的发展已成为主流，其中风力发电成为实现碳中和目标的主力。风力发电机组主轴轴承工作条件恶劣，可靠性要求严格但故障占比较高[1]。因此，对主轴轴承的受载特性及疲劳寿命分析提出了更高的要求。

肖文等[2]通过建立风电主轴双列圆锥滚子轴承的全尺寸接触模型，研究了给定工况下风电主轴轴承承载接触机理。杜静等[3]使用Gap单元模拟轴承滚子，得到了轴承整体的接触应力分布。郑景阳等[4]提出了一个综合的准静态模型，考虑角不对中、外载荷和摩擦力等因素以研究风电双列圆锥滚子轴承的内载荷和接触压力分布。徐四宁等[5]通过建立给定特征工况的风电主轴调心滚子轴承滚子与滚道的接触模型，分析了载荷比对滚子姿态接触角的影响。刘静等[6]基于非理想Hertz线接触特性，研究了位移激励形式和局部故障尺寸对圆柱滚子轴承振动特性的影响规律。朱亮等[7]应用典型的联合载荷和边界条件，对各种不同接触角的轴承模型进行疲劳寿命分析，得出了轴承承载过程中的疲劳安全因子、疲劳寿命的相互关系。李云峰等[8]对风力发电机组轴承疲劳寿命的计算方法进行研究，更加准确的计算风电轴承寿命。王佳伟等[10]基于RomaxDesigner仿真分析了轴承径向游隙与润滑对风机低速输入轴轴承疲劳寿命的影响。褚景春等[11]对风电机组用双列调心滚子轴承结构进行改进，有效缓解了偏载问题。王洪波等[13-14]详细阐述了风电机组主轴及轴承座装置的装配工艺，介绍了特定轴承加热工艺参数的确定及轴向间隙的控制方法，有效控制其装配质量。郭铁能等[15]建立了考虑内圈离心膨胀和热位移的轴承过盈配合模型，结合Harries轴承动力学模型，进行了轴承配合过盈量对主轴动力学特性影响分析。王建梅等[16-19]基于厚壁圆筒理论对过盈联接深入研究，构建了过盈配合下各配合面接触压力和过盈量的计算公式及不同游隙轴承应力和轴心轨迹数值计算的算法。王晓强等人[20]基于Deform建立风电轴承材料42CrMo工件的超声滚挤压过程数值模拟模型，研究工艺参数对工件表面粗糙度的影响，设计实验并对其进行参数优化。

上述文献从承载、结构、工艺以及材料方面做了大量工作，然而对主轴系统组件在设计过程中轴承与周边结构之间的影响程度考虑较少。本文以某兆瓦风电机组主轴圆柱滚子轴承为研究对象，通过考虑计入轴承安装尺寸精度、和周边结构安装的影响，分析轴承不同配合精度时的力学性能以及对轴承寿命的影响，从而保证轴承装配过程中的安装精度，提高轴承的性能和使用寿命。

1 轴承载荷分布及寿命计算

1.1 轴承滚动体接触载荷计算

风力发电机主轴属于低速轴，主轴承转速较低，因而轴承滚子和内外圈所产生的离心力和陀螺力矩可以忽略不计。对于给定的滚子-滚道接触，载荷与变形关系的一般式[21]可表达为

Q=Knδn

(1)

式中,对球轴承，n=1.5；对滚子轴承，n=10/9；Q滚子所受载荷；Kn为载荷位移常数；δ为位移或接触变形。

对于刚性支承的轴承，径向载荷下任意角度位置的滚子径向位移为

(2)

式中，δr是θ=0处套圈的径向位移，Δ为轴承径向游隙。存在游隙的向心轴承位移如图1所示。

图1 向心轴承位移图

任意角位置滚动体最大变形量为

(3)

其中，

(4)

根据载荷与变形的关系，可得任意角位置接触载荷为

(5)

为满足静力平衡，作用的径向载荷必须等于滚动体载荷的竖向分量之和，即

(6)

1.2 过盈配合下轴承内部的载荷分布

轴承通常采用内圈或外圈带过盈量安装，但过盈量会引起内、外圈胀缩，不仅会引起轴承内圈周向应力的改变，同时也会造成游隙变化。轴承在承受一定载荷进行旋转时，由于载荷作用，轴承内、外圈及滚动体之间同时会发生弹性位移，从而引起轴承游隙的变化并导致轴承内部最大载荷及载荷分布的变化，影响轴承寿命。

如图2a所示，外圆环的外径为D1，内径为Ds的轴承内圈，对于空心轴与轴承内圈制造材料相同或相差不大的情况下，由于压配合引起的D1增加量为

(7)

如图2b所示，内圆环是外径为Dh，内径为D2的轴承外圈，对于轴承座与轴承外圈制造材料相同或相差不大的情况下，则由于压配合引起的D2的缩小量为

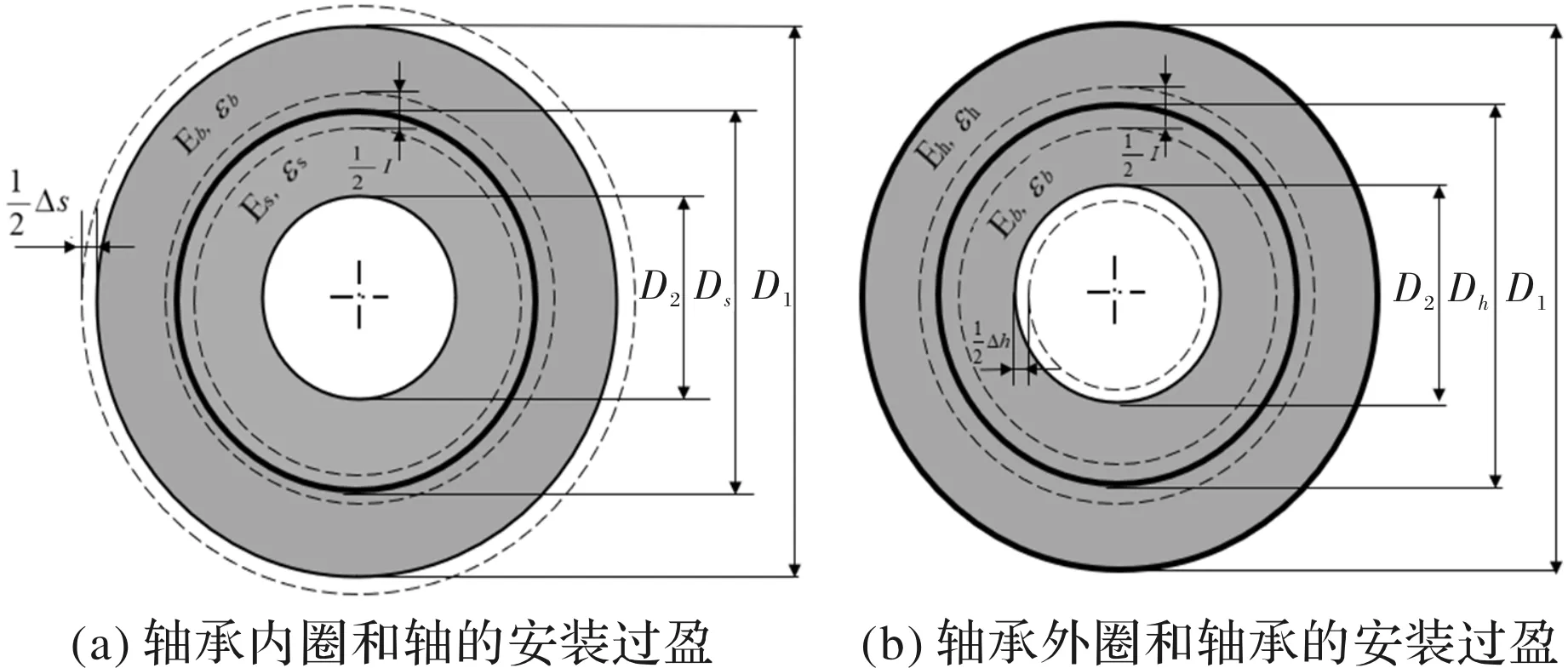
图2 轴承装配过盈示意图

(8)

通过过盈配合安装的轴承在内圈和外圈滚道都产生了变形，从而对轴承的初始游隙产生影响。由游隙改变量，利用轴承滚动体接触载荷计算公式即可求得轴承修正的载荷分布。轴承过盈装配产生的游隙变化量ΔC等于过盈配合产生的内圈滚道变形量Δs和外圈滚道变形量Δh之和[24]，即

ΔC=-Δs-Δh

(9)

1.3 轴承寿命计算

风电机组国际标准对主轴轴承的疲劳载荷下的寿命计算标准分别为ISO 281:2007和ISO/TS 16281:2008。前者只考虑外部载荷对轴承寿命的影响，后者不仅考虑外部载荷对轴承寿命的影响，同时考虑滚动体与滚道的接触疲劳。风电机组主轴轴承目前均采用的是滚子轴承，对于径向滚子轴承，标准ISO/TS 16281:2008[22]规定基本额定寿命的计算方法为

(10)

其中，ns为切片数量；qkci、qkce分别为内环和外环切片的基本额定动载荷；qkei、qkee分别为内环和外环切片的当量动载荷。

标准ISO/TS 16281:2008的修正额定寿命同样采用一种系统的方法来计算疲劳寿命，其具体计算方法为

(11)

其中，eC为润滑系数；Cur为疲劳极限载荷；Pks为当量动载荷；κ为污染系数。

润滑脂添加剂对轴承的计算寿命具有很大的影响，在实际应用中很难判断并确保添加剂的应用效果，文中基于标准ISO/TS 16281:2008规定的基本额定寿命计算方法对圆柱滚子轴承进行计算。

2 主轴传动系统模型建立

风力发电机主轴传动系统具有传递轮毂一侧风载的功能，为了使主轴轴承运行更加符合实际工况，通过Romax软件对风机主轴传动系统特异性建模。

2.1 模型的建立

基于Romax软件建立某兆瓦双馈式风力发电机组主轴及轴承三维模型，默认Z轴正方向沿轴线方向从左向右，如图3所示。

图3 风电机组主轴模型

该机型主轴采用两点支撑，主轴材料为34CrNiMo6，表面处理方式选择表面硬化并抛光。前轴承是单列圆柱滚子轴承，后轴承是双列圆锥滚子轴承。以圆柱滚子轴承为主要分析对象，根据系统高级轴承模块生成需要的轴承内部参数，完成圆柱滚子轴承的定义。圆柱滚子轴承由内圈、外圈、滚动体以及保持架组成，轴承结构和材料参数见表1。

表1 圆柱滚子轴承设计参数

仿真系统采用美孚460WT润滑剂，型号为Mobil SHC 460 WT(grease)，润滑类型为脂润滑，润滑方式为自动润滑，轴承工作温度采用默认设置。圆柱滚子轴承内圈与主轴配合安装，外圈与轴承座配合安装，初始径向游隙为535 μm，模型中轴承内外圈定位预紧方式设为固定，内外圈初始轴向与径向定位预紧量为0 μm。

2.2 载荷工况的施加

轮毂侧设为输入功率，齿轮箱侧设为输出功率，由GH-Bladed软件模拟得到轮毂中心疲劳载荷数据，对主轴传动系统受力分析，建立平衡方程，将不同工况下的已知轮毂处疲劳载荷转变为轴承目标等效疲劳载荷[23]。处理后得到风机主轴轴承的部分工况数据如表2所示，前轴承圆柱滚子轴承等效载荷F1r=2.468 MN，后轴承双列圆锥滚子轴承F2a=0.685 MN，F2r=1.248 MN。主轴转速设置为9.98 r/min，工况载荷作用时长为36 s。

表2 工况数据

2.3 轴承配合制的选择

滚动轴承经常利用轴承内圈与轴之间或外圈与轴承座之间的紧密过盈配合，以防止接触界面的微动磨损，对选型确定的圆柱滚子轴承进行分析：轴承内圈与轴的配合采用基孔制，基准孔的基本偏差(下极限偏差)为零。轴承内圈与轴的配合公差带如图4a所示。轴承外圈与轴承座的配合采用基轴制，基准轴的基本偏差(上极限偏差)为零，轴承外圈与轴承座孔的配合公差带如图4b所示。

图4 轴承配合元件的配合公差带图

3 仿真结果与分析

3.1 配合公差对轴承寿命的影响

在实际工程应用过程中，部件之间的配合并不直接标注过盈量的多少，而是通过公差与配合来计算过盈量的范围[24]，配合公差的选择会对轴承装配过盈量产生影响，进而影响轴承的径向游隙，过盈量太大可导致轴承的游隙消除，甚至使轴承出现负游隙或过盈，对轴承产成较大的影响。

(a)以风速10 m/s时的载荷工况为例，分析前轴承圆柱滚子轴承，外圈平均配合过盈量设为定值，分析轴承内圈与主轴的配合公差，内圈公差等级为IT7。

轴承内圈配合采用基孔制，内圈极限尺寸范围为0～+105 μm，公差为H7，主轴配合等级与过盈量见表3，其中负值表示过盈，正值表示间隙。

表3 主轴配合等级与过盈量

不同主轴配合公差等级下的轴承寿命数据处理如图6所示。

图6 不同主轴配合公差等级的轴承寿命

从图6可知，保持轴承座公差等级不变，当主轴配合等级为a,主轴尺寸极限偏差范围为0～+66 μm时，轴承寿命值为6.546 8×105h，改变主轴配合公差等级使主轴与轴承内圈过盈量逐渐增大，轴承寿命值也不断增加。主轴配合等级为f时，轴承内圈与主轴为过盈配合，且达到最佳过盈量500.5 μm，轴承寿命值相比配合等级e升高了63.36%，具有十分显著的提高。主轴配合等级为g时，轴承寿命值急剧下降，这是由于过盈量过大得使轴承内圈周向拉应力增大，进而使得滚道次表层最大剪应力增大减小了轴承内圈寿命，过盈量太大会导致轴承更容易失效。主轴与轴承内圈的配合精度对轴承疲劳寿命具有较大的影响。

(b)以风速10 m/s时的载荷工况为例，主轴与轴承内圈平均配合过盈量设为定值，分析轴承外圈配合公差，轴承外圈公差等级为IT6。

轴承外圈的配合采用基轴制，外圈极限尺寸范围为-78～0 μm，公差为h6，轴承座配合等级与过盈量的大小见表4。

表4 轴承座配合等级与过盈量

根据不同轴承座孔配合公差计算的轴承寿命数据处理如图7所示。由图7可知，保持主轴配合公差等级不变，当轴承座的公差等级为A，轴承座尺寸极限偏差范围为+390～+515 μm时，轴承寿命值为1.570 8×106h，改变轴承座配合公差等级使得轴承座与轴承外圈的配合过盈量逐渐增大，轴承寿命值不断减小，这是因为过盈量的增大使得圆柱滚子轴承的径向游隙减小，使轴承最大滚道应力增大，寿命减小。轴承座配合公差等级为F时，轴承外圈与轴承座孔出现过盈，过盈量为23.5 μm，与配合等级E相比，轴承寿命值降低0.39%。轴承座配合公差的改变对圆柱滚子轴承的寿命影响相对较小，其原因是轴承安装于轴承座之上，外圈与轴承座内圈过盈量较小，对轴承径向游隙的影响较小。

图7 不同轴承座配合公差等级的轴承寿命

3.2 粗糙度对轴承寿命的影响

韩俊菊等[25]研究了接触面扩大、法向压力和试样与模具之间的滑动距离对微挤压过程表面粗糙度的影响。杨伟等[26]构造出符合高斯分布的表面形貌三维模型的新方法，模拟表面粗糙度对过盈配合滑动轴承性能的影响。为了研究粗糙度对轴承寿命的影响，保持轴承与主轴及轴承座的公差等级不变，在主轴及轴承座原有公差的基础上考虑粗糙度Ra值，由于安装表面存在微小的峰谷，使得主轴与轴承内圈，轴承座与轴承外圈之间的过盈量要比名义尺寸小，配合的实际过盈量的按式(12)计算。主轴及轴承座的表面粗糙度将会影响安装后的过盈量，故在基本公差配合的基础上考虑表面粗糙度的影响，即分析不同粗糙度值引起的配合过盈量变化对轴承寿命的影响。

Δd=Δs-Δh

(12)

式中，Δd为实际过盈量；Δs为名义过盈量；Δh为粗糙度。

对于前轴承圆柱滚子轴承，主轴配合等级为f，轴承座公差等级为B，以风速10 m/s的载荷工况为例，计算考虑主轴及轴承座的不同配合表面粗糙度时轴承的寿命如图8、图9所示。

图8 不同主轴粗糙度的轴承寿命

图9 不同轴承座粗糙度的轴承寿命

从图8可知，主轴表面粗糙度值的大小对轴承寿命有明显的影响，其中主轴粗糙度Ra0.8时轴承寿命最大为1.267 5×106h。随着主轴表面粗糙度值的增加，轴承寿命不断减小，粗糙度Ra12.5时轴承寿命最小，寿命值降低2.34%，降低幅度最大。主轴配合表面粗糙度值的增加对轴承寿命影响较大，因此需要提高主轴的表面加工精度。

从图9可知，轴承座表面粗糙度值的大小对轴承寿命有一定程度的影响，粗糙度Ra0.8和Ra1.6时轴承寿命值基本相同，其中主轴粗糙度Ra0.8时轴承寿命最大，为1.617 51×106h。随着粗糙度值的增加，轴承寿命值不断降低，粗糙度Ra12.5时轴承寿命最小，且降低幅度最大，与Ra6.3相比寿命值降低0.012%。圆柱滚子轴承外圈与轴承座不容易发生相对滑动，因此，采用一定的过渡或间隙配合，相比于主轴表面加工精度对轴承寿命的影响程度要小一些，建议适度降低与圆柱滚子轴承的相配合的轴承座孔的表面精度。

4 结论

基于Romax仿真平台，建立了兆瓦级风机主轴传动系统分析模型，通过研究配合尺寸精度对主轴圆柱滚子轴承承载特性及疲劳寿命的影响，得到以下结论：

(1)主轴公差配合的选择对轴承疲劳寿命具有较大的影响，主轴尺寸极限偏差范围为+520～+586 μm时，轴承有较高的寿命，主轴公差等级过大或过小均可能减小轴承寿命。轴承座配合公差的改变对圆柱滚子轴承的寿命影响相对较小。平均风速为10 m/s时的载荷工况下，按照本文方法推荐轴承与主轴极限尺寸范围优先为+520～+586 μm，与轴承座极限尺寸范围优先为+390～+515 μm。

(2)从过盈配合的角度考虑，主轴配合表面粗糙度值的增加对轴承寿命影响较大，因此需要提高主轴的表面加工精度，主轴表面最佳粗糙度值为Ra0.8，考虑到加工成本也可以选择Ra1.6。轴承座孔配合表面精度相比于主轴表面加工精度对轴承寿命的影响程度要小一些，因此可以适度降低轴承座孔配合表面的加工精度，可选Ra6.3或Ra12.5，为工程的生产实践提供一定的技术指导。

(3)主轴轴承过盈配合安装多采用热装法，利用热胀冷缩原理加热轴承，使其内圈胀大，实现准确安装，其中轴承加热工艺参数的确定对轴承的装配质量至关重要。

(4)从数值计算的角度对配合表面的精度进行模拟分析，研究结论可以为轴承承载评估和寿命预测提供参考。因为缺乏考虑充分模拟实际配合表面的多重耦合因素影响，存在一定的局限性。