旋转惯性调谐质量阻尼器对风电塔的减振研究
2021-12-24朱大壮熊世树
朱大壮,熊世树
(华中科技大学土木与水利工程学院,武汉430074)
1 引言
进入21世纪以来,风能作为一种可再生、无污染的清洁能源逐步进入大众视野,在发电领域也获得了迅速的发展。截至2018年,国内的风力发电量占比4.79%,仅次于火力和水力发电,累积风电装机量同比增长16.6%,保持较好的发展势头。
风力发电塔作为长周期柔性结构,对风荷载较为敏感,风振响应较大,以至于影响机舱内系统的正常工作。因此,如何降低风振响应引起了学界内的广泛关注。目前,减振研究的重点在应用消能减振装置与调频减振装置上。黄超[1]提出了一种“自适应减振装置”,通过实验证明了该装置在抑制振动方面具有较好的效果。Asai T等[2]提出了一种换能器——调谐惯性质量电磁换能器(TIMET)。该换能器可以通过调节参数来降低结构的振动,同时将振动能量转换为电能。张自立等[3]研制出了圆球减振装置,包括金属圆球、底座、上部盖板与黏弹性摩擦层4部分。当结构振动时,金属圆球反向运动并通过摩擦消耗振动能量。刘文峰等[4]研究了调谐液体柱形阻尼器(TLCD)动力系统的形态演化,提出了基于结构可靠度的参数优化设计方法,采用有限元一体化模型研究了地震作用下海上风力发电高塔系统的随机最优控制。
本文提出一种降低风振响应的调频减振装置——旋转惯性调谐质量阻尼器(RITMD)。RITMD一方面可以通过较小的附加质量来获得较大的惯性质量,提升TMD系统的性能;另一方面可以通过电磁感应产生电流,消耗振动能量[5]。本文建立六自由度简化模型模拟风电塔,对比分析了在风载作用下无控制结构、TMD控制与RITMD控制结构的动力响应。
2 旋转惯性调谐质量阻尼器
2.1 RI TMD结构
RITMD由质量块、弹簧、黏滞阻尼器以及电磁惯性阻尼器组成。核心部件为电磁惯性阻尼器,具体构造如图1所示。图1中md为质量块,b为电磁惯性阻尼器,kd为弹簧,cd为黏滞阻尼器。当风力发电塔受到风荷载而发生振动时,RITMD通过电磁感应与摩擦消耗一部分振动能量,从而降低结构的动力响应。

图1 RI TMD与电磁惯性阻尼器结构图
2.2 电磁惯性阻尼器阻尼力计算
电磁惯性阻尼器产生的阻尼力可分为2部分:一是惯性轮旋转产生的惯性力;二是因电磁感应产生的电磁力。
2.2.1 惯性部分
当图1中的螺杆轴向运动时,忽略摩擦阻力,根据Lazar IF等[6]的研究结果,惯性力Fi的计算式为:
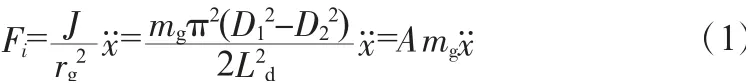
式中,J为惯性轮的转动惯量;rg为小齿轮的半径;mg为惯性轮的质量;D1为惯性轮的外径;D2为惯性轮的内径;x..为螺杆轴向运动加速度;Ld为螺杆导程。定义为惯性质量放大系数,μ=D2/D1为惯性轮内径与外径之比,B=D1/Ld为惯性轮外径与螺杆导程之比。通过改变μ与B2个参数的值就可以设计出具有较大放大倍数的惯性阻尼器。外径与导程之比不变,减小圆环内径与外径之比,或者是内径与外径之比不变,增大外径与导程之比,都可以显著的增加惯性质量的放大倍数。
2.2.2 电磁部分
电磁阻尼器由永磁体和定子线圈组成,径向布置,采用三相绕组的方式,电磁力的计算公式为:

式中,Pe为电磁耗能功率;cr为等效阻尼;x·为螺杆运动轴向速度。负载为三相绕组,得到Pe的计算公式如下:

式中,Ra为线圈电阻;R为负载电阻;E0为一相电动势;Xs为同步电抗。
3 建立RI TMD系统的运动方程
3.1 风电塔六质点简化模型
以某1.5 MW级的风力发电塔为原型,该塔轮毂中心高度77.8 m,风轮直径75 m,塔底直径4.5 m,厚度50 mm,塔顶直径3.08 m,厚度20 mm,在离地15 m范围内塔筒的截面不变,在15~75 m范围内截面均匀渐变。机舱高5.6 m,质量80 t,叶片与轮毂的质量之和为68 t,上部结构的总质量148.5 t。塔架采用钢结构,总质量139.7 t。
将风电塔简化为六自由度集中质点模型,考虑顺风向的自由度,取上下塔段各一半质量组成集中质点的质量。另外,第6质点的质量由叶片、轮毂和机舱累加得到。
将整个风电塔模型视为悬臂梁,通过柔度法求得结构的柔度矩阵,其逆矩阵就是简化模型的刚度矩阵。
3.2 运动方程
整体运动方程可写为:

安装RITMD后结构增加了一个自由度,相应的质量矩阵可写为:

3.3 风荷载的模拟
运用线型滤波法中的AR法,选取Davenport谱,通过MATLAB自编程序生成作用在集中质点上的脉动风速时程。取离地10 m处的平均风速,地面粗糙度系数k=0.005。图2为模拟功率谱与目标功率谱的比较。
如图2所示,AR法得到的脉动风速均值大致为零,同时样本谱线趋势与目标谱线比较接近,说明该方法获得的脉动风速时程较为可靠。

图2 模拟功率谱与目标谱的对比
4 RI TMD减振效果分析
4.1 控制系统的具体参数
根据Hartog D和Pieter J[7]的研究,TMD结构的最优阻尼比和频率比分别为:
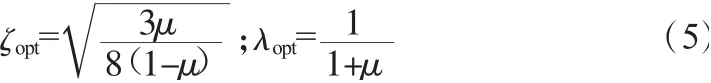
式中,ζopt为TMD的最优阻尼比,μ为TMD与主结构的质量比,λopt为最优频率比。
对TMD结构,取mTMD=8 000 kg,质量比约为2%,已知风电塔结构的一阶自振频率为0.493 Hz,计算得到:
kTMD=60 000 N/m,cTMD=5 000 N·s/m
式中,kTMD为TMD系统的刚度;kTMD为TMD系统的阻尼。
对于相同质量的RITMD,核心采取查道锋[8]设计的电磁惯性阻尼器并加以改进,质量800 kg,等效惯性质量b为100 000 kg,等效阻尼cr为27 315 N·m/s。mTMD取7 200 kg,kTMD与cTMD的值不变。
4.2 风振控制效果
在离地10 m处的平均风速ν10=30 m/s的工况下,3种控制结构在风载作用下的塔顶位移、塔顶加速度、塔底剪力和塔底弯矩如图3所示。可以看出,在RITMD作用下,风电塔的动力响应显著降低,具体控制效果见表1,其中最大塔顶位移、最大塔底剪力和最大塔底弯矩的降低率接近30%,最大塔顶加速度的降低效果最为明显,达到了47.3%,从而得到RITMD降低风振响应的效果显著优于TMD。
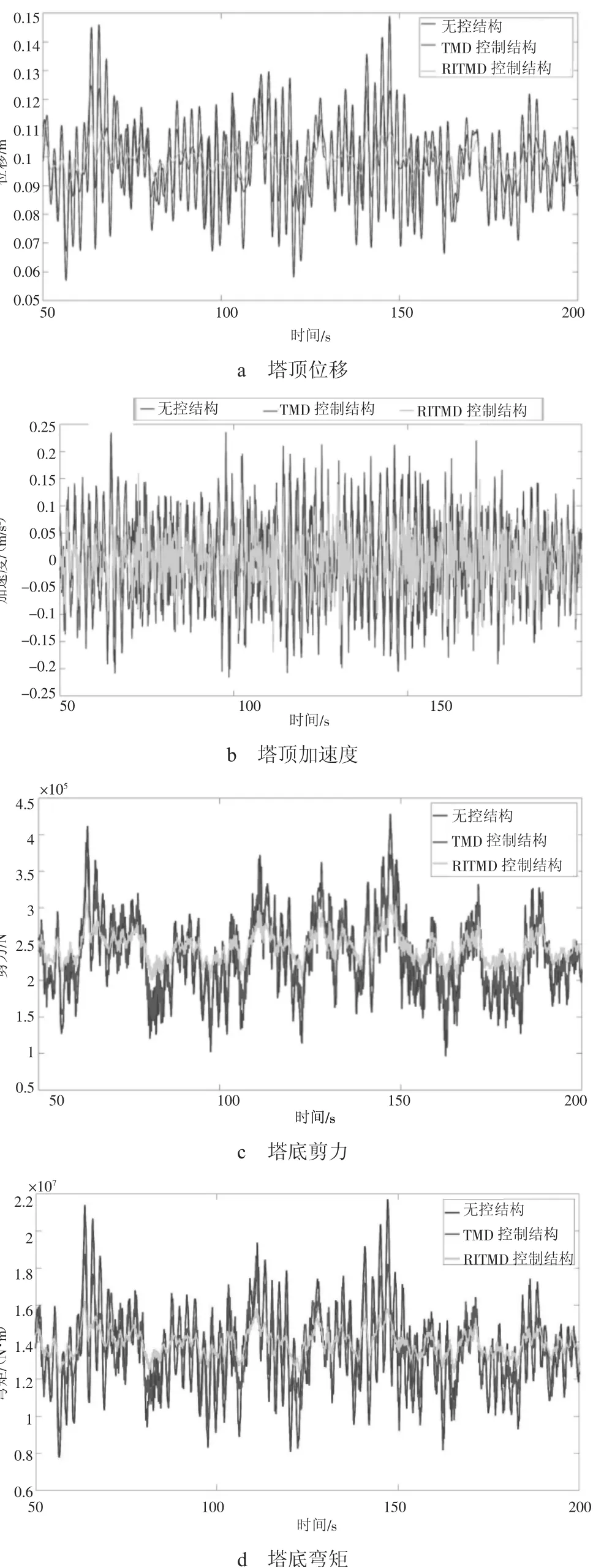
图3 3种控制系统的风振响应
保持TMD的质量不变,不断减小RITMD质量直到两者的控制效果基本一致,此时的RITMD质量为2 600 kg。结果显示,对于RITMD,仅需1/3倍TMD的质量就可以达到相同的控制效果。

表1 2种控制结构降低响应的效率
5 结论
1)本文介绍了旋转惯性调谐质量阻尼器,核心为电磁惯性阻尼器,是速度相关型阻尼器与加速度相关型阻尼器的结合。
2)建立了六自由度风电塔简化模型和RITMD风力发电塔控制运动方程,采用MATLAB自编程序,证明了RITMD在降低风电塔风振响应方面显著优于TMD,仅需1/3倍TMD的质量就可达到相同的控制效果。
